"Элементарные функции, содержащие знак модуля"

Для построения графиков функций, содержащих знак модуля, как и при решении уравнений, сначала находят корни выражений, стоящих под знаком модуля. В результате ось Ох разбивается на промежутки. Убираем знаки модуля, беря каждое выражение в каждом промежутке с определённым знаком, которые находим методом интервалов. В каждом промежутке получается функция без знака модуля. Строим график каждой функции в каждом промежутке.  В простейшем случае, когда только одно выражение стоит под знаком модуля и нет других слагаемых без знака модуля, можно построить график функции, опустив знак модуля, и затем часть графика, расположенную в области отрицательных значений y, отобразить относительно оси Ох.

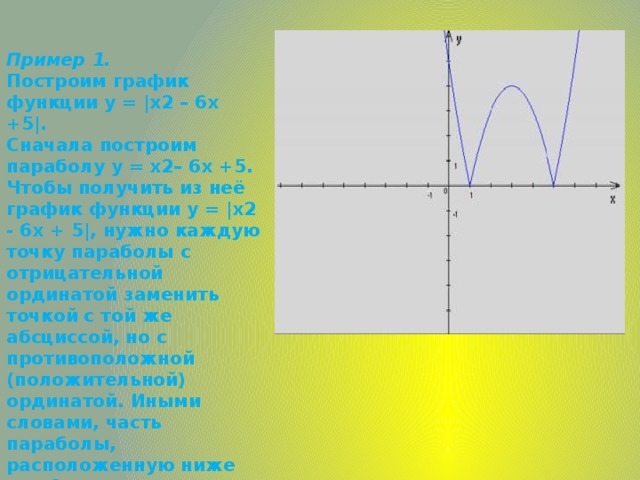
Пример 1. Построим график функции у = |х2 – 6х +5|.  Сначала построим параболу у = х2– 6х +5. Чтобы получить из неё график функции у = |х2 - 6х + 5|, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох.

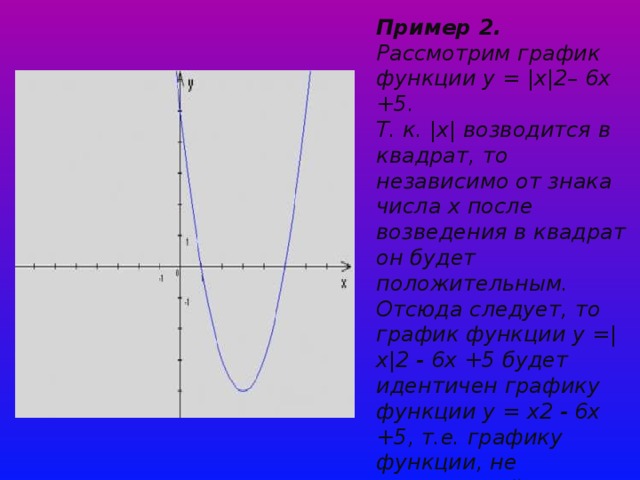
Пример 2. Рассмотрим график функции у = |х|2– 6х +5.  Т. к. |х| возводится в квадрат, то независимо от знака числа х после возведения в квадрат он будет положительным. Отсюда следует, то график функции у =|х|2 - 6х +5 будет идентичен графику функции у = х2 - 6х +5, т.е. графику функции, не содержащей знака абсолютной величины.

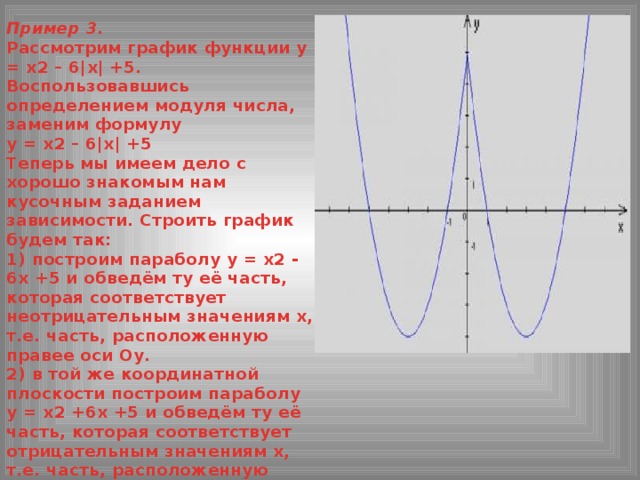
Пример 3. Рассмотрим график функции у = х2 – 6|х| +5.  Воспользовавшись определением модуля числа, заменим формулу   у = х2 – 6|х| +5  Теперь мы имеем дело с хорошо знакомым нам кусочным заданием зависимости. Строить график будем так:  1) построим параболу у = х2 - 6х +5 и обведём ту её часть, которая соответствует неотрицательным значениям х, т.е. часть, расположенную правее оси Оу. 2) в той же координатной плоскости построим параболу у = х2 +6х +5 и обведём ту её часть, которая соответствует отрицательным значениям х, т.е. часть, расположенную левее оси Оу. Обведённые части парабол вместе образуют график функции у = х2 - 6|х| +5

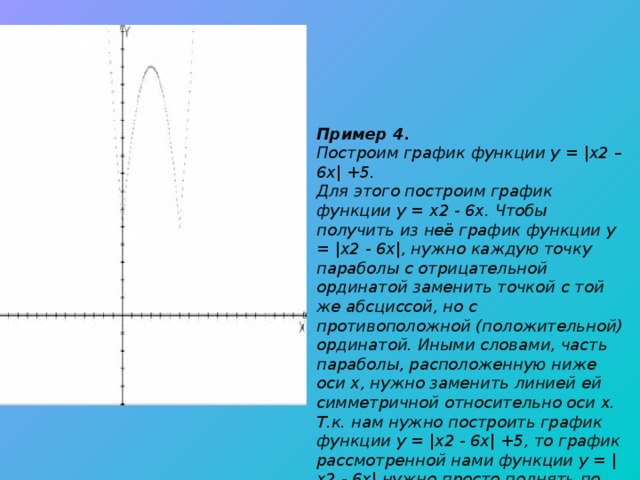
Пример 4.

Построим график функции у = |х2 – 6х| +5.  Для этого построим график функции у = х2 - 6х. Чтобы получить из неё график функции у = |х2 - 6х|, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси х, нужно заменить линией ей симметричной относительно оси х. Т.к. нам нужно построить график функции у = |х2 - 6х| +5, то график рассмотренной нами функции у = |х2 - 6х| нужно просто поднять по оси у на 5 единиц вверх .

Пример 5.

Построим график функции у = х2 - |6х+5|. Для этого воспользуемся хорошо нам известной кусочной функцией. Найдём нули функции 

у = 6х +5 6х + 5 = 0 при . Рассмотрим два случая: 1)Если х0, то уравнение принимает вид у = х2+ 6х +5. Постоим эту параболу и обведём ту её часть, которая расположена левее точки с координатами.

Пример 6 . Построим график функции у = |х2 – 6|х| +5|.  Для этого мы построим график функции у =х2- 6|х| +5. Построение этого графика мы проводили в примере 3. Т. к. наша функция полностью находится под знаком модуля, то для того, чтобы построить график функции у = |х2 – 6|х| +5|, нужно каждую точку графика функции у = х2 – 6|х|+5 с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой, т.е. часть параболы, расположенную ниже оси Ох, нужно заменить линией ей симметричной относительно оси Ох

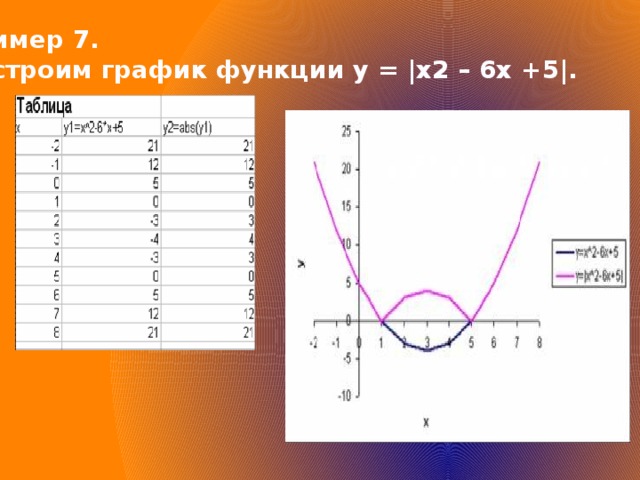
Пример 7.

Построим график функции у = |х2 – 6х +5|. 

Когда в «стандартные» уравнения прямых, парабол, гипербол включают знак модуля, их графики становятся необычными и даже красивыми.