Элементы алгебры логики

Элементы алгебры логики

Формы мышления

Логика — наука, изучающая законы и формы мышления.

Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления.

Основными формами абстрактного мышления являются понятия, высказывания (суждения) и умозаключения.

Понятие — форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов. Понятия в языке выражаются словами.

Высказывание — это форма мышления, в которой что-либо утверждается или отрицается о предметах, признаках или их отношениях.

Умозаключение — форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, мы по определенным правилам вывода получаем суждение-заключение.

Алгебра логики (высказываний)

                Высказывание — это любое предложение какого-либо языка (утверждение), содержание которого можно определить как истинное или ложное.

      Всякое высказывание или истинно, или ложно; быть одновременно и тем и другим оно не может.

Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:

А = {Аристотель - основоположник логики}

В = {На яблонях растут бананы}.

       Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А  = 1, В = 0.

Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание.

10. Сканер — это устройство, которое может напечатать на бумаге то, что изображено на экране компьютера. Сумма чисел 2 и 6 больше числа 8. Мышь — устройство ввода информации. " width="640"

Задания 1, 2

1. Объясните, почему следующие предложения не являются высказываниями:

1) Какого цвета этот дом?

2) Число Х не превосходит единицы.

3) 4Х+3

4) Посмотрите в окно.

5) Пейте томатный сок!

6) Вы были в театре?

7) Сумма числа 5 и Х равна 10.

2 . Какие из следующих предложений являются истинными, а какие ложными высказываниями?

Город Париж — столица Франции.

Число 2 является делителем числа 7.

3 + 5 = 2 * 4.

2 + 6 10.

Сканер — это устройство, которое может напечатать на бумаге то, что изображено на экране компьютера.

Сумма чисел 2 и 6 больше числа 8.

Мышь — устройство ввода информации.

Основные операции алгебры логики

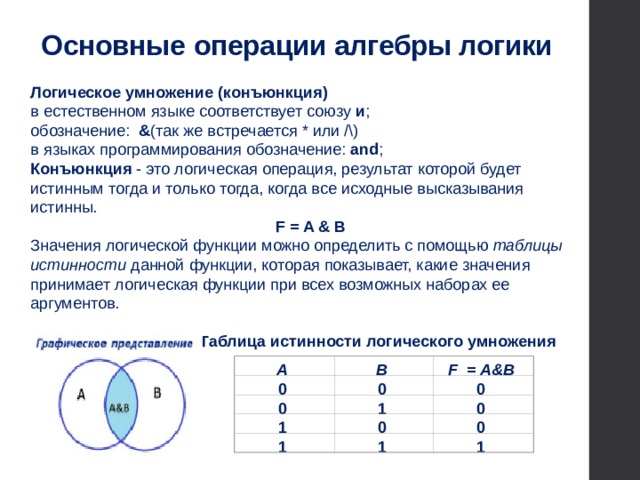
Логическое умножение (конъюнкция)

в естественном языке соответствует союзу и ;

обозначение: & (так же встречается * или /\)

в языках программирования обозначение: and ;

Конъюнкция - это логическая операция, результат которой будет истинным тогда и только тогда, когда все исходные высказывания истинны.

F = A & B

Значения логической функции можно определить с помощью таблицы истинности данной функции, которая показывает, какие значения принимает логическая функции при всех возможных наборах ее аргументов.

Таблица истинности логического умножения

В

F = А&В

А

0

0

0

0

0

1

1

0

0

1

1

1

Основные операции алгебры логики

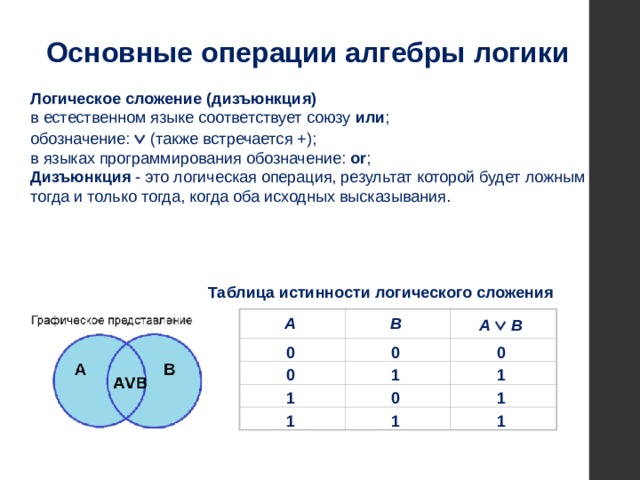
Логическое сложение (дизъюнкция) в естественном языке соответствует союзу или ;

обозначение: Ú (также встречается +);

в языках программирования обозначение: or ;

Дизъюнкция - это логическая операция, результат которой будет ложным тогда и только тогда, когда оба исходных высказывания.

Таблица истинности логического сложения

А Ú В

В

А

0

0

0

0

1

1

0

1

1

1

1

1

Основные операции алгебры логики

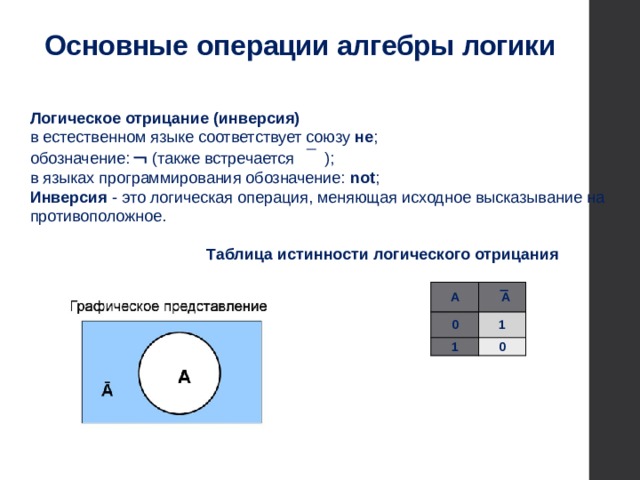
Логическое отрицание (инверсия) в естественном языке соответствует союзу не ;

обозначение:  (также встречается  );

в языках программирования обозначение: not ;

Инверсия - это логическая операция, меняющая исходное высказывание на противоположное.

Таблица истинности логического отрицания

A

0

 A

1

1

0

8 ) или (X )) примет значение: а) ложь; б) истина. " width="640"

Задания 3-5

3 . Среди следующих высказываний укажите составные; выделите в них простые, обозначив каждое их них буквой; запишите с помощью логических операций каждое составное высказывание.

1) Число 376 четное и трехзначное.

2) Неверно, что Солнце движется вокруг Земли.

3) Земля имеет форму шара.

4) На уроке математики старшеклассники отвечали на вопросы учителя и писали самостоятельную работу.

4. Найдите значения логических выражений:

    а) (1 Ú 1) Ú (1 Ú 0);

    б) ((1 Ú 0) Ú 1) Ú 1;

    в) (0 Ú 1) Ú (1 Ú 0);

    г) (0&1)&1;

5 . При каких значениях числа X логическое выражение не (( X 8 ) или (X )) примет значение:

а) ложь;

б) истина.

Задания 6,7

6. Определите истинность простых высказываний:

А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

7. На основе результатов задания №6 определите истинность составных высказываний:

а) (А /\ В) /\ (C Ú D); б) (А /\ В) \/ (C Ú D);

Логические выражения и таблицы истинности

Логические операции имеют следующий приоритет: действия в скобках,  , &, Ú

Алгоритм построения таблицы истинности:

1. Подсчитать количество переменных n в логическом выражении.

2. Определить число строк в таблице m = 2 n .

3. Подсчитать количество логических операций в формуле.

4. Установить последовательность выполнения логических операций с учетом скобок и приоритетов.

5. Определить количество столбцов в таблице: число переменных плюс число операций.

6. Выписать наборы входных переменных.

7. Провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной последовательностью.