Явления переноса обусловлены столкновениями молекул. Количественные характеристики этих явлений зависят от средней длины свободного пробега молекул. В связи с этим интересно рассмотреть явления переноса в условиях отсутствия столкновений между молекулами. Такие условия легко получить. Известно, что λ ~ 1/p, следовательно, при уменьшении давления, при некотором p, λ может сравняться с размерами сосуда с газом.
Такое состояние газа, при котором средняя длина свободного пробега молекул становится больше размеров сосуда с газом, называется вакуумом. В широком смысле этого слова вакуумом называется состояние газа, при котором его плотность меньше, чем при нормальных условиях.
Различают низкий, средний и высокий вакуум. Низкий вакуум состояние газа, при котором λ несколько меньше размеров сосуда с газом. Средний вакуум – λ сравнима с размерами сосуда с газом. Высокий вакуум – λзначительно больше размеров сосуда с газом.
Понятие вакуума – понятие относительное. Чем меньше размеры сосуда с газом, тем при больших давлениях в нем создаются условие вакуума. Для газа, который находится в пористом веществе, с размерами пор ~ 10-5см атмосферное давление уже является вакуумом.
Явления переноса в газах, обусловленные столкновениями молекул (диффузия, вязкость, теплопроводность), в вакууме будут протекать иначе, чем при атмосферном давлении. Те явления, которые не зависят от столкновений между молекулами, протекают одинаково как в вакууме, так и при больших давлениях. Основное уравнение МКТ газов получено при рассматривании взаимодействия молекул со стенками сосуда с газом. Поэтому это уравнение и вытекающие из него газовые законы справедливы и при очень малых давлениях.
Рассмотрим явления переноса в вакууме. В случае среднего и высокого вакуума имеет место не теплопроводность, а теплопередача, которая наблюдается, если стенки сосуда с газом нагреты до разных температур. После столкновения со стенкой сосуда молекула отражается, приобретая кинетическую энергию, соответствующую температуре стенки. После столкновения с более горячей стенкой молекулы без столкновений между собой достигают холодной стенки и при соударении передают ей часть своей энергии. Отражаясь от холодной стенки, они обладают энергией соответствующей температуре этой стенки и т.д.
Внутреннее трение (вязкость) как таковое в вакууме теряет свой смысл. Однако если в вакууме движется тело, то из-за столкновений с молекулами газа на него будут действовать силы трения.
В вакууме перенос энергии или импульса осуществляется не путем передачи от молекулы к молекуле, а за счет столкновения молекул со стенками сосуда или с движущимся телом.
Теплопередача будет наблюдаться, в случае, когда стенки сосуда имеют разные температуры. Если две пластины двигаются в вакууме с разными скоростями, наблюдается проявление вязкости (рис.1).


Рис.1 Теплопередача и вязкость газов в условиях вакуума
Пусть λ >> h. В условиях вакуума (молекулы не сталкиваются между собой) градиент температуры заменяется величиной  ,
,
а градиент скорости величиной .
.
Средняя длина свободного пробега молекул заменяется величиной h. С учетом этого закон Фурье для теплопроводности и закон Ньютона для силы трения принимают вид:
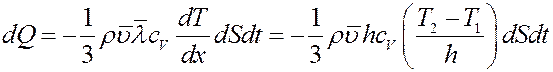 (1)
(1)
 (2)
(2)
Из (1) и (2) коэффициенты теплопроводности и вязкости соответственно равны  (3)
(3)
 (4)
(4)
Из (3) и (4) видно, что в отличие от нормальных условий, в условиях вакуума χ и η зависят от давления газа (пропорциональны плотности, а значит и давлению газа).
Согласно (1) количество переносимого тепла может сильно уменьшиться при понижении давления газа. Очень малая теплопроводность разряженного газа используется в сосудах Дьюара (рис.3).

Рис.3 Сосуд Дьюара
1 - внутренняя оболочка, 2 - внешняя оболочка, 3 - вакуумная изоляция, 4 - горловина с низкой теплопроводностью, 5 - отросток для откачки
Сосуд Дьюара имеет двойные стенки цилиндрической или сферической формы. Газ между стенками откачан до очень низких давлений. Для уменьшения передачи тепла излучением на внутреннюю и наружную стенки наносится зеркальное покрытие. Теплопроводность разряженного газа в десятки раз меньше теплопроводности газа при нормальном давлении. Сосуды Дьюара используют для хранения низкотемпературных кипящих жидкостей (сжиженные газы), а так же для хранения горячих жидкостей (термос).
Течение газа в условиях вакуума происходит иначе, чем при давлениях сравнимых с атмосферным. Течение газа при отсутствии столкновений между молекулами называется молекулярным течением, а процесс истечения разреженного газа из отверстия, характерные размеры которого много меньше длины свободного пробега, называется молекулярной эффузией или просто эффузией.
Рассмотрим заполненный разреженным газом сосуд, разделенный перегородкой с небольшим отверстием диаметром d. Будем считать, что размер отверстия и толщина перегородки много меньше длины свободного пробега молекул газа (рис.4).
 Рис.4. Эффузия газов
Рис.4. Эффузия газов
Пусть в одной половине сосуда концентрация молекул n1, давление p1, температура T1, а в другом n2, p2, T2 соответственно. При нормальных давлениях λ << d и равновесие в сосуде будет наблюдаться при одинаковых давлениях: p1 = p2, или n1kT1 = n2kT2. Отсюда следует: 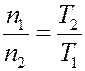 (5)
(5)
Из (5) видно, что концентрация молекул, а, следовательно, плотность газа обратно пропорциональна температуре.
Для вакуума λ >> d и молекулы не сталкиваются между собой. Поэтому равновесие будет наблюдаться в том случае, когда число молекул проходящих через отверстие с одной стороны, за какое-то время, будет равно числу молекул проходящих через отверстие с другой стороны за это же время.
При эффузии число молекул проходящих через отверстие слева направо за время Δt будет равно:
 (6)
(6)
где: 
площадь отверстия. За это же время справа налево через отверстие пройдет N2 молекул:  (7)
(7)
При равновесии: 
Отсюда следует  (8)
(8)
Так как 
из (8) получим:  (9).
(9).
Для соотношения давлений с учетом (9) получим: 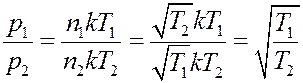 (10)
(10)
Таким образом, в отличие от нормальных условий, когда равновесие наблюдается при равенстве давлений в сосудах, в вакууме в сосудах установятся разные давления. Причем большее давление будет в сосуде с большей температурой.
Если в сосудах температуры и давления одинаковые, а газы разные (µ1 и µ2), то через отверстие будут протекать встречные эффузионные потоки. Из (6) и (7) получим:
 (11)
(11)
Известно, что: 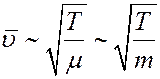
где, µ - молярная масса, m – масса молекулы. С учетом этого из (11) получим:
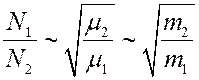 (12)
(12)
Из (12) видно, что количество газа, протекающего через отверстие обратно пропорционально  . На этом основан способ разделения газовых смесей, в частности изотопов, которые нельзя разделить химическими методами.
. На этом основан способ разделения газовых смесей, в частности изотопов, которые нельзя разделить химическими методами.
Поток газовой смеси делится на две части, одна из которых проходит через пористую перегородку (рис.5).

Рис. 5. Схема установки для разделения газовой смеси.
При прохождении газом пористого вещества наблюдается эффузия, так как λ значительно больше размеров пор. Поэтому, согласно (12), поток 2 после прохождения через перегородку будет обогащен легкими молекулами по сравнению с потоком 1. В потоке 3 легких молекул больше чем в потоке 2 и т.д. В результате поток 4 содержит в основном более легкий изотоп.
Получение вакуума необходимо как в лабораторных условиях для опытов, так и в промышленности.
Две основные задачи вакуумной техники: 1) получение высокого вакуума, 2) измерение низких и сверхнизких давлений.
Удаление воздуха из сосуда осуществляется воздушными насосами. Насос с приспособлениями (соединительные трубки, краны, манометры) называется вакуумной установкой. Воздух, который откачивается из сосуда, выбрасывается в атмосферу. При этом насос преодолевает внешнее давление атмосферы, которое называется противодавлением. Чем выше вакуум, который надо получить, тем ниже должно быть противодавление выхлопу насоса. Не существует таких насосов, которые могли бы откачивать газ до давлений 10-5 – 10-6мм.рт.ст. и выбрасывать откачанный газ в атмосферу (противодавление 760 мм.рт.ст.). Поэтому для создания низкого противодавления используют предварительные, так называемые форвакуумные насосы. Их соединяют последовательно с насосами, создающими высокий вакуум. Эти насосы могут выталкивать откачанный газ только в пространство с пониженным (меньше атмосферного) давлением. Такие насосы называются высоковакуумными, и они могут работать только совместно с форвакуумными насосами.
В качестве форвакуумных насосов часто используются ротационные масляные насосы (рис.6).

Рис.6 Схема ротационного масляного насоса

Рис.7 Пояснение принципа работы ротационного масляного насоса
Насос состоит из полого металлического цилиндра 1, внутри которого эксцентрично вращается второй цилиндр – ротор – 2, верхняя часть которого прилегает к внутренней поверхности цилиндра 1. В прорезь ротора входят две пластины – лопасти – 3, которые прижимаются пружиной 4 к внутренней поверхности цилиндра 1. При вращении ротора, после того как одна из пластин (А рис.7а) проходит всасывающую трубку 5 воздух из откачиваемого сосуда поступает в полость насоса 6, где давление газа меньше из-за постоянного увеличения объема между лопастью и трубкой 5 (рис.6, 7б). Когда трубку 5 пройдет следующая пластина (В рис.7в) объем 6 отсекается от откачиваемого сосуда (рис.6, 7в) и при дальнейшем движении ротора газ в полости 6 сжимается пластиной В и выталкивается из насоса через выпускной (обратный) клапан 7 (рис.6, 7г), препятствующий поступлению газа обратно в насос. Для лучшей герметичности и смазки насоса он помещается в кожух, наполненный маслом. Лучшие форвакуумные насосы создают вакуум ~ 10-3мм.рт.ст.
Для получения высокого вакуума используются диффузионно-конденсационные, пароструйные ртутные и масляные насосы (рис.8).


Рис. 8. Схема и принцип работы ртутного пароструйного насоса
При нагревании сосуда с ртутью (органическим маслом) - 1 электрическим нагревателем 2, ртутные пары с большой скоростью выбрасываются через сопло 3 в полость насоса 4, которая охлаждается проточной водой 5. Насос соединяется с откачиваемым объемом через патрубок 6. Перед включением нагревателя в системе форвакуумным насосом создается вакуум ~10-3мм.рт.ст. Молекулы откачиваемого газа диффундируют в струю паров ртути (масла) и захватываются ей в нижнюю часть полости 4. Ртутные (масляные) пары в нижней части полости конденсируются, а молекулы газа откачиваются форвакуумным насосом через патрубок 7. Сконденсировавшаяся ртуть (масло) поступает обратно в резервуар с ртутью. В настоящее время вместо ртути в подобных насосах используют специальные органические масла с очень низким давлением насыщенных паров при комнатных температурах. Лучшие диффузионные насосы позволяют получить вакуум порядка ~ 10-9 – 10-11 мм.рт.ст.
Измерение вакуума одна из задач вакуумной техники. Манометры для измерения низких давлений называются вакуумметрами. Для измерения давлений от 760 до 0,1 мм.рт.ст. используют жидкостные U – образные манометры. Для измерения давлений от 0,1 до 10-6мм.рт.ст. используется манометр Мак-Леода, действие которого основано на законе Бойля-Мариотта (рис.9).

Рис.9 Манометр Мак-Леода
Перед началом измерений сосуд 1 опускают так, чтобы уровень ртути в сосуде 2 стал ниже уровня 6. При этом манометр через трубку 5 соединяется с сосудом, в котором измеряется давление. При подъеме сосуда 1 ртуть поднимается выше уровня 6 и отсоединяет сосуд 2 и капилляр 3 от сосуда, в котором измеряется давление. Сосуд 1 поднимают до тех пор, пока ртуть в капилляре не дойдет до определенной метки. Если объем сосуда 2 с частью капилляра до метки равен V, а объем части капилляра от метки до верхнего конца – ΔV, то газ, давление которого было p, (измеряемое давление) сожмется в капилляре 3 до давления p1. Согласно закону Бойля-Мариотта:

Тогда:

Так как V >> ΔV, то:

где p1 – давление сжатого газа в капилляре объемом ΔV. Величина давления p1 находится по разности уровней в капиллярах 3 и 4. Величины V и ΔVпостоянные, указанные в паспорте прибора.
Для измерения очень низких давлений используются ионизационные манометры, манометры Пирани и т.д. Манометр Пирани представляет собой стеклянную колбу, в которой натянута платиновая проволока, нагреваемая электрическим током. Колба имеет отросток для соединения с откачиваемым объемом. Коэффициент теплопроводности разряженных газов пропорционален давлению, поэтому, чем выше давление газа в колбе тем, больше его теплопроводность и ниже температура проволоки, а, следовательно, меньше ее сопротивление. По величине сопротивления можно определить давление газа. Манометры Пирани необходимо градуировать.

Рис.10 Схема включения манометра Пирани
Основы термодинамики
Лекция 10
Термодинамическая система (ТДС). Параметры состояния. Термодинамическое равновесие. Внутренняя энергия. Взаимодействие ТДС. Работа и теплота как форма обмена энергиями между ТДС. Равновесные и неравновесные процессы. Функции состояния и функции процесса.
Термодинамика это наука, которая изучает взаимосвязь между всеми видами энергии и влияние этой связи на свойства физических тел (систем). Особое положение термодинамики в физике связано с тем, что любая форма энергии при ее превращениях, в конце концов, переходит в энергию тепловых движений.
Термодинамика основана на двух основных законах, которые называются началами термодинамики.
Сформулируем одно из многих определений этих начал.
Первое начало термодинамики: невозможно возникновение или уничтожение энергии.
Второе начало термодинамики: невозможен процесс единственным результатом, которого было бы превращение теплоты в работу.
Американский физик Чарльз Сноу на примере 2-го начала термодинамики в книге «Две культуры» демонстрирует разрыв в культурном отношении между специалистами и неспециалистами в области естественных наук: «… и те и другие могут обсуждать произведения Шекспира, но, как только спор коснется соответствующих аспектов II-го начала термодинамики, дискуссию могут продолжать только те, кто имеет естественно-научное образование».
Чтобы было очевидно значение этих законов для науки и техники их можно сформулировать иначе. Для этого надо ввести понятие о вечном двигателе.
Двигатель, повторяющий один и тот же процесс и способный производить (выполнять) работу большую, чем полученная им энергия называется вечным двигателем первого рода.
Тепловой двигатель, повторяющий один и тот же процесс и способный целиком преобразовать в работу всю теплоту, которую он получает от других тел, называется вечным двигателем второго рода.
Было сделано множество попыток сконструировать вечный двигатель, но ни одна из них не удалась. Объяснение этому дают два начала термодинамики.
I начало: вечный двигатель первого рода не возможен.
II начало: вечный двигатель второго рода не возможен.

Рис.1 Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η > 1.

Рис.2 Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – «вечный двигатель второго рода»; 2 – самопроизвольный переход тепла от холодного тела к более теплому («идеальная холодильная машина»).
Согласно вышесказанному наибольший практический интерес представляет преобразование тепловой энергии в механическую и наоборот. Однако прежде чем рассматривать эти вопросы необходимо рассмотреть термодинамическую систему, параметры ее состояния, виды процессов и т.д.
Термодинамическая система (ТДС) - это совокупность макроскопических тел, которые могут взаимодействовать между собой и с другими телами (внешней средой) - обмениваться с ними энергией и веществом. В частности, термодинамическая система может состоять из одногомакроскопического тела.
Физические величины, которые характеризуют состояние ТДС, называются термодинамическими параметрами состояния или просто параметрами состояния. Обычно в качестве параметров состояния выбирают объем V, который занимает масса вещества m, давление p и температуру T. Эти параметры не независимые. Они связаны уравнением состояния.
Самая простая ТДС – газ, который характеризуется параметрами p,V,T. Более сложная ТДС – двухфазная – жидкость, которая находится в равновесии с насыщенным паром.
ТДС могут быть частично или полностью изолированными. Если ТДС находится в теплонепроницаемой (адиабатной) оболочке она изолирована в тепловом отношении. При этом она может быть не изолирована в механическом отношении (перемещение поршня в теплоизолированном цилиндре). Если ТДС ни каким образом не взаимодействует с окружающей средой, то она полностью изолированная (замкнутая).
Система находится в термодинамическом равновесии, если макроскопические параметры, характеризующие ее состояние, остаются постоянными сколь угодно долго. Очевидно, что в состоянии равновесия не могут протекать такие процессы как диффузия, теплопередача, фазовые переходы, химические реакции и т.д.
Опыты показывают, что если параметры состояния в разных точках системы не одинаковые – нет состояния равновесия, то с течением времени система сама по себе перейдет в состояние равновесия. Процесс перехода термодинамической системы из неравновесного состояния в равновесное называется процессом релаксации, он характеризуется временем релаксации. Термодинамическое равновесие отличается от механического тем, что при неизменных макроскопических параметрах, характеризующих состояние системы, микроскопические величины – скорости, импульсы, энергия молекул беспрерывно изменяются. Тот факт, что система при этом остается в состоянии равновесия, обусловлен огромным количеством молекул.
Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p,V) в виде некоторой линии, каждая точка которой представляет равновесное состояние.









 ,
, .
.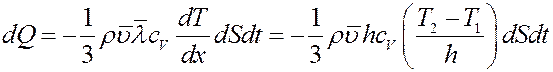 (1)
(1) (2)
(2) (3)
(3) (4)
(4)
 Рис.4. Эффузия газов
Рис.4. Эффузия газов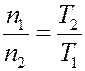 (5)
(5) (6)
(6)
 (7)
(7)
 (8)
(8)
 (9).
(9).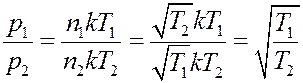 (10)
(10) (11)
(11)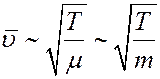
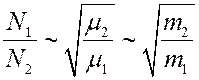 (12)
(12) . На этом основан способ разделения газовых смесей, в частности изотопов, которые нельзя разделить химическими методами.
. На этом основан способ разделения газовых смесей, в частности изотопов, которые нельзя разделить химическими методами.





















