Формула Эйлера при решении геометрических задач

Формула Эйлера при решении геометрических задач

Цели и задачи:

• познакомить обучающихся с формулой Эйлера и вывести её;
• научить обучающихся использовать формулу Эйлера при решении задач.

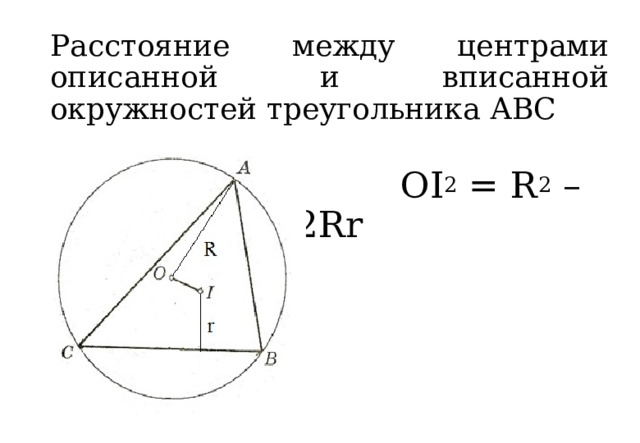
Расстояние между центрами описанной и вписанной окружностей треугольника АВС

OI 2 = R 2 – 2Rr

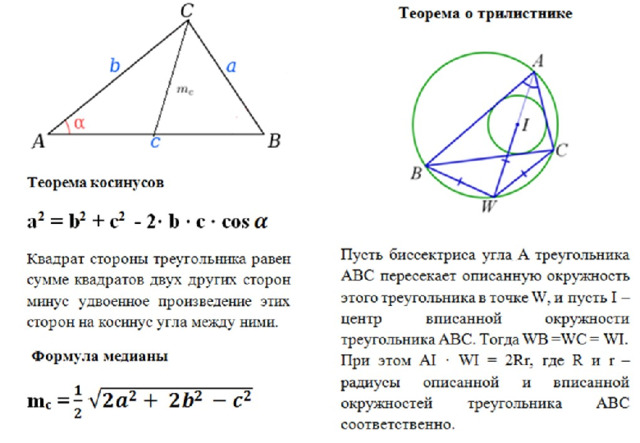
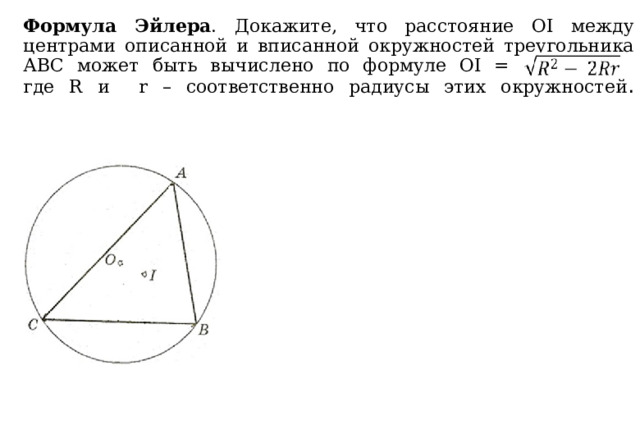
Формула Эйлера . Докажите, что расстояние ОI между центрами описанной и вписанной окружностей треугольника АВС может быть вычислено по формуле OI = , где R и r – соответственно радиусы этих окружностей .

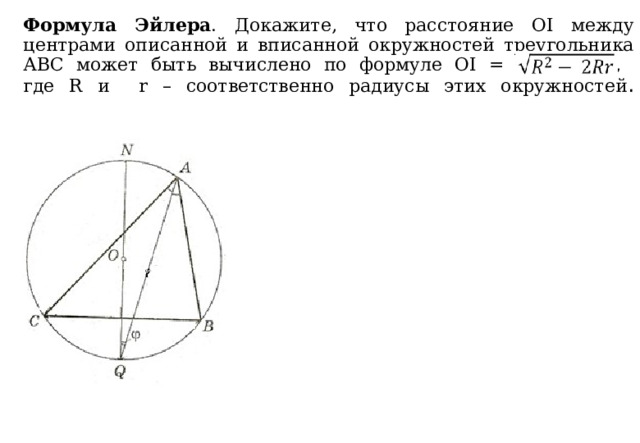
Формула Эйлера . Докажите, что расстояние ОI между центрами описанной и вписанной окружностей треугольника АВС может быть вычислено по формуле OI = , где R и r – соответственно радиусы этих окружностей .

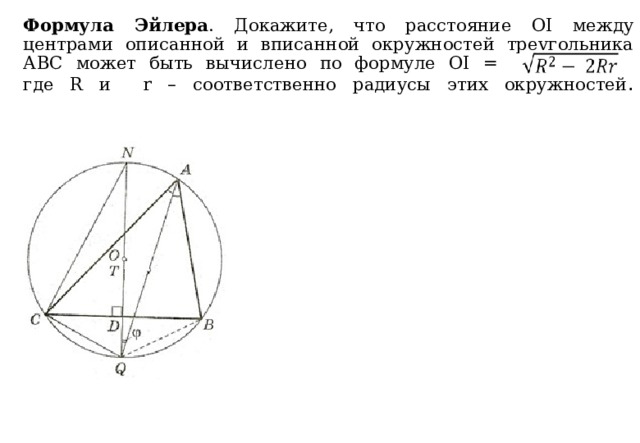
Формула Эйлера . Докажите, что расстояние ОI между центрами описанной и вписанной окружностей треугольника АВС может быть вычислено по формуле OI = , где R и r – соответственно радиусы этих окружностей .

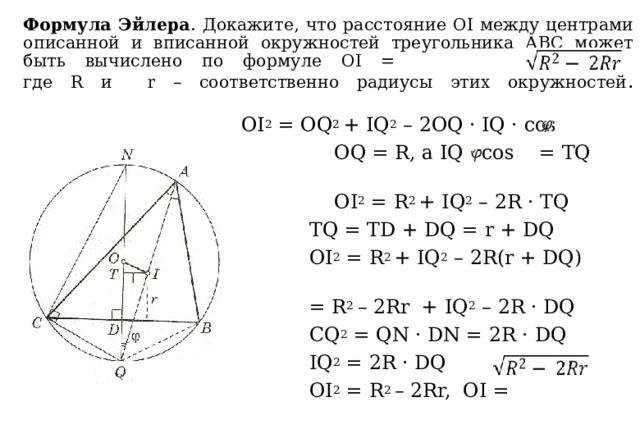
Формула Эйлера . Докажите, что расстояние ОI между центрами описанной и вписанной окружностей треугольника АВС может быть вычислено по формуле OI = , где R и r – соответственно радиусы этих окружностей .

OI 2 = OQ 2 + IQ 2 – 2OQ · IQ · cos

OQ = R, а IQ · cos = TQ

OI 2 = R 2 + IQ 2 – 2R · TQ

TQ = TD + DQ = r + DQ

OI 2 = R 2 + IQ 2 – 2R(r + DQ) =

= R 2 – 2Rr + IQ 2 – 2R · DQ

CQ 2 = QN · DN = 2R · DQ

IQ 2 = 2R · DQ

OI 2 = R 2 – 2Rr, OI =

Задача 1. Доказать для произвольного треугольника АВС справедливость неравенства .

Доказательство.

Задача 2. В треугольнике АВС выполняется соотношение . Доказать, что в таком случае точка О лежит на вписанной в треугольник АВС окружности s.

Доказательство.

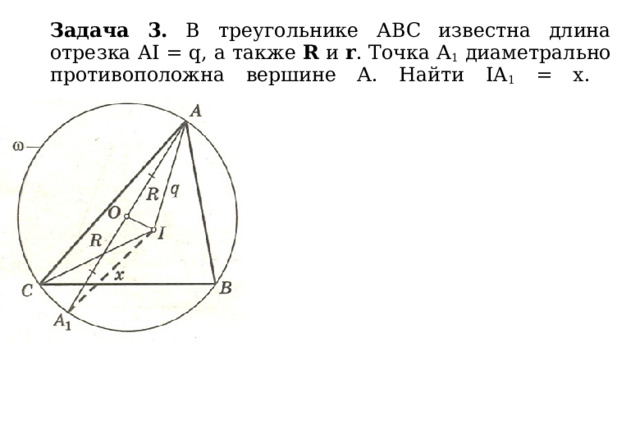
Задача 3. В треугольнике АВС известна длина отрезка AI = q, а также R и r . Точка А 1 диаметрально противоположна вершине А. Найти IA 1 = x.

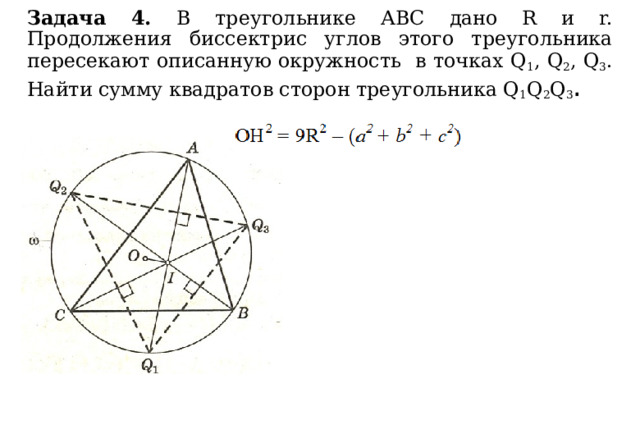
Задача 4. В треугольнике АВС дано R и r. Продолжения биссектрис углов этого треугольника пересекают описанную окружность в точках Q 1 , Q 2 , Q 3 . Найти сумму квадратов сторон треугольника Q 1 Q 2 Q 3 .

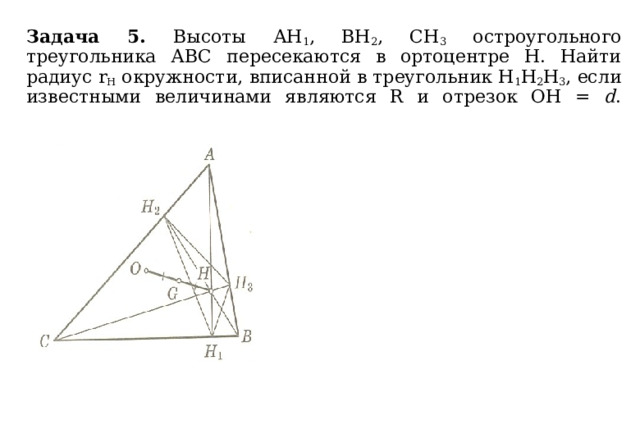
Задача 5. Высоты АН 1 , ВН 2 , СН 3 остроугольного треугольника АВС пересекаются в ортоцентре Н. Найти радиус r H окружности, вписанной в треугольник Н 1 Н 2 Н 3 , если известными величинами являются R и отрезок ОН = d .

Литература

• Заславский А. А. Эйлер и геометрия // Квант, 2007, №3.
• Прасолов В. В. Задачи по планиметрии. Ч.1.// М.: Наука, 1991.
• Шарыгин Г. О некоторых результатах Эйлера в элементарной геометрии // Математика, 2007, №6.

Спасибо за внимание!