Урок на тему: Формула Герона для нахождения площади треугольника
Тип урока: изучение нового.
ЦЕЛЬ: формирование умений учащихся применять формулу Герона к решению задач.
Задачи:
1. Познакомиться с формулой Герона
2. Научиться решать различные задачи (в том числе практико-ориентированные) с её помощью.
Оборудование: проектор, экран, компьютер и доска с мелом.
Ход урока
Учитель: Здравствуйте, ребята!..
Внимание на экран. Давайте вместе с вами определим вид этого треугольника. Какой он?
- прямоугольный
Учитель: А скажите, пожалуйста, как найти его площадь?
- 
Учитель: А что такое a и b?
- это катеты
Учитель: Верно… Смотрите. Они нам известны. Давайте тогда найдем площадь этого треугольника. Чему она равна?
- она равна 20 м2
Учитель: Хорошо. А теперь попробуем найти площадь такого треугольника. Как это можно сделать?
- 
Учитель: Верно. Но как мы найдем, чему равна высота и нужная сторона?
- посчитаем клетки
Учитель: Хорошо. Посчитайте клетки и найдите площадь этого треугольника.
- она равна 12
Учитель: Хорошо. А теперь давайте попробуем найти площадь этого треугольника.
- … высота не дана
Учитель: Верно. В нем нет высоты, нет прямого угла. Возникает вопрос, а можно ли вообще найти площадь такого треугольника. Оказывается можно.
В I веке нашей эры в Греческом городе Александрия жил некий Герон. Философ, математик, инженер. Паровой двигатель, фонтан, автоматы для раздачи, шприц – это лишь немногое, что было сконструировано Героном, а потом спустя почти 2000 лет заново изобретено.
Именно он вывел форму для нахождения любого треугольника по трем сторонам.
Так вот сегодня тема нашего урока: «Формула Герона для нахождения площади треугольника».
Давайте-ка вместе с вами теперь подумаем, а какие цели перед собой мы можем поставить сегодня на уроке? Что мы будем делать? Каких результатов хотим достичь?
{Привести детей к нужной мысли}
Итак. Давайте обобщим всё нами сказанное. Задачи на сегодняшний урок:
1. Познакомиться с формулой Герона
2. Научиться решать различные задачи с её помощью.
Но… Прежде чем знакомиться с формулой Герона, давайте-ка с вами немного поработаем устно. Внимание на экран.
Сейчас перед вами таблица квадратов. Она поможет вам быстро отвечать на мои вопросы. Готовы?..
| а | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| а2 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
Чему равен корень из 2? Округляем ответы до десятых.
- 1,4
Учитель: Чему равен корень из 3?
- 1,7
Учитель: Чему равен корень из 50?
- 7,2
Учитель: Чему равен корень из 63?
- 7,8
Учитель: Хорошо… Усложним задачу. Найдите корень из выражения  ...
...
- 120
Учитель: Я надеюсь, вы же не стали умножать все эти числа… как нашли ответ?..
- отдельно извлекли корень из каждого множителя, а потом умножили.
Учитель: Хорошо… Найдите корень из выражения  … А тут как быть???
… А тут как быть???
- надо 18 и 50 разбить на множители…
{Я пишу на доске!!!! А дети помогают.  }
}
Учитель: Отлично. Ну что ж. Я думаю, вы вполне готовы познакомиться с формулой знаменитого Герона. Открываем свои тетради. Записываем сегодняшнее число, классная работа, а ниже то, что вы сейчас видите на экране (с рисунком).
…
Что ж… С формулой мы познакомились. Давайте попробуем порешать задачи. Сейчас вы будете работать в группах.
{раздаю задания и одновременно их поясняю}
Перед вами три треугольника. Надо найти их площади. В ответ 1-я группа должна записать самую большую из полученных площадей, 2-я группа – самую маленькую из полученных площадей, а 3-я группа – вам надо будет записать в ответ ту площадь, которая является второй по величине. Задание понятно? Приступаем.
…
{Выслушать полученные ответы: группа называет полупериметр и площадь.}
Учитель: А теперь внимание на экран…

Перед вами уже построенный дом. Хозяин дома хочет заменить на нем всю основную черепицу.
Я каждой группе сейчас раздам условия, которые нам известны… {раздаю}
Скажите, пожалуйста, из каких фигур состоит наша крыша…
- из треугольников
Учитель: Из трех различных треугольников, которые можно взять попарно! {показать на слайде}
А еще на одной из сторон крыши есть окно. Это тоже надо учитывать.
Итак… Что в первую очередь мы должны с вами найти?
- площадь всей крыши
Учитель: Как это можно сделать?
- надо найти площадь каждого треугольника, сложить их. Полученную сумму умножить на два. А потом найти и вычесть площадь окна.
Учитель: Хорошо. Дальше? Смотрите на условие. Нам еще дали параметры одной черепицы. Зачем нам это?
- мы найдем и ее площадь.
Учитель: Хорошо. У нас будет общая площадь покрытия крыши и площадь одной черепицы. Как найти, сколько этих самых черепиц нам надо закупить?
- Разделим площадь крыши на площадь черепицы.
Учитель: Отлично. Делаем. Но, чтобы работа шла быстрее разделим обязанности. 1-я группа, вы ищите площадь первого треугольника, 2-я группа – вы площадь второго треугольника, а 3-я группа – вам достался третий треугольник.
Учтите, что сейчас вы можете столкнуться с тем, что число не будет полностью извлекаться из-под корня. Для этого вам дана таблица квадратов. Найдите ответ приближенно и округлите до ЦЕЛОГО значения.
…
{1. Дети называют полученные площади.
2. Я записываю их на доске в столбик и прошу одного ученика выйти к доске и найти их сумму. Следущего ученика прошу умножить результат на 2. Следущего – найти площадь окна. Следующего – найти разность полученных площадей.
3. Ответ я записываю на доске повыше (с единицами измерения!!!!!), чтобы стереь с доски лишнюю информацию.
4. Вместе с детьми находим площадь черепицы (с единицами измерения).}
Учитель: Итак… Вроде как всё найдено. Осталось поделить… Но… Можно уже найти, сколько черепиц нам надо или что-то мешает????
- у них разные единицы измерения!
Верно! Давайте-ка для начала переведем квадратные метры в квадратные сантиметры. Как это сделать?..
- если в 1 м = 100 см, то в 1 м2 = 10 000 см2.
{дописываю нолики и делю числа НА КАЛЬКУЛЯТОРЕ. Если ответ, получился не целым, то спрашиваю у детей, как я должна взять ответ: с избытком или недостатком… Ответ записываем на доску}
Учитель: Доп. задание 1: А теперь давайте усложним задачу. Предположим, что хозяин дома приехал на склад, а черепица продается не поштучно, а в упаковке по 100 штук. Сколько упаковок он должен взять?..
А если нам будет известно, что цена одной упаковки 200 руб, сможем ли мы найти стоимость всей нашей покупки?.. Найдите…
…
Отлично. Молодцы! Я думаю, что мы сегодня вполне помогли хозяину перекрыть свою крышу.
Доп. задание 2: А теперь давайте-ка вместе попробуем решить следующую задачу.

Ваши идеи и предложения. С чего начать?..
{Привести детей к мысли:
1. Найти площадь треугольника по формуле Герона.
2. Используя формулу  , найти указанную высоту}
, найти указанную высоту}
Решение: р = 8, S = 12, тогда АН = 4,8.
Ну что ж, ребята… давайте попробуем подвести итог нашего урока.
Смогли ли мы достигнуть поставленных на сегодня задач?..
Тогда у меня остался к вам последний вопрос: нужно ли изучать формулу Герона? Может ли она нам пригодиться в жизни?..
…
На этом у меня всё. Спасибо за внимание.
Приложение 1
| а | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| а2 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 |



Приложение 2
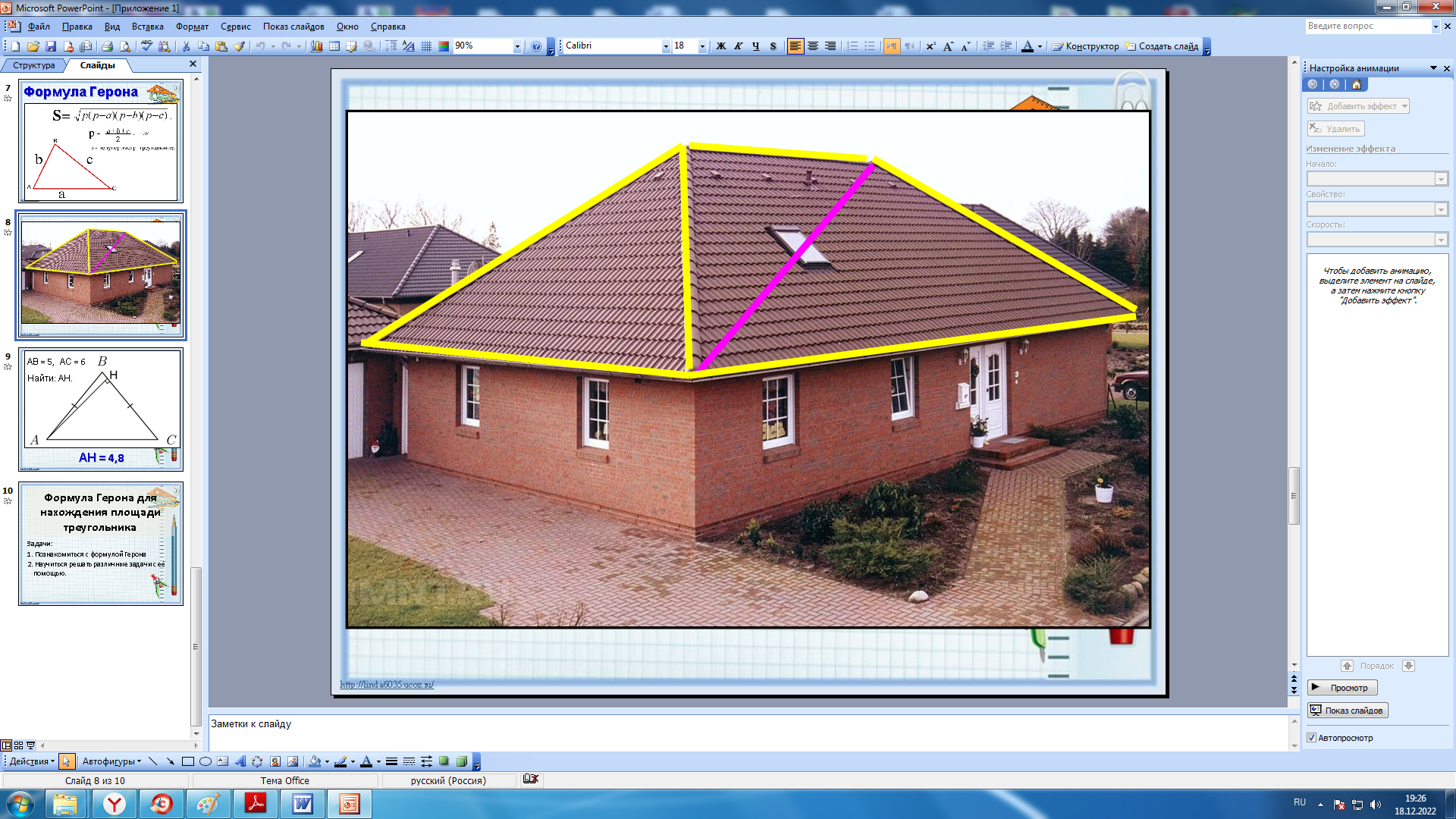

Перед вами уже построенный дом. Хозяин дома хочет заменить на нем всю основную черепицу. Используя следующую информацию, выполните задание: Подсчитайте, сколько черепицы необходимо закупить, чтобы хватило перекрыть всю крышу?
Измерения крыши:


| Измерения окна |
|
| 
|
|
| Измерения черепицы |
|

|
9




























