Формулы для радиусов вписанных и описанных окружностей правильных многоугольников.

Тема урока

Формулы для радиусов

вписанных и описанных окружностей правильных многоугольников.

Выполнил: учитель математики Аюбов Р.К.

Актуализация опорных знаний

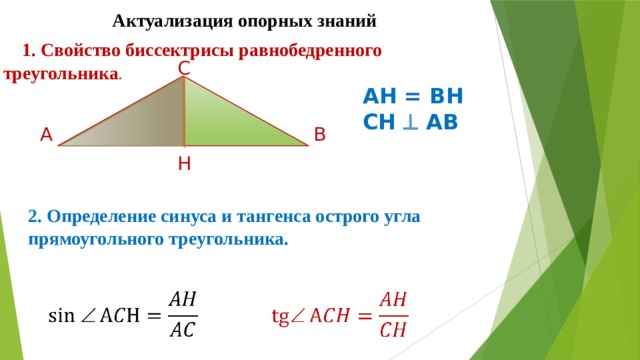
1. Свойство биссектрисы равнобедренного треугольника .

C

AH = BH

CH  AB

A

B

H

2. Определение синуса и тангенса острого угла прямоугольного треугольника.

Цели: ввести формулы, связывающие радиусы R описанной и r вписанной окружностей для правильного многоугольника со стороной а и числом сторон п ; формировать умение применять полученные знания при решении задач; повышение уровня мотивации учащихся к изучению геометрии.

R

r

Высшее проявление духа – это разум.

Высшее проявление разума – это геометрия.

Клетка геометрии – треугольник.

Он так же неисчерпаем, как и вселенная.

Окружность – душа геометрии.

Познайте окружность, и вы не только познаете

Душу геометрии, но и возвысите свою душу.

И.Ф. Шарыгин.

Задачи

1. Найдите угол правильного пятиугольника, шестиугольника, восьмиугольника.

2. Найдите количество сторон правильного многоугольника, если его внутренний угол равен 108 градусам.

1. Найдите угол правильного восьмиугольника.

 =(180  *(п-2))/п

Решение:

 =(180  *(8-2))/8=135 

Ответ: 135  .

2. Найдите количество сторон правильного многоугольника, если его внутренний угол равен 108 градусам.

 =(180  *(п-2))/п

Решение: 108  =(180  *(п-2))/п

180п – 360 = 108п

72п = 360

п = 360 / 72 = 5

Ответ: 5.

Вокруг всякого правильного n-угольника можно описать окружность. Центр окружности – точка пересечения серединных перпендикуляров сторон многоугольника.

В каждый правильный многоугольник можно описать окружность. Центр окружности – точка пересечения биссектрис углов.

Вписанная и описанная окружности правильного многоугольника имеют общий центр. Он называется центром данного правильного многоугольника.

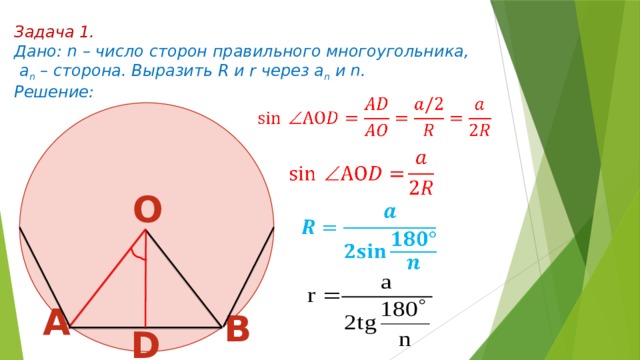
З адача 1.

Дано: n – число сторон правильного многоугольника,

a n – сторона. Выразить R и r через а n и n.

Решение:

О

А

B

D

Задача 2.

Выразить сторону правильного шестиугольника через R и r.

= R,

т.е.

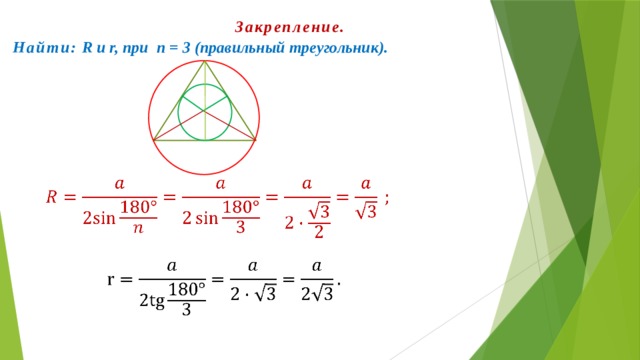
Закрепление.

Найти: R и r, при n = 3 (правильный треугольник).

Задача 17.(В-18)

Найдите площадь квадрата, описанного около окружности радиуса 16.

R

S = 32  32 = = 1024

Ответ: 1024.

Задача 17.(В-6)

Площадь круга 69. Найдите площадь сектора этого

круга, центральный угол которого равен 120  .

Ответ: 23.

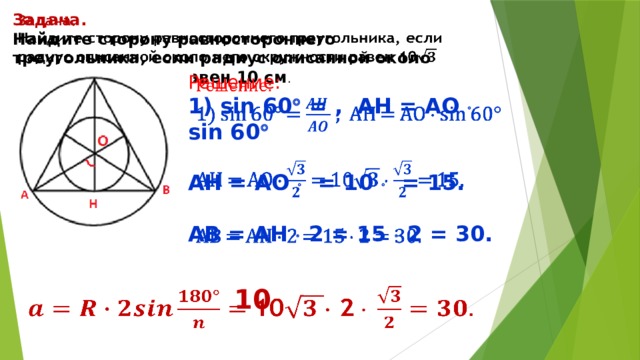
Задача.

Найдите сторону равностороннего треугольника, если радиус описанной около него окружности равен 10 см .

Решение:

1) sin 60  = , AH = AO  sin 60 

AH = AO  = 10  = 15.

AB = AH  2 = 15  2 = 30.

10

Задача.

Найдите площадь квадрата, описанного около круга площадью 25  .

25  =  

r = 5;

1) S =  

2) a = 2  r = 2  5 = 10;

S =

Ответ: 100.

Итог урока.

– У какого выпуклого многоугольника все внешние углы прямые?

– Приведите пример такого выпуклого многоугольника, у которых все стороны равны, но он не является правильным.

Домашнее задание: подготовить тематическую таблицу «Правильный многоугольник»; № 22; № 17 (В7).

ramazan-ark@yandex.ru