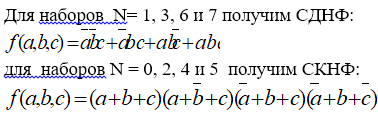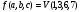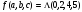Логические функции, СДНФ СКНФ
1.4 Формы представления функций алгебры логики
Функции алгебры логики могут быть заданы различными способами:
- таблицей истинности - в аналитической форме- в числовой форме..
Если функция имеет значения на всех наборах, то она называется полностью определенной.
элементарная дизъюнкция - дизъюнктивный терм или макстерм - это дизъюнктивный терм или макстерм - это дизъюнкция произв числа попарно независимых перем Например, 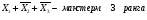
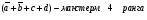
элементарная конъюнкция - конъюнктивный терм или минтерм - конъюнкция произв числа попарно независимых перем. Напр, Х 1Х 2 Х3 - минтерм 3-его ранг
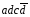 – это не минтерм, так как перем
– это не минтерм, так как перем 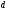 и
и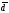 зависимы.
зависимы.
Для аналитической записи функций используют две формы:
1) Дизъюнктивную Нормальную Форму - ДНФ
2) Конъюнктивную Нормальную Форму – КНФ
ДНФ это дизъюнкция минтермов разл ранга 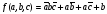
КНФ это конъюнкция макстермов различного ранга
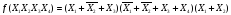
Если все термы, входяшие в нормальную форму имеют одинаковый и максимальный ранг,= числу переменных функции - n, то такая форма называется совершенной. При этом, минтерм называют констинтуентой (составля) 1 (КЕ), а макстерм - конституентой 0 (КН).
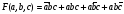 - это СДНФ
- это СДНФ
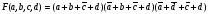 - это СКНФ
- это СКНФ
Т е СДНФ есть дизъюнкция конституент 1, а СКНФ - есть конъюнкция конституент 0
Составление совершенных форм по табл истинности
Совершенные формы составляют по табл истинности функции. СДНФ : для каждого набора переменных на которых функция=1, записывают минтерм ранга n , в которых с отрицанием берутся переменные = 0 на данном наборе. Все минтермы объединены дизъюнктивно.
СКНФ =для каждого набора переменных, на которых функция=0, записывают макстерм ранга n, в кот с отрицанием берутся переменные, имеющие значение=1 на данном наборе. Все макстермы объединены конъюнктивно
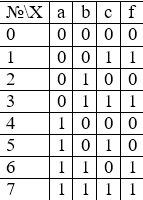
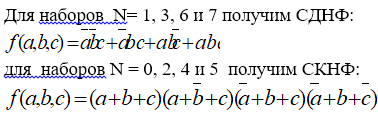
Для компактной записи функций исп числовую форму, в которой заданы только номера наборов. Числовая форма для СДНФ: 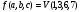
Числовая форма для СКНФ: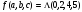
Алгоритм преобразованияя в ДНФ
1) Сначала избавляемся от операций импликации, эквивалентности и неравнозначности, выразив их через логические связки ¬, & и ∨ по законам:
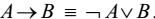
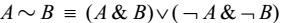
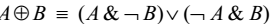
2) Доводят знаки отрицания до независимых переменных, используя законы де Моргана:
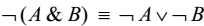
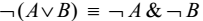
3) Применяя з-н дистрибутивности 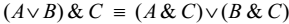
преобразуют формулу к дизъюнкции элементарных конъюнкций
4) 4) Постоянно избавляются от двойных отрицаний: 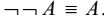
ДНФ A наз совершенной и обозн СДНФ, если каждая переменная формулы A входит с отрицанием или без отрицания в каждый конъюнкт точно 1 раз.
Алгебраическая форма представления булевых функций используется для минимизации (упрощения формулл) и для построения логических схем. Существукт 2 формы алгебраических функций – дизъюнктивная и конъюнктивн. Дизъюнктивная нормальная форма представляет сумму элементарных произведения аргументов, например
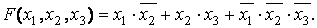
Если кажд слаг содер все арг или их отриц, то получ соверш дизъюнкт норм форму (СДФН), напр
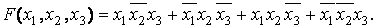
Для перехода от табл истинн к СДНФ учит только те сост, для кот функц= 1. Для каждого такого сост запис элем произв всех ар. Если арг имеет зн "0", то запис его отриц. Для привед примера СДНФ имеет вид 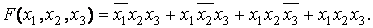 (17.4)
(17.4)
Совершенная конъюнктивная нормальная форма (СКНФ) представляет логическое произведение элементарных логических сумм, причем каждая сумма содержит все аргументы или их отрицания, например
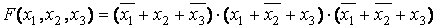
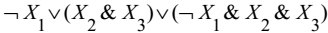 ДНФ, но не СДНФ от 3 перем
ДНФ, но не СДНФ от 3 перем
-ДНФ от 2 перем
-представл импликации в виде ДНФ.
-СДНФ для импликации
-СДНФ для оп эквивалентности
-СДНФ для оп неравнозначности
Прим.1 Привести к ДНФ формулу
Реш.
2. Привести ту же формулу к СДНФ. Начав преобразования с ДНФ
| Нахождение СДНФ по табл истинности функции | Нахождение СКНФ по табл истинности функции |
| 1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 1. 2)Выписать для каждой отмеченной строки конъюнкцию всех переменных так: если значение некоторой переменной в данной строке - 1, то в конъюнкцию включать саму эту переменную, если равно 1, то ее отрицание. 3)Все полученные конъюнкции связать в дизъюнкцию. | 1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 0. 2)Выписать для каждой отмеченной строки дизъюнкцию всех переменных так: если значение некоторой переменной в данной строке= 1, то в дизъюнкцию включать саму эту переменную, если равно 0, то ее отрицание. 3)Все полученные дизъюнкции связать в конъюнкцию. |
Прим1
Прим 2
| построение СДНФ: | построение СКНФ: |
| | |
Для перехода от таблицы истинности к СКНФ учитывают только те состояния, для которых функция= "0". Для каждого такого состояния записывается элементарная сумма аргументов. Если аргуент имеет значение "1", то пишут его отрицание. Для примера СКНФ имеет вид
Примеры
1)Привести к КНФ и СКНФ.
Реш. упростим выражение, используя законы де Моргана и правило x y x y → = ∨
Теперь приводим к КНФ
Приведем к СКНФ:
2) С помощью эквивалентных преобразований построить д.н.ф. функции f (x):
Решение. Преобразуем функцию:

3) Используя СКНФ, найти наиболее простую формулу алгебры высказываний от 4 переменных, принимающую значение 0 на следующих наборах значений переменных, и только на них:
Решение. Запишем СКНФ функции по данным задачи

Получили
ЛИТЕРАТУРА и ССЫЛКИ
1)Курилова М.Н. Информатика-логика, СПБ Лес-техн ун-т им.Кирова
https://studfiles.net/preview/2069515/page:5/
2) http://ptca.narod.ru/lec/lec4_3.html
3) https://www.matburo.ru/ex_dm.php?p1=bfpg







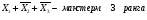
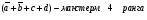
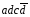 – это не минтерм, так как перем
– это не минтерм, так как перем 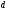 и
и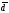 зависимы.
зависимы.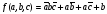
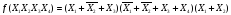
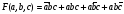 - это СДНФ
- это СДНФ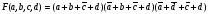 - это СКНФ
- это СКНФ