Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа 17
имени А.А. Герасимова
Исследовательская работа по теме
«Геометрические фракталы»
Выполнила: Головко Дарья, ученица 10 класса.
Научный руководитель:
Качалова Елена Сергеевна.
г. Рыбинск
2022г.
Содержание
Введение……………………………………………………………………………2 стр.
Глава 1. Теоретическая часть.
Понятие фрактала. История возникновения……………………………...4 стр.
Геометрические фракталы…………………………………………………5 стр.
Виды геометрических фракталов………………………………………….6 стр.
Глава 2. Практическая часть.
2.1. Исследование. Применение фракталов в жизни…………………………….8 стр.
2.2. Построение фракталов ………………………………………………………..9стр.
Заключение…………………………………………………………………….......10 стр.
Информационные ресурсы ……………………………………………………….11стр.
Приложение ………………………………………………………………………..12 стр.
Введение.
Математика – древнейшая наука. Большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, многоугольник, сфера и т.д. Как оказалось, многие природные системы настолько сложны, что использование только знакомых объектов обычной геометрии для их моделирования представляется безнадежным. Как, к примеру, построить модель горного хребта или кроны дерева в терминах геометрии? Как описать то многообразие биологических разнообразий, которое мы наблюдаем в мире растений и животных? Как представить всю сложность системы кровообращения, состоящей из множества капилляров и сосудов и доставляющей кровь к каждой клеточке человеческого тела? Представить строение легких и почек, напоминающие по структуре деревья с ветвистой кроной?
Фракталы - подходящие средства для исследования поставленных вопросов. Нередко то, что мы видим в природе, интригует нас бесконечным повторением одного и того же узора, увеличенного или уменьшенного во сколько-то раз. Например, у дерева есть ветви. На этих ветвях есть ветки поменьше и т.д. Теоретически, элемент «разветвление» повторяется бесконечно много раз, становясь все меньше и меньше. То же самое можно заметить, разглядывая фотографию горного рельефа. Попробуйте немного приблизить изображение горной гряды - вы снова увидите горы. Так проявляется характерное для фракталов свойство самоподобия.
Для многих хаологов (ученых изучающих фракталы и хаос) - это не просто новая область познания, которая объединяет математику, теоретическую физику, искусство и компьютерные технологии - это революция. Это открытие нового типа геометрии, той геометрии, которая описывает мир вокруг нас и которую можно увидеть не только в учебниках, но и в природе и везде в безграничной вселенной.
По сути, фракталы открывают нам глаза и позволяют посмотреть на графику, с другой стороны. Казалось бы, производятся обычные расчёты с обычными «сухими» цифрами, но это даёт нам по-своему уникальные результаты, позволяющие почувствовать себя творцом природы. Фракталы дают понять, что это наука о прекрасном.
Своей проектной работой я хотела узнать о довольном новом понятии «фрактал». Что это такое, какие существуют виды, где распространяются. Я очень надеюсь, что фракталы заинтересуют вас. Ведь, как оказалось, фракталы довольно интересны, и они есть почти на каждом шагу.
Актуальность проекта: состоит в том, что открытие теории фракталов – это открытие не просто новой области познания, которая объединяет математику, физику, искусство и компьютерные технологии – это революция. Это открытие нового типа геометрии, той геометрии, которая описывает мир вокруг нас и которую можно увидеть не только в учебниках, но и в природе и везде в бесконечной вселенной.
Цель работы: Изучение геометрических фракталов, их разновидности.
Задачи:
Изучить литературу по данной теме.
Понять, что такое фрактал
Рассмотреть некоторые виды фракталов, найти их в окружающей среде
Понять их значимость в мире
Создать собственные фракталы
Глава 1. Теоретическая часть
1.1.Понятие фрактала. История возникновения.
Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».
Фрактал (лат. fractus — дробленый, сломанный, разбитый) — термин, означающий сложную геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком.
Фракталы — это не линии и не поверхности, а, если можно это себе представить, нечто среднее. С ростом размеров возрастает и объем фрактала, но его размерность (показатель степени) — величина не целая, а дробная, а потому граница фрактальной фигуры не линия: при большом увеличении становится видно, что она размыта и состоит из спиралей и завитков, повторяющих в малом масштабе саму фигуру. Такая геометрическая регулярность называется масштабной инвариантностью или самоподобием. Она-то и определяет дробную размерность фрактальных фигур.
1.2. Геометрические фракталы.
Именно с этого вида фракталов началась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется набор отрезков, на основании которых будет строиться фрактал. Далее к ним применяют набор правил, который преобразует их в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем бесконечное количество преобразований, то получим геометрический фрактал. Геометрические фракталы являются самыми наглядными, так как обладают так называемой жесткой самоподобностью (т.е. объект, в точности или приближённо совпадающий с частью себя самого), не изменяющейся при изменении масштаба. Это значит, что, независимо от того, насколько вы приближаете фрактал, вы видите всё тот же узор.Геометрические фракталы с одной стороны, являются предметом серьезного научного изучения, а с другой — даже человек, далекий от математики, найдет в них что-то для себя. Такое сочетание редко встречается в современной математике, где все объекты задаются с помощью непонятных слов и символов. Многие геометрические фракталы можно нарисовать на листочке бумаги в клетку.
1.3. Виды геометрических фракталов.
На сегодняшний день можно выделить несколько основных геометрических фракталов.
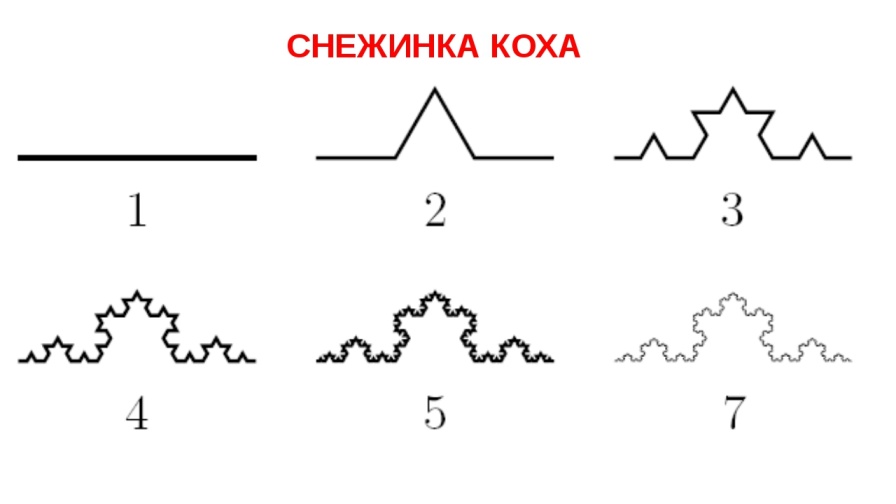
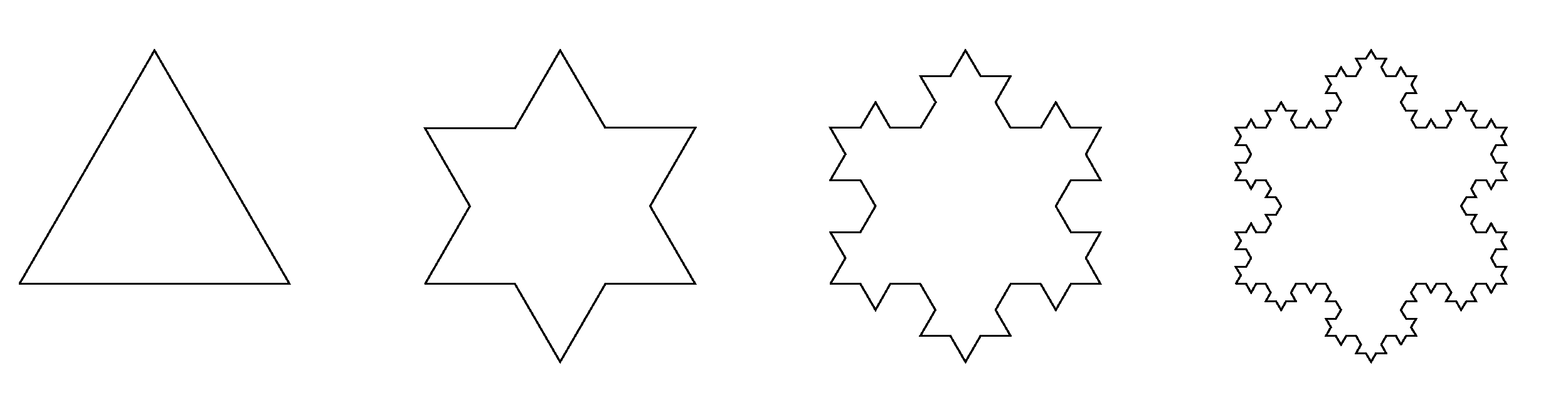
1) Снежинка Коха. Эта фигура — один из первых, исследованных учеными фракталов. Она получается из трех копий кривой Коха, которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Рисунок отлично показывают, как по шагам строится кривая Коха. Первая итерация (т.е. повторение какого-либо действия) — просто начальный отрезок. Потом он делится на три равные части, центральная достраивается до правильного треугольника и затем выкидывается. Получается вторая итерация — ломаная линия, состоящая из четырех отрезков. К каждому из них применяется такая же операция, и получается четвертый шаг построения. Продолжая в том же духе, можно получать всё новые и новые линии (все они будут ломаными). А то, что получится в пределе (это уже будет воображаемый объект), и называется кривой Коха. (приложение 1)
2) Т-квадрат. Этот фрактал получил такое название за сходство с рейсшиной — линейкой с приделанной перпендикулярной планкой в виде буквы Т. Построение начинается с синего единичного квадрата. Первый шаг: закрасить в центре белым цветом квадрат со стороной 1/2. Затем нужно мысленно разделить квадрат на 4 одинаковых квадрата и в центре каждого из них закрасить квадрат со стороной 1/4. Дальше каждый из этих 4 квадратов снова делится на 4 части, всего получится 16 квадратиков, и с каждым из них нужно проделать то же самое. И так далее. (приложение 2)
3) H-фрактал. Всё начинается с фигуры в виде буквы Н, у которой вертикальные и горизонтальные отрезки равны. Затем к каждому из 4 концов фигуры пририсовывается ее копия, уменьшенная в два раза. К каждому концу (их уже 16) пририсовывается копия буквы Н, уменьшенная уже в 4 раза. И так далее. В пределе получится фрактал, который визуально почти заполняет некоторый квадрат. Н-фрактал всюду плотен в нём. То есть в любой окрестности любой точки квадрата найдутся точки фрактала. Очень похоже на то, что происходит с Т-квадратом. Это не случайно, ведь, если присмотреться, видно, что каждая буква Н содержится в своем маленьком квадратике, который был дорисован на таком же шаге. (приложение 3)
4) Треугольник Серпинского. Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться «в обратном направлении»: взять изначально «пустой» треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т. д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут. (приложение 4)
5) Дерево Пифагора. Оно называется так потому, что каждая тройка попарно соприкасающихся квадратов ограничивает прямоугольный треугольник и получается картинка, которой часто иллюстрируют теорему Пифагора.Хорошо видно, что всё дерево ограничено. Если самый большой квадрат единичный, то дерево поместится в прямоугольник 6 × 4. Значит, его площадь не превосходит 24. Но с другой стороны, каждый раз добавляется в два раза больше троек квадратиков, чем в предыдущий, а их линейные размеры в √2 раз меньше. Поэтому на каждом шаге добавляется одна и та же площадь, которая равна площади начальной конфигурации (взаимное расположение предметов; соотношение составных частей сложных предметов.), то есть 2. Казалось бы, тогда площадь дерева должна быть бесконечна! Но на самом деле противоречия здесь нет, потому что довольно быстро квадратики начинают перекрываться, и площадь прирастает не так быстро. Она всё-таки конечна, но, по всей видимости, до сих пор точное значение неизвестно, и это открытая проблема. (приложение 5)
6) Кривая Леви. За сходство с буквой «С», написанной витиеватым шрифтом, ее еще называют С-кривой Леви. Если приглядеться, то можно заметить, что кривая Леви похожа на форму кроны дерева Пифагора. (приложение 6)
7) Кривая дракона. Считается, что такое название фрактал получил за сходство с традиционными китайскими драконами. По крайней мере, так показалось ученым, которые впервые его исследовали. Каждая ломаная-дракон является лишь приближением к дракону-фракталу и состоит из отрезков.На каждом шаге нужно заменить каждый из отрезков, составляющих данную ломаную, на уголки — стороны равнобедренного прямоугольного треугольника, у которого этот отрезок является основанием. При этом нужно поочередно откладывать эти треугольники то влево, то вправо по ходу движения от одного конца ломаной к другому. (приложение 7)
Глава 2. Практическая часть.
2.1. Исследование. Применение фракталов в жизни.
Фракталы в нашей жизни на данный момент имеют колоссальное значение. Рассмотрим некоторые области применения фракталов и фрактальной геометрии:
Телекоммуникации. Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес и увеличивает качество принимаемого сигнала. (приложение 8)
Биология и медицина. Сам по себе человеческий организм состоит из множества фракталоподобных структур: Кровеносная, дыхательная, нервная система, сетчатка глаза - вот только самый беглый список биологических фракталов, которые присутствуют в каждом человеке. (приложение 9)
Природа. Природа создаёт удивительные и прекрасные фракталы, с безупречной геометрией и идеальной гармонией. Природа сама создана из самоподобных фигур, просто мы этого не замечаем. (приложение 10)
Архитектура. В архитектуре применяются геометрические фракталы.Все они получены путем повторений определенной последовательности геометрических построений с использованием точек и линий. (приложение 11)
Компьютерная графика. Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и т. д. С помощью этого метода создаются реалистичные изображения природных объектов, таких, например, как листья папоротника, деревья при этом неоднократно применяются преобразования, которые двигают, изменяют в размере и вращают части изображения. (приложение 12)
2.2. Построение фракталов.
Выше мы дали определение фракталов, узнали историю возникновения, рассмотрели различные их виды. Меня заинтересовало: как можно самой построить такие фракталы?
Чтобы нарисовать фрактал, воспользуемся треугольником Серпинского (один из видов фракталов, который я нарисовала). В качестве основной фигуры здесь используется равносторонний треугольник. Отмечаем середину на каждой из его сторон. Затем соединяем линиями эти три точки. В результате, внутри нашего треугольника образуются ещё три треугольника, но уже меньшего размера. Далее повторяем дробление каждого из этих трёх треугольников. Получаем уже девять новых фигур. И так до бесконечности. И всё это множество находится внутри первоначального треугольника. Поэтому при приближении картинки в электронном виде возникает ощущение бесконечности.
В ходе работы над фракталами я поняла, что необходимо соблюдать алгоритм в основу которого берётся отрезок или геометрическая фигура.В дальнейшем пройдя через множествоитераций (т.е. повторение какого-либо действия), фигура будет становиться всё сложнее и сложнее.
Считаю, что практическая значимость данной работы заключается в следующем:
Изучив литературу по данному вопросу, я получила дополнительные знания в области математики, укрепив свой интерес к этой науке;
При изучении данной темы приобретенные знания и навыки исследовательской работы я хочу продолжить развивать в будущем
Мое исследование может быть полезно, как другим учащимся, так педагогам
Заключение.
Данная тема показалась мне уникальной и занимательной. Раньше я не имела представления о фракталах и не знала, что это такое, но, познакомившись с ними, поняла, что фрактал - нередкое явление в нашей жизни. Мы буквально окружены ими. Фракталы встречаются везде, и без их существования мир оказался бы скучным и простым. Они украшают нашу жизнь, задают форму предметам, заставляют остановиться и присмотреться к тому что нас окружает. Даже человек далекий от математики с лёгкостью может заметить фрактал и поймет его красоту.
Анализируя выполнение поставленных задач, можно сказать следующее: в моей исследовательской работе я познакомилась с историей возникновения и развития фрактальной геометрии; изучила виды фракталов, их применение в современном мире; создала собственные фракталы, что явилось продуктом данной работы. Данная работа является введением в мир фракталов. Я рассмотрела только самую малую часть того, какие бывают фракталы, на основе каких принципов они строятся. В моей работе приведены далеко не все области человеческих знаний, где нашла свое применение теория фракталов. Хочу только сказать, что со времени возникновения теории прошло не более трети века. Открытие фракталов произвело революцию не только в геометрии, но и в физике, химии, биологии. Фрактальные алгоритмы нашли применение и в информационных технологиях.
Фрактальная наука еще очень молода, и ей предстоит большое будущее.
Информационные ресурсы.
1.https://elementy.ru
2.https://school-science.ru
3.https://dic.academic.ru
4.https://www.techinsider.ru
Приложение 1.
Приложение 2.

Приложение 3.

Приложение 4.
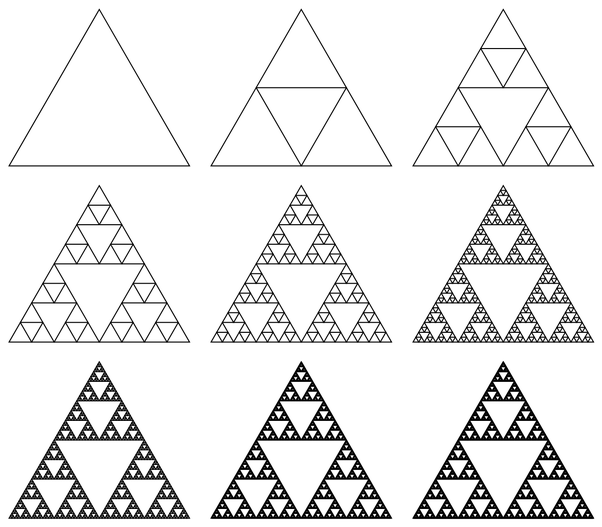
Приложение 5.
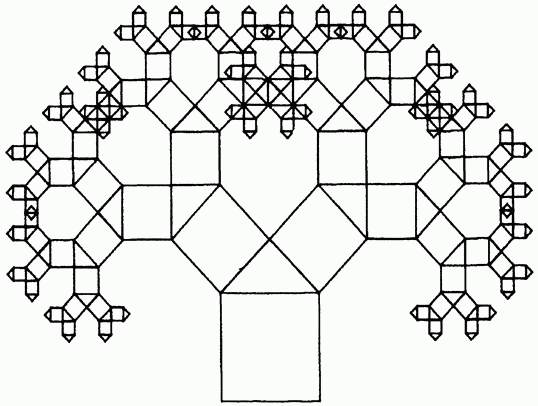
Приложение 6.
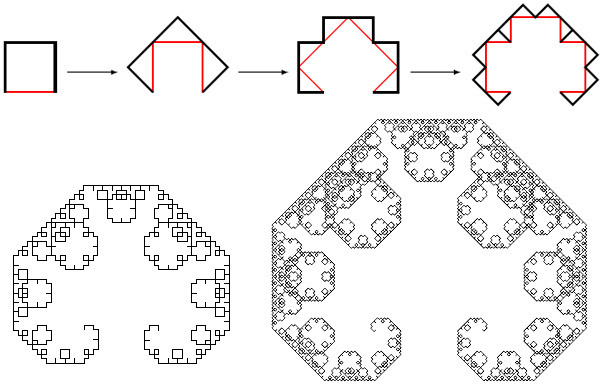
Приложение 7.

Приложение 8.


Приложение 9.
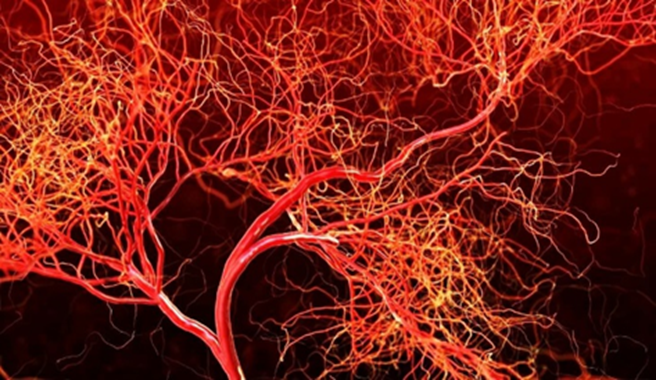
 Приложение 10.
Приложение 10.
Приложение 11.

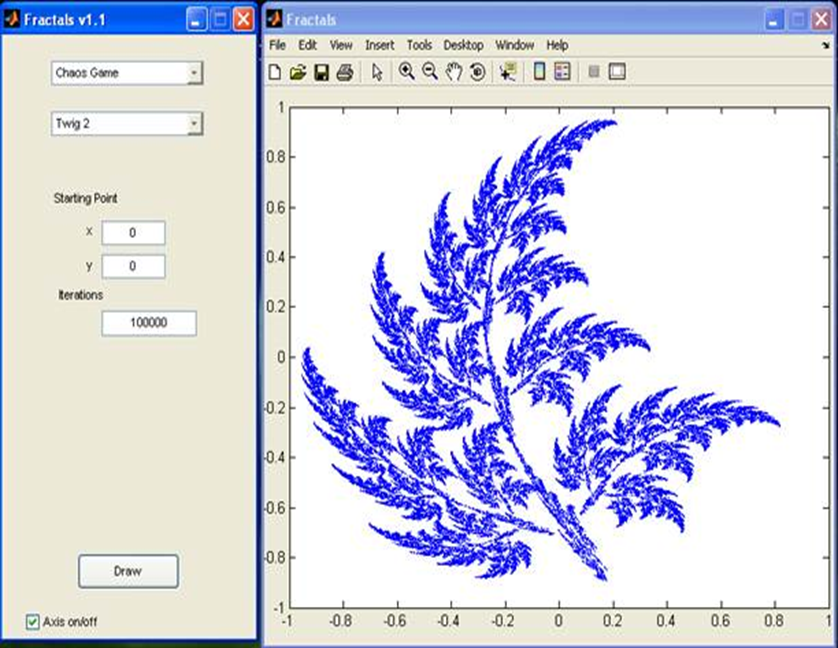 Приложение 12.
Приложение 12.

















 Приложение 10.
Приложение 10.
 Приложение 12.
Приложение 12.









