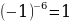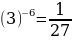Технологическая карта урока
Предмет: Алгебра
Класс: 9 класс
Учебник: Мордкович. 9 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. – 12-е изд., стер. – М. : Мнемозина, 2010 – 224 с. Глава 3. §13.
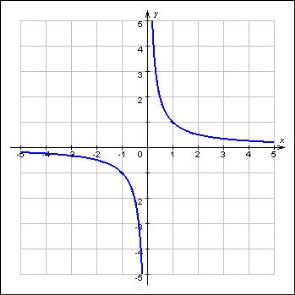
Тема урока: Функции 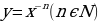 , их свойства и графики.
, их свойства и графики.
Тип урока: урок - семинар
Учебная задача урока: в ходе групповой работы изучить свойства и график степенной функции с отрицательным целым показателем.
Диагностируемые цели урока: в результате урока ученик
Знает:
определение степенной функции с целым отрицательным показателем;
вид графика и свойства функций у = х–2n, где n – натуральное число
вид графика и свойства функций у = х–(2n-1) , где n – натуральное число
Умеет:
строить графики степенной функции с целым отрицательным показателем;
перечислять свойства функций вида у = х–2n, где n – натуральное число
перечислять свойства функций вида у = х–(2n-1) , где n – натуральное число
доказывать четность/нечетность функций вида у = х–2n, где n – натуральное число
доказывать возрастание/убывание функций вида у = х–(2n-1) , где n – натуральное число
Понимает:
как построить график функции вида у = х–(2n-1) , где n – натуральное число
как построить график функции вида у = х–2n, где n – натуральное число
как получены свойства функции вида у = х–(2n-1) , где n – натуральное число
как получены свойства функции вида у = х–2n, где n – натуральное число
Планируемые результаты (УУД):
Личностные: умение учащегося устанавливать связи между целью учебной деятельности и ее мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом должна осуществляться осмысленная организация собственной деятельности ученика.
Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно, планирование – определение последовательности промежуточных целей с учетом конечного результата, оценка – выделение и осознание учащимся того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т.е. определение цели сотрудничества, функций учеников, способов взаимодействия, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.
Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных); выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей.
Подготовка к семинару:
За 2 недели до урока учитель объявляет тему семинара, разбивает учащихся на группы, раздает темы выступлений и список литературы для каждой из групп.
1 группа. «Функции у=x- 1 и у=x- 3, их свойства и графики»
Литература:
Алгебра. 9 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, П.В. Семенов. – 12-е изд., стер. - М.: Мнемозина, 2010. – 224 с. : ил.
Алгебра. Mathway. https://www.mathway.com/ru/Algebra Дата обращения: 14.04.2021.
Интернет урок. https://interneturok.ru/lesson/algebra/9-klass/chislovye-funktsii/stepennaya-funktsiya-y-x-sup-2n-sup-ee-svoystva-i-grafik Дата обращения: 13.04.2021.
2 группа. «Функция вида y=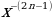 , где n-натуральное число, ее свойства и график»
, где n-натуральное число, ее свойства и график»
Литература:
Алгебра. 9 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, П.В. Семенов. – 12-е изд., стер. - М.: Мнемозина, 2010. – 224 с. : ил.
ЯКласс. https://www.yaklass.ru/p/algebra/9-klass/chislovye-funktcii-svoistva-chislovykh-funktcii-9132/stepennaia-funktciia-s-otritcatelnym-tcelym-pokazatelem-12093/re-7b2783fd-7e69-44f9-b775-cbdf5040d312 Дата обращения: 13.04.2021.
Алгебра. Степенные функции. https://www.mathway.com/ru/Algebra Дата обращения: 14.04.2021.
Интернет урок. https://interneturok.ru/lesson/algebra/9-klass/chislovye-funktsii/stepennaya-funktsiya-y-x-sup-2n-sup-ee-svoystva-i-grafik Дата обращения: 114.04.2021.
3 группа. «Функции 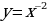 ,
, 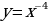 , их свойства и график»
, их свойства и график»
Литература:
Алгебра. 9 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, П.В. Семенов. – 12-е изд., стер. - М.: Мнемозина, 2010. – 224 с. : ил.
Интернет урок. https://interneturok.ru/lesson/algebra/9-klass/chislovye-funktsii/stepennaya-funktsiya-y-x-sup-2n-1-sup-ee-svoystva-i-grafik Дата обращения: 14.04.2021.
Экзамен в школе. Степенная функция. https://dp-adilet.kz/stepennaya-funkciya-y-x-2n-1-ee-svojstva-i-grafik/ Дата обращения: 14.04.2021.
Основные элементарные функции их свойства и графики. https://www.bestreferat.ru/referat-263967.html Дата обращения: 14.04.2021.
Курсотека. 9 класс. Алгебра. https://www.kursoteka.ru/course/3752/lesson/12646/unit/31009 Дата обращения: 14.04.2021.
4 группа. «Функция вида y=x-2n, где n-натуральное число, её свойства и график»
Литература:
1. Алгебра. 9 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович, П.В. Семенов. – 12-е изд., стер. - М.: Мнемозина, 2010. – 224 с. : ил.
2. Алгебракласс. Степенная функция. http://www.algebraclass.ru/kubicheskaya-funkciya/ дата обращения 13.04.2021.
3. Кудрявцев. Функции. http://fizmat.by/math/function/quadratic_function/ дата обращения 13.04.2021.
4. Якласс. Алгебра. 9 класс. Числовые функции. http://www.yaklass.ru/p/algebra/9-klass/chislovye-funktcii-9132/stepennaia-funktciia-s-naturalnym-pokazatelem-12044/re-c7626d3e-e29a-41e9-970f-1a5540f90427/ дата обращения 13.04.2021.
5. Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с.
За неделю до выступлений учитель проверяет все доклады групп и вывешивает план семинара.
План семинара:
Выступление 1 группы: Функции у=x- 1 и у=x- 3, их свойства и графики;
Выступление 2 группы: Функция вида y=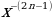 , где n-натуральное число, ее свойства и график;
, где n-натуральное число, ее свойства и график;
Выступление 3 группы: Функции 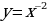 ,
, 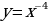 , их свойства и график;
, их свойства и график;
Выступление 4 группы: Функция вида y=x-2n, где n-натуральное число, её свойства и график.
Организационная структура урока
| Этап урока | Деятельность учителя | Деятельность учащихся |
|
|
| Познавательная | Коммуникативная | Регулятивная |
|
| Осуществляемые действия | Осуществляемые действия | Формируемые способы деятельности | Осуществляемые действия | Формируемые способы деятельности | Осуществляемые действия | Формируемые способы деятельности |
| Организационный момент. | Приветствует учащихся. Отмечает отсутствующих. Проверяет готовность учащихся к уроку. Сообщает тему и структуру урока | Отвечают на вопросы учителя по поводу отсутствия учащихся. Настраиваются на работу. | Постановка цель деятельности как ответ на вопрос: «Что я хочу узнать сегодня на уроке?». | Взаимодействуют с учителем во фронтальном режиме. Концентрируют внимание.
| Слушать и слышать собеседника. Планирование учебного сотрудничества с учителем и одноклассниками. | Получают позитивный заряд. | Самоопределение и настраивание на урок. |
| Актуализация знаний. Мотивация. Создание проблемной ситуации. Формирование проблемы: тема и цель урока | Вы все готовились к этому уроку, работая по своим темам. | Цель урока - изучить функции y=x-n (n – натуральное число), их свойства и графики. | Составление плана достижения цели и определения средств её достижения. | Взаимодействуют с учителем во фронтальном режиме. Выходят на необходимость изучения функций y=x-n (n – натуральное число), их свойств и графиков. | Слушать и слышать собеседника. Выражение своих мыслей с достаточной полнотой и точностью, использование дополнительных высказываний для обоснования своего суждения. | Участвуют в диалоге и выводят необходимость изучить функции y=x-n (n – натуральное число), их свойства и графики. | При возникновении ситуации затруднения регулировка хода мысли. |
| «Открытие» нового знания | Организует изучение функций y=x-n (n – натуральное число), их свойств и графиков: см. приложение1. | Учатся применять определения области определения, множества значений функции, четности/ нечетности функции, убывания и возрастания функции в процессе «открытия» нового знания | Выделение необходимой информации, планирование своей деятельности, прогнозирование результата | Взаимодействуют с учителем во фронтальном режиме. Отвечают на задаваемые вопросы в процессе обсуждения, сотрудничают в поиске и выборе информации. Учащиеся выступают с докладами по группам. | Слушать и слышать собеседника. Выражение своих мыслей с достаточной полнотой и точностью, использование дополнительных высказываний для обоснования своего суждения. | Участвуют в диалоге. При необходимости исправляют ошибки, добавляют аргументацию.
| Проявление познавательной инициативы. При возникновении ситуации затруднения регулировка хода мысли. |
| Рефлексия | Организует обсуждение как ответы на вопросы: «Какова была цель урока? Достигли мы её? Как мы её достигли?». | Отвечают на вопросы: «Какова была цель урока? Достигли мы её? Как мы её достигли?». | Рефлексия способов и условий своих действий. | Взаимодействуют с учителем во фронтальном режиме.
| Слушать и слышать собеседника. Использование различных критериев для обоснования своих суждений. | Участвуют в диалоге. При необходимости исправляют ошибки, добавляют аргументацию.
| Проведение самооценки. |
| Домашнее задание | Глава 3, §13. №13.7-13.8 (в, г). №1. Найдите наименьшее и наибольшее значения функции y=x-3 а) на отрезке [-3;-1]; б) на луче [2; + ∞) №2. Найдите наименьшее и наибольшее значения функции y=x-6 а) на отрезке [2;3]; б) на луче (-; -1].
Решение: №1. Найдите наименьшее и наибольшее значения функции y=x-3 а) на отрезке [-3;-1] Решение: y=x-3 убывает на промежутке (–∞; 0) yнаим = y(-1)=(-1)-3= -1; yнаиб = y(-3)=(-3)-3= 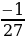 б) на луче [2; + ∞) Решение: y=x-3 убывает на промежутке (0; +∞) yнаим - не существует; yнаиб = y(2)=(2)-3 =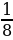 №13.7. Найдите наименьшее и наибольшее значения функции y=x-4 в) на полуинтервале (-3;-1] Решение: y=x-4 возрастает на интервале (-∞;0) yнаим - не существует; yнаиб = y(-1)=(-1)-4= 1 г) на луче [3;+ ∞) Решение: y=x-4 убывает на интервале (0;+∞) yнаим - не существует; yнаиб = y(3)=(3)-4 =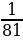 №13.8. Найдите наименьшее и наибольшее значения функции y=x-5 в) на полуинтервале (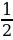 ;4] ;4] Решение: y=x-5 убывает на промежутке (0; +∞) yнаим = y(4)=(4)-5= 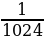 ; yнаиб - не существует ; yнаиб - не существует г) на луче [2;+ ∞) Решение: y=x-5 убывает на промежутке (0; +∞) yнаим - не существует; yнаиб = y(2)=(2)-5 =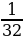 №2. Найдите наименьшее и наибольшее значения функции y=x-6 а) на отрезке [2;3] Решение: y=x-6 убывает на интервале (0;+∞) yнаим = 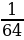 ; yнаиб= ; yнаиб= 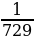 б) на луче (-; -1]. Решение: y=x-6 возрастает на интервале (-∞;0) yнаим - не существует; yнаиб = y(-1)=(-1)-6=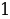 |
Приложение 1.
Выступление 1 группы: «Функции у=x - 1 и у=x - 3, их свойства и графики»
Рассмотрим функцию y=x-1 или 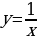 .
.
Свойства:
1.D(f): x 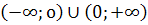 .
.
2. E(x)=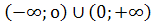 . При x 0 f (x) 0.
. При x 0 f (x) 0.
3. Нечетная.
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 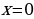 ; это симметричное множество.
; это симметричное множество.
Далее имеем 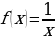 ,
,
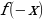 =
=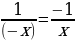 , таким образом,
, таким образом, 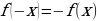 , а значит
, а значит 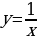 – нечетная функция.
– нечетная функция.
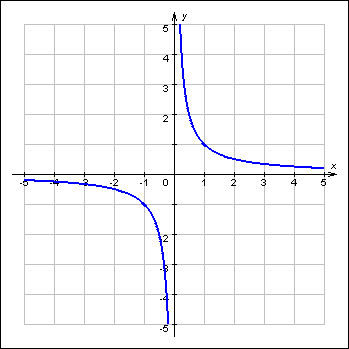
Тогда по свойству нечетной функции, чтобы построить график функции y=x-1, нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от начала координат.
4. Убывает на промежутках (–∞; 0) и (0; +∞).
Докажем это.
1 случай: х0.
Пусть 0x12, значит 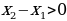 ,
, 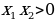 .
. Имеем: у(x1)=
Имеем: у(x1)= 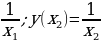 . Рассмотрим
. Рассмотрим 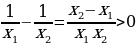 . Значит функция
. Значит функция 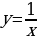 убывает при х0.
убывает при х0.
2 случай: х.
Пусть x1x2 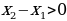 ,
, 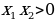 . Имеем: у(x1)=
. Имеем: у(x1)= 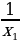 ;
;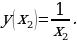 Рассмотрим
Рассмотрим 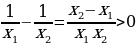 . Значит функция
. Значит функция 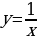 убывает при х
убывает при х
5. Не ограничена ни снизу, ни сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.
7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вниз при 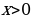 , выпукла вверх при
, выпукла вверх при 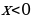 .
.
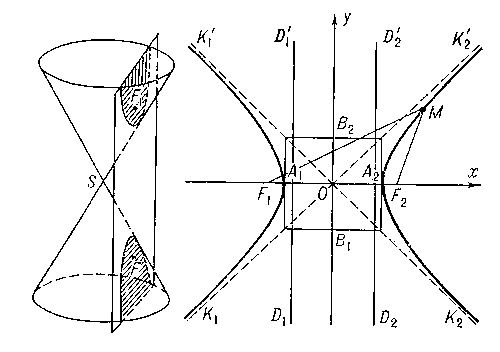
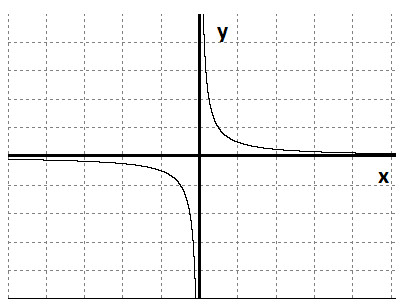
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).
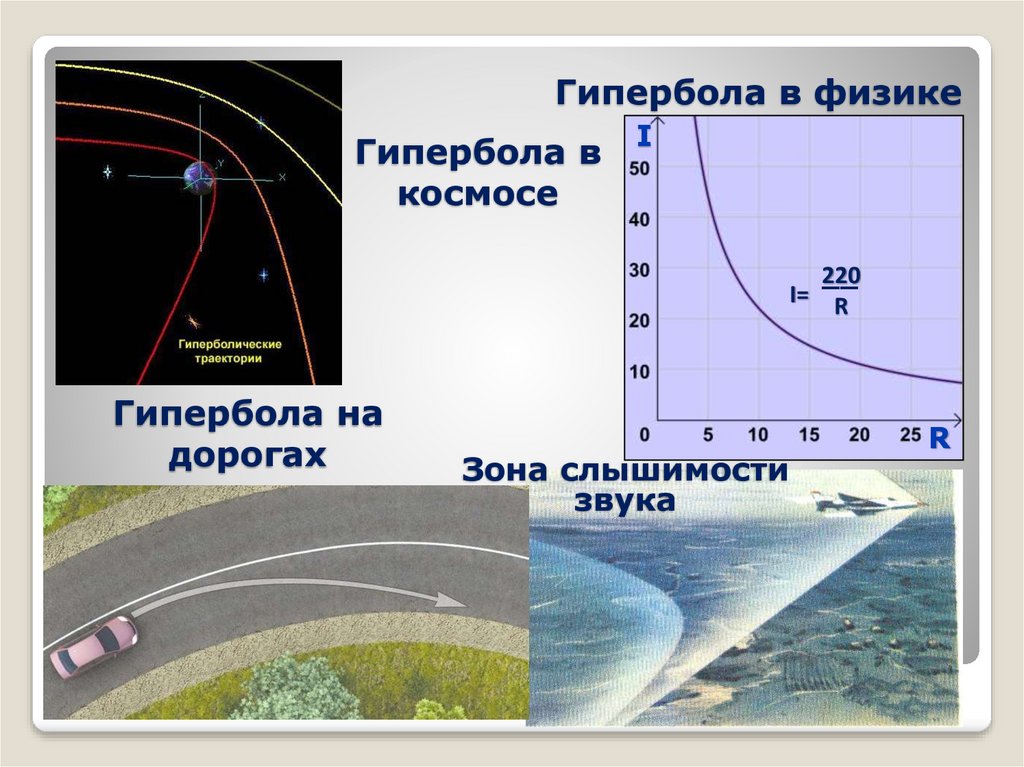
Графики функций вида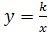 , где k≠0, в частности, график функции
, где k≠0, в частности, график функции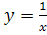 называются гиперболами.
называются гиперболами.
Аналогичные свойства имеет функция у=x – 3 или y=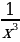

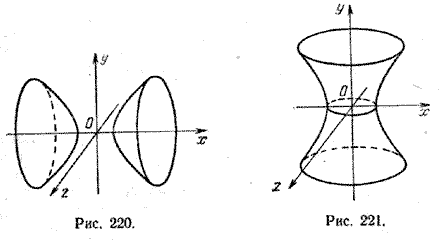
Гипербола часто встречается в природе.


Вращая гиперболу вокруг каждой из осей, получают два гиперболоида вращения – однополостной и двуполостной.
Выступление 2 группы:
«Функция вида y=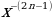 , где n – натуральное число, её свойства и график»
, где n – натуральное число, её свойства и график»
Рассмотрим функцию y=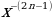 (где n – натуральное число) или y=
(где n – натуральное число) или y=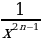
Свойства функции:
1.D(f): x(-∞;0)U(0;+∞).
2. Е(у)=(-∞;0)U(0;+∞).
3. Нечетная.
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 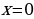 ; это симметричное множество.
; это симметричное множество.
Далее имеем 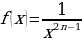 ,
,
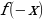 =
=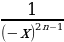 =
=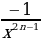 , таким образом,
, таким образом, 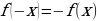 , а значит
, а значит 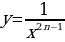 – нечетная функция.
– нечетная функция.
График данной функции симметричен относительно начала координат.
4. Убывает на промежутках (–∞; 0) и (0; +∞).
5. Не ограничена ни снизу, ни сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.
7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вниз при 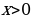 , выпукла вверх при
, выпукла вверх при 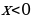 .
.
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).
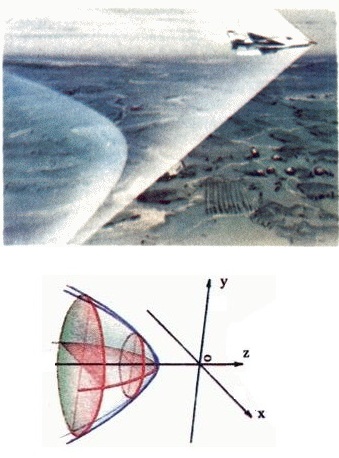
Во времена второй мировой войны гиперболы применялись для определения местоположения. На двух радиостанция одновременно испускалось два радиосигнала, человек определяющий своё местоположение расчитывал время между приходом каждого из этих дух сигналов, после чего строил на карте две гиперболы. Местом их пересечения и было его дислокация.
Это свойство используется в антеннах Кассегрена

Еще пример зона слышимости звука пролетающего самолета. Если самолет движется со сверхзвуковой скоростью, то в воздухе зона слышимости образует трехмерную поверхность – гиперболоид вращения.
Выступление 3 группы:
«Функции 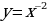 ,
, 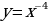 , их свойства и график»
, их свойства и график»
Рассмотрим функцию y=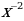 или у=
или у=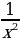
Свойства:
1.D(f): x (-∞;0)U(0;+∞).
2. Е(f): y0.
3. Четная
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 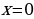 ; это симметричное множество.
; это симметричное множество.
Далее имеем 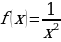 ,
,
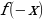 =
=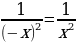 , таким образом,
, таким образом, 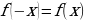 .
.
Значит (по определению) функция четная.
Тогда по свойству четной функции, чтобы построить график функции y=x-2, нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от оси ординат.
4. Убывает на интервале (0;+∞), возрастает на интервале (-∞;0).
Докажем это.
1 случай: х0.
Пусть 0x12, тогда 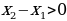 ,
, 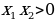 ,
, 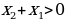 , значит
, значит 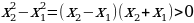 ,
, 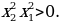 Имеем: у(x1)=
Имеем: у(x1)= 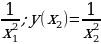 . Рассмотрим
. Рассмотрим 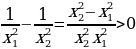 . Значит функция
. Значит функция 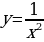 убывает при х0.
убывает при х0.
2 случай: х.
Пусть x1x2 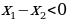 ,
, 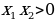 ,
,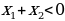 , значит
, значит 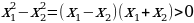 ,
, 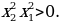 Имеем: у(x1)=
Имеем: у(x1)= 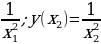 . Рассмотрим
. Рассмотрим 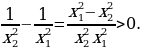 Значит функция
Значит функция 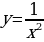 возрастает при х
возрастает при х
5. Ограничена снизу и не ограничена сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.
7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вниз и при  , и при
, и при  .
.
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).
График данной функции относится к видам гипербол.
Аналогичные свойства имеет функция у=x – 4 или 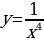

Выступление 4 группы:
«Функция вида y=x - 2n, где n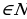 , её свойства и график»
, её свойства и график»
Рассмотрим функцию y=x - 2n, где n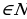 , или
, или 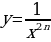
Свойства функции:
1.D(f): x (-∞;0)U(0;+∞).
2. Е(f): y0.
3. Четная.
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 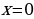 ; это симметричное множество.
; это симметричное множество.
Далее имеем 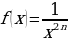 ,
,
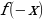 =
=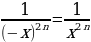 , таким образом,
, таким образом, 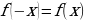 .
.
Значит (по определению) функция четная.
График симметричен относительно оси Оу
4. Убывает на интервале (0;+∞), возрастает на интервале (-∞;0).
5. Ограничена снизу и не ограничена сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.
7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вниз и при 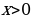 , и при
, и при  .
.
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).
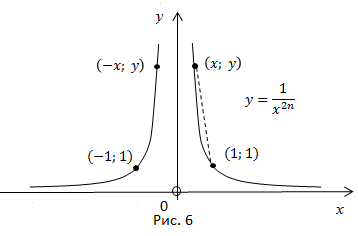
Каждая ветвь такой гиперболы проходит соответственно через точки: 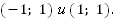



Не заполненная канва-таблица
| Функция | Область определения | Множество значений | Четность функции | Промежутки убывания и возрастания функции | Ограниченность функции | Наибольшие и наименьшие значения функции | Непрерывность функции | Выпуклость функции | Асимптоты | График функции |
| y=x-1 |
|
|
|
|
|
|
|
|
| 
|
| y=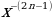 , где n , где n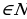
|
|
|
|
|
|
|
|
|
| 
|
| y=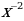
|
|
|
|
|
|
|
|
|
| 
|
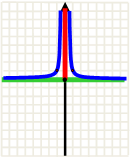
| y=x - 2n, где n
|
|
|
|
|
|
|
|
|
| 
|
Заполненная канва-таблица
| Функция | Область определения | Множество значений | Четность функции | Промежутки убывания и возрастания функции | Ограниченность функции | Наибольшие и наименьшие значения функции | Непрерывность функции | Выпуклость функции | Асимптоты | График функции |
| y=x-1 | (-∞;0)U (0;+∞) | (–∞; 0)U (0; +∞) | нечетная | убывает на (–∞; 0) и на (0; +∞) | не ограничена ни снизу, ни сверху | нет ни наибольшего, ни наименьшего значений | непрерывна на (-∞;0) и на (0;+∞) | выпукла вниз при 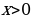 , выпукла вверх при , выпукла вверх при 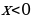 | у=0 – горизонтальная асимптота х=0 - вертикальная асимптота | 
|
| y=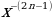 , где n – натуральное число , где n – натуральное число | (-∞;0)U (0;+∞) | (-∞;0)U (0;+∞) | нечетная | убывает на (-∞;0) и на (0;+∞) | не ограничена ни снизу, ни сверху | нет ни наибольшего, ни наименьшего значений | непрерывна на (-∞;0) и на (0;+∞) | выпукла вниз при 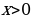 , выпукла вверх при , выпукла вверх при 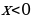 | у=0 – горизонтальная асимптота х=0 - вертикальная асимптота | 
|
| y=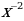
| (-∞;0)U (0;+∞) | y0 | четная | убывает на (0;+∞), возрастает на (-∞;0) | ограничена снизу и не ограничена сверху
| нет ни наибольшего, ни наименьшего значений | непрерывна на (-∞;0) и на (0;+∞) | выпукла вниз и при 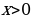 , и при , и при 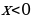 | у=0 – горизонтальная асимптота х=0 - вертикальная асимптота | 
|
| y=x - 2n, где n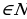
| (-∞;0)U (0;+∞) | y0 | четная | убывает на (0;+∞), возрастает на (-∞;0) | ограничена снизу и не ограничена сверху | нет ни наибольшего, ни наименьшего значений | непрерывна на (-∞;0) и на (0;+∞) | выпукла вниз и при 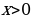 , и при , и при 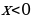 | у=0 – горизонтальная асимптота х=0 - вертикальная асимптота | 
|
Рефераты
1 группа
Функции у=x - 1 и у=x - 3, их свойства и графики
Рассмотрим функцию y=x-1 или 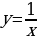 .
.
Свойства:
1.D(f): x 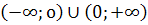 .
.
2. E(x)=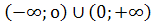 . При x 0 f (x) 0.
. При x 0 f (x) 0.
3. Нечетная.
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 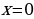 ; это симметричное множество.
; это симметричное множество.
Далее имеем 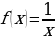 ,
,
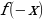 =
=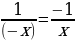 , таким образом,
, таким образом, 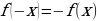 , а значит
, а значит 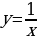 – нечетная функция.
– нечетная функция.
Тогда по свойству нечетной функции, чтобы построить график функции y=x-1, нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от начала координат.
4. Убывает на промежутках (–∞; 0) и (0; +∞).
Докажем это.
1 случай: х0.
Пусть 0x12, значит 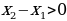 ,
, 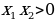 .
. Имеем: у(x1)=
Имеем: у(x1)= 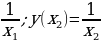 . Рассмотрим
. Рассмотрим 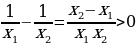 . Значит функция
. Значит функция 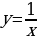 убывает при х0.
убывает при х0.
2 случай: х.
Пусть x1x2 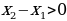 ,
, 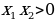 . Имеем: у(x1)=
. Имеем: у(x1)= 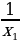 ;
;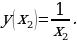 Рассмотрим
Рассмотрим 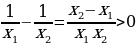 . Значит функция
. Значит функция 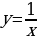 убывает при х
убывает при х
5. Не ограничена ни снизу, ни сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.
| x | 1 | 0,5 | -1 | -0,5 |
| y | 1 | 2 | -1 | -2 |

7.Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8.Выпукла вниз и при 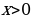 и при
и при 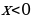 .
.
Прямые y = 0 и x = 0 являются асимптотами.
Графики функций вида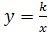 , где k
, где k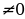 , в частности, график функции
, в частности, график функции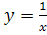 называются гиперболами.
называются гиперболами.
Рассмотрим функцию y=x-3 или 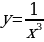 .
.
Свойства:
1.D(f): x 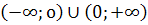 .
.
2. 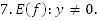
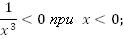
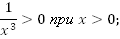
3. Нечетная
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 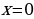 ; это симметричное множество.
; это симметричное множество.
Имеем 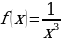 ,
,
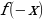 =
=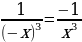 , таким образом,
, таким образом, 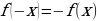 , а значит
, а значит 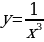 – нечетная функция.
– нечетная функция.
Тогда по свойству нечетной функции, чтобы построить график функции y=x-3, нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от начала координат.
4. Убывает на промежутках (–∞; 0) и (0; +∞).
Докажем это.
1 случай: х0.
Пусть 0x12, значит 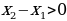 ,
, 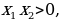
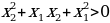 .
. Имеем: у(x1)=
Имеем: у(x1)= 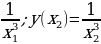 . Рассмотрим
. Рассмотрим 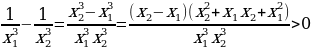 . Значит функция
. Значит функция 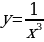 убывает при х0.
убывает при х0.
2 случай: х.
Пусть x1x2 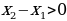 ,
, 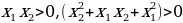 . Имеем:
. Имеем: 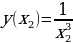 ; у(x1)=
; у(x1)= 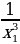 . Рассмотрим
. Рассмотрим 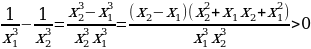 . Значит функция
. Значит функция 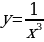 убывает при х
убывает при х
5. Функция не ограничена.
6. Не имеет ни наименьшего, ни наибольшего значений

7.Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8.Выпукла вниз и при  и при
и при  .
.
Прямые y = 0 и x = 0 являются асимптотами.
Гипербола часто встречается в природе.


Вращая гиперболу вокруг каждой из осей, получают два гиперболоида вращения – однополостной и двуполостной.


Задание 1: Найдите наибольшее и наименьшее значения функции y=x-3:
а) на отрезке [2; 5];
б) на луче [2; + ∞);
в) на отрезке [-5; -2].
Решение:
а) на отрезке [2;5]
y=x-3 убывает на промежутке (0; +∞)
yнаим = y(5)=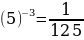 , yнаиб = y(2)=
, yнаиб = y(2)=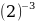 =
=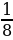
б) на луче [2; + ∞)
y=x-3 убывает на промежутке (0; +∞)
yнаим - не существует; yнаиб = y(2)=(2)-3 =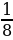
в) на отрезке [-5; -2]
y=x-3 убывает на промежутке (-∞;0)
yнаим - не существует; yнаиб = y(-2)=(-2)-3 =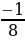
2 группа
Функция вида y=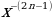 , где n – натуральное число, её свойства и график
, где n – натуральное число, её свойства и график
Рассмотрим функцию y=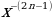 (где n – натуральное число) или y=
(где n – натуральное число) или y=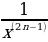
Свойства функции:
1.D(f): x(-∞;0)U(0;+∞).
2. Е(у)=(-∞;0)U(0;+∞).
3. Нечетная.
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 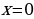 ; это симметричное множество.
; это симметричное множество.
Далее имеем 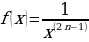 ,
,
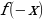 =
=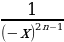 , таким образом,
, таким образом, 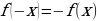 , а значит
, а значит 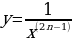 – нечетная функция.
– нечетная функция.
Тогда по свойству нечетной функции, чтобы построить график функции y=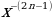 , нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от начала координат.
, нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от начала координат.
График данной функции симметричен относительно начала координат.
4. Убывает на промежутках (–∞; 0) и (0; +∞).
5. Не ограничена ни снизу, ни сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.
7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вверх при 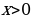 , выпукла вниз при
, выпукла вниз при 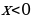 .
.
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).

Пример: y=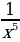
Свойства функции:
Рассмотрим функцию y=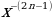 (где n – натуральное число) или y=
(где n – натуральное число) или y=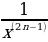
Свойства функции:
1.D(f): x(-∞;0)U(0;+∞).
2. Е(у)=(-∞;0)U(0;+∞).
3. Нечетная.
4. Убывает на промежутках (–∞; 0) и (0; +∞).
5. Не ограничена ни снизу, ни сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.
7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вверх при 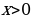 , выпукла вниз при
, выпукла вниз при 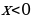 .
.
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).
| x | 0 | 0,8 | 1 | 2 |
| y | - | 3 | 1 | 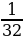
|
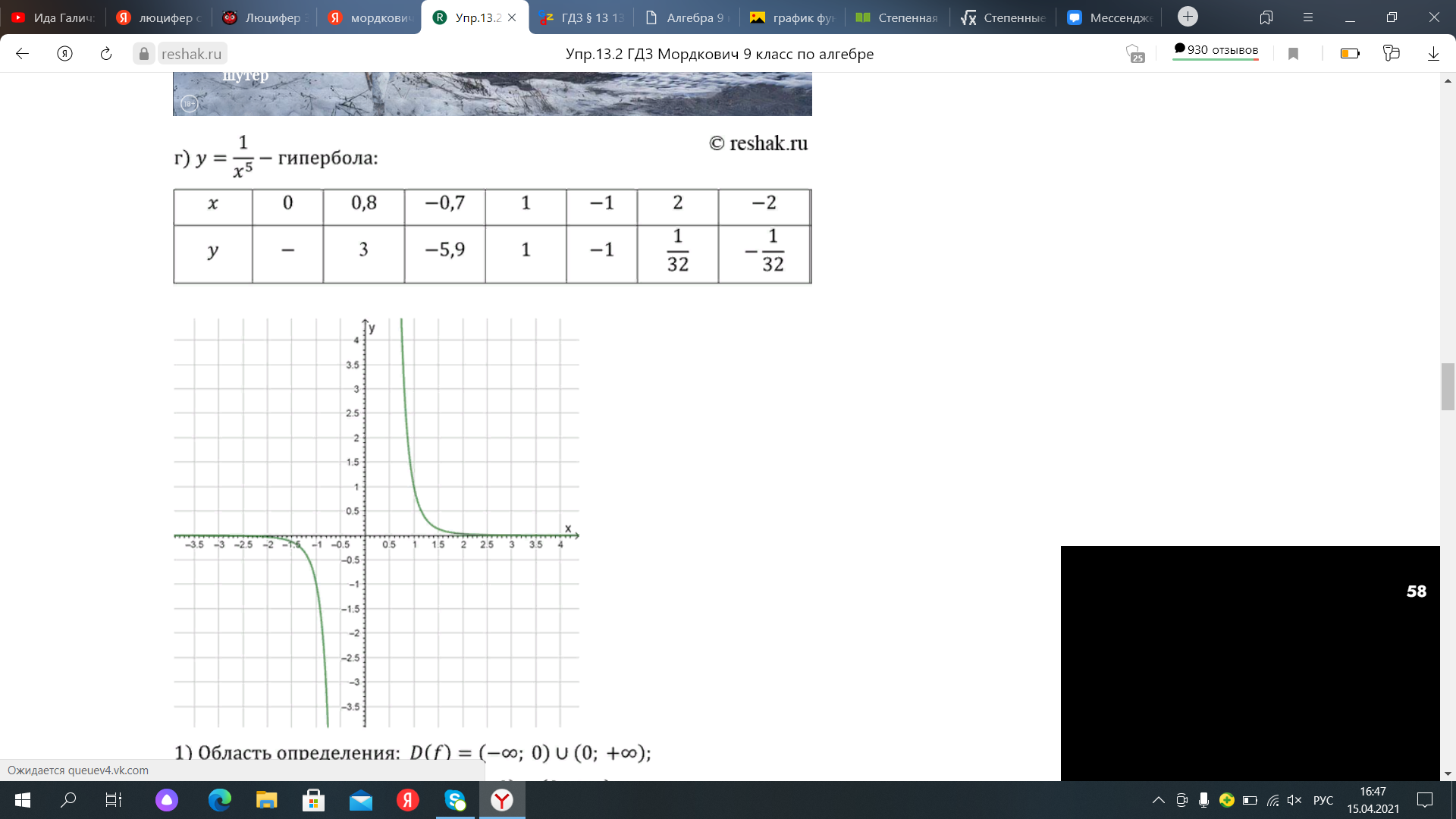
Во времена второй мировой войны гиперболы применялись для определения местоположения. На двух радиостанция одновременно испускалось два радиосигнала, человек определяющий своё местоположение расчитывал время между приходом каждого из этих дух сигналов, после чего строил на карте две гиперболы. Местом их пересечения и было его дислокация.
Это свойство используется в антеннах Кассегрена

Еще пример зона слышимости звука пролетающего самолета. Если самолет движется со сверхзвуковой скоростью, то в воздухе зона слышимости образует трехмерную поверхность – гиперболоид вращения.

Задание: Найдите наименьшее и наибольшее значения функции y=x-5
а) на отрезке [-2;-1]
б) на луче [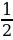 ; +)
; +)
Решение:
а) на отрезке [-2;-1]
y=x-5убывает на промежутке (–∞; 0)
yнаим=y(-1)=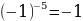 , yнаиб=y(-2)=
, yнаиб=y(-2)=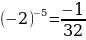
б) на луче [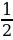 ; +)
; +)
y=x-5 убывает на промежутке (0; +∞)
yнаиб=y(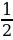 )=
)=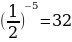 , yнаим-не существует
, yнаим-не существует
3 группа
Функции 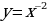 ,
, 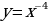 , их свойства и график.
, их свойства и график.
Рассмотрим функцию y=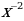 или у=
или у=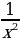
Свойства:
1.D(f): x (-∞;0)U(0;+∞).
2. Е(f): y0.
3. Четная
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 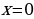 ; это симметричное множество.
; это симметричное множество.
Далее имеем 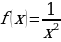 ,
,
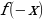 =
=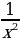 , таким образом,
, таким образом, 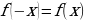 .
.
Значит (по определению) функция четная.
Тогда по свойству четной функции, чтобы построить график функции y=x-2, нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от оси ординат.
4. Убывает на интервале (0;+∞), возрастает на интервале (-∞;0).
Докажем это.
1 случай: х0.
Пусть 0x12, тогда 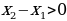 ,
, 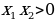 ,
, 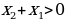 значит
значит 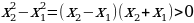 ,
, 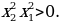 Имеем: у(x1)=
Имеем: у(x1)= 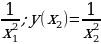 . Рассмотрим
. Рассмотрим 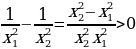 . Значит функция
. Значит функция 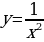 убывает при х0.
убывает при х0.
2 случай: х.
Пусть x1x2 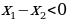 ,
, 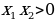 ,
,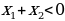 , значит
, значит 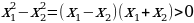 ,
, 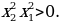 Имеем: у(x1)=
Имеем: у(x1)= 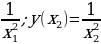 . Рассмотрим
. Рассмотрим 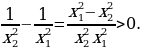 Значит функция
Значит функция 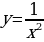 возрастает при х
возрастает при х
5. Ограничена снизу и не ограничена сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.

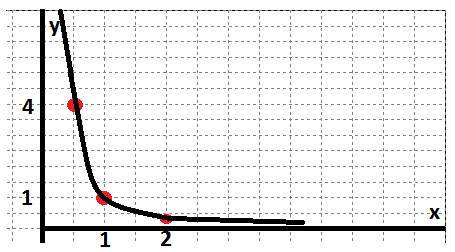
Воспользуемся свойством четности и отразим график относительно оси ординат.

7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вниз и при 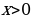 , и при
, и при 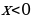 .
.
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).
График данной функции относится к видам гипербол.
y=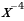
у=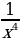
Исследуем на свойства:
1.D(f): x (-∞;0)U(0;+∞).
2. Е(f): y0.
3. Четная
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 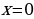 ; это симметричное множество.
; это симметричное множество.
Далее имеем 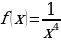 ,
,
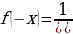 , таким образом,
, таким образом, 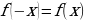 .
.
Значит (по определению) функция четная.
Тогда по свойству четной функции, чтобы построить график функции y=x-2, нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от оси ординат.
4. Убывает на интервале (0;+∞), возрастает на интервале (-∞;0).
Докажем это.
1 случай: х0.
Пусть 0x12, тогда значит 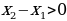 ,
, 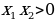 ,
, 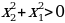 ,
, 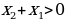 , значит
, значит 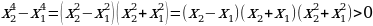 ,
, 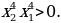 Имеем: у(x1)=
Имеем: у(x1)= 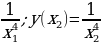 . Рассмотрим
. Рассмотрим 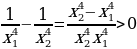 . Значит функция
. Значит функция 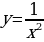 убывает при х0.
убывает при х0.
2 случай: х.
Пусть x1x2значит 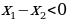 ,
, 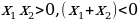 ,
, 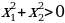 значит
значит 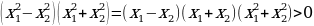 ,
, 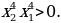 Имеем: у(x1)=
Имеем: у(x1)= 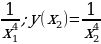 . Рассмотрим
. Рассмотрим 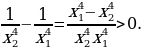 Значит функция
Значит функция 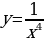 возрастает при х
возрастает при х
5. Ограничена снизу и не ограничена сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.

7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вниз и при 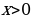 , и при
, и при 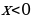 .
.
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).
График данной функции относится к видам гипербол.

Задание: Найдите наименьшее и наибольшее значения функции y=x-4
а) на отрезке [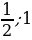 ]
]
б) на луче (-∞;-2]
Решение:
а) на отрезке [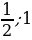 ]
]
y=x-4 убывает на интервале (0;+∞)
yнаим = y(1)=1-4=1, yнаиб = y(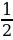 )=
)= =
=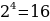
б) на луче (-∞;-2]
y=x-4 возрастает на интервале (-∞;0)
yнаим- не существует, yнаиб = y(-2)= =
=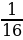
4 группа
Функция вида y=x - 2n, где n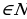 , её свойства и график
, её свойства и график
Рассмотрим функцию y=x - 2n, где n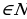 , или
, или 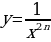
Свойства функции:
1.D(f): x (-∞;0)U(0;+∞).
2. Е(f): y0.
3. Четная.
Докажем это.
Заметим, что область определения функции – множество всех действительных чисел, за исключением 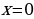 ; это симметричное множество.
; это симметричное множество.
Далее имеем 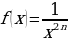 ,
,
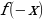 =
=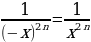 , таким образом,
, таким образом, 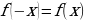 .
.
Значит (по определению) функция четная.
Тогда по свойству четной функции, чтобы построить график функции y=x - 2n, нужно построить график данной функции на открытом луче (0; +∞), а затем симметрично отразить его от оси ординат.
График симметричен относительно оси Оу
4. Убывает на интервале (0;+∞), возрастает на интервале (-∞;0).
5. Ограничена снизу и не ограничена сверху.
6. Не имеет ни наибольшего, ни наименьшего значений.
7. Непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
8. Выпукла вниз и при 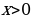 , и при
, и при 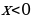 .
.
Прямые y = 0 и x = 0 являются её асимптотами (горизонтальной и вертикальной).

Каждая ветвь гиперболы проходит соответственно через точки: 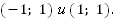
у=x – 6
у=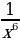
D(f)=(-∞;0) (0;+∞)
Множество значений: y0
Четная функция, т.к.  , график функции симметричен относительно оси ординат.
, график функции симметричен относительно оси ординат.
Убывает на луче (0;+∞) и возрастает на луче (-∞;0)
Ограничена снизу и не ограничена сверху.
Не имеет ни наибольшего, ни наименьшего значения.
Непрерывна на луче (-∞;0) и на луче (0;+∞) .
Выпукла вниз на луче (-∞;0) и на луче (0;+∞) .
Асимптоты: горизонтальная y=0 и вертикальная x=0.
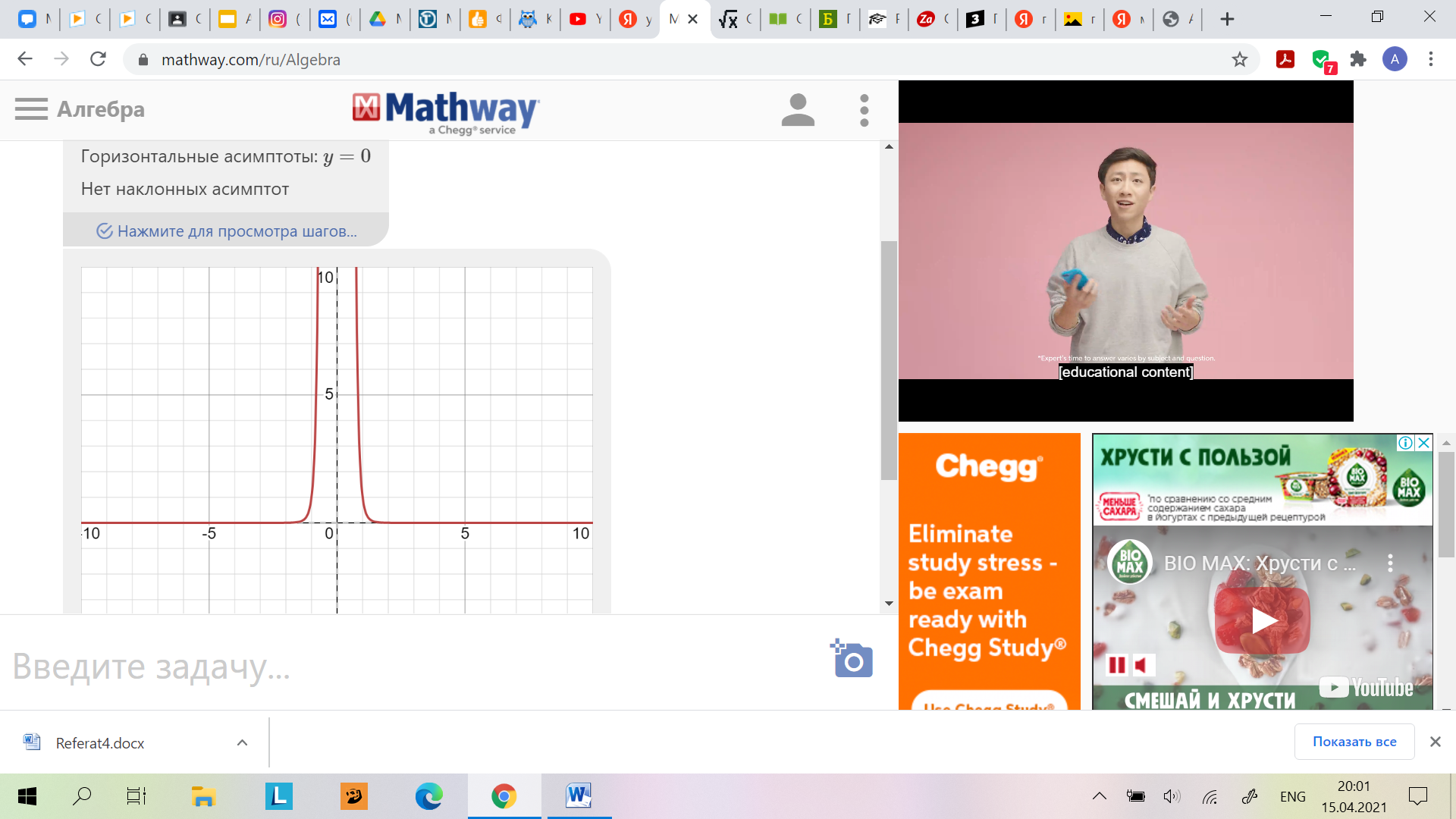


Задание: Найдите наименьшее и наибольшее значения функции y=x-6:
а) на отрезке [-3;-1];
б) на луче (-; -1];
в) на отрезке [1;3]
Решение:
а) на отрезке [-3;-1]
y=x-6возрастает на промежутке (–∞; 0)
yнаим = y(-3)=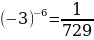 , yнаиб = y(-1)=
, yнаиб = y(-1)=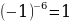
б) на луче (-; -1]
y=x-6возрастает на промежутке (–∞; 0)
yнаим = не существует, yнаиб = y(-1)=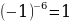
в) на отрезке [1;3]
y=x-6 убывает на луче (0;+∞)
yнаи? = ?, yнаи? = y(3)=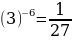







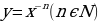 , их свойства и графики.
, их свойства и графики.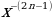 , где n-натуральное число, ее свойства и график»
, где n-натуральное число, ее свойства и график»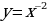 ,
, 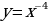 , их свойства и график»
, их свойства и график»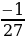
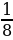
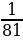
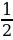 ;4]
;4]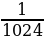 ; yнаиб - не существует
; yнаиб - не существует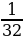
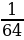 ; yнаиб=
; yнаиб= 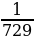
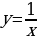 .
.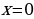 ; это симметричное множество.
; это симметричное множество. 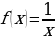 ,
,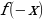 =
=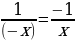 , таким образом,
, таким образом, 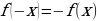 , а значит
, а значит 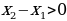 ,
, 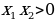 .
. Имеем: у(x1)=
Имеем: у(x1)= 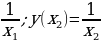 . Рассмотрим
. Рассмотрим 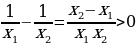 . Значит функция
. Значит функция 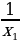 ;
;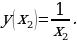 Рассмотрим
Рассмотрим 
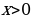 , выпукла вверх при
, выпукла вверх при 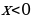 .
.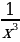




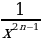
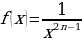 ,
,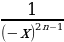 =
=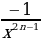 , таким образом,
, таким образом, 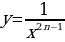 – нечетная функция.
– нечетная функция.


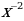 или у=
или у=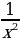
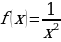 ,
,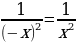 , таким образом,
, таким образом, 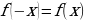 .
.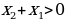 , значит
, значит 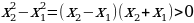 ,
, 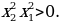 Имеем: у(x1)=
Имеем: у(x1)= 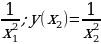 . Рассмотрим
. Рассмотрим 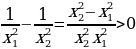 . Значит функция
. Значит функция 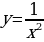 убывает при х0.
убывает при х0.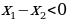 ,
, 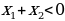 , значит
, значит 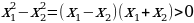 ,
, 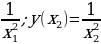 . Рассмотрим
. Рассмотрим 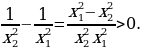 Значит функция
Значит функция 
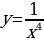



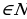 , её свойства и график»
, её свойства и график»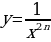
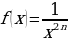 ,
,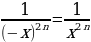 , таким образом,
, таким образом, 







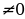 , в частности, график функции
, в частности, график функции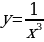 .
.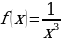 ,
,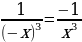 , таким образом,
, таким образом, 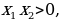
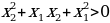 .
.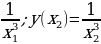 . Рассмотрим
. Рассмотрим 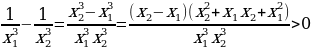 . Значит функция
. Значит функция 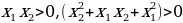 . Имеем:
. Имеем: 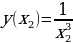 ; у(x1)=
; у(x1)= 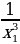 . Рассмотрим
. Рассмотрим 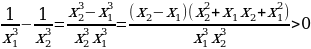 . Значит функция
. Значит функция 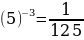 , yнаиб = y(2)=
, yнаиб = y(2)=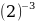 =
=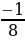
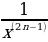
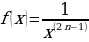 ,
,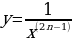 – нечетная функция.
– нечетная функция.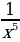

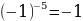 , yнаиб=y(-2)=
, yнаиб=y(-2)=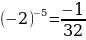
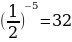 , yнаим-не существует
, yнаим-не существует
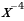
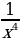
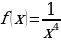 ,
,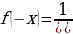 , таким образом,
, таким образом, 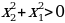 ,
, 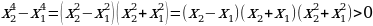 ,
, 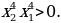 Имеем: у(x1)=
Имеем: у(x1)= 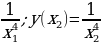 . Рассмотрим
. Рассмотрим 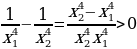 . Значит функция
. Значит функция 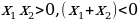 ,
, 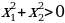 значит
значит 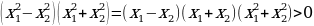 ,
, 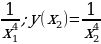 . Рассмотрим
. Рассмотрим 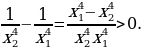 Значит функция
Значит функция 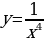 возрастает при х
возрастает при х

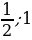 ]
] =
=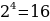
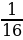
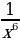
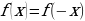 , график функции симметричен относительно оси ординат.
, график функции симметричен относительно оси ординат.

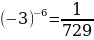 , yнаиб = y(-1)=
, yнаиб = y(-1)=