Функции в окружающем мире

МОУ «Средняя общеобразовательная школа с углублённым изучением отдельных предметов №30»

Математические функции в окружающем мире

Автор: Диков Срегей, 9А класс

Руководитель работы: Зобнина Наталья Александровна, учитель математики

ГО САРАНСК-2016

Цель: выявить и изучить области применения функции в окружающей жизни, установить связь математических функций с другими науками, рассмотреть прикладные задачи функциональной зависимости.

Задачи:

1.Подобрать и проанализировать соответствующую литературу;

2.Рассмотреть применение функции в точных и естественных науках;

3.Рассмотреть применение функции в истории и филологии;

4.Показать применение функции в природе, науке и жизни человека.

5.Установить функциональные зависимости на примерах окружающего мира;

6 . Расширение кругозора учащихся и повышение уровня знаний по предмету.

Гипотеза: функциональные зависимости существуют во всех сферах жизни человека.

Объект исследования: Области применений математических функций.

Предмет исследования: Функциональные зависимости в окружающей жизни.

Методы исследования:

- теоретический;

- эмпирический.

Практическая значимость проекта. Работа позволяет развивать интерес школьников к урокам математики, убеждает в высокой практической значимости математической науки, формирует представление о взаимосвязи математики с объектами реального мира, убеждает в необходимости применять полученные знания на практике.

• История развития понятия функции.
• История развития понятия функции.

С древнейших времен до XVII века.

Аналитическое определение функции

(XVII - начало XIX века).

Само слово «функция» (от латинского functio -совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673г. в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати ввел с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины «переменная» и «константа». В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой. Это так называемая аналитическая точка зрения на понятие функции.

Идея соответствия (XIX век).

При любом геометрическом преобразовании мы имеем дело с функцией. Другими синонимами термина «функция» в различных отделах математики являются: соответствие, отображение, оператор, функционал и др.

Дальнейшее развитие понятия функции

(XX век - ...).

Необходимость дальнейшего расширения понятия функции стала особенно острой после выхода в свет в 1930 году книги «Основы квантовой механики» Поля Дирака, крупнейшего английского физика, одного из основателей квантовой механики. Дирак ввел так называемую дельта-функцию, которая выходила далеко за рамки классического определения функции.

Функции в школьной программе.

• 7 класс-Линейная функция: у=х, у=кх+b;
• 8класс- Квадратичная функция:у=кх 2 , у=ах 2 +вх+с;
• 9 класс- Степенная функция: у=х n , дробно-линейная:y= ;
• 10-11класс-Показательная, логарифмическая, тригонометрические функции: у=а х , у=log a x, у=sinx, y=cosx.

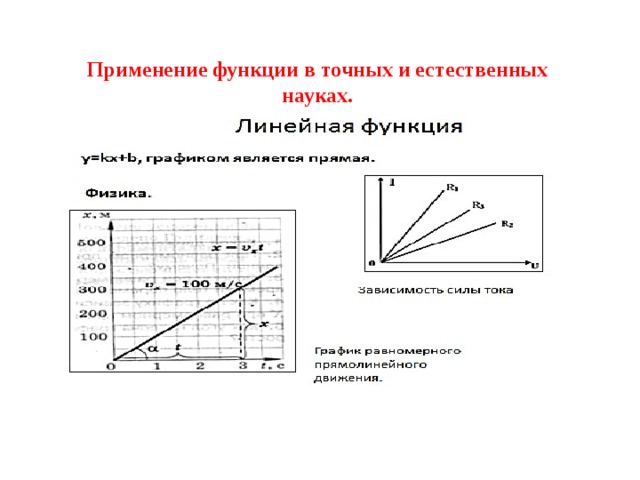
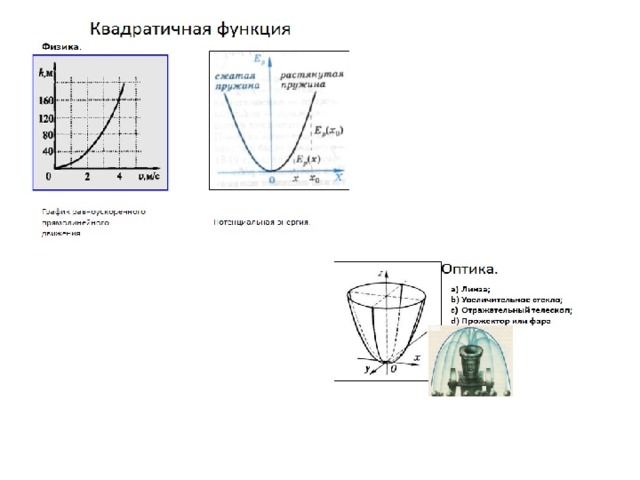
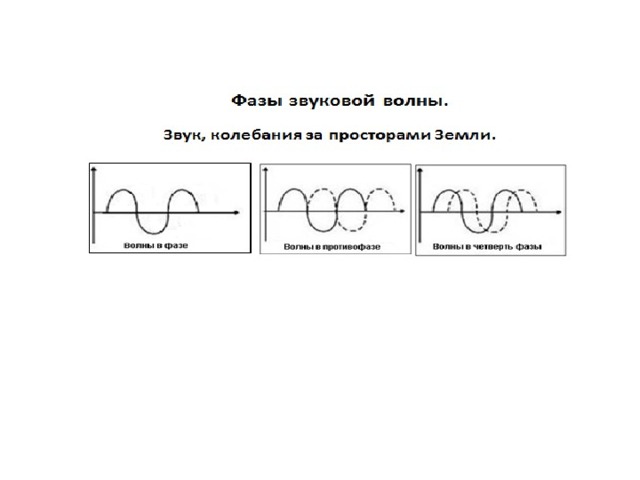
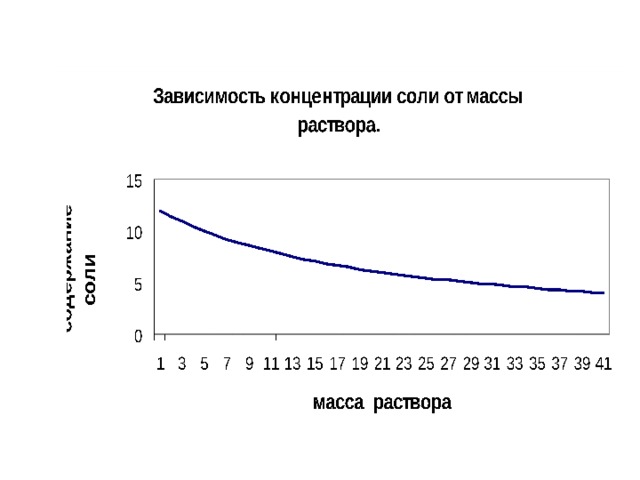
Применение функции в точных и естественных науках.

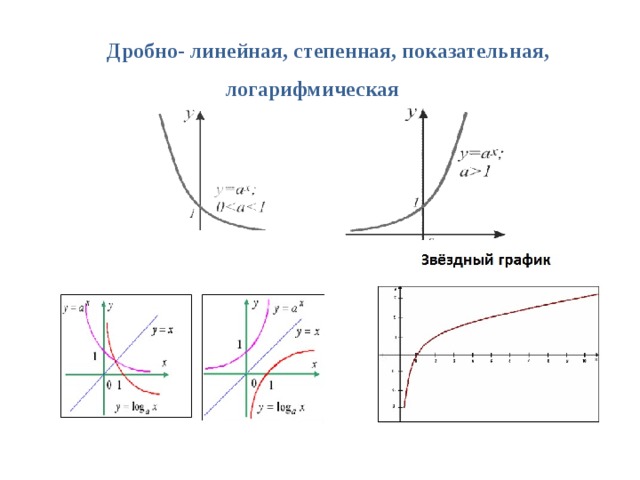
Дробно- линейная, степенная, показательная, логарифмическая

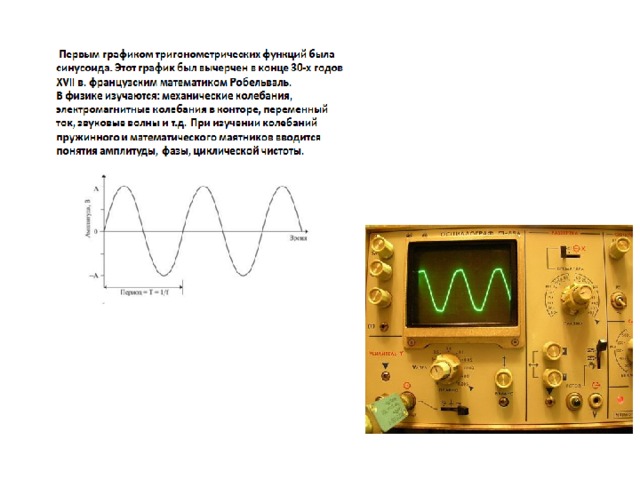
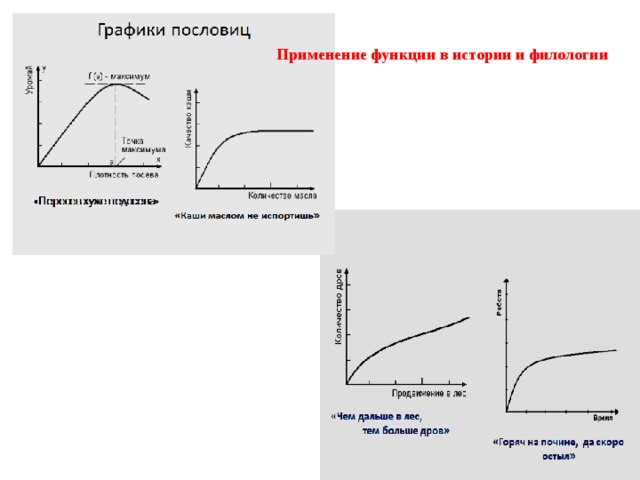
Применение функции в истории и филологии

Применение функции в жизни человека

«График информационного бума»

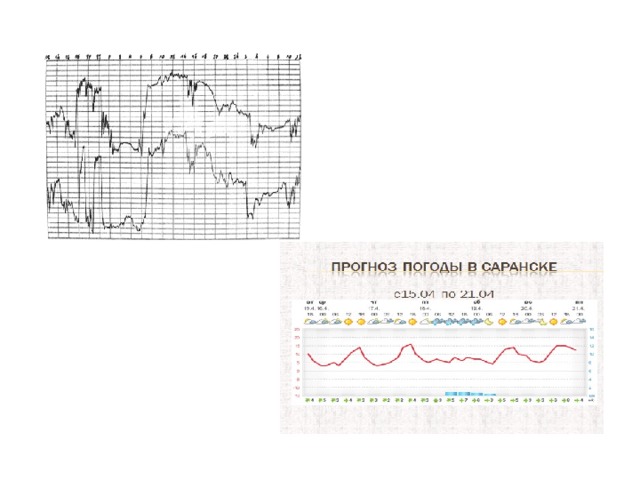
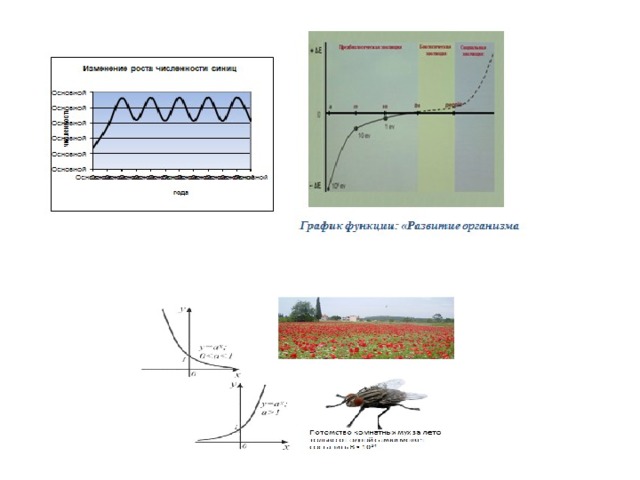
Функции в природе

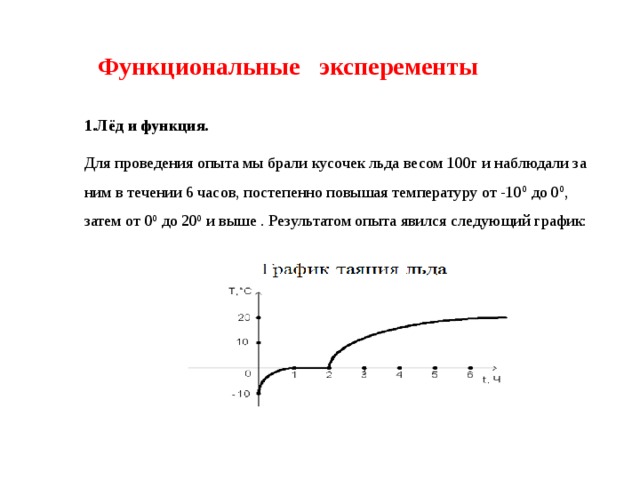
Функциональные эксперементы

1.Лёд и функция.

Для проведения опыта мы брали кусочек льда весом 100г и наблюдали за ним в течении 6 часов, постепенно повышая температуру от -10 0 до 0 0 , затем от 0 0 до 20 0 и выше . Результатом опыта явился следующий график:

Рыбы и математика

В результате наблюдений за аквариумными рыбами мы установили, что при плавании тело рыбы принимает форму кривой, которая напоминает график функции кубической параболы:

Летающая парабола

Выводы

  1. Математические функции являются одним из основных понятий в различных областях науки и техники.

2 .Математическое понятие функции широко используется в описании и изучении процессов и явлений реального мира.

3 .Широкое развитие физики, химии, биологии, авиации, сотовой связи и вообще техники было бы невозможным без понятия функции.

4. Функциональные зависимости присутствуют во всех сферах жизни человека.

5. Работа позволяет развивать интерес школьников к урокам математики, убеждает в высокой практической значимости математической науки, формирует представление о взаимосвязи математики с объектами реального мира, убеждает в необходимости применять полученные знания на практике.

Заключение

Изучая и анализируя области применения и взаимосвязь математических функций не только с естественными, но и гуманитарными науками, мы решили поставленные ранее задачи, а значит, добились цели нашего проекта.

Мы убедились в том, что функция является неотъемлемой частью нашей жизни и наук в целом, так как функциональные зависимости, действительно, существуют во всех сферах жизни человека.

СПАСИБО ЗА ВНИМАНИЕ !