МБОУ СОШ № 129
Тел ОУ: 8-(987) 477-12-24
Тема: «Функция у = cos x, ее свойства и график»
Автор: Чугаева Олеся Алексеевна
Должность: учитель математики
Домашний адрес: г. Уфа, ул Ушакова 90/1, (8347) 263-04-95
Уфа – 2016
Тема урока: Функция у = cos x, ее свойства и график.
Математика (10 класс)
Учебник: алгебра и начала анализа 10-11 А. Г. Мордкович
Учитель: Чугаева Олеся Алексеевна, МБОУ Школа № 129.
Тип урока: "открытие" нового знания.
Основные цели: формировать способность построения нового понятия и нового алгоритма, на примере функции у= sin x; повторить формулы приведения значения тригонометрических функций, повторить свойства и график функции у=sin x, познакомить учащихся с функцией y = cos x, рассмотреть график функции y = cos x и сформулировать ее свойства. Развивать умения, анализировать, применять имеющие знания у учащихся в изменённой ситуации.
Ход урока.
Самоопределение к деятельности (орг. момент).
Цель: включение учащихся в деятельность на личностно- значимом уровне.
«Хочу, потому что могу».
Время 1-2 минуты:
– Здравствуйте, ребята! Вспомните, какие темы были на прошлых уроках? (Мы рассматривали формулы приведения, изучили функцию у=sin x, рассмотрели ее свойства и график.)
– Как называется, глава, в которую входят названные темы? (Тригонометрия. Тригонометрические функции.)
– Что изучает тригонометрия ( раздел математики, изучающий тригонометрические функции и их применение к решению задач)
– Хорошо! Сегодня мы продолжим заниматься изучением тригонометрических функций, познакомимся с функцией y = cos x, рассмотрим график функции y = cos x и сформулируем ее свойства.
II. Актуализация знаний и фиксация затруднения в деятельности.
Цель: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося.
Время 4-5 минут;
Расставьте в порядке возрастания: cos 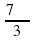 , tg
, tg 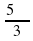 , sin
, sin 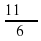 . (Через некоторое время, один из учащихся приглашается к доске, записывает решение и ответ)
. (Через некоторое время, один из учащихся приглашается к доске, записывает решение и ответ)
Решение:
cos 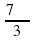 = cos (
= cos (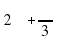 ) = cos
) = cos 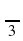 =
= 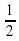
tg 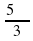 = tg (
= tg (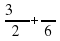 ) = - ctg
) = - ctg 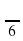 = -
= - 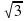
sin 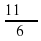 = sin (
= sin (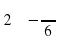 ) = - sin
) = - sin 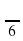 = -
= - 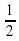
Ответ: tg 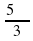 , sin
, sin 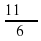 , cos
, cos 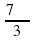 .
.
Вопросы классу:
-Ребята, что помогло нам, решить эту задачу?
-Использование формул приведения.
-А, могли бы мы, решить задачу не используя формулы приведения?
-Да, но формулы приведения тригонометрических функций упрощают вид формул и помогают совершать преобразования, приводящие к более простым выражениям.
Или - Формулы приведения, дают возможность находить численные значения тригонометрических функций углов, превышающих 90°.
-Ребята, а помните ли вы, с графиком какой функции мы познакомились с вами на прошлом уроке?
С графиком функции у=sin х.
Как называют линию, которая служит графиком функции y=sin х?
Линию которая служит графиком y=sin x, называют синусоидой.
Синусоида - плоская прямая, изображающая изменения синуса в зависимости от изменения угла.
А знаете ли вы что, если взять свечку, и обернуть её несколько раз листом бумаги, а затем перерезать её наклонно ножом, то разняв обе половины свечи и развернув бумагу, получим кривую линию которую называют - СИНУСОИДОЙ. Наиболее часто синусоида встречается в графиках(колебание груза на пружине, колебание маятника, колебание переменного тока)
Давайте посмотрим, ролик который называется «Колбасная синусоида»(на мультимедийном проекторе)
А теперь, я предлагаю вам записать свойства функции y=sin x и самим построить её график используя ее свойства.
Ученик записывает свойства и строит график.
D (f) = (- 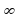 ; +
; + 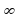 )
)
y=sin x-нечётная функция так как y(-x)=sin(-x)=-sin x=-y(x)
Функция y=sin x возрастает на любом отрезке 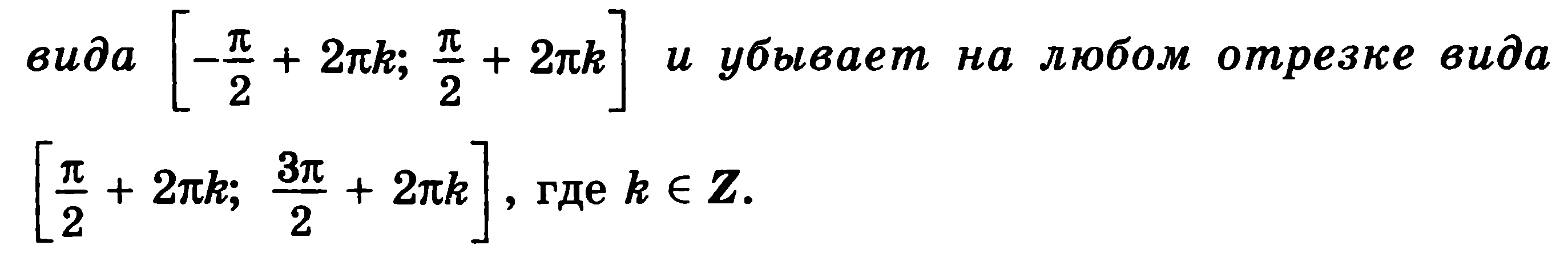
4. Функция y=sin x ограничена сверху и снизу -1 5. y наименьшее = -1, y наибольшее=1
6. y=sin x – непрерывная функция
7. Е(y) = [ - 1;1]
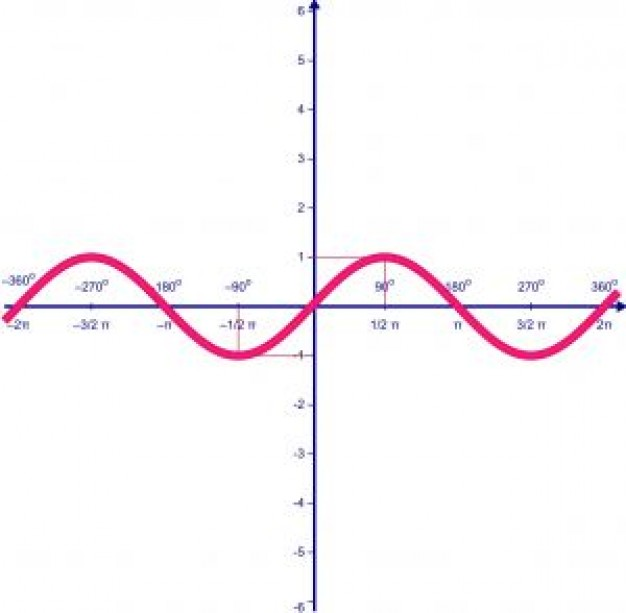
Скажите ребята, как вы думаете, какой из русских пословиц наиболее соответствует график функции y=sin x и почему?
1.Чем дальше в лес, тем больше дров.
2.Дальше кумы, меньше греха.
3.Кашу маслом не испортишь.
4.Выше меры конь не скачет.
5.Пересев хуже недосева.
ОТВЕТ ученика: №4, у графика функции у=sin x, тоже есть своя мера, выше которой волна синусоиды не поднимется. В этом одно из 2-х свойств точной верхней грани – 1. Но есть у значения Sin x и точная нижняя грань – минус 1.
Постановка учебной задачи.
Предложенное задание может у многих учащихся вызвать затруднение, т.к. раньше они не сталкивались с подобными задачами.
– Почему задача вызвала затруднение у многих ребят? (Мы раньше не решали такие задачи).
– На прошлых уроках мы уже строили график одной из тригонометрических функций, чем эта задача отличается от тех, которые мы решали раньше? (В этой задачи появились новая функция соs x.).
– Сформулируйте цель урока? (Научиться строить график функции у= соs x).
– Какова тема урока? (Функция y= cos x, ее свойства и график).
«Открытие нового знания» (построение проекта выхода из затруднения).
Как вы думаете, а как изменится график функции y = sin x, если функция задана в виде: y = sin (x+ П/2) ?
Ученик. Нужно построить график функции y = sin x и сдвинуть на П/2 относительно оси Х влево.
Ученик. А если, воспользоваться формулой приведения, то мы получим график функции у=cos x !!!
Молодцы, ребята. Я предлагаю вам, построить график функции y=cos x и по графику записать свойства графика этой функции.
V. Первичное закрепление во внешней речи.
Ученик у доски выполняет построение проговаривая решение.
Другой ученик и записывает свойства функции используя график.
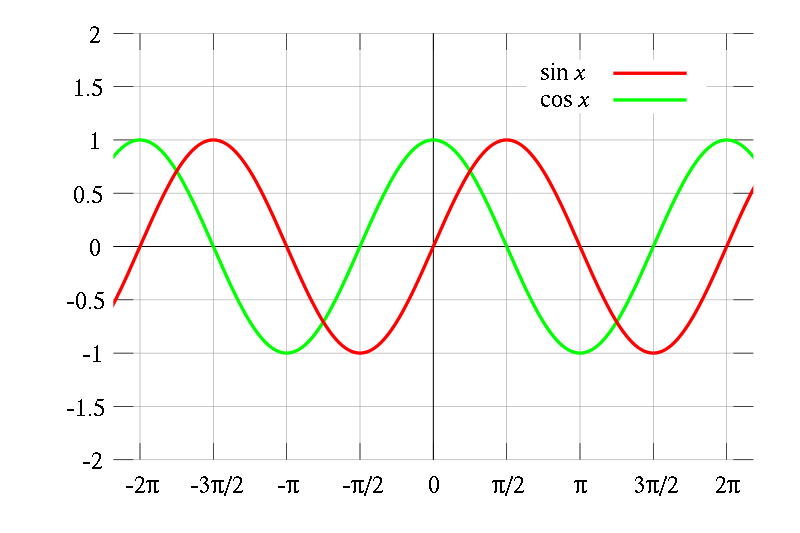
1.D(f) = (- 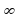 ; +
; + 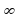 )
)
2. y = cos x – четная функция, так как y(-x)=cos(-x)=cos x=y(x)
3. y=cos x убывает [1;П], возрастает [П;2П]
4. функция ограничена сверху и снизу -1 5. y наименьшее = -1, y наибольшее = 1
6. y = cos x – непрерывная функция
7. E(y) = [ - 1 ; 1 ]
VI. Самостоятельная работа с самопроверкой по эталону. Самоанализ и
самоконтроль.
Цель: каждый для себя должен сделать вывод о том, что он уже умеет.
Время 4-5 минут;
Я предлагаю вам выполнить самостоятельно, по вариантам следующие примеры:
1 вариант: 2 вариант:
VII. Включение нового знания в систему знаний и повторение.
Пример: Решить графически уравнения а) sin x – x = 0
Х = 0
Ответ: 0.
б) cos x – 2 x = 1.
Первое уравнение решает ученик, второе уравнение помогает выполнить учитель.
VIII. Рефлексия деятельности (итог урока).
Цель: осознание учащимися своей УД (учебной деятельности), самооценка результатов деятельности своей и всего класса.
Время 2-3 минуты;
– С какой функцией мы познакомились сегодня на уроке? (Сегодня на нашем уроке мы познакомились с функцией у = соs x, ее графиком и свойствами).
– Что помогло нам при построении графика функции у= соs x? (Формулы приведения).
– Что мы повторили сегодня? (обобщили и закрепили ваши знания, умения и навыки в работе с формулами приведения; тригонометрическими функциями y= cos x, y = sin x; повторили свойства функции у= sin x; строили графики функций; решали уравнение графическим способом).
– Проанализируйте свою работу на уроке.
Д/з: Придумать два тригонометрических уравнения и решить их графическим способом.
Используемая литература:
Учебник по алгебре и началам анализа 10-11 А. Г. Мордкович 2009 г.
http://images.yandex.ru/yandsearch (рисунки графиков)
Пословицы http://www.konokrad.ru/poslovica/pro-konei/26-vishe-meri-i-kon-ne-skachet.
http://pikabu.ru/story/kolbasnaya_sinusoida_305798 ролик «Колбасная синусоида»






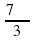 , tg
, tg 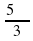 , sin
, sin 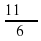 . (Через некоторое время, один из учащихся приглашается к доске, записывает решение и ответ)
. (Через некоторое время, один из учащихся приглашается к доске, записывает решение и ответ)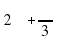 ) = cos
) = cos 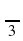 =
= 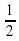
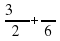 ) = - ctg
) = - ctg 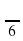 = -
= - 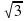
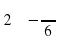 ) = - sin
) = - sin 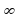 ; +
; +