Тема урока: Функции у=|x| и ей график.
Тип урока: изучение и закрепление новых знаний.
Цели урока:
Образовательные: познакомить учащихся с функцией у=|x|, её свойствами, графиком ; освоить метод построения графиков функций, содержащих знак модуль, сумму нескольких модулей, отработать еще раз прием переноса графика функции вдоль осей Ох и Оу.
Развивающие: развитие зрительной памяти, развитие математически грамотной речи, логического и творческого мышления, сознательного восприятия учебного материала, формирование навыков самостоятельной деятельности, выработки внимания, развивать умения применять знания на практике.
Воспитательные: воспитание познавательной активности, культуры общения, культуры диалога.
Структура урока:
Организационный момент.
Актуализация знаний.
Сообщение темы и целей урока.
Объяснение нового материала.
Применение знаний, умений и навыков в ходе построения графика функции.
Самостоятельная работа.
Подведение итогов.
Информация о домашнем задании.
1.Организационный момент.
2.Актуализация знаний учащихся.
Для того чтобы успешно справиться с поставленными целями урока, нам необходимо вспомнить некоторый теоретический материал:
Вопрос: Дайте определение линейной функции.
Ответ: Функция вида y=kx+b, где k и b – данные числа, называют линейной функцией.
Вопрос: Какова область определения линейной функции?
Ответ: Линейная функция определена на множестве действительных чисел, т.е. при 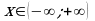 .
.
Вопрос: Что является графиком функции? (слайд 3)
Ответ: Графиком линейной функции y=kx+b является множество точек координатной плоскости xOy с координатами (х, kx+b), где х любое действительное число.
Или
Графиком линейной функции y=kx+b является прямая, пересекающая ось ординат в точке (0; b) , параллельная прямой  y=kx.
y=kx.
Или
Графиком линейной функции y=kx+b является прямая, проходящая через две точки (0; b) и (1, k+b).
Вопрос: Какой геометрический смысл имеют числа k и b для линейной функции y=kx+b?
Ответ: коэффициент k называют угловым коэффициентом прямой, если k0, то функция возрастает, если k, то функция убывает. Число b есть ордината точки пересечения прямой с осью у.
Вопрос:

Ответ:
а) график функции получим из графика функции у=3х параллельным переносом на 2 единицы влево;
б) график функции получим из графика функции у=3х параллельным переносом на 4 единицы вправо;
в) график функции получим из графика функции у=3х параллельным переносом на 3 единицы вверх;
г) график функции получим из графика функции у=3х параллельным переносом на 3 единицы вниз;
д) график функции получим из графика функции у=3х параллельным переносом на 4 единицы вправо и на 2 единицы вверх.
Давайте вспомним определение модуля.
3.Сообщение темы и целей урока.
Тема сегодняшнего урока: Функции у=|x| и ей график. Сегодня на уроке мы познакомимся с этой функцией, ее свойствами, графиком, освоим метод построения графиков функций содержащих знак модуль, сумму нескольких модулей, отработаем еще раз прием переноса графика функции вдоль осей координат.
4. Объяснение нового материала
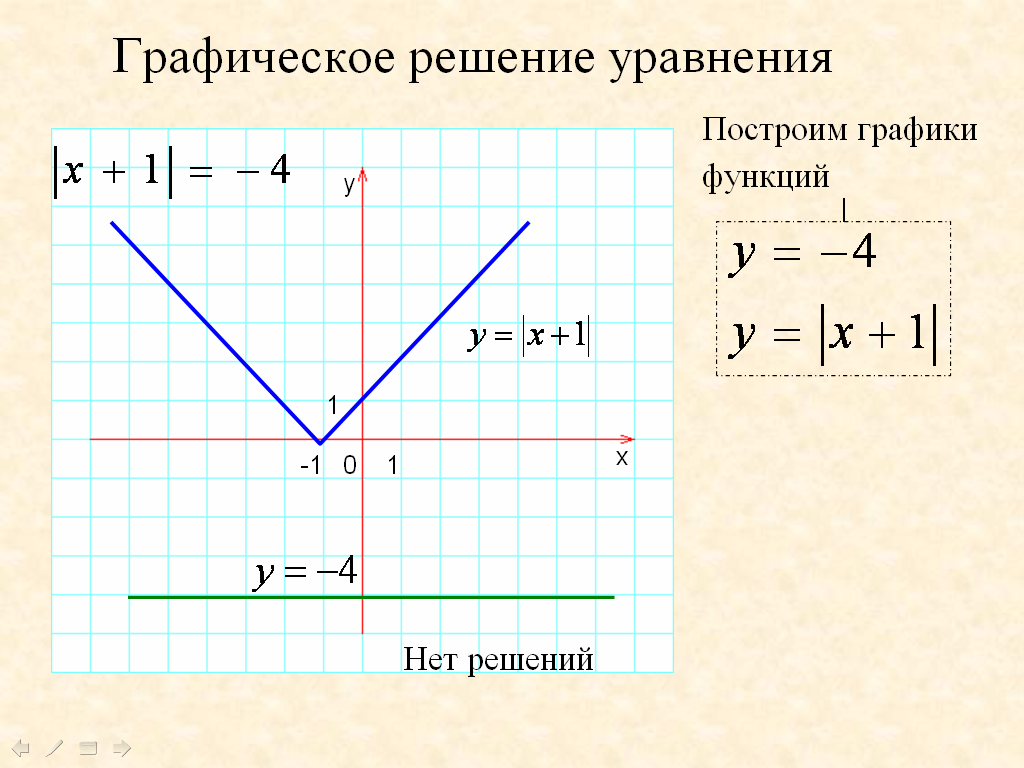
Рассмотрим функцию у=|x|
Еще раз вспомним определение модуля числа х.
|x|=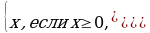
Поэтому можно записать у= 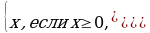
Ребята, наша задача, определить, что будет являться графиком этой функции. Мы видим, что числовая прямая Ох, разделена на интервал 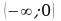 и полуинтервал
и полуинтервал  , т.е. при
, т.е. при 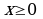 это биссектриса 1 координатной четверти, а при
это биссектриса 1 координатной четверти, а при 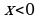 - второй. Итак, график функции у=|x| выглядит следующим образом.
- второй. Итак, график функции у=|x| выглядит следующим образом.
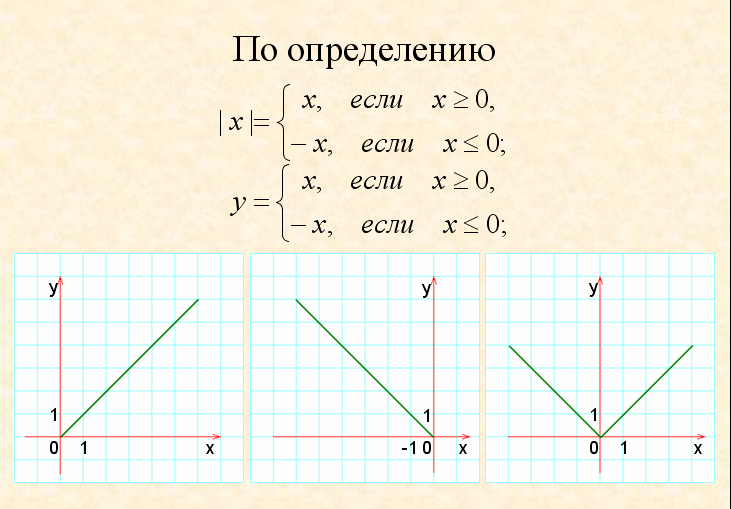
Итак, график функции выглядит так: (слайд 8)
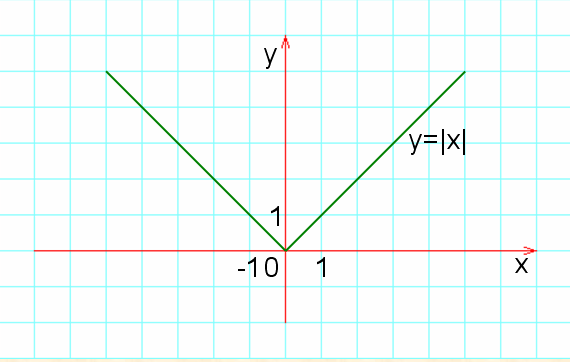
Ребята, кто может перечислить свойства этой функции, используя график? (слайд 9)

4.Применение знаний, умений и навыков в ходе построения графика
функции
Ребята, мы рассмотрели функцию у=|x|, ее свойства, график, теперь наша задача научиться строить график линейной функции, содержащей знак модуль.
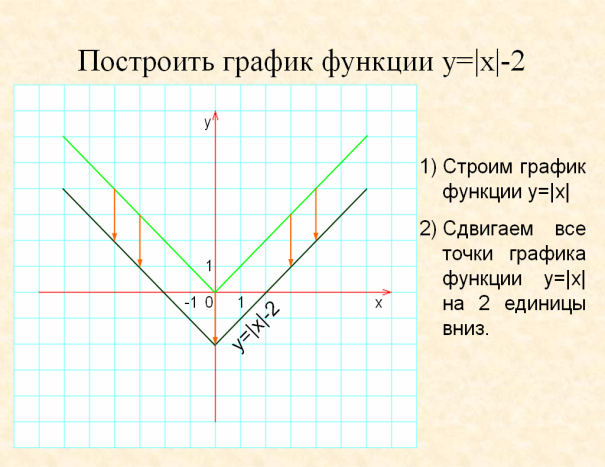
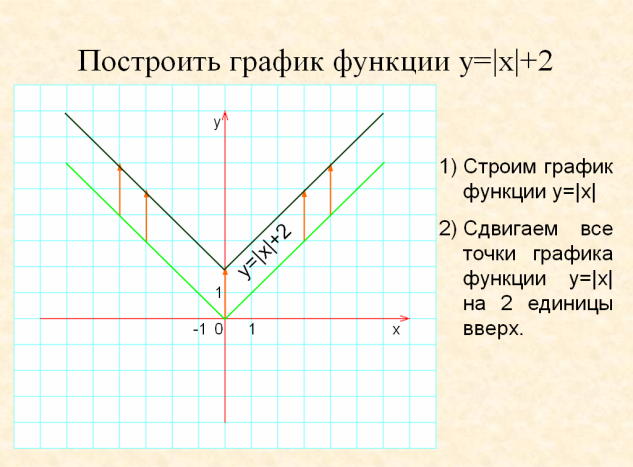

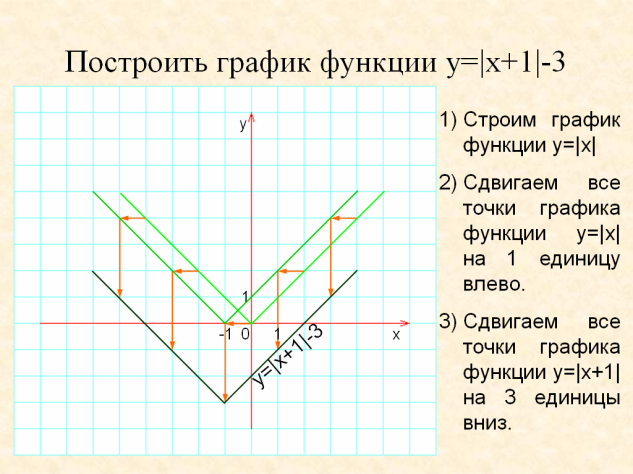
Следующее задание.
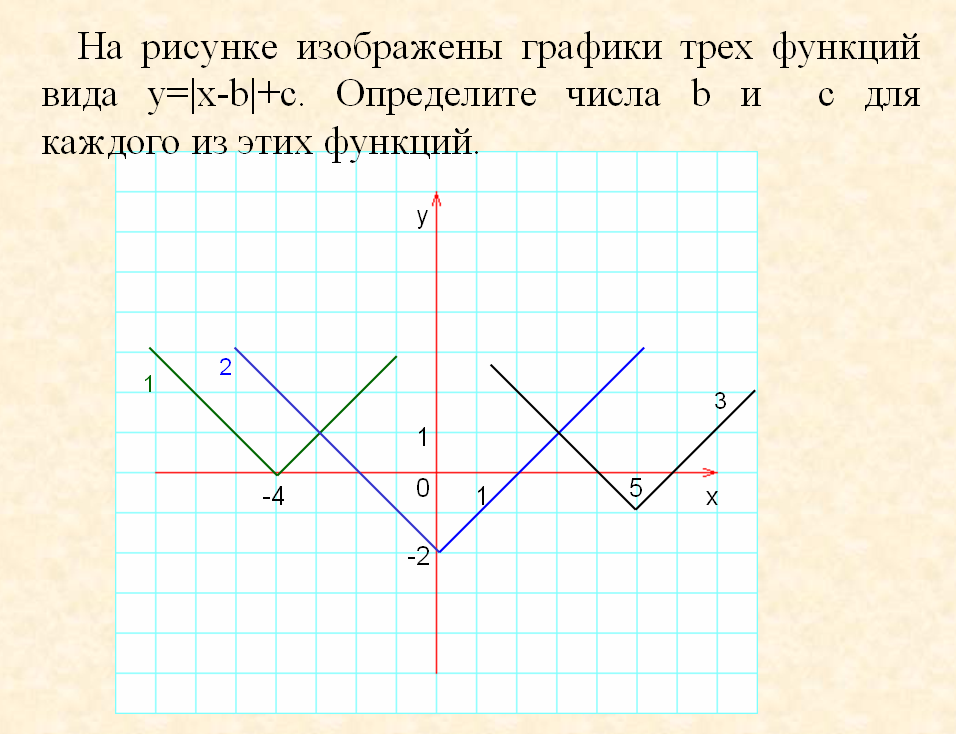
а) График функции получен из графика функции у=|х| параллельным переносом влево на 4 единицы и, значит, является графиком функции у =| x-(-4)|, т.е. b=-4, c=0.
б) График функции получен из графика функции у=|х| параллельным переносом вниз на 2 единицы и, значит, является графиком функции у=|x|-2, т.е. b=0, c=-2.
в) График функции получен из графика функции у=|х| параллельным переносом вправо на 6 единиц и вниз на 1 единицу, и, значит, является графиком функции у=|x-6| -1, т.е. b=6, c=-1.
Сейчас, ребята, вы будете работать на ПК в программе «Живая геометрия» У каждого из вас заданная функция, графики, которых вы должны построить (д.м. с.р.16 зад.№1 по вариантам).
1 вариант 2 вариант
Построить график функции
а)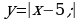 б)
б)  а)
а) 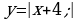 б)
б) 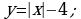
в) 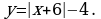 в)
в) 
С помощью сети, выполненные задания проецируются на экран. Так с помощью учащихся происходит проверка.
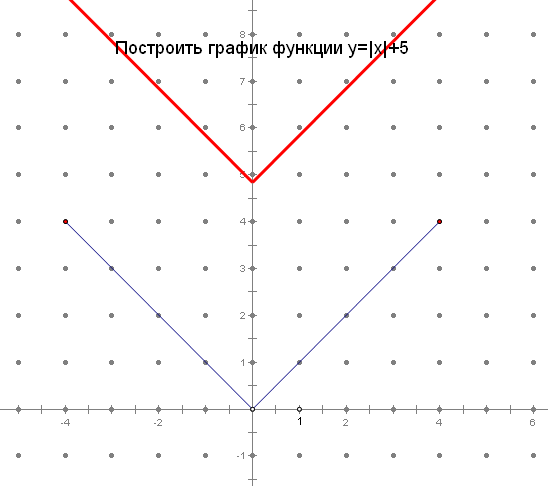
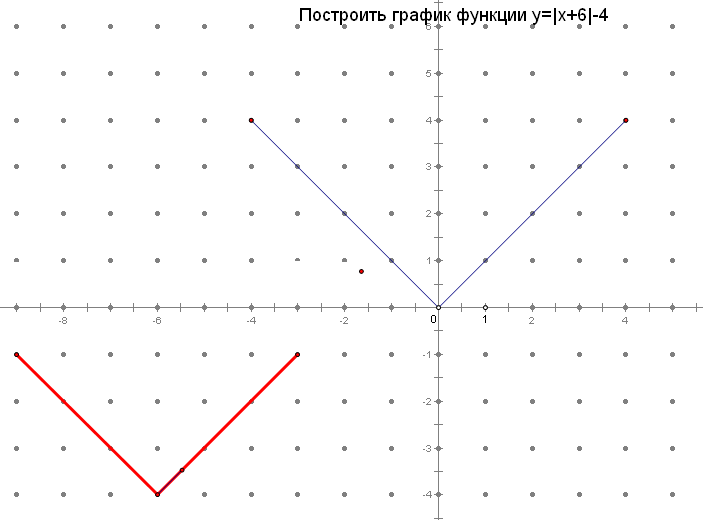
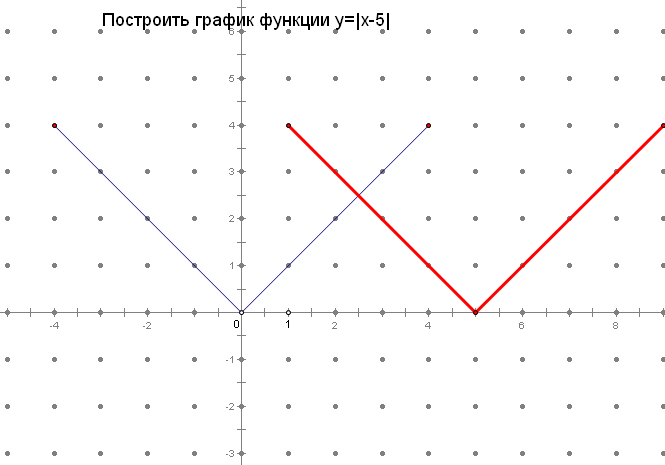
Сейчас мы рассмотрим с вами, построения графиков, более сложных.
Рассмотрим функцию вида y=||x+2|-3|
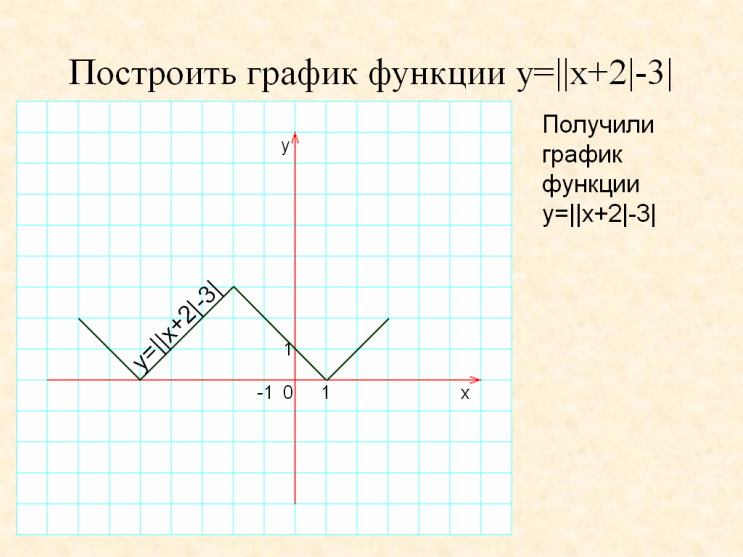
Рассмотрим функцию вида y=|||x|-3|-2| (слайд 17)
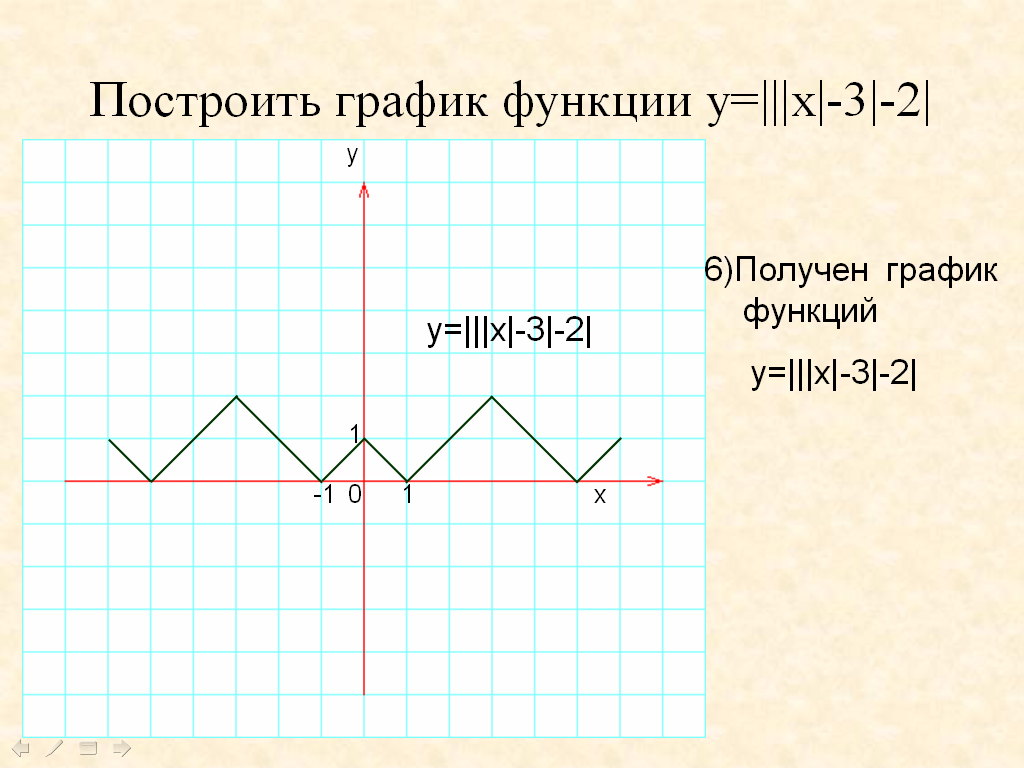
Учитель: Ребята, кто из вас сейчас попробует, в программе «Живая геометрия» построит график функции вида у=|||x-a|+b|+c|.
Ну а сейчас я вам покажу, как строить графии функции, содержащих сумму нескольких модулей. Рассмотрим случай, когда уравнение функции содержит сумму двух модулей. (слайд 18-19)

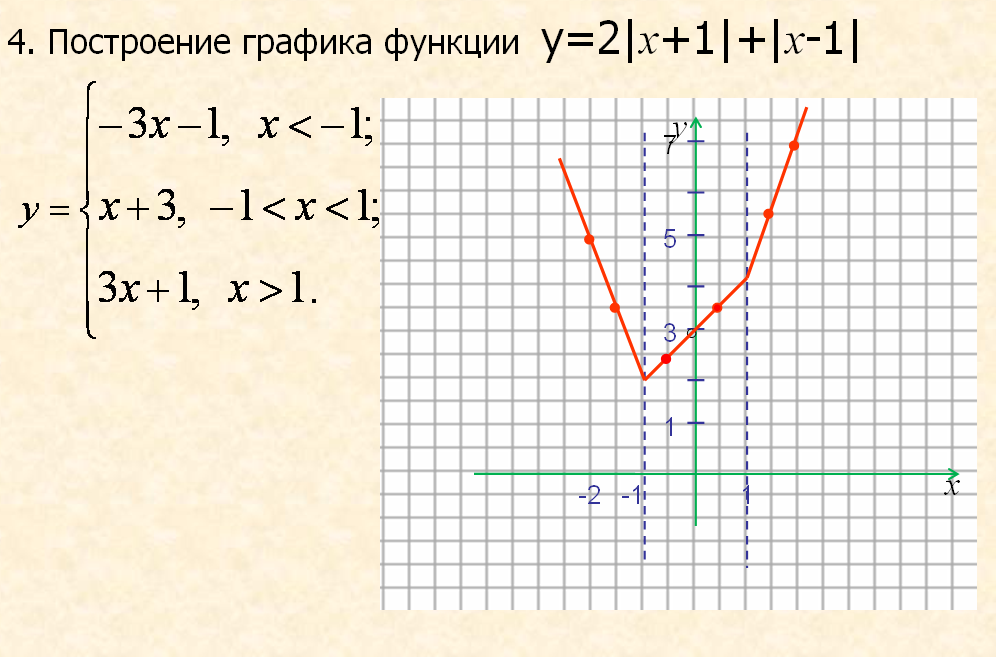
Учитель: А вы знаете, ребята, что полученные навыки построения графика функции вида у=|||x-a|+b|+c| применяется при решении уравнений и неравенств, систем уравнений и неравенств, графическим способом.
(слайд 20-23)
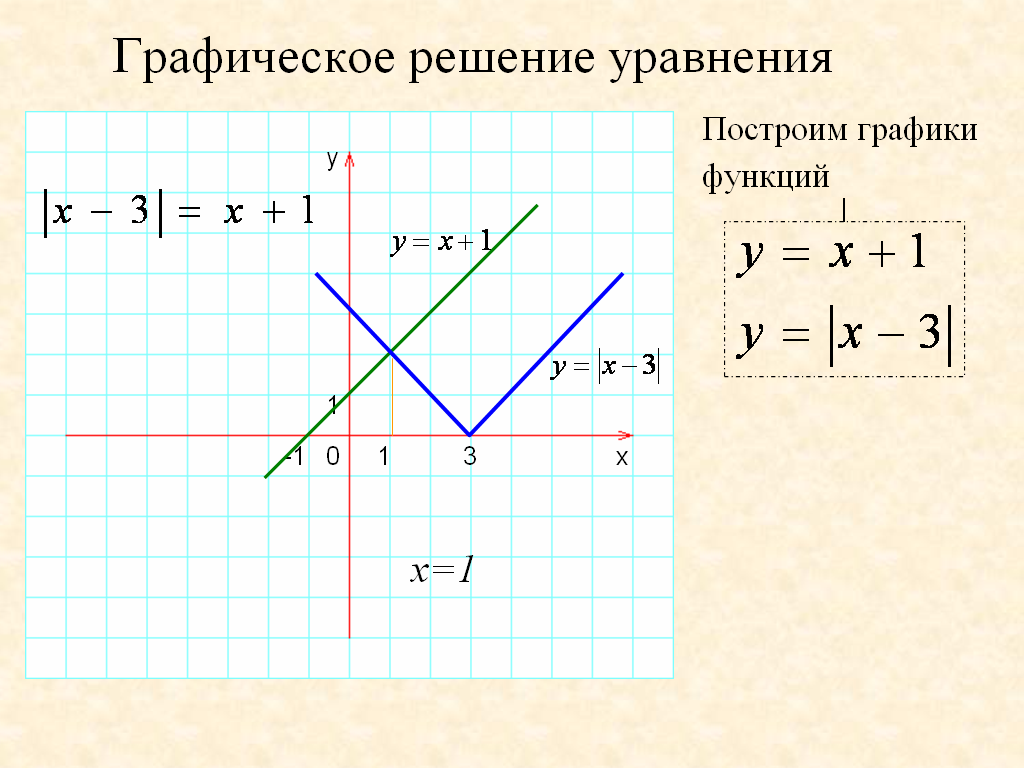

И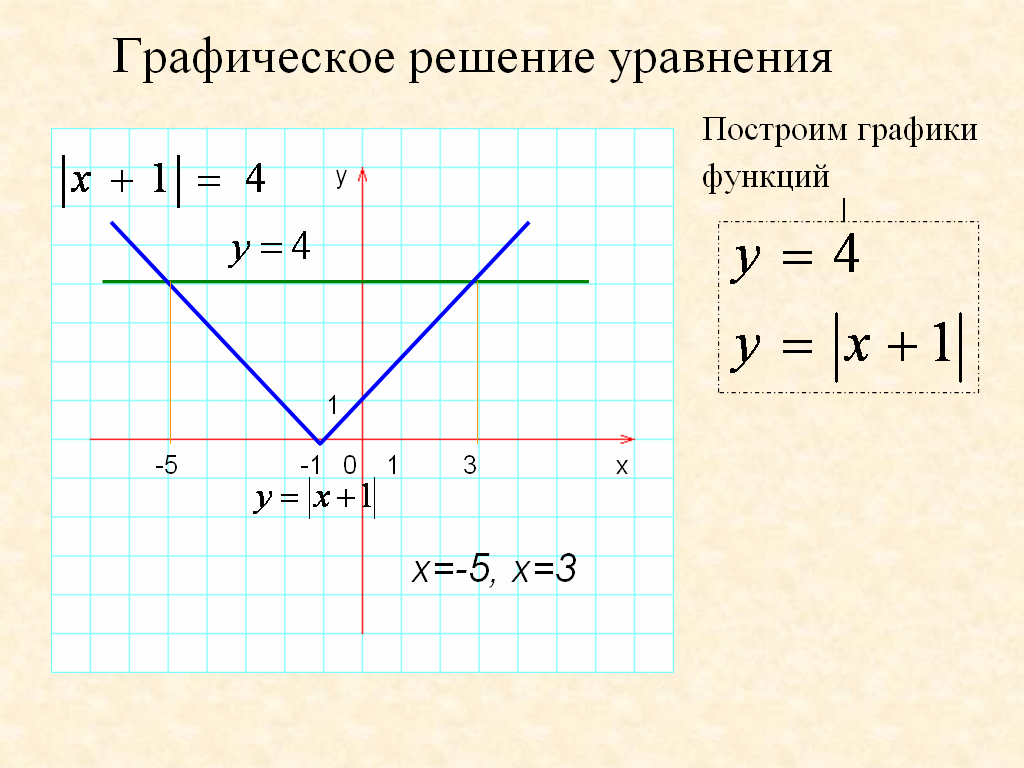
 тог урока. Сегодня на уроке мы рассмотрели функцию у=|x|, её свойства, график, рассмотрели метод построения графиков вида у=|||x-a|+b|+c|, применение полученных навыков на практике.
тог урока. Сегодня на уроке мы рассмотрели функцию у=|x|, её свойства, график, рассмотрели метод построения графиков вида у=|||x-a|+b|+c|, применение полученных навыков на практике.
Домашнее задание:
8







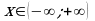 .
. y=kx.
y=kx.
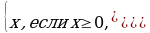
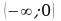 и полуинтервал
и полуинтервал  , т.е. при
, т.е. при 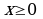 это биссектриса 1 координатной четверти, а при
это биссектриса 1 координатной четверти, а при 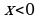 - второй. Итак, график функции у=|x| выглядит следующим образом.
- второй. Итак, график функции у=|x| выглядит следующим образом. 







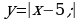 б)
б)  а)
а) 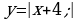 б)
б) 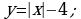
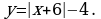 в)
в) 










 тог урока. Сегодня на уроке мы рассмотрели функцию у=|x|, её свойства, график, рассмотрели метод построения графиков вида у=|||x-a|+b|+c|, применение полученных навыков на практике.
тог урока. Сегодня на уроке мы рассмотрели функцию у=|x|, её свойства, график, рассмотрели метод построения графиков вида у=|||x-a|+b|+c|, применение полученных навыков на практике. 









