Технологическая карта занятия № __________
Преподаватель: ______________________
Дисциплина: Математика (тригонометрия)
Группа _________________
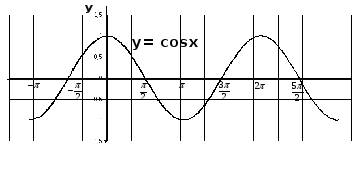
Тема: Функция у = cos x, ее свойства и график
Цели урока:
Изучить свойства функции у=cosх, выработать у учащихся умение изображать график схематически и по графику определять свойства функции
Подготовить к применению полученных знаний при решении уравнений графическим способом вычислении значения функции и выполнении преобразований графика функции у=cosх.
Развивать логическое мышление, внимание, навыки самостоятельной работы, навыки самооценки.
Вырабатывать у учащихся графическую культуру, внимательность, аккуратность и привить исследовательские навыки.
Задачи урока:
Изучить свойства функции у=cosх, выработать умение изображать график схематически.
Научить находить по графику область определения и область значений функции, промежутки возрастания и убывания функции, промежутки знакопостоянства, нули функции, наибольшее и наименьшее значение функции.
Тип занятия: Урок изучения нового материала.
Вид занятия: Урок – беседа с элементами исследования
Форма работы: Групповая, индивидуальная.
Обеспечение занятия средствами обучения: Компьютер, экран, презентация в формате PowerPoint, карточки с практическими заданиями, рисунки, графики чертежные инструменты
Ход урока
Организационный момент: Настрой на урок. Проверка готовности группы к уроку и приветствие всех присутствующих.
Сообщение темы и целей урока: Ознакомление с порядком проведения урока, рекомендации обучающимся, на что необходимо обратить особое внимание, что следует записать в рабочую тетрадь.
Сообщение темы, с помощью наводящих вопросов подведение обучающихся к формулировке цели занятия.
Как вы думаете: чем мы сегодня будем заниматься?
Что значит изучить свойства?
Какова схема исследования функции?
Общая схема исследования функции (повторение)
Область определения функции;
Множество значений функции;
Определение точек пересечения графика функции с осями координат;
Исследование функции на четность;
Исследование функции на периодичность.
Исследование функции на монотонность;
Определение промежутков знакопостоянства.
Построение графика функции.
(краткое пояснение всех пунктов)
3.Изучение нового материала:
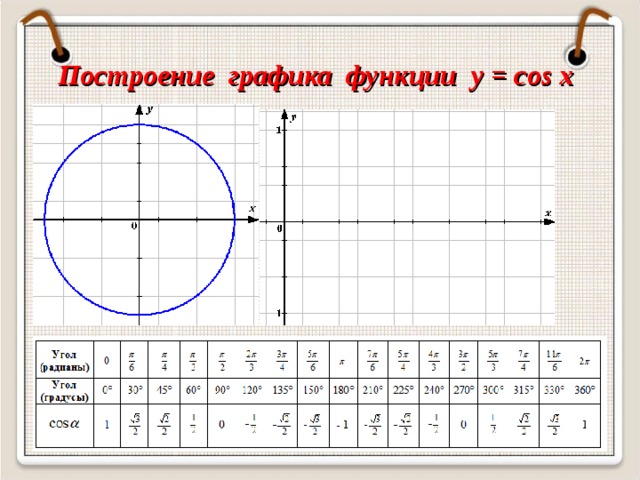
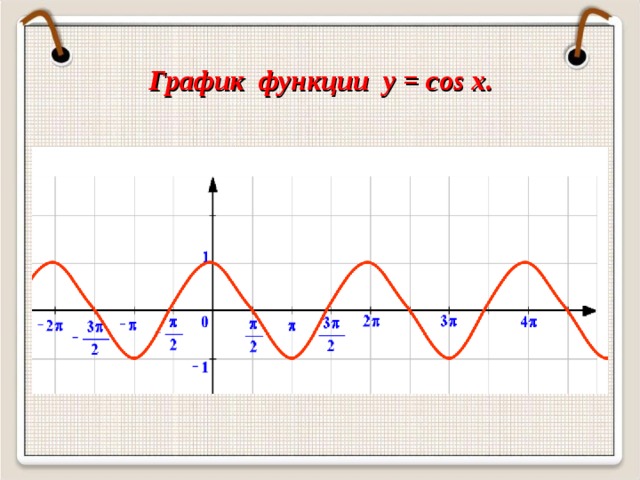
Функция y = cos x (приложение 1, 2)
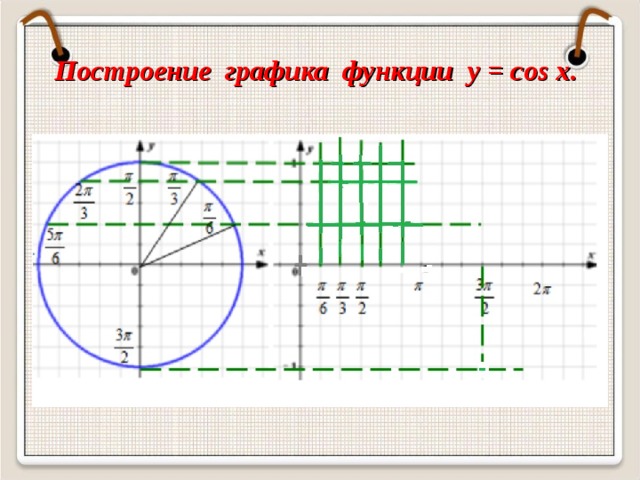
Построение графика. По точкам.
Исследование свойств, заполнение таблицы.
Область определения - это те значения переменной, при которых функция существует.
Множество значений функции – это все значения, которые принимает функция на своей области определения
У = 0 или Х = 0
Четная f(-х) = f(х); нечетная f(-х) = - f(х)
Периодической функцией называется функция, повторяющая свои значения через какой-то ненулевой период. Периодом функции называется число, при добавление которого к аргументу функции значение функции не меняется.
Промежутки возрастания и убывания функции
У 0;
Построение функции y = cos x в программах Excel u Equation Grapher
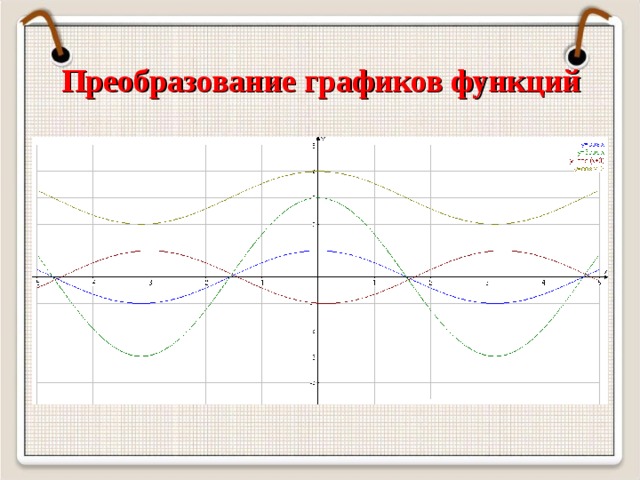
Преобразование графика функции y = cos x
Первичное закрепление, повторение опорных знаний тесты. (приложение 3)
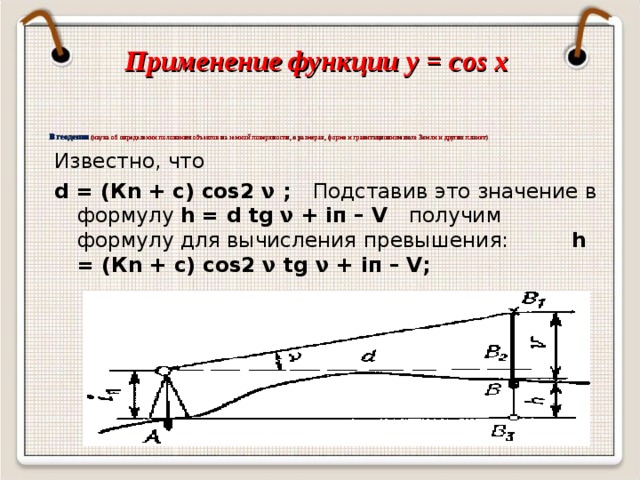
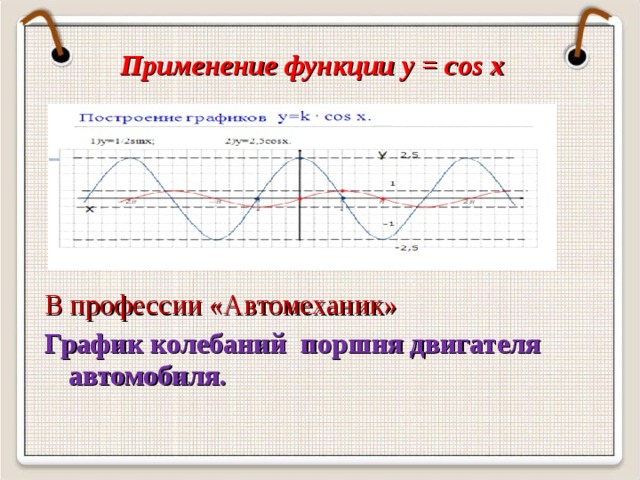
Применение функции y = cos x
А где в жизни пригодится функция косинуса или синуса?
Наиболее эффективно синусы и косинусы применяются учеными и инженерами. Синусы и косинусы часто присутствуют в формулах разных расчетов, инженерных или научных. Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности. Применение тригонометрических функций можно найти в различных отраслях науки, техники, просто в жизни.
Автомеханики (При изучении балансировки колес, резонансных систем автомобиля и т.д.)
Электрики (При изучении электромагнитных волн – гармонические колебания)
Сварщики (При подготовке металла к сварке и резке)
Построить график функции, выявить ее свойства:
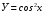
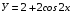
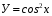
Домашнее задание: продумать где функция y = cos x находит применение в профессии сварщик
Рефлексия
С какими трудностями вы встретились сегодня на уроке?
Как с ними справились?
Что удивило на уроке?
С каким настроением покидаете урок?
Приложение 1
Построение графика функции (по точкам)
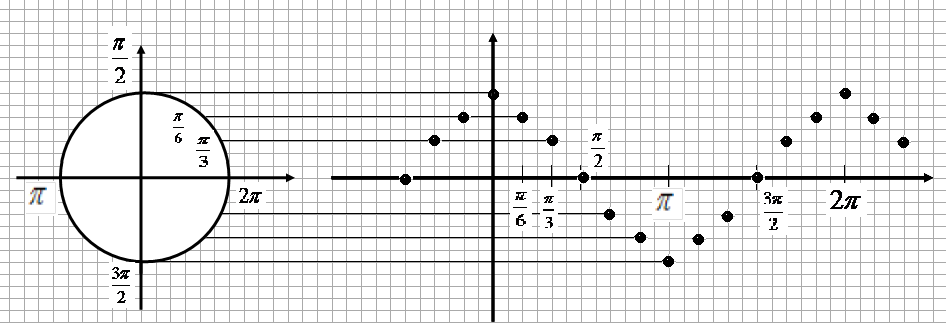
Приложение 2
Таблица по теме «Функция у = cos x»
 Свойства Функции у = cos x»
Свойства Функции у = cos x»
Х
|
| Свойства Функции | у = cos x» |
| 1 | Область определения D(y) |
|
| 2 | Множество значений E(y) |
|
| 3 | У = 0 |
|
|
| Х= 0 |
|
| 4 | Четность (нечетность) |
|
| 5 | Период |
|
| 6 | Возрастает |
|
|
| Убывает |
|
| 7 | У |
|
|
| У 0 |
|
Приложение 2а
Таблица по теме «Функция у = cos x»
 Свойства Функции у = cos x»
Свойства Функции у = cos x»
Х
|
| Свойства Функции | у = cos x» |
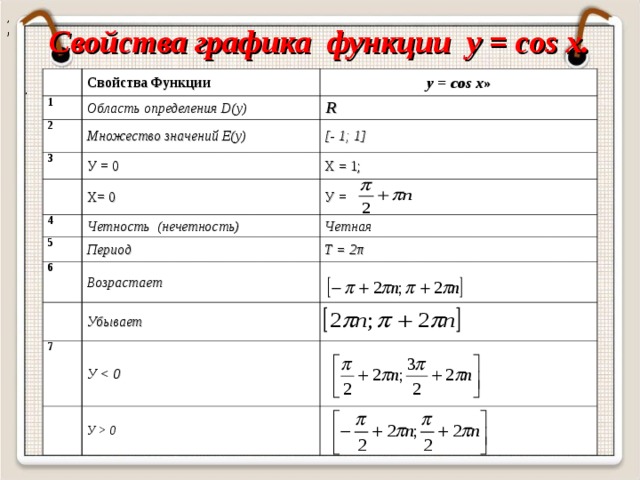
| 1 | Область определения D(y) | R |
| 2 | Множество значений E(y) | [- 1; 1] |
| 3 | Х = 0 | У = 1; |
|
| У = 0 | Х = 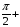 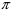 n n |
| 4 | Четность (нечетность) | Четная |
| 5 | Период | Т = 2π |
| 6 | Возрастает | 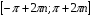 , ,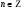 , ,
|
|
| Убывает | 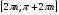 , , 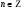 . .
|
| 7 | У | 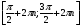 . .
|
|
| У 0 | 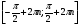
|
Приложение 3
ТЕСТИРОВАНИЕ
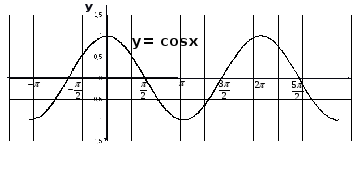
График какой функции изображен на рисунке
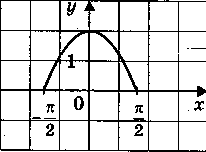
Y = cos 0.5 x
Y = 2cos x
Y = 2cos 0.5x
Y = 2 sin x
Исправьте ошибку 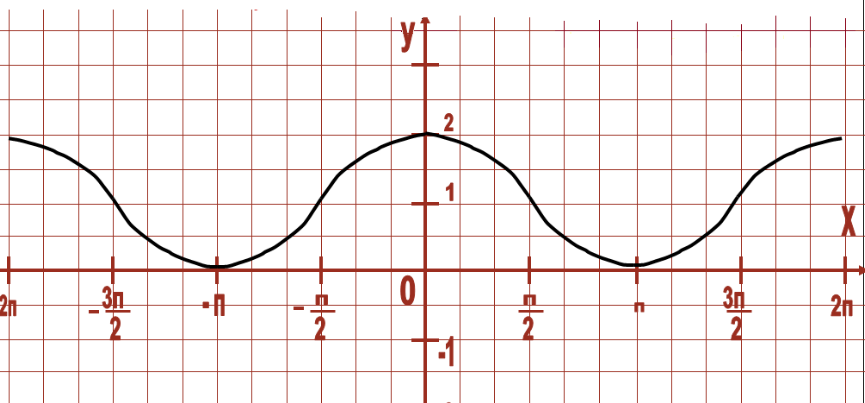
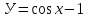
Укажите множество значений функции

[-4; 4]
[-5; -3]
[1; 4]
[-4 ; -3]
Укажите функцию, множеством значений которой является промежуток [-1; 1]

На вопросы нужно отвечать только «Да» или «Нет»:
sin2 + cos2 = 1 – основное тригонометрическое тождество;
sin x, cos x, tg x, ctg x – тригонометрические функции;
[0; 1] – область значения функции cos x;
Функция у = cos x четная;
Период функции у = cos x равен π
Тригонометрия – раздел геометрии.
Приложение 3а
Ключи к тестам
2
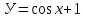
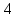
2
Да – 1, 2, 4, 6.
Нет – 3, 5.







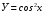
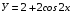
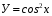

 Свойства Функции у =
Свойства Функции у =  Свойства Функции у =
Свойства Функции у = 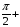
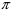
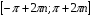 ,
,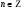 ,
,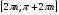 ,
, 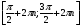 .
.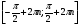


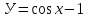


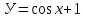
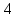




 0 ." width="640"
0 ." width="640"