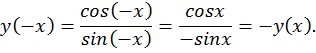Дата: 03.04.2020.
Тема: ФУНКЦИЯ y = ctg x
Цели: рассмотреть свойства функции котангенс и построить её график; закрепить новые знания в ходе решения задач.
Ход урока
-
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Вспомните самостоятельно теорию, которая была изучена нами на прошлых уроках для функций y=sin x, у=соs x и y = tg x. Ответьте устно на вопросы.
-
Что называется областью определения функции? Каковы они для изученных функций?
-
Что называется множеством значений функции? Каковы они для изученных функций?
-
Как называются графики изученных ранее функций?
-
Что называется котангенсом угла α?
-
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Откройте свои тетради и запишите сегодняшнее число и тему урока. Далее выполняем построение графика функции у=ctg x и переписываем её свойства.
Давайте подумаем, как построить график функции у=ctg x? Вспомним формулу взаимосвязи

Т.е. график функции у=ctg x можно получить из графика функции y = tg x с помощью применения элементарных преобразований. Вспомним график функции y = tg x. К нему необходимо применить такие преобразования: смещение графика по оси Ох и отображение его симметрично относительно оси ОХ.
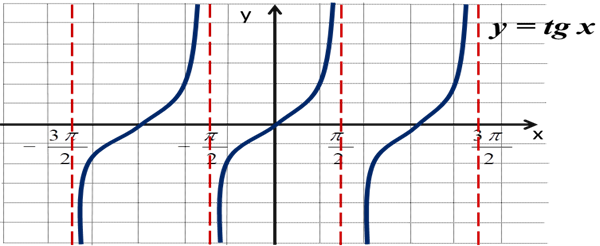
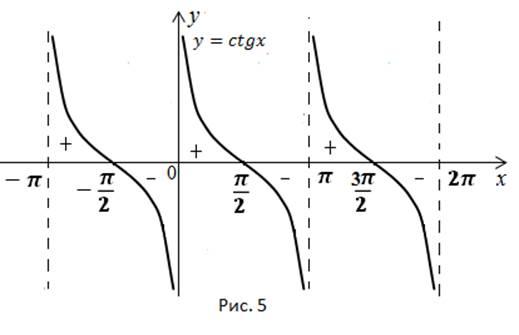
Применив эти преобразования, получим график для функции у=ctg x
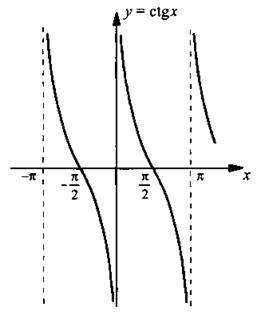
Перечислим основные свойства функции у = ctg x:
1. Область определения - множество всех действительных чисел, за исключением чисел вида х = πk, к ∈ Z.
2. Функция нечетная (т. е. у(-х) = -y(x)), и ее график симметричен относительно начала координат.
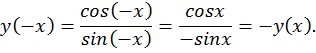
3. Функция убывает на промежутках вида (πk; π + πk), к ∈ Z.
4. Функция не ограничена.
5. Функция не имеет наименьшего и наибольшего значений.
6. Функция непрерывная.
7. Область значений Е(у) = (-∞; +∞).
8. Функция периодическая с наименьшим положительным периодом Т = π, т. е. у(х + πk) = у(x).
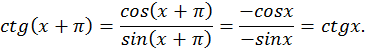
9. График функции имеет вертикальные асимптоты х = πk.
10. Точки пересечения с осью Оx:
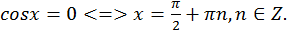
Точки пересечения с осью Оy отсутствуют.
11. Определим интервалы знакопостоянства:
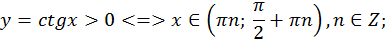
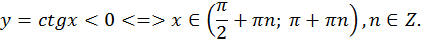
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Пользуясь свойствами функции y = сtg x, выполните письменно №10.28, №10.31.
-
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Какие свойства функции y = сtg x запомнили?
Домашнее задание: теория, №10.32.