Г10 Площадь ортогональной проекции. п. 16 УМК Мерзляк Углубленный уровень

Площадь ортогональной проекции многоугольника.

Учитель математики Ильясова Н. А.

МБОУ «СОШ №14 с УИОП»

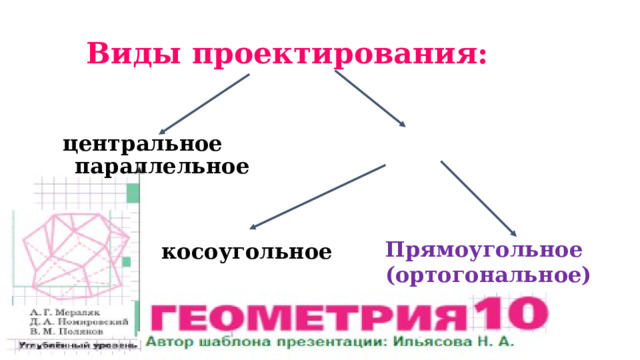
Виды проектирования:

центральное параллельное

Прямоугольное

(ортогональное)

косоугольное

Свойства ортогонального проектирования

• Проекцией прямой является прямая.
• Проекцией параллельных прямых

являются параллельные прямые.

• Сохраняется отношение отрезков, лежащих на параллельных прямых.

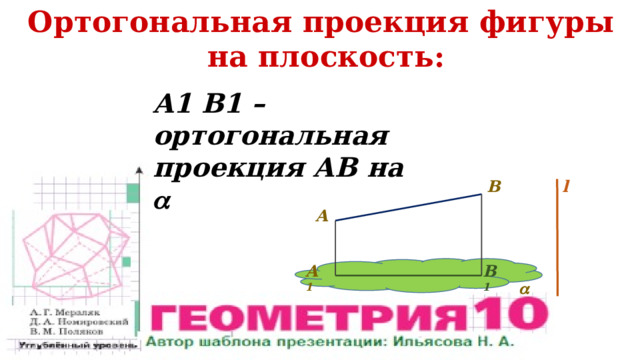
Ортогональная проекция фигуры

на плоскость:

A1 B1 –

ортогональная проекция АВ на 

B

l

A

B 1

A 1



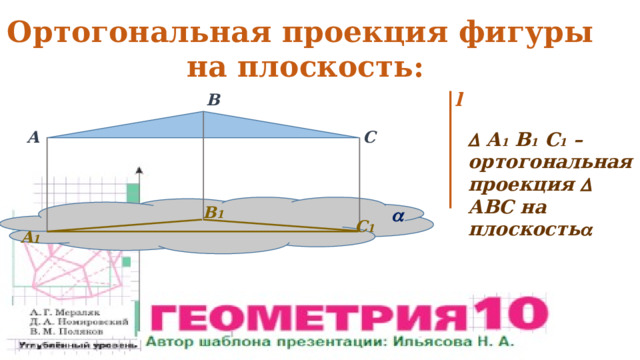
Ортогональная проекция фигуры

на плоскость:

l

B

C

A

 А 1 В 1 С 1 – ортогональная проекция  АВС на плоскость 

B 1



C 1

A 1

Ортогональная проекция фигуры

на плоскость:

 АВС и  А1 В1 С1 могут быть равны,

а могут быть и не равны.

РАВНЫ: если (АВС)   .

НЕ РАВНЫ: если угол между их

плоскостями 0    90  .

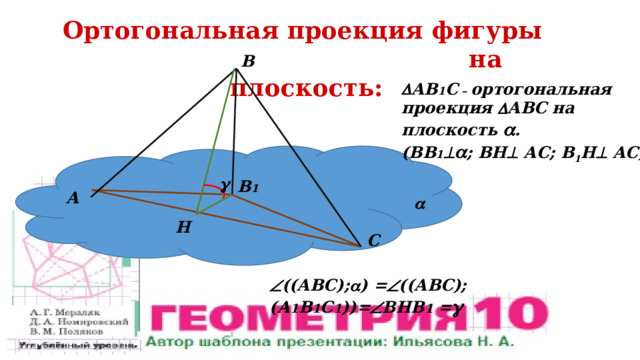
Ортогональная проекция фигуры

на плоскость:

В

 АВ 1 С – ортогональная

проекция  АВС на

плоскость  .

(ВВ 1   ; ВН  АС; В 1 Н  АС)



В 1

А



Н

С

 ((АВС);  ) =  ((АВС);(А 1 В 1 С 1 ))=  ВНВ 1 = 

S  AB1C =S  ABC  cos 

Площадь ортогональной проекции

треугольника равна произведению площади

треугольника на косинус угла между их

плоскостями.

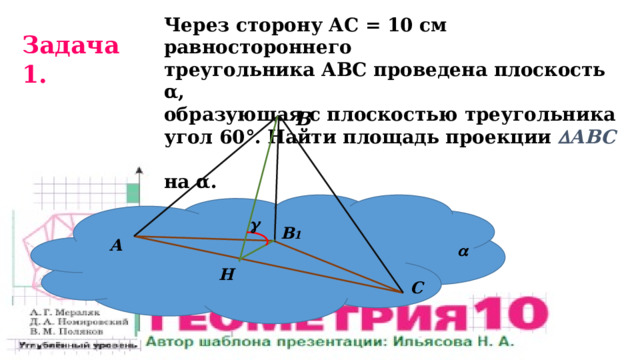
Через сторону АС = 10 см равностороннего

треугольника АВС проведена плоскость α,

образующая с плоскостью треугольника

угол 60°. Найти площадь проекции  АВС

на α.

Задача 1.

В



В 1

А



Н

С

Задача 2.

Ортогональной проекцией треугольника, площадь которого 420, является треугольник со сторонами 39; 17; 28 см. Найдите угол между плоскостями.