10
Гармонические колебания.
Метод аналогий при решении задач.
Общеизвестно, что «с точки зрения» математики все гармонические колебания одинаковы, так как описываются одними и теми же уравнениями. Например, выражение х = хm(cos wt + j0) в механике может описывать изменение со временем координаты, в электромагнетизме – заряда, силы тока или напряжения. Это позволяет решать некоторые сложные задачи путём их переформулирования, приводящего к другим, более легким.
После того, как вышел в свет учебник физики под редакцией А.А. Пинского для выпускного класса, где кратко описывается аналогия электромагнитных и механических колебаний, данная методика сразу была взята автором на вооружение и уже без малого десять лет используется на уроках. Результаты – превосходные. В этой работе приводятся примеры решения некоторых задач, использованных на уроках, контрольных работах и олимпиадах.
Для быстрого нахождения аналогий в колебаниях запишем закон сохранения энергии при незатухающих колебаниях груза на пружине и в колебательном контуре:

 m
m L
L
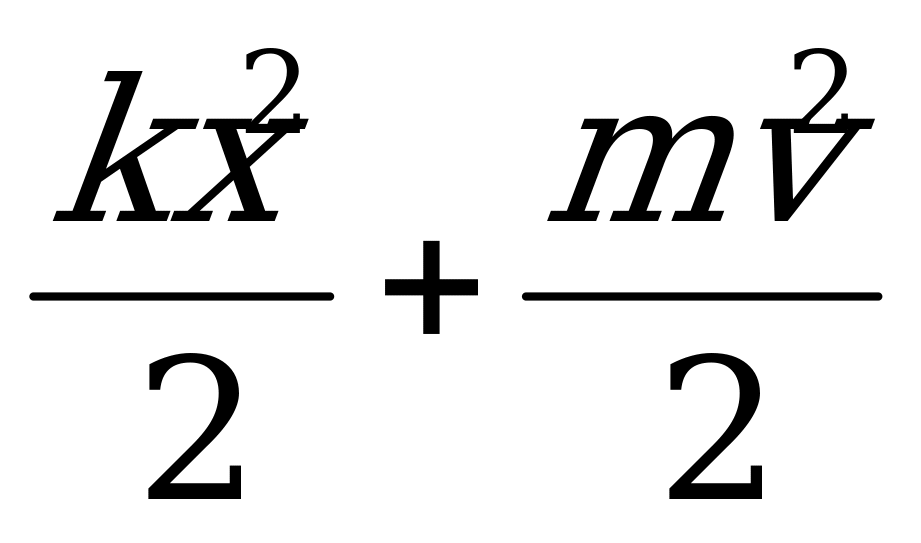 = const v
= const v I
I
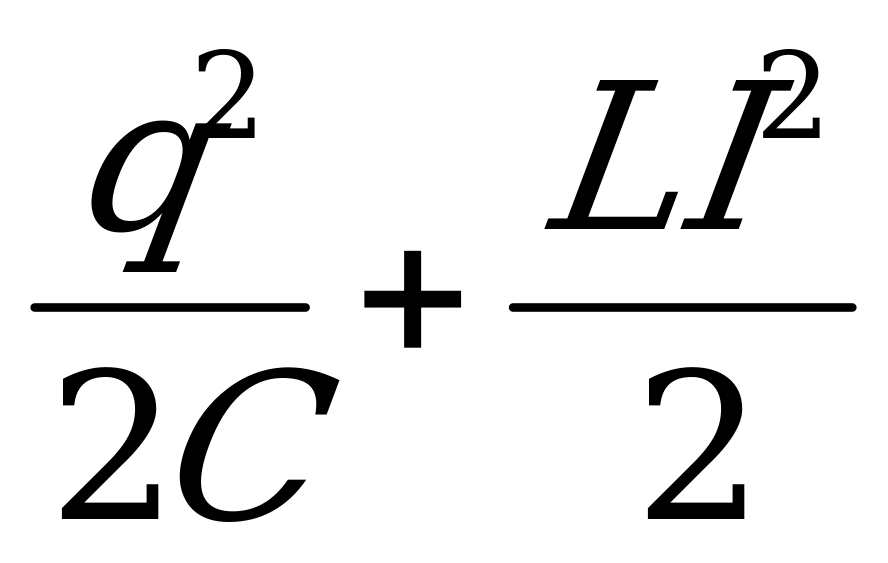 = const
= const  x
x q
q 
k
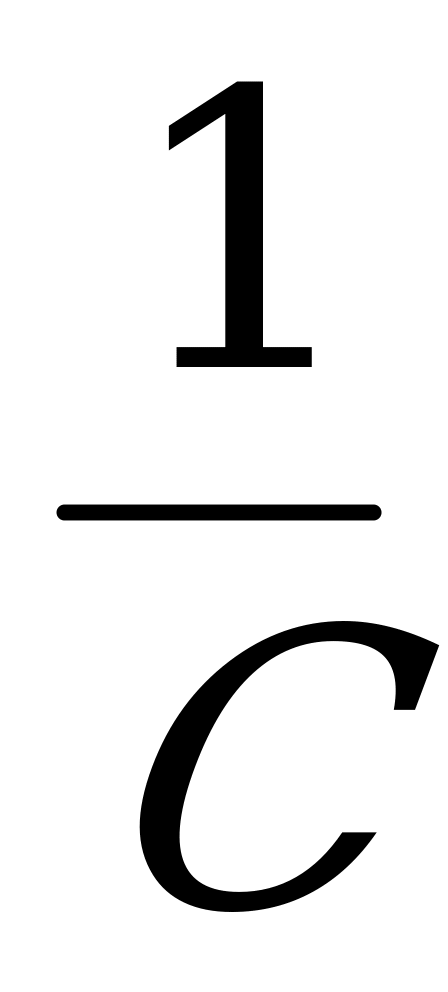
 x’’=v’=a
x’’=v’=a q’’=I’
q’’=I’
mv=P LI=F
LI=F
ma=F LI’=e=êj=F’
LI’=e=êj=F’
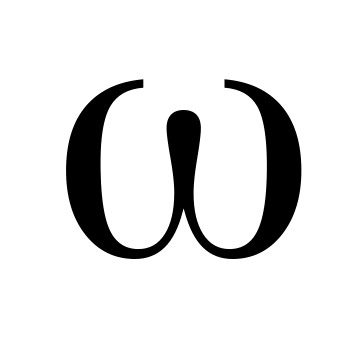 =
=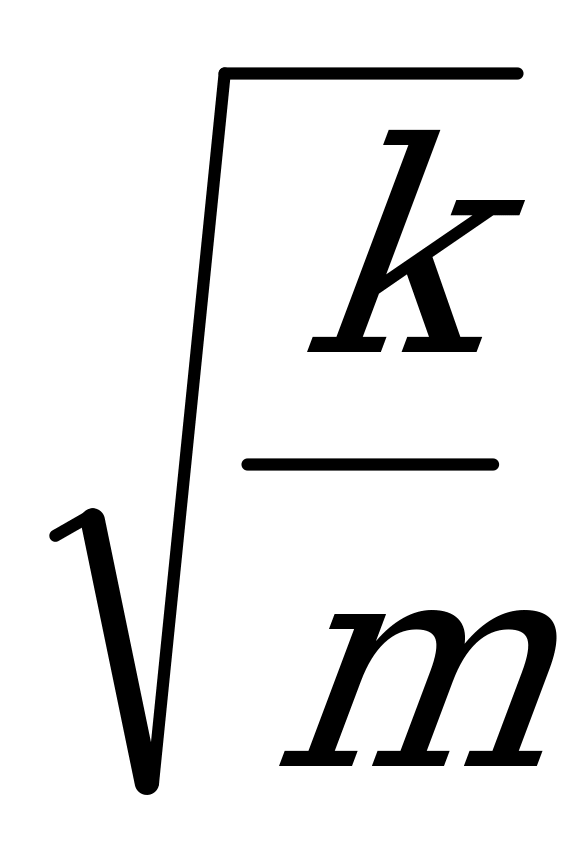


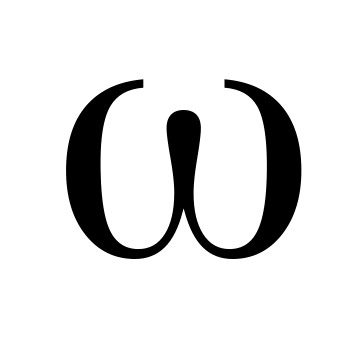 =
=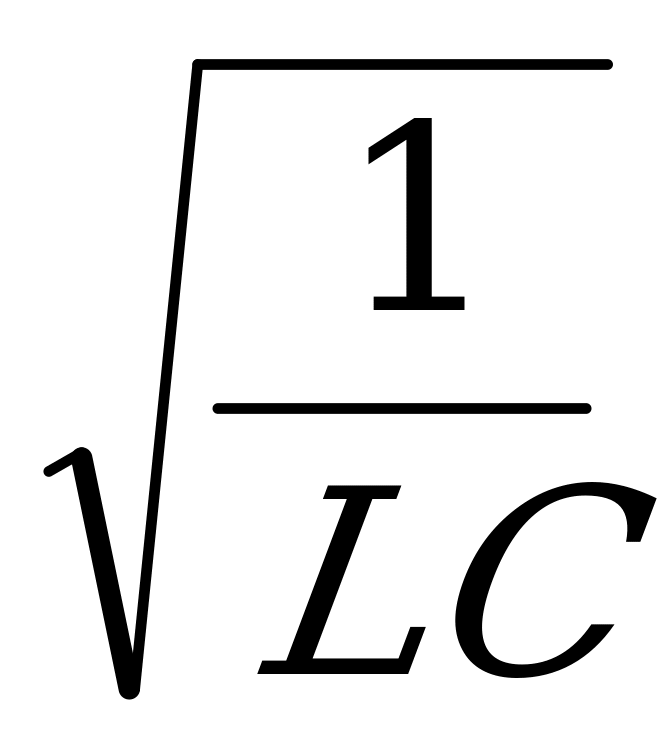
m1+m2+…+mn L1+L2+…+Lm
L1+L2+…+Lm
k1+k2+…+kn
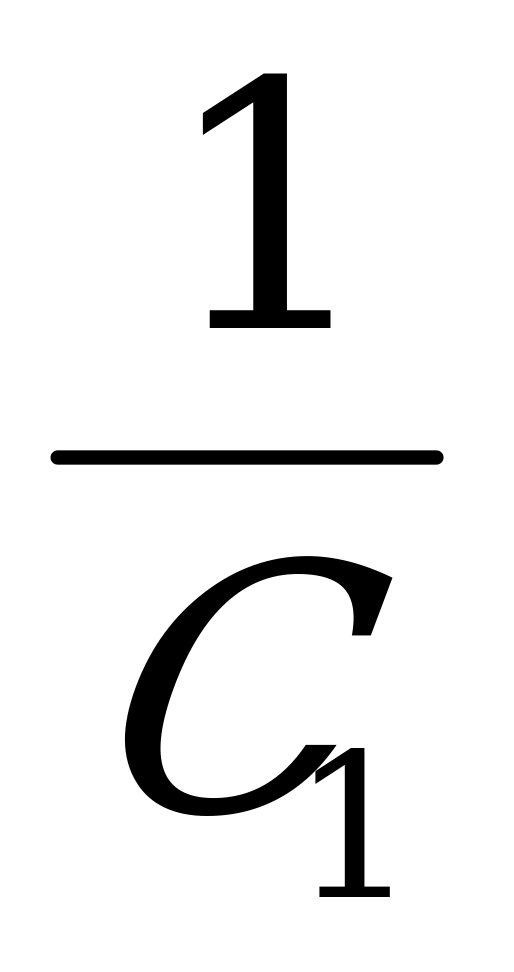 +
+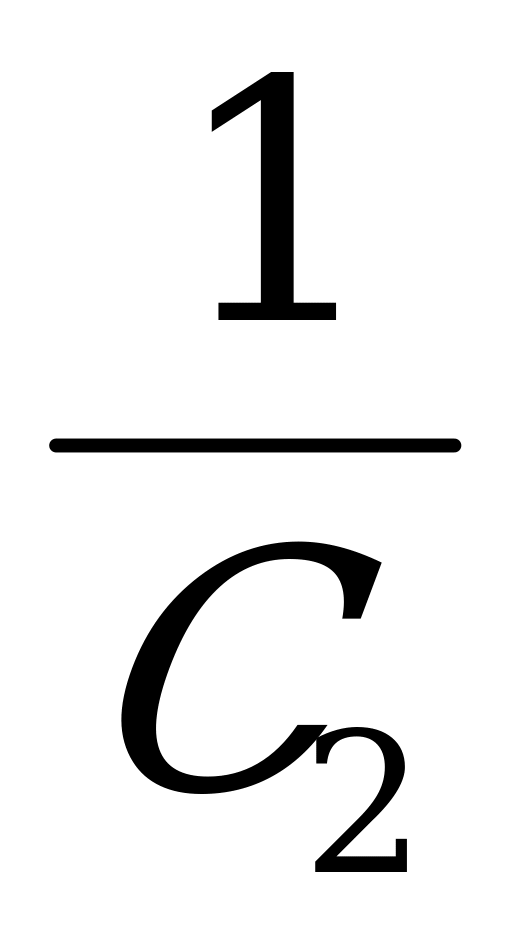 +…+
+…+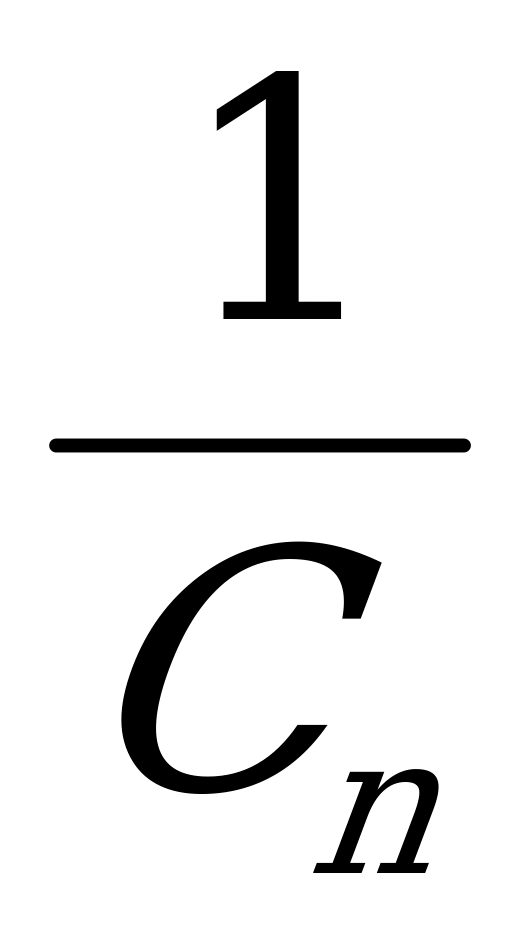
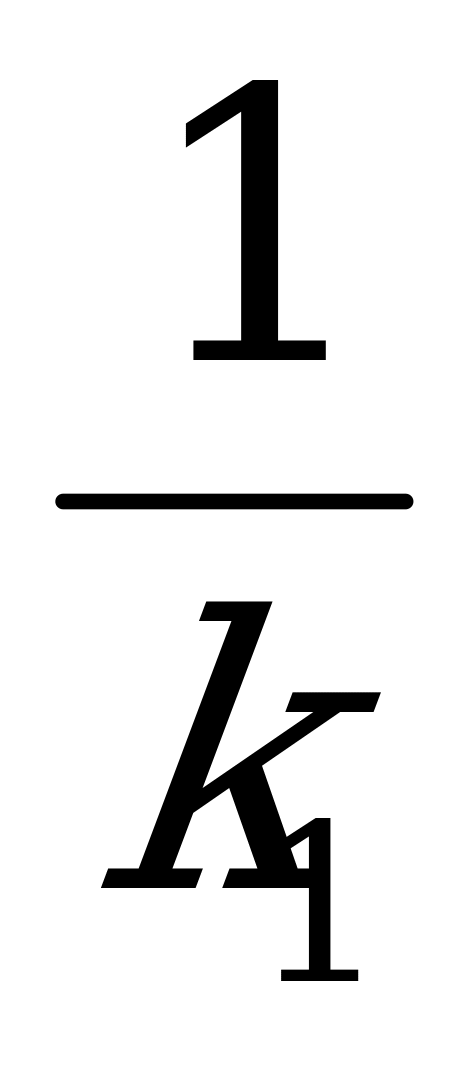 +
+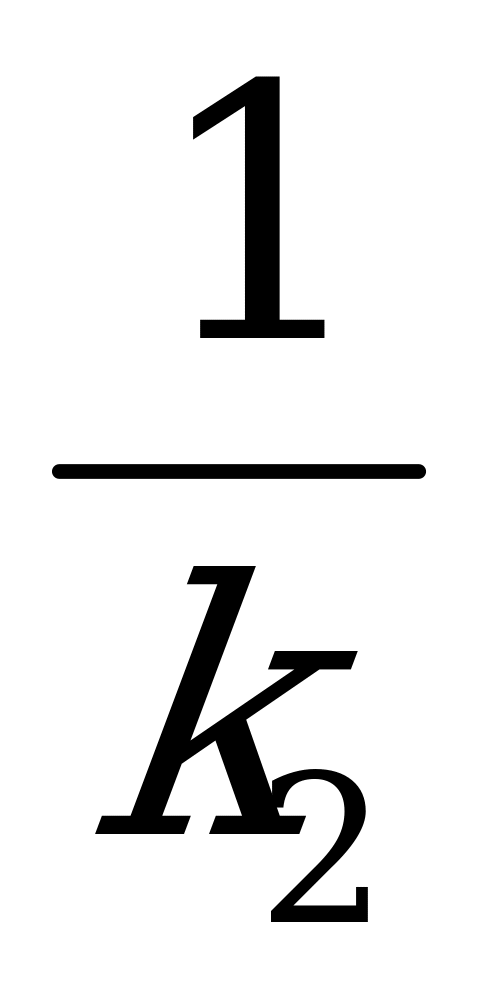 +…+
+…+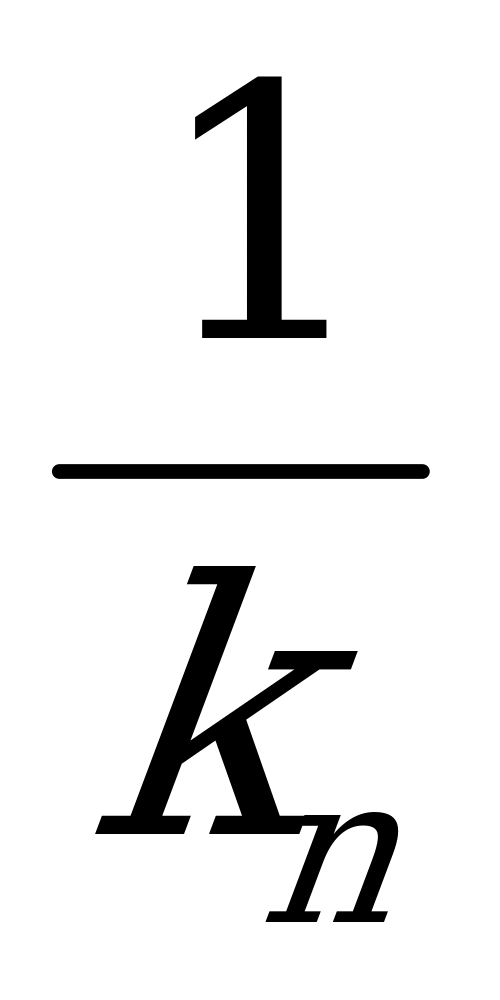
 С1+С2+…+Сn
С1+С2+…+Сn
и т.д.
Используя эти аналогии, можно получать и формулы. Например, 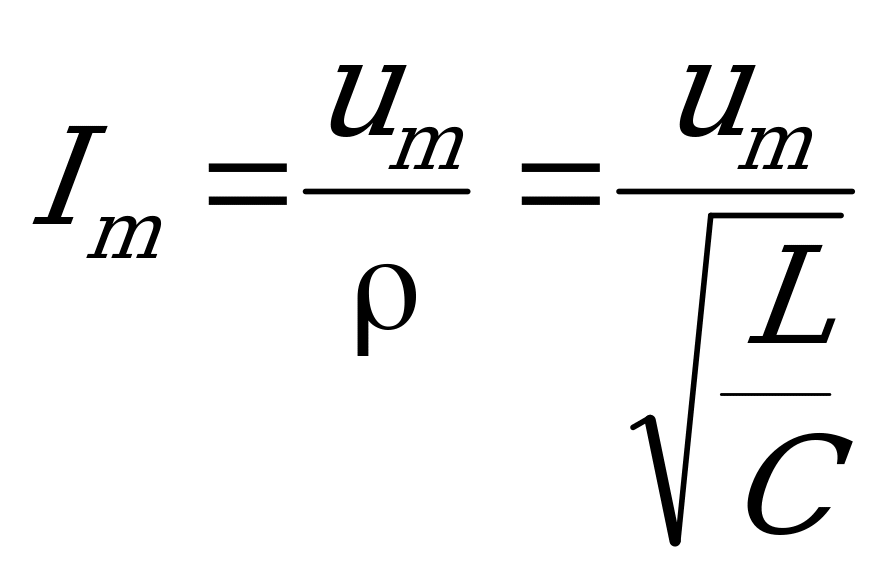 , где
, где 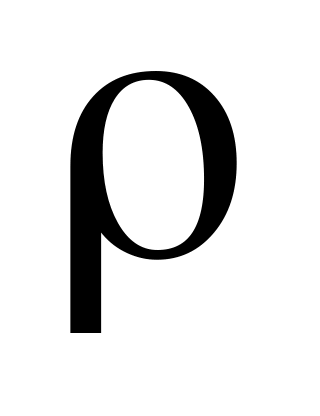 – волновое сопротивление контура. Соответственно в механике будем иметь:
– волновое сопротивление контура. Соответственно в механике будем иметь: 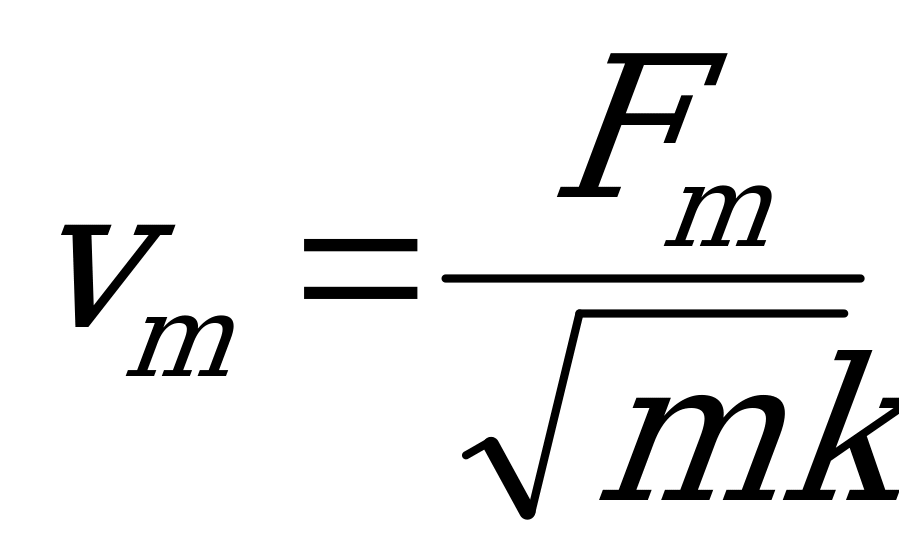 и т.д.
и т.д.
Можно также найти соответствие между следующими схемами:
k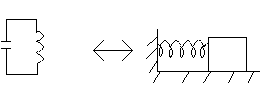 m
m
C L
m1 m2
k 1 k2
1 k2
c1 c2 L1 L2
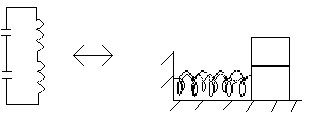
c1 L1
k1 k2 m2
c2 L2 m1
и т.д.
Перейдем к задачам.
Задача1.
Определите период незатухающих колебаний грузов массами m1и m2, соединенных пружиной, жесткостью k.Трение отсутствует.
m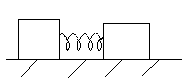 1 k m2
1 k m2
Решение 1.
Свяжем систему отсчета с центром масс тел, тогда он – неподвижен. Как следует из закона сохранения импульса, периоды колебаний обоих тел должны быть одинаковы, и задача сводится к нахождению периода колебаний одного из тел, например массой m1,прикрепленного более короткой пружиной к центру масс:
m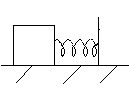 1
1
k1
Найдем жесткость k1. Вся пружина представляет собой две, жесткостью k1 и k2, соединенные последовательно, следовательно
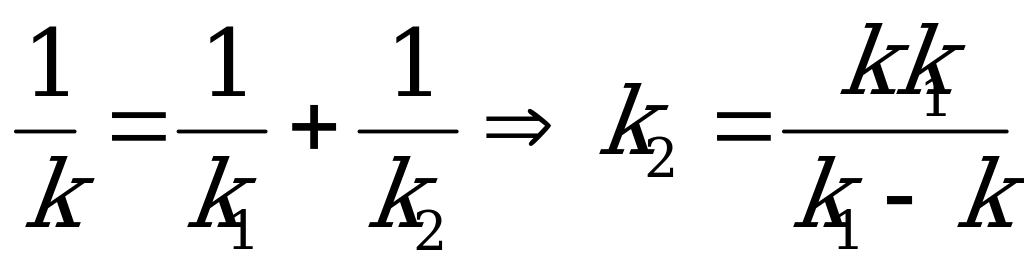


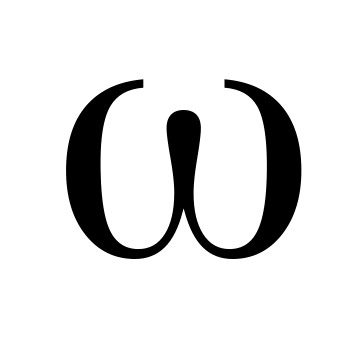 1=
1=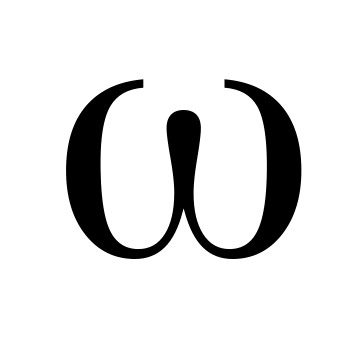 2=
2=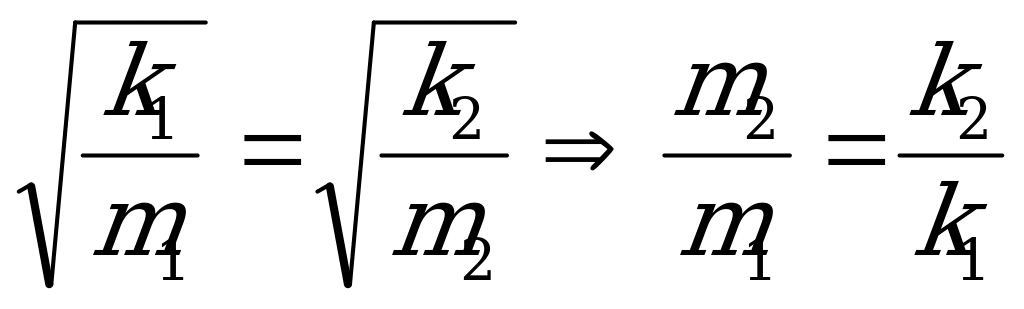


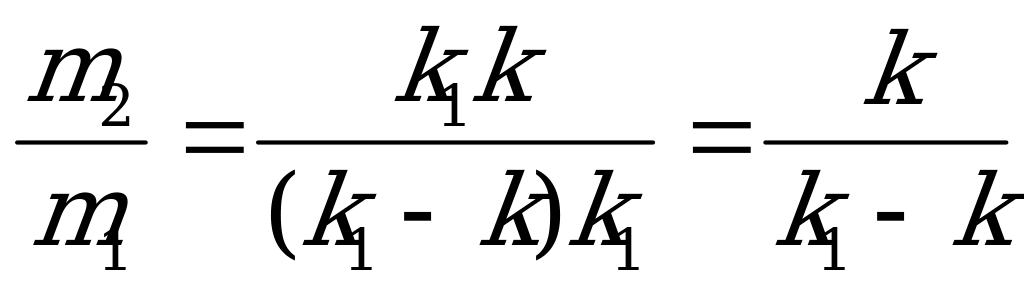

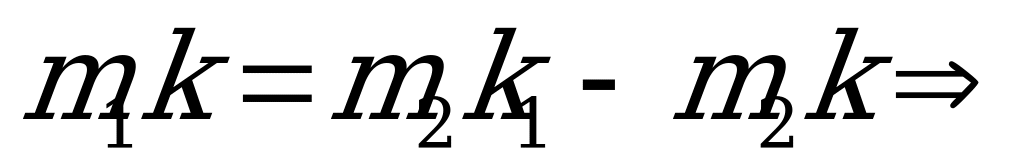
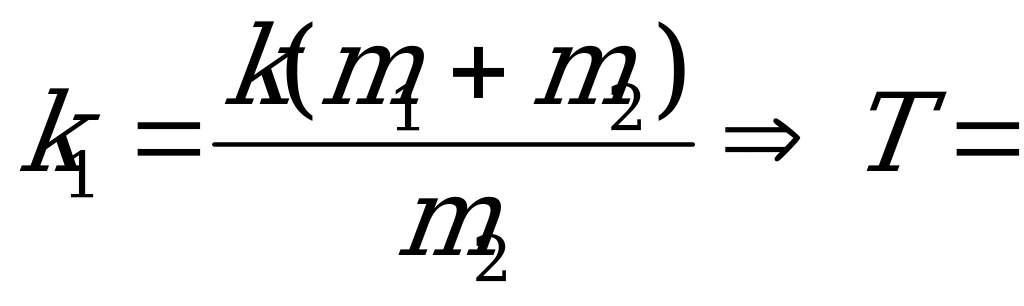
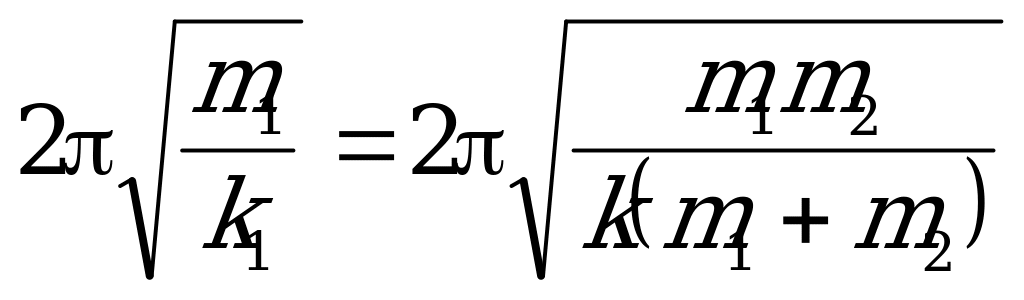
Решение 2.
Перейдем от механических к электромагнитным колебаниям:
C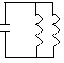 L1 L2
L1 L2
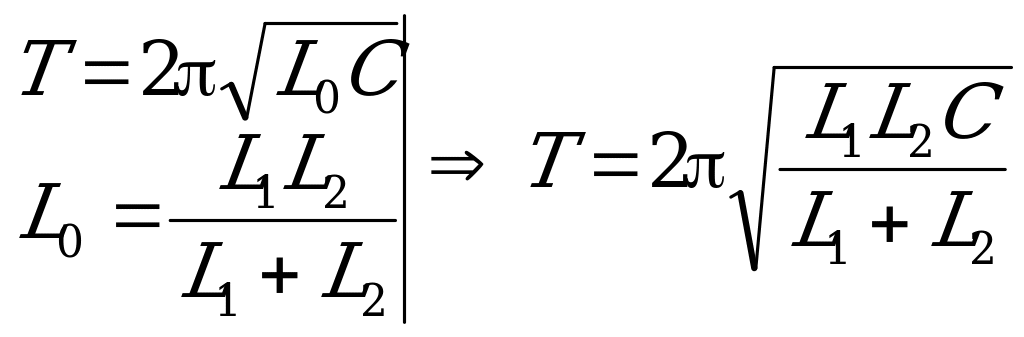 , что в задаче соответствует записи
, что в задаче соответствует записи 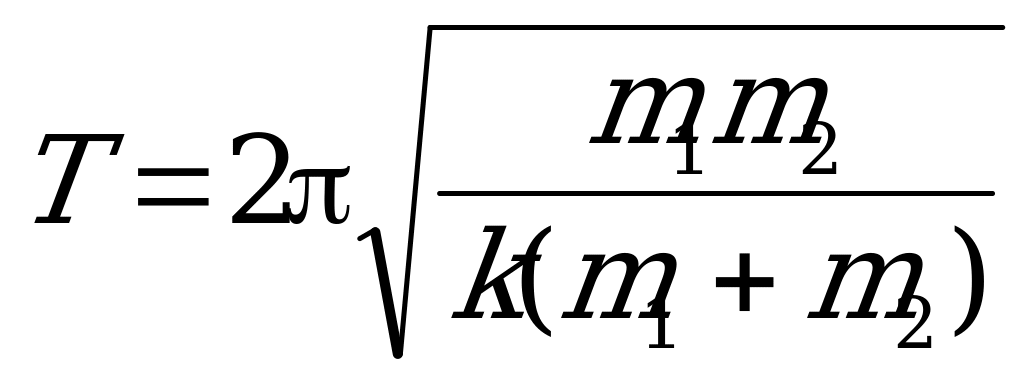
Задача 2.
В колебательном контуре совершаются незатухающие колебания. В момент, когда на конденсаторе с заряд достигает максимального значения qm, ключ к замыкают. Найдите новый период колебаний и максимальное напряжение на конденсаторе 2с.
2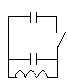 C
C
K
C
L
Решение 1.
После замыкания ключа конденсаторы практически мгновенно перезаряжаются. При этом закон сохранения энергии электростатического поля не выполняется, что можно доказать, использовав закон сохранения заряда: qm=qm1+qm2
Начальная энергия электрического поля:
W0=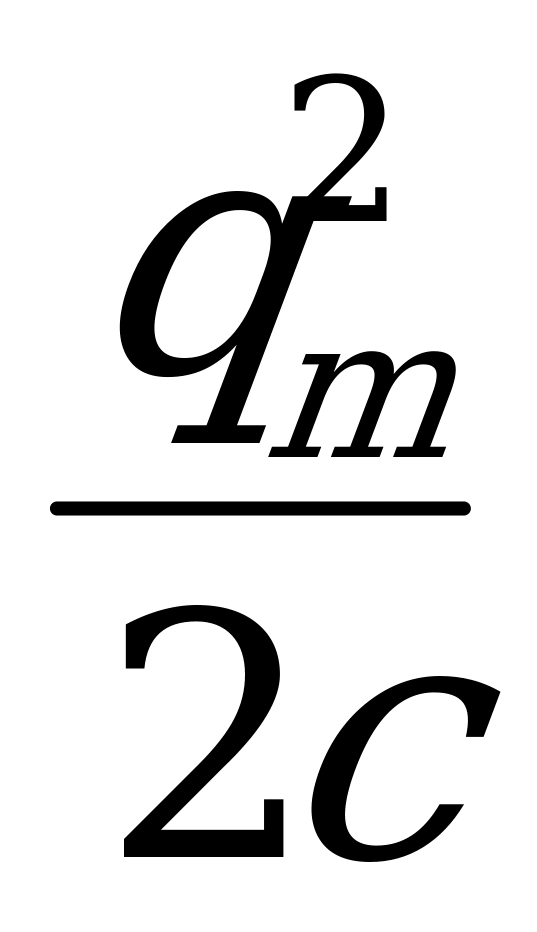 ; qm=qm1+qm2; qm1=cum1, qm2=2cum2
; qm=qm1+qm2; qm1=cum1, qm2=2cum2
Так как конденсаторы соединены параллельно, то
um1= um2; qm= cum1+2cum1 um1=
um1=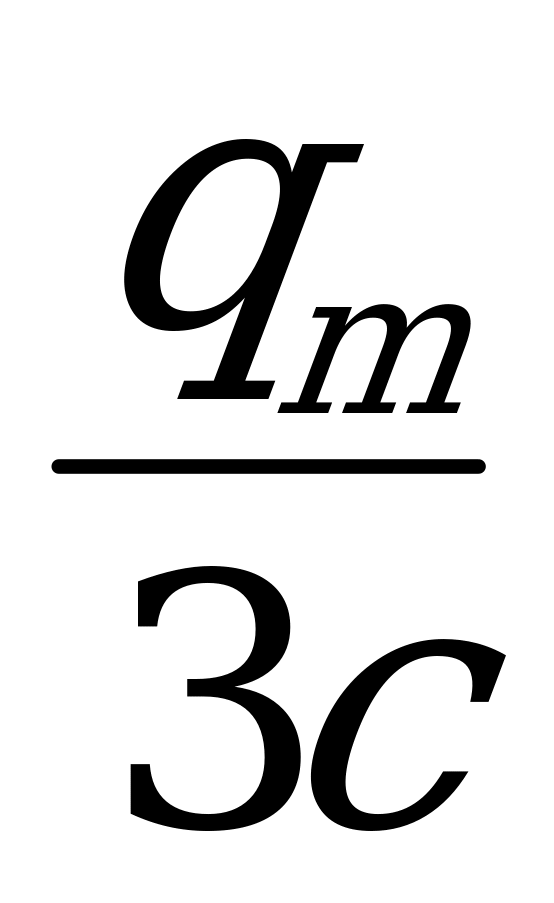
Энергия электрического поля сразу после замыкания ключа:
W1 + W2=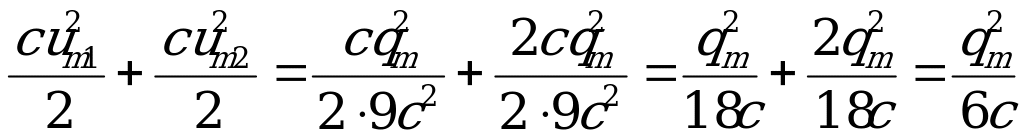
что в три раза меньше начальной энергии. Две трети ушло с электромагнитным излучением, так как электроны при перезарядке двигались с огромным ускорением.
Итак, максимальное напряжение на конденсаторе 2с равно: um2=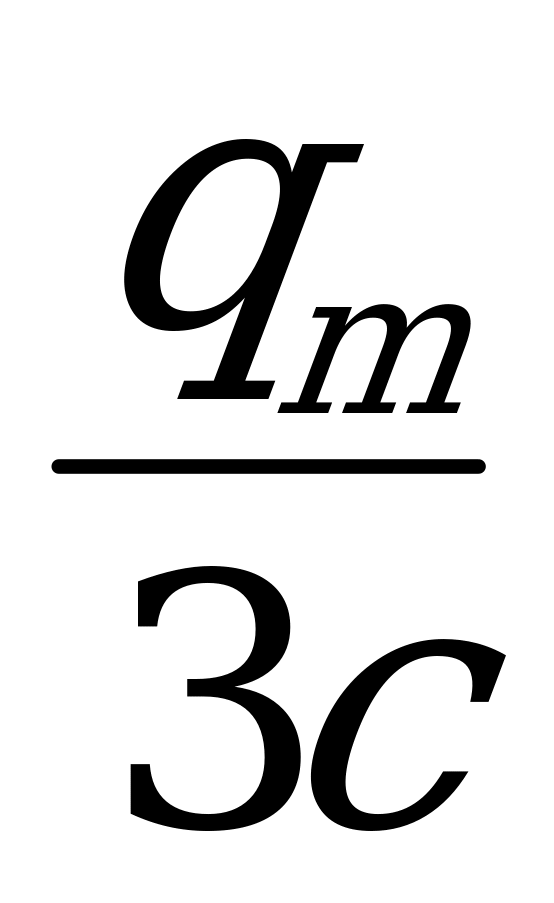
Новый период колебаний:
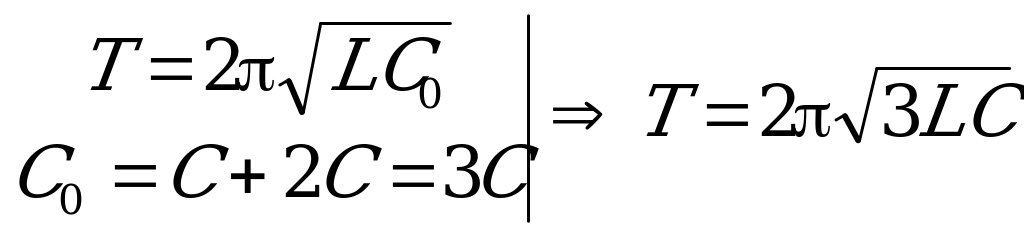
Сложности, возникающие ввиду того, что закон сохранения энергии электростатического поля не выполняется, что может привести к ошибке в решении, пропадают, если от электромагнитной системы перейти к механической.
Решение 2.
Перейдем от электромагнитных к механическим колебаниям:
А
k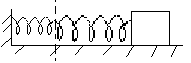 /2 k m
/2 k m
B
Пружина k максимально сжата (или растянута).После удаления перегородки АВ обе пружины практически мгновенно деформируются и только затем начинают действовать на груз m: 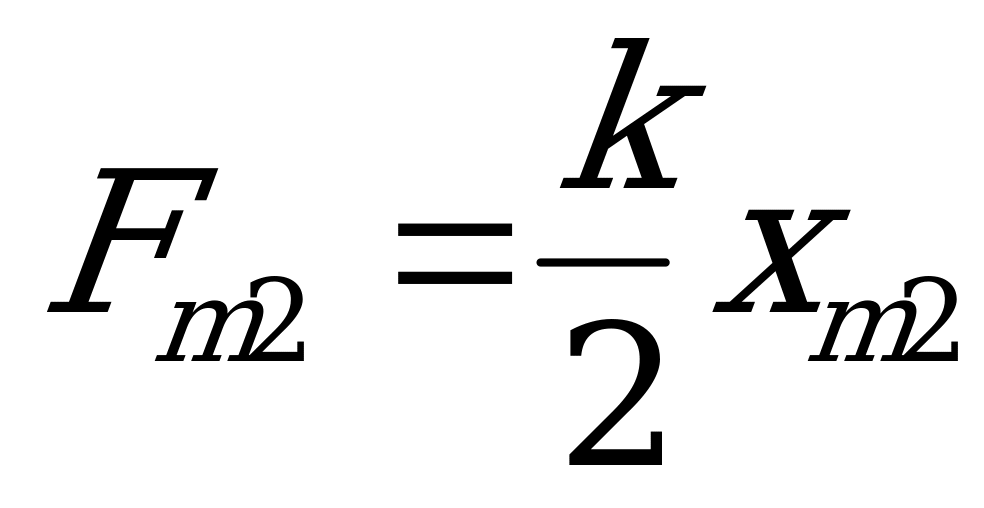 , но очевидно, что
, но очевидно, что 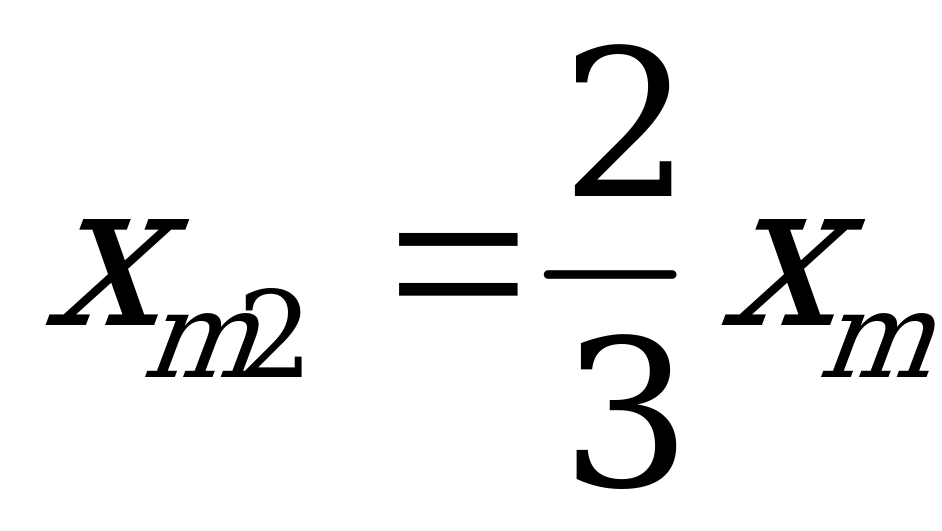 , так как
, так как 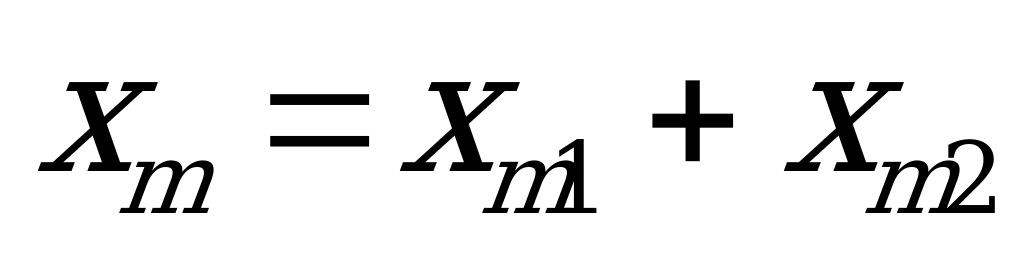 и
и 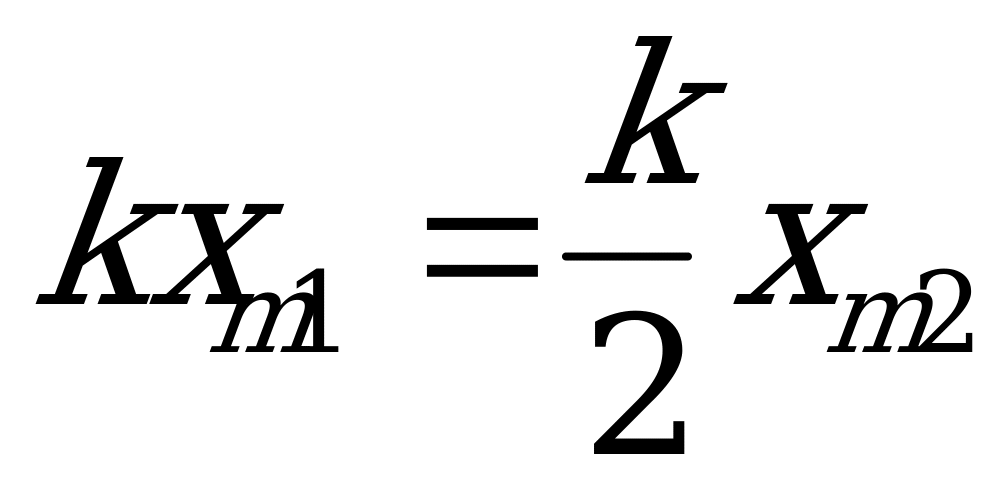

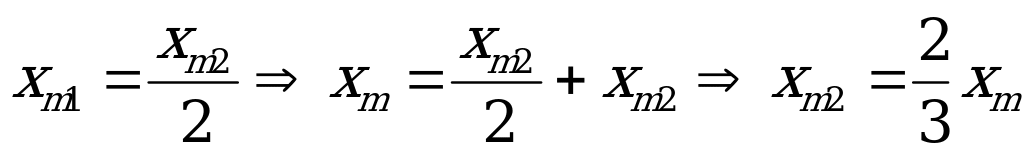 .
.
Поэтому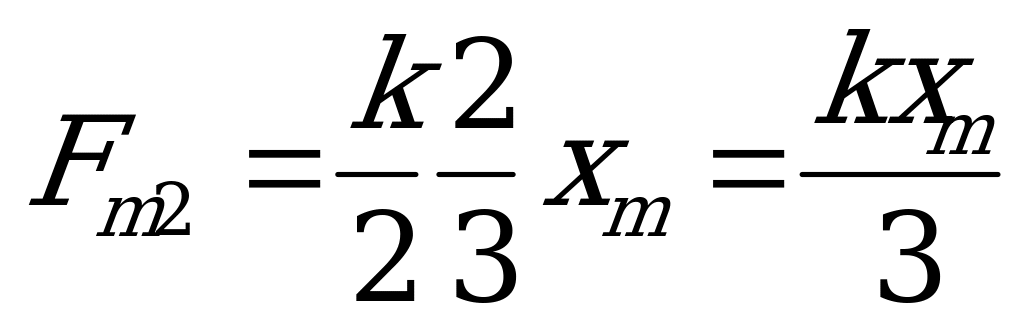 , что соответствует в задаче записи:
, что соответствует в задаче записи: 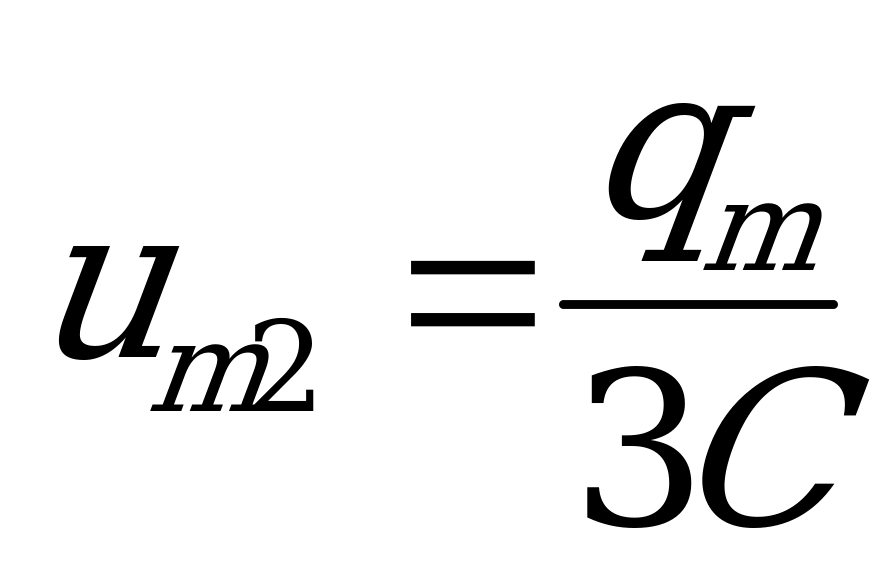 и новый период колебаний:
и новый период колебаний:
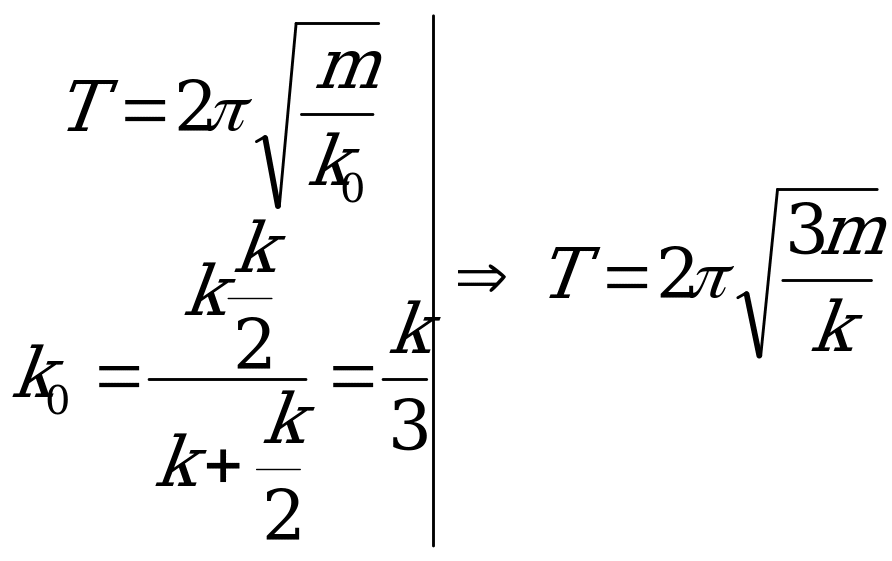 , что в задаче соответствует записи: T=2p
, что в задаче соответствует записи: T=2p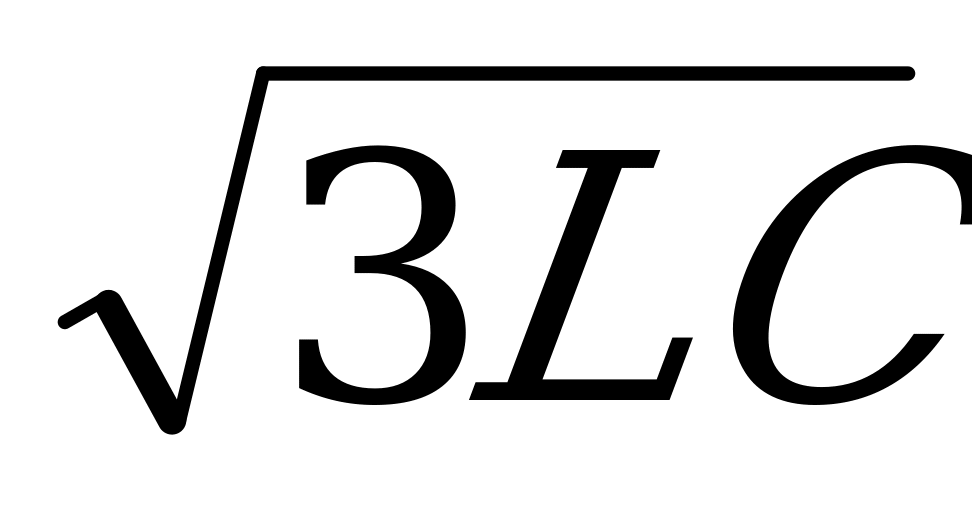
Задача 3.
Тело массы m совершает незатухающие колебания под действием максимальной силы Fm. В момент когда обе пружины полностью сжаты, точку О соединения пружин фиксируют. Найдите скорость тела через 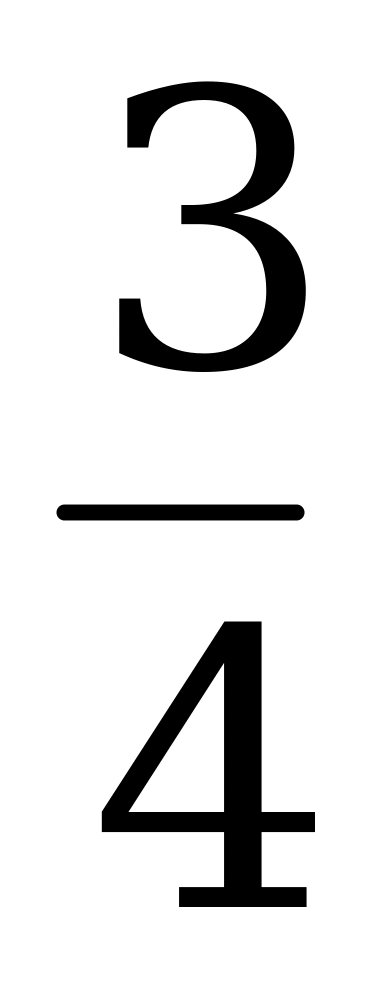 нового периода колебаний.
нового периода колебаний.
k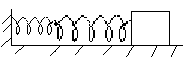 /2 k m
/2 k m
O
Решение 1.
На тело действует лишь пружина жесткостью k. Поэтому максимальная сила Fm=kxm действует в момент полного сжатия обеих пружин и xm – деформация пружины, прикрепленной к телу. В этот момент скорость тела равна нулю. Очевидно, что через 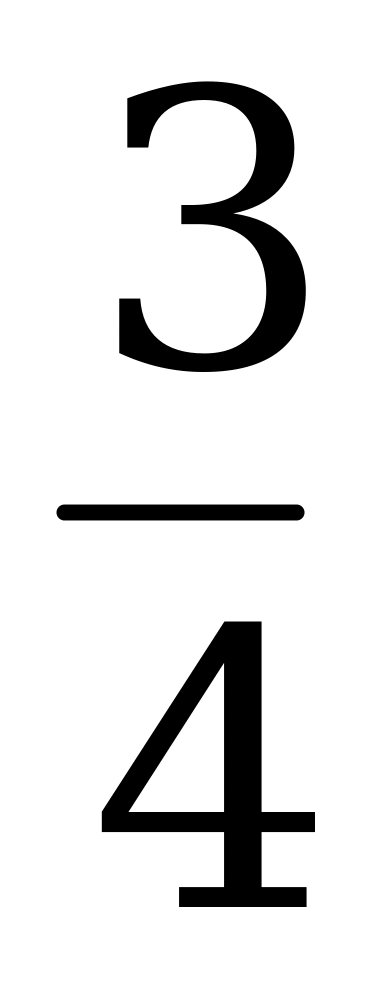 нового периода колебаний тело будет находиться в положении равновесия и значит иметь максимальную скорость. Воспользуемся законом сохранения энергии:
нового периода колебаний тело будет находиться в положении равновесия и значит иметь максимальную скорость. Воспользуемся законом сохранения энергии:
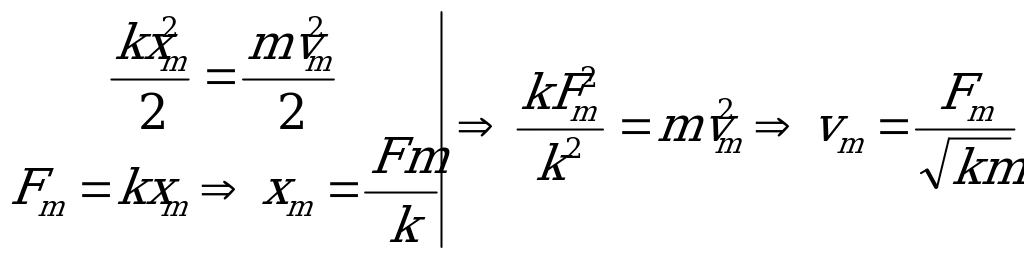
При переходе от механических к электромагнитным колебаниям решение становится настолько очевидным, что всякие рассуждения просто бессмысленны.
Решение 2.
2 C
C
C K
L
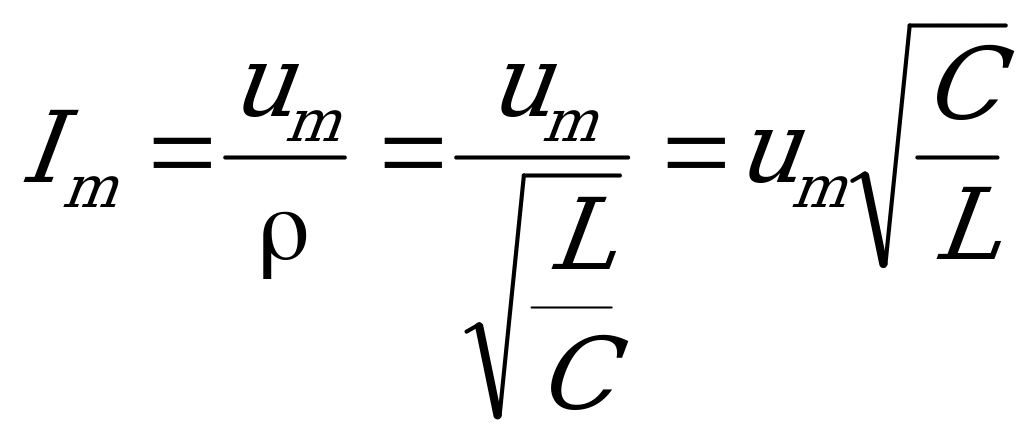 ,что в задаче соответствует записи
,что в задаче соответствует записи 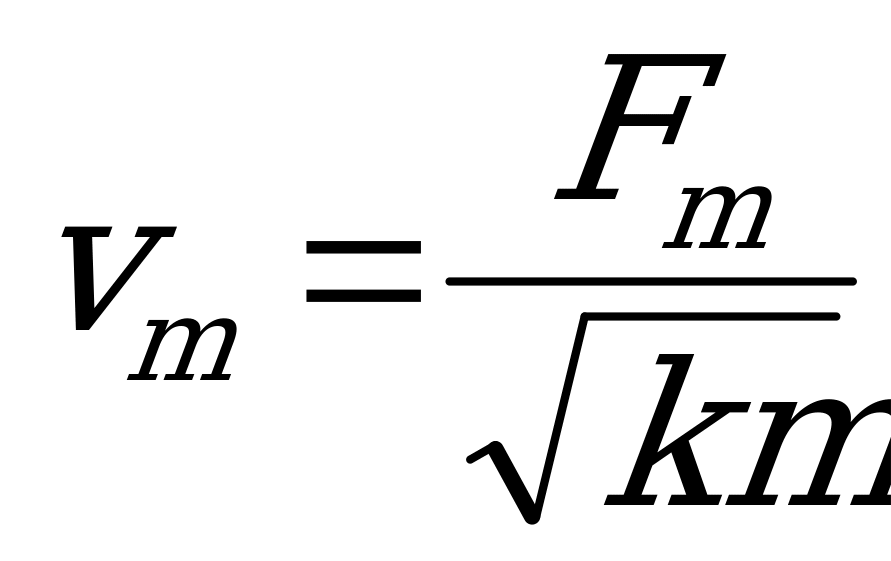
Задача 4.
Все тела – одной массы m, пружины – одинаковой жесткости k. Левая пружина сжата силой F и связана нитью. Найдите максимальную скорость первого тела после пережигания нити. Трение отсутствует.
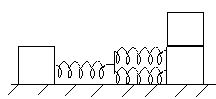
m k 3 m
k
1 2 m
k
После пережигания нити все три пружины практически мгновенно окажутся деформированными и лишь затем начнут действовать на тела. Эквивалентная жесткость пружин определяется из формулы:
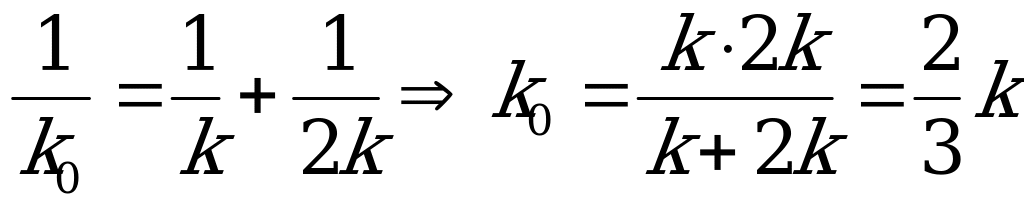
Новая сила упругости, действующая на тела со стороны пружин в первый момент равна: 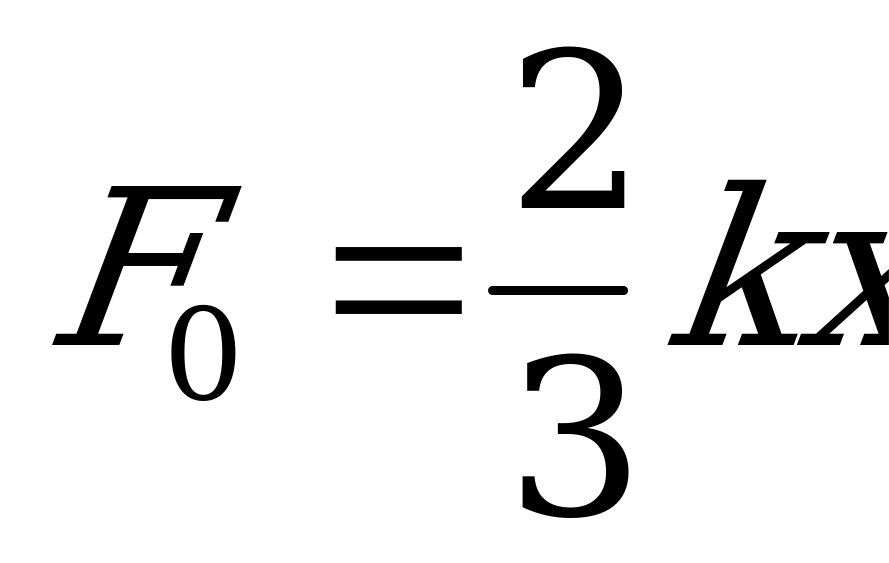 , где
, где 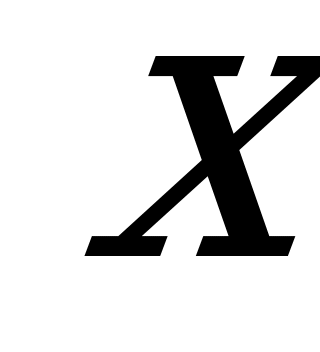 - суммарная деформация всех пружин. Очевидно, что она равна начальной деформации левой пружины, то есть
- суммарная деформация всех пружин. Очевидно, что она равна начальной деформации левой пружины, то есть 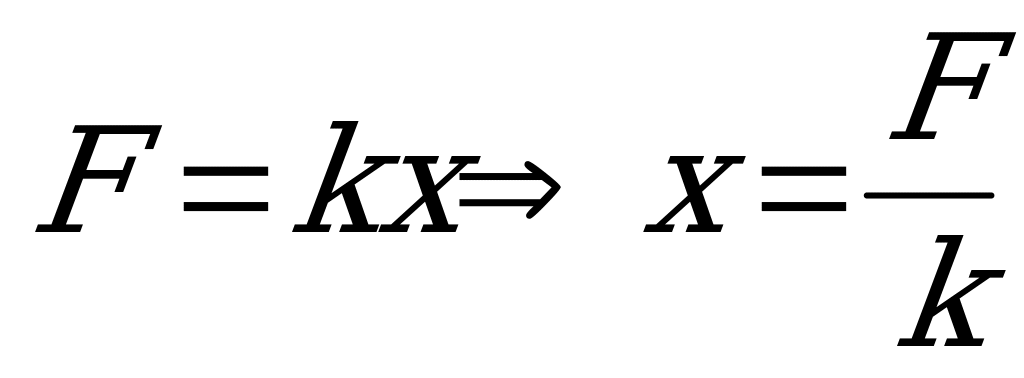 и
и 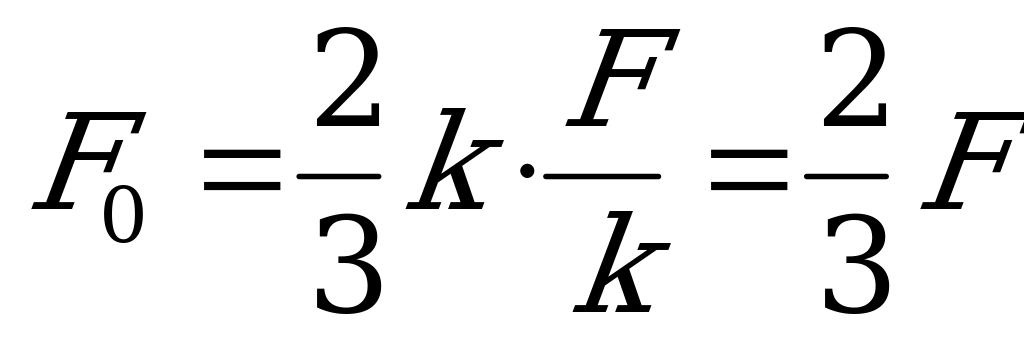 .
.
Согласно закону сохранения импульса, первое тело будет совершать колебания относительно центра масс под действием пружины некоторой жесткости 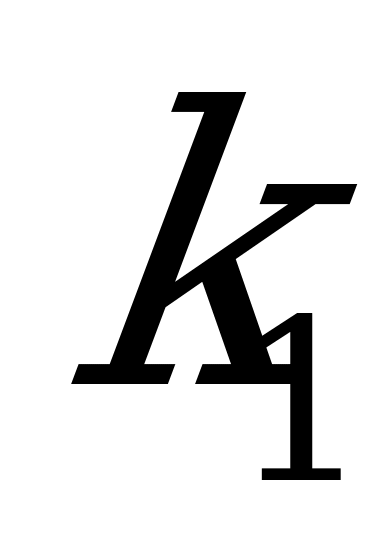 . Так как частоты колебаний тел 1 и 2+3 – одинаковы, то:
. Так как частоты колебаний тел 1 и 2+3 – одинаковы, то:
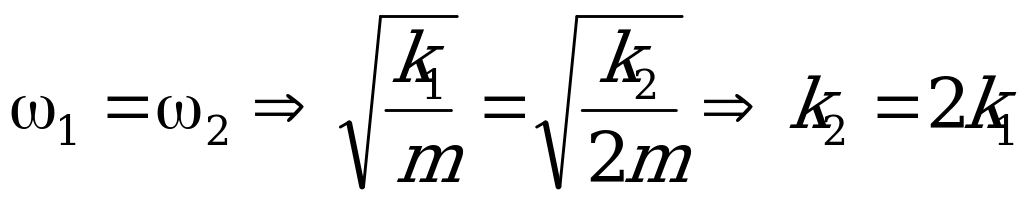 и
и 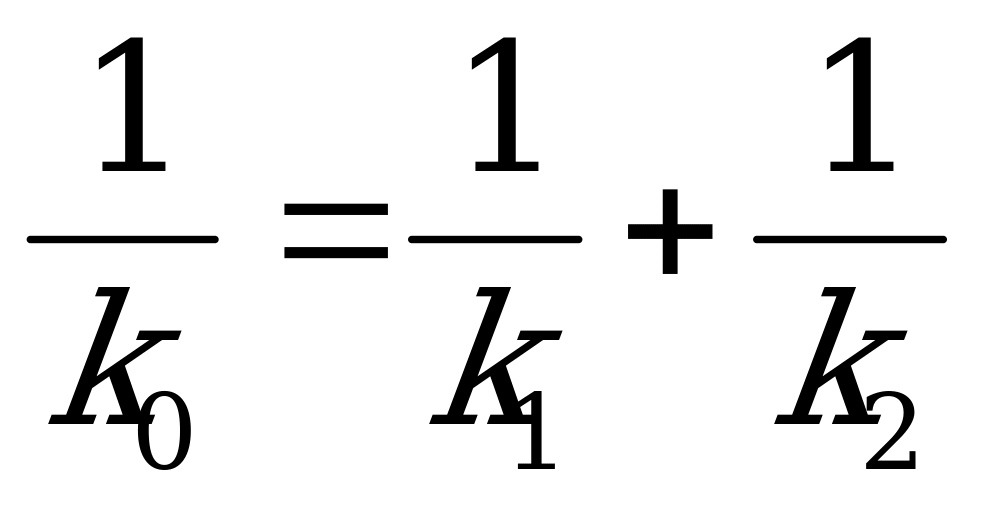
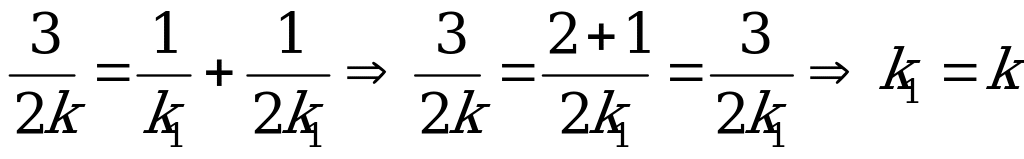 .
.
Запишем закон сохранения энергии, используя соотношение: 
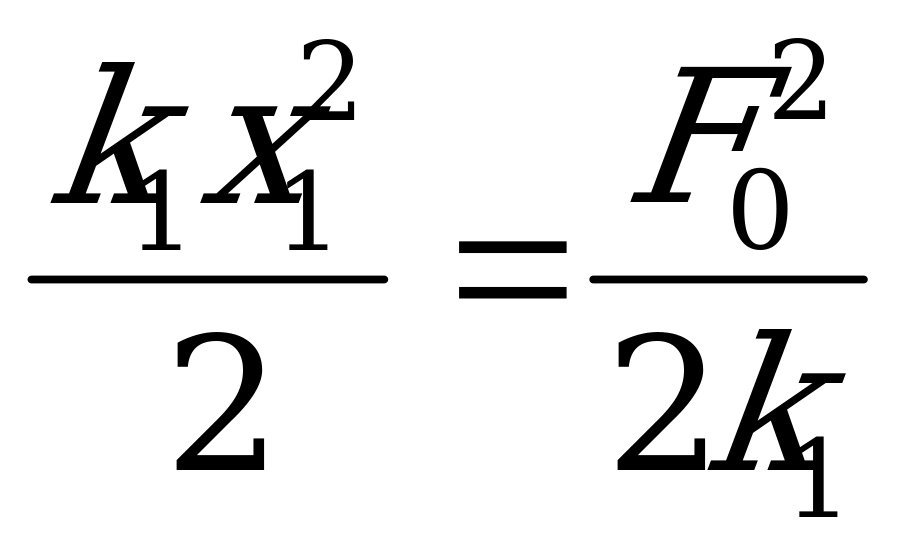 и, принимая во внимание, что
и, принимая во внимание, что 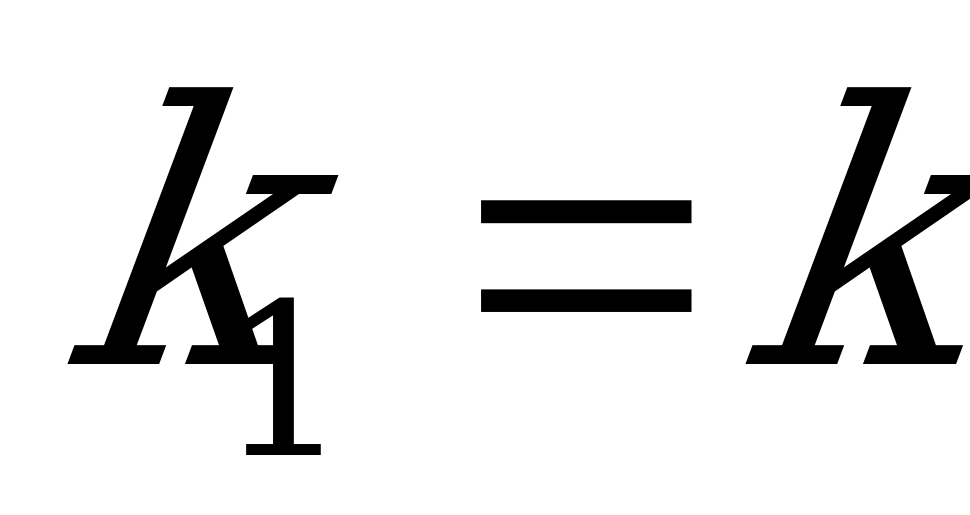 и
и 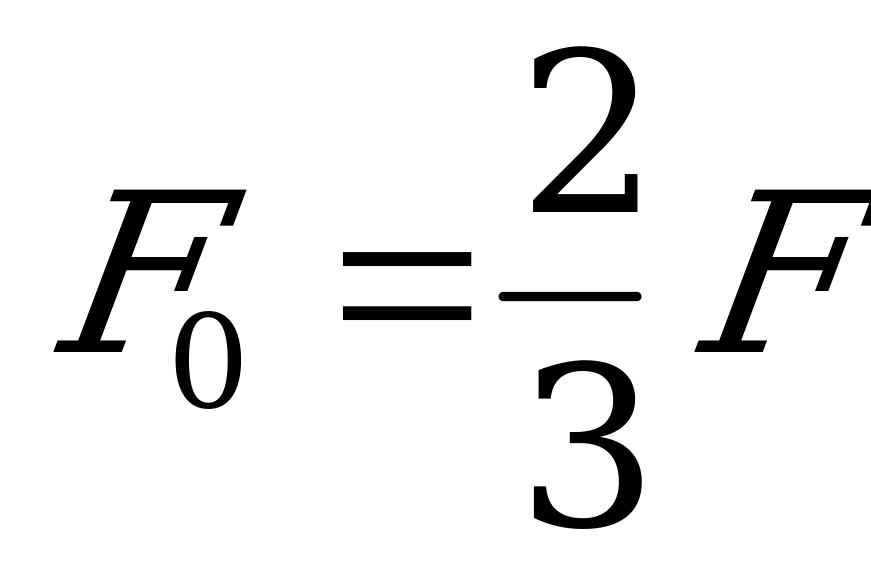
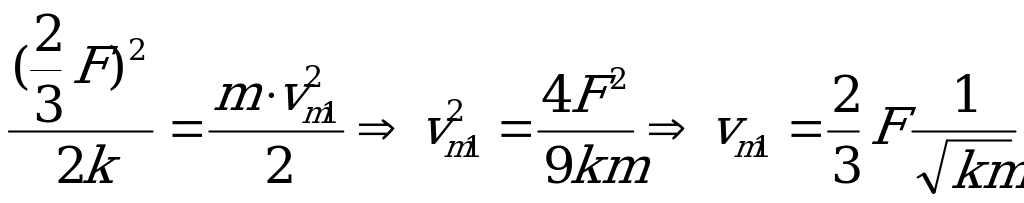
Решение оказывается проще при переходе от механических к электромагнитным колебаниям.
Решение 2.
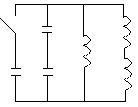
K C 2 L
1 L
U, C C 3 L
Надо найти максимальный ток через катушку 1 после замыкания ключа К. Очевидно, что этот ток равен 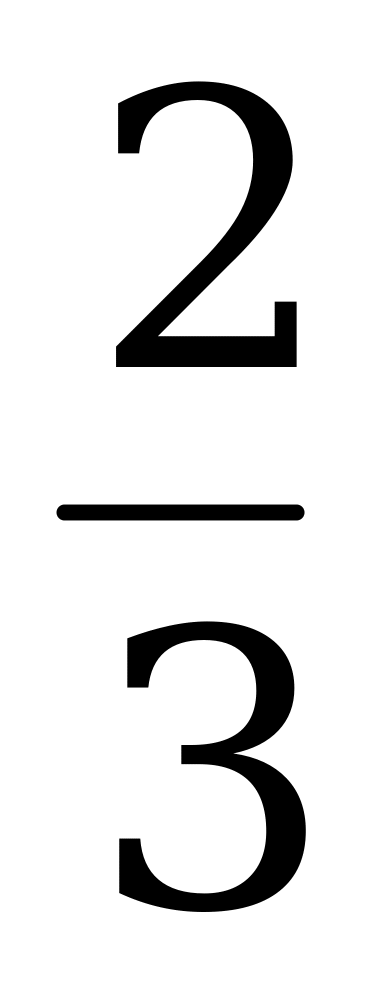 от общего тока через все катушки, так как ток обратно пропорционален сопротивлению
от общего тока через все катушки, так как ток обратно пропорционален сопротивлению 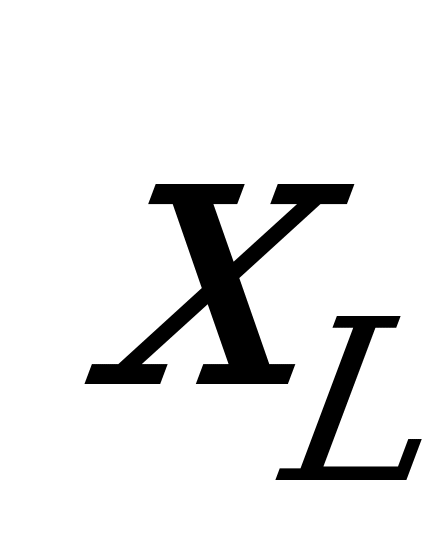 , которое в свою очередь пропорционально индуктивности:
, которое в свою очередь пропорционально индуктивности: 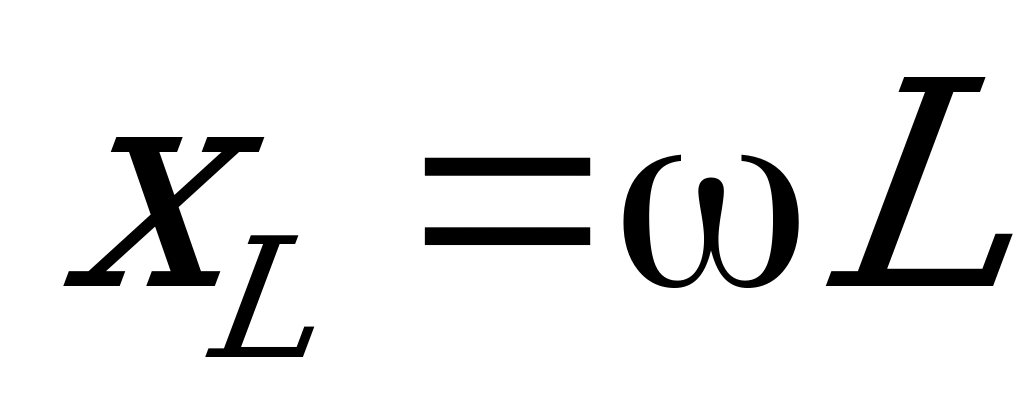
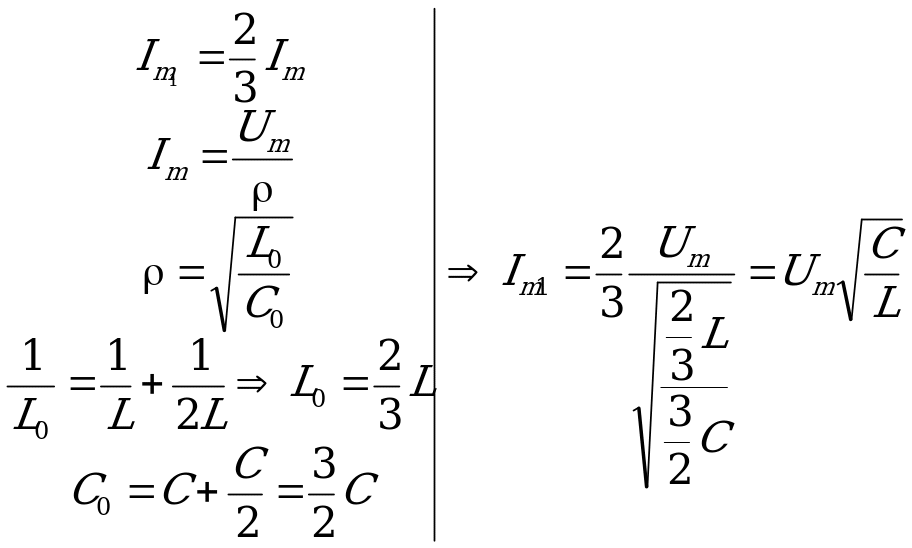
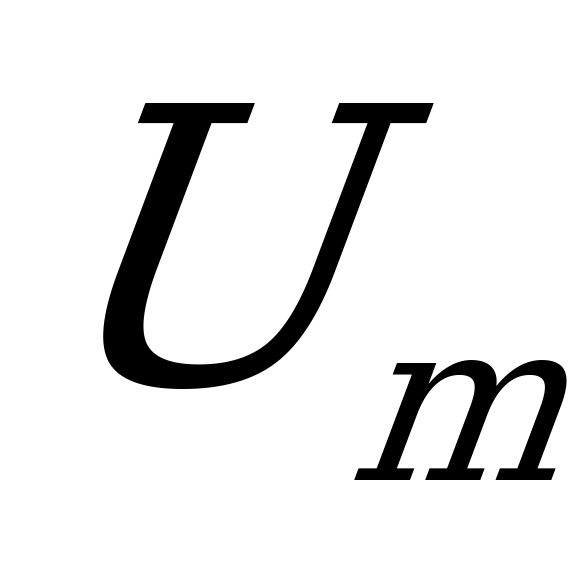 найдем из закона сохранения заряда:
найдем из закона сохранения заряда: 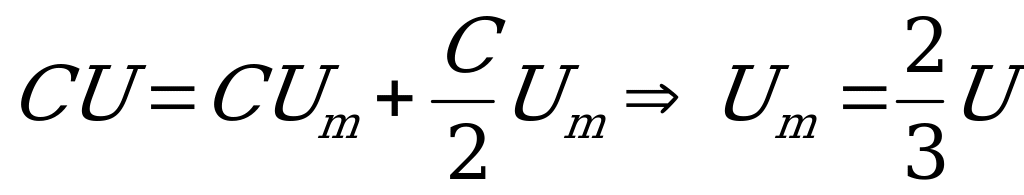
И окончательно имеем: 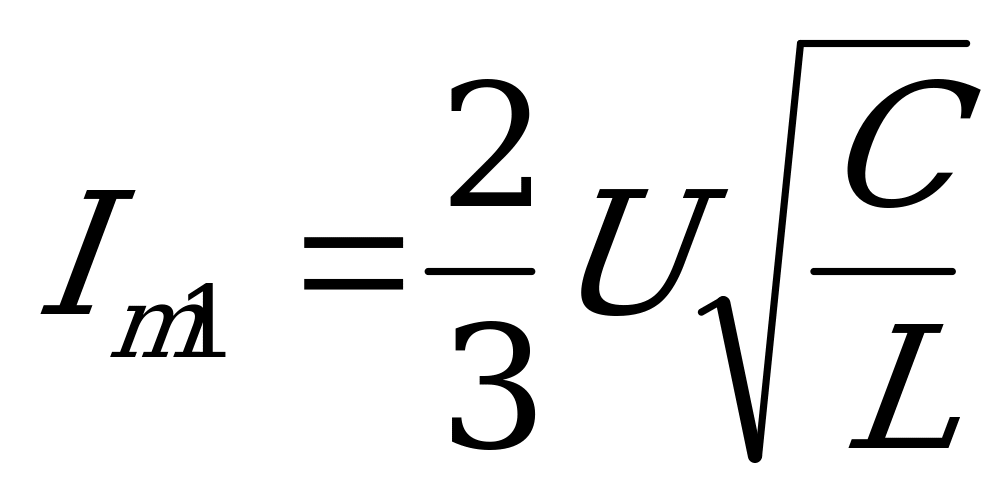 , что в задаче соответствует записи:
, что в задаче соответствует записи:
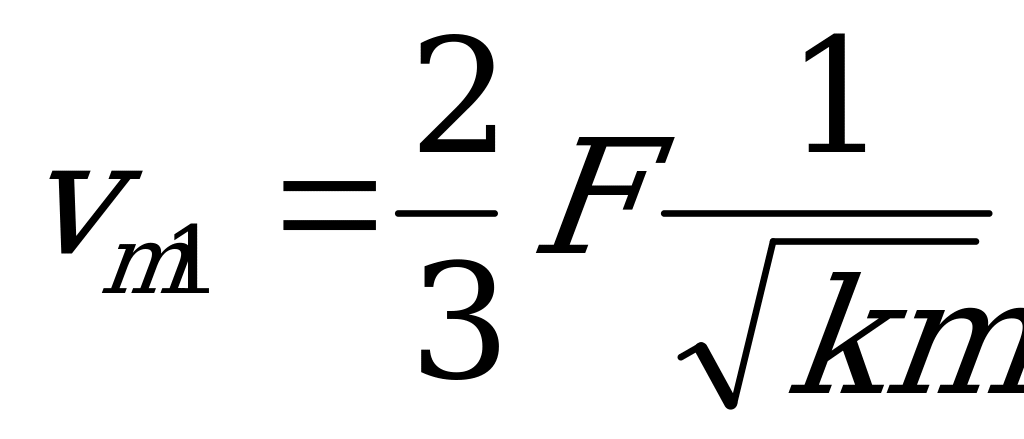 .
.
Задача 5.
В колебательном контуре происходят незатухающие колебания. Когда сила тока в катушке 1 достигает максимального значения 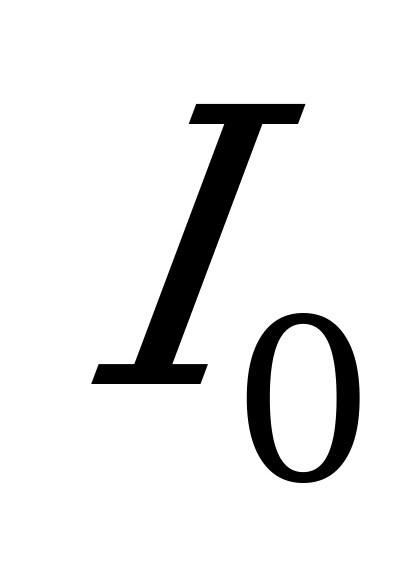 , в неё быстро (за время, малое по сравнению с периодом колебаний) вставляют сердечник, что приводит к увеличению её индуктивности в
, в неё быстро (за время, малое по сравнению с периодом колебаний) вставляют сердечник, что приводит к увеличению её индуктивности в 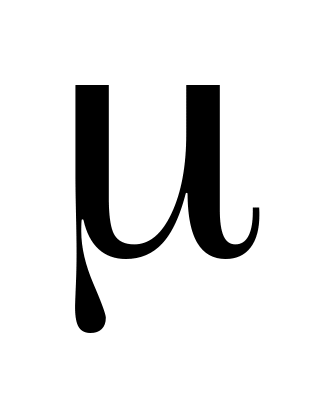 раз. Определите максимальное напряжение на конденсаторе после вставки сердечника.
раз. Определите максимальное напряжение на конденсаторе после вставки сердечника.
C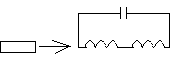
L1 L2
Решение осложняется тем, что неясно, будет ли работать закон сохранения энергии магнитного поля или нет. Однако как следует из аналогии электромагнитных и механических колебаний, в которых закон сохранения импульса 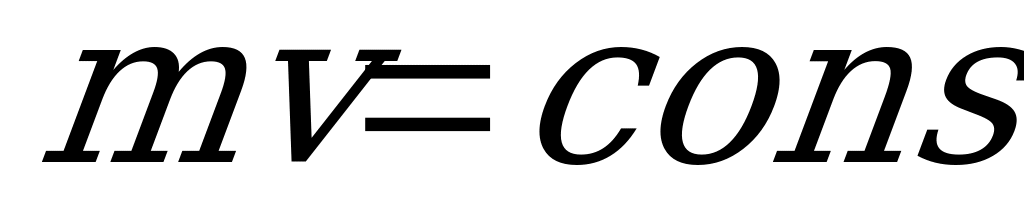 выполняется всегда, в электромагнитной системе должен выполняться следующий закон сохранения:
выполняется всегда, в электромагнитной системе должен выполняться следующий закон сохранения: 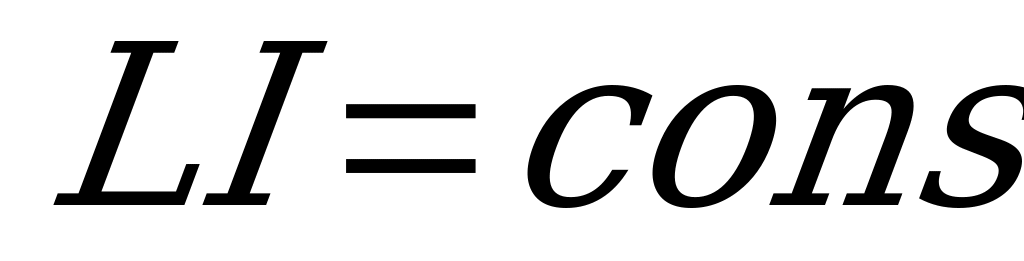 или
или 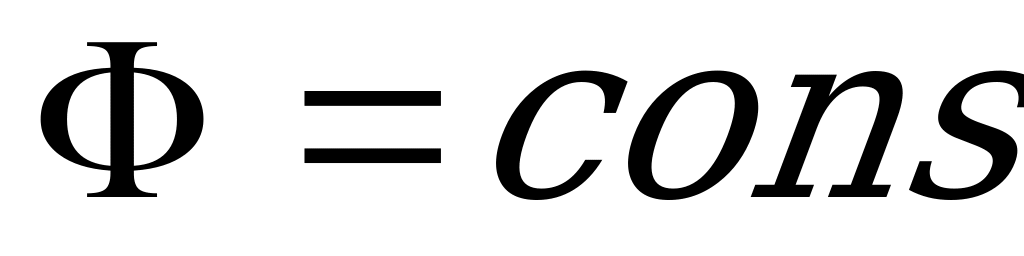 ,то есть имеет место закон сохранения магнитного потока.
,то есть имеет место закон сохранения магнитного потока.
Решение 1.
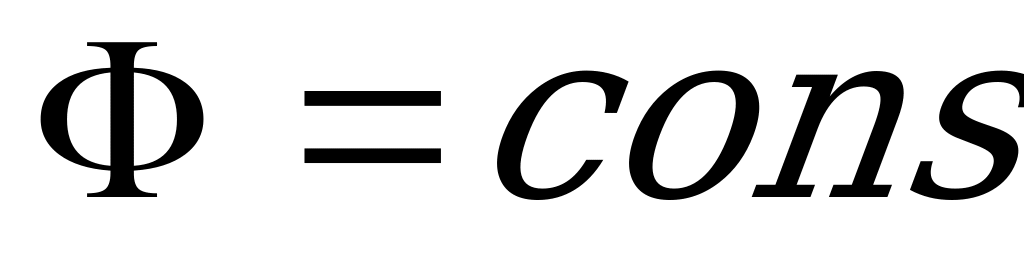
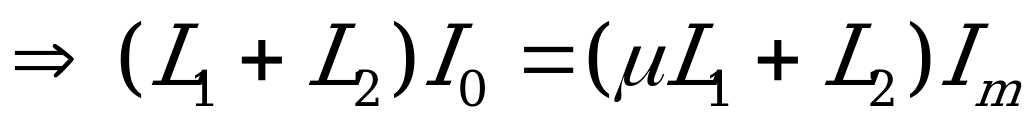 ,где
,где 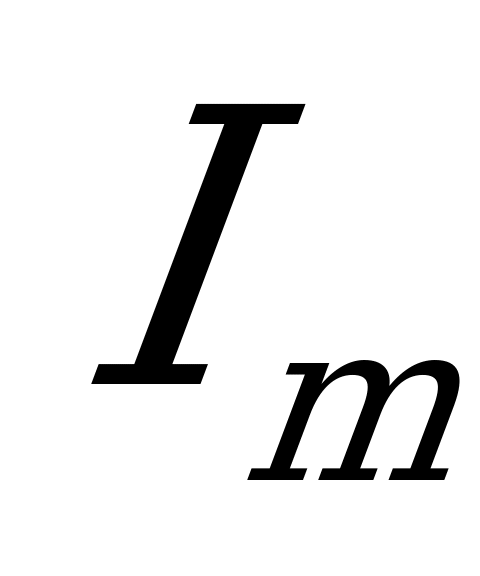 – новый максимальный ток через катушки
– новый максимальный ток через катушки 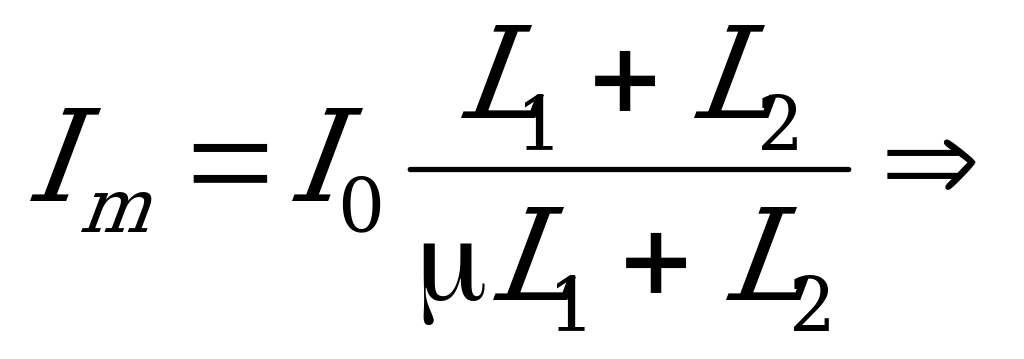 по закону сохранения энергии после того как сердечник вставлен в катушку:
по закону сохранения энергии после того как сердечник вставлен в катушку:
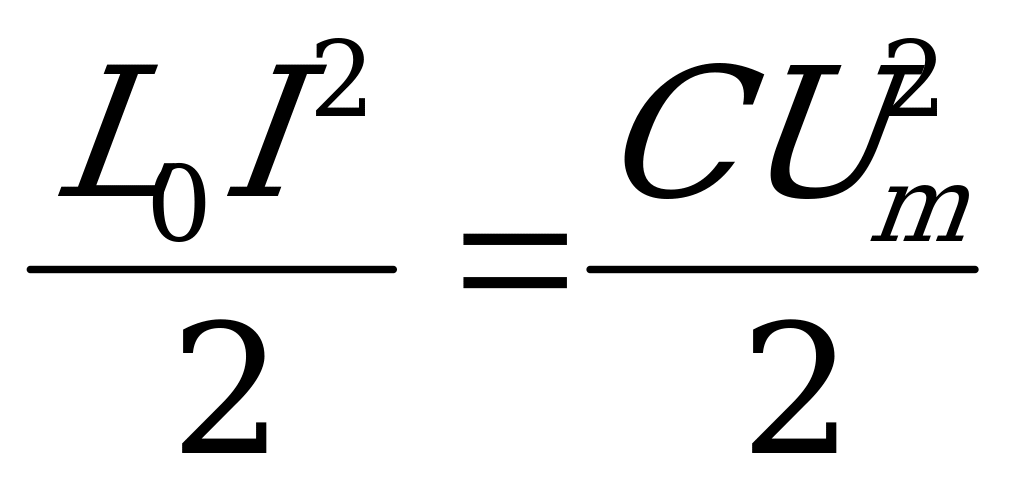
или
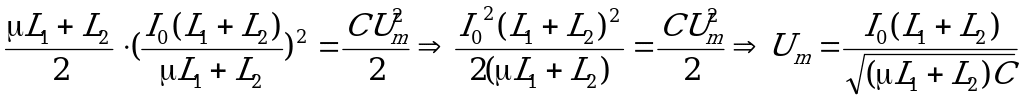
Решение 2.
m1
k
m2
При переходе в механическую систему в момент, когда грузы имеют максимальную скорость 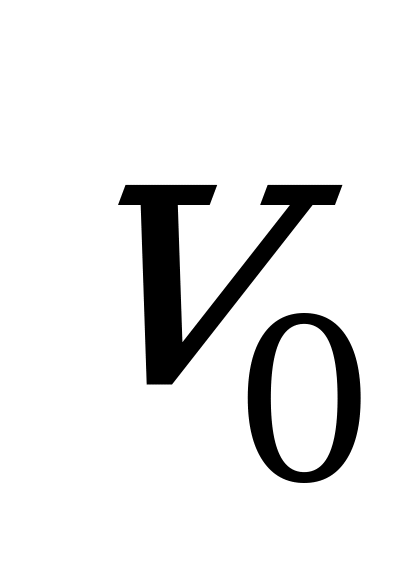 , на груз массы
, на груз массы 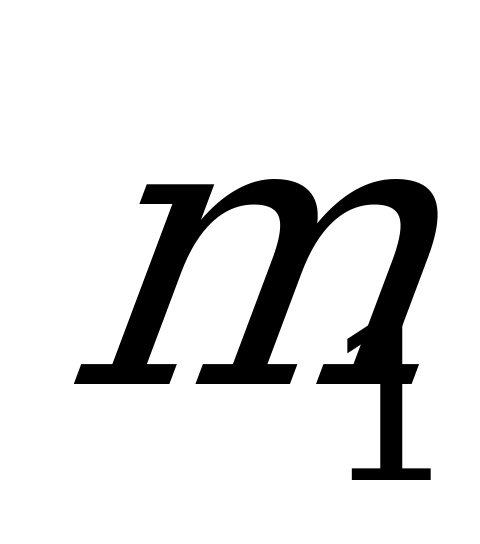 ставят без начальной скорости перегрузок
ставят без начальной скорости перегрузок 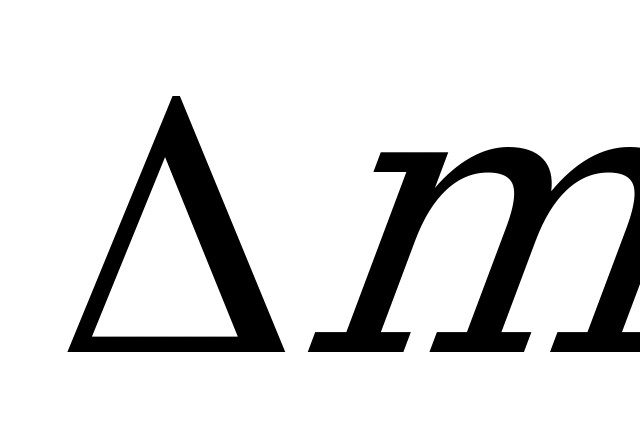 , такой массы, что их суммарная масса увеличивается в
, такой массы, что их суммарная масса увеличивается в 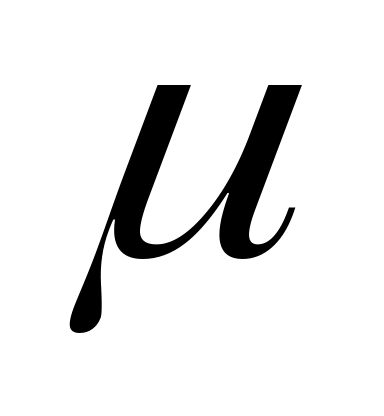 раз:
раз: 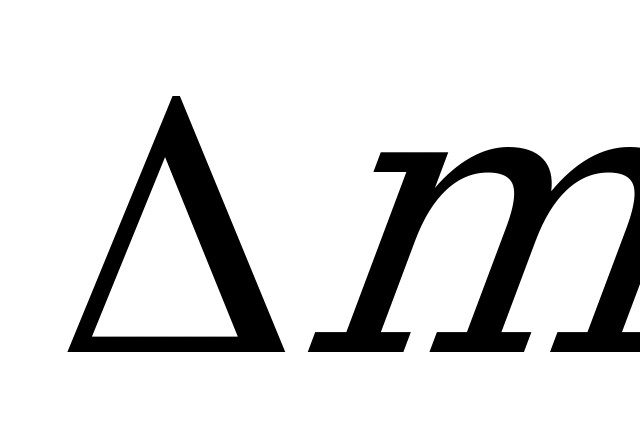 +
+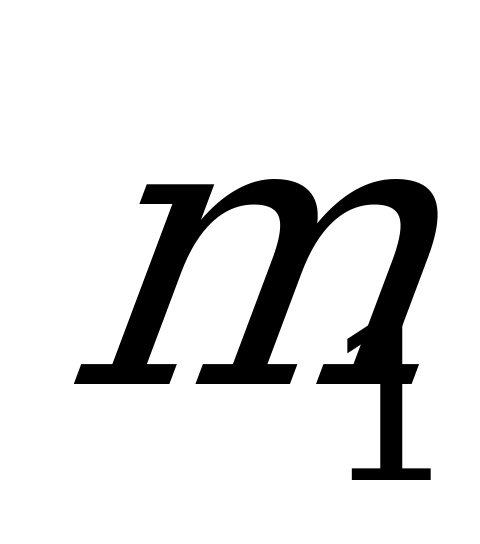 =
=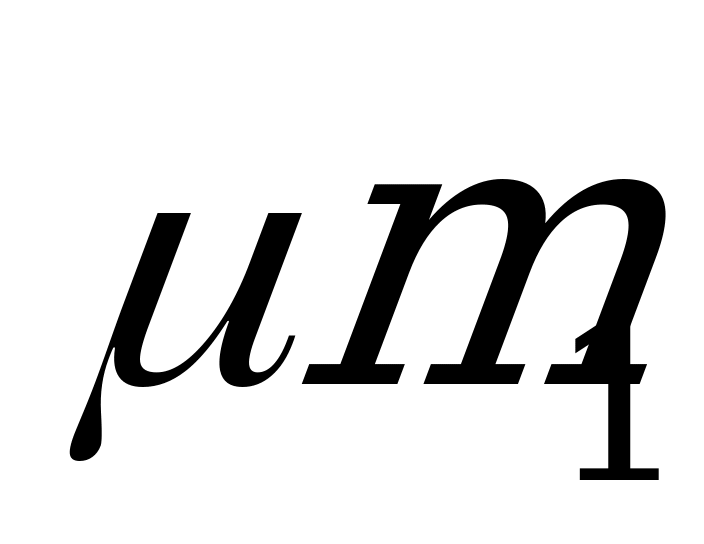 , что соответствует неупругому удару. Следовательно, закон сохранения механической энергии не выполняется! По закону сохранения импульса:
, что соответствует неупругому удару. Следовательно, закон сохранения механической энергии не выполняется! По закону сохранения импульса:
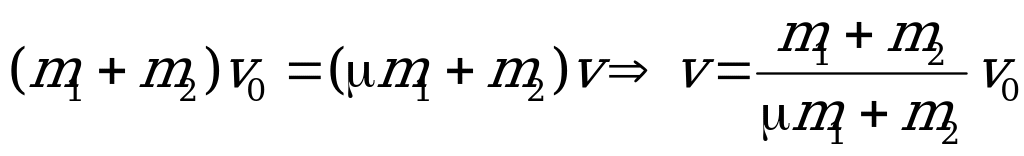 .
.
И по закону сохранения энергии после того, как груз поставлен:
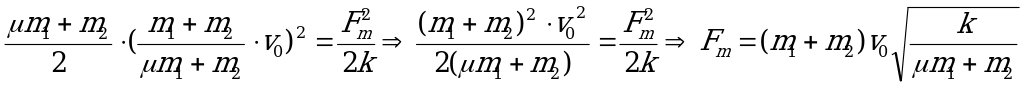 ,
,
что в задаче соответствует записи:
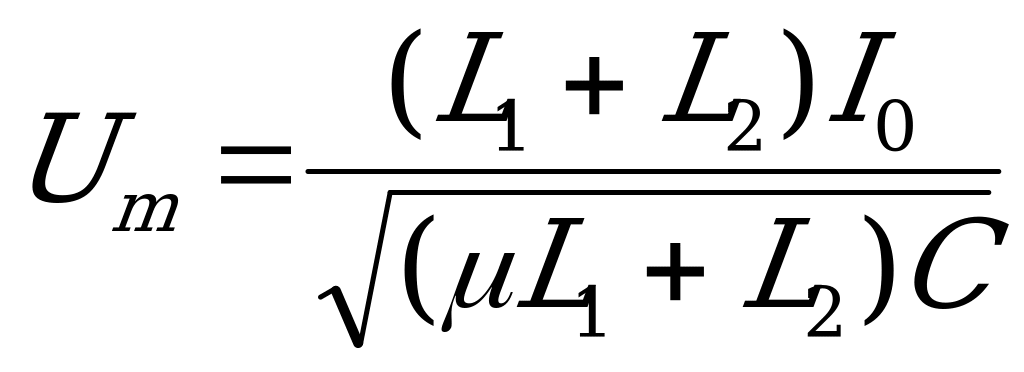
Задача 6.
Цепь первоначально разомкнута и конденсатор С1 заряжен до напряжения U1, а конденсатор С2 остается незаряженным. Определите максимальную величину силы тока в цепи после замыкания ключа К.
 L
L
U1,C1 C2 K
Решение данной задачи с использованием законов сохранения заряда и энергии займет более страницы. Поэтому попробуем ее решить двумя простыми способами, каждый из которых основывается на переходе в механическую систему.
Решение 1.
П ерейдем в механическую систему.
ерейдем в механическую систему.
k1 m
k2
Одна из параллельно соединенных пружин сжата и связана нитью. После разрезания нити тело начинает совершать колебания. Очевидно, что максимальная сила, которая будет действовать на тело, равна силе упругости, с которой была первоначально сжата пружина жесткостью k1.
Тогда по второму закону Ньютона
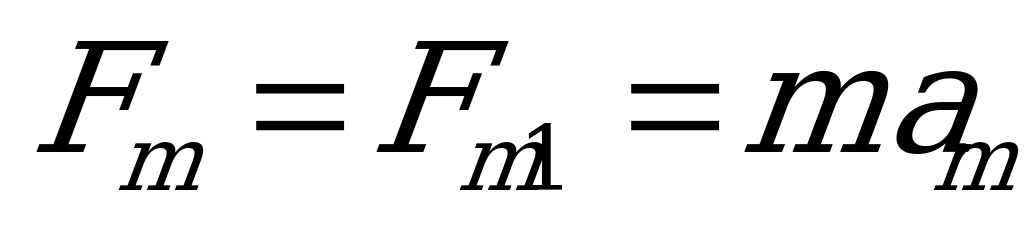 ,но
,но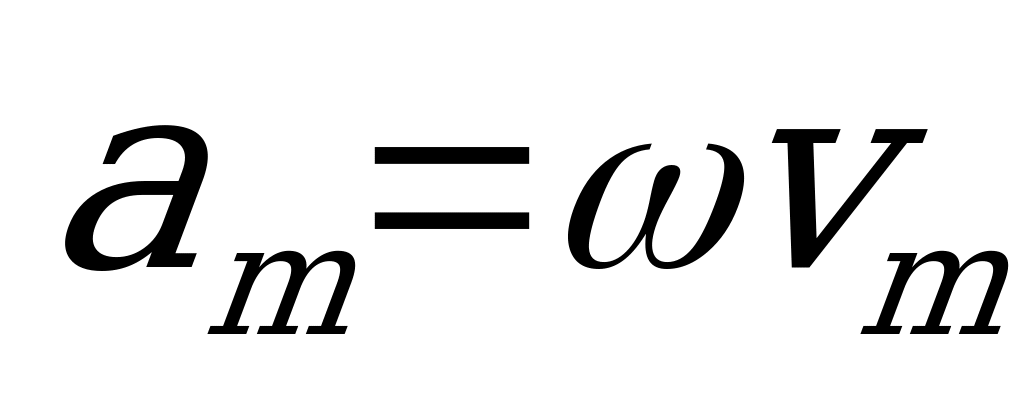 и
и
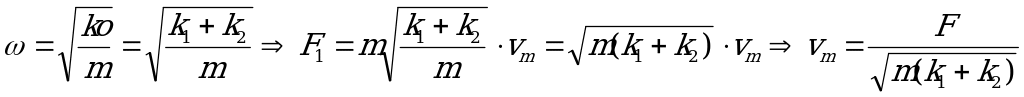 ,
,
что в задаче соответствует записи:
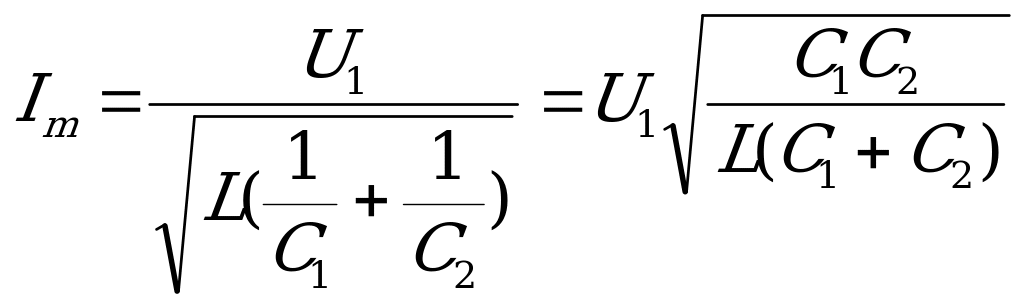
Решение 2.
При рассмотрении механической модели легко выясняется, что Fm=F1,а значит Um после замыкания ключа в электромагнитной схеме равно U1. тогда
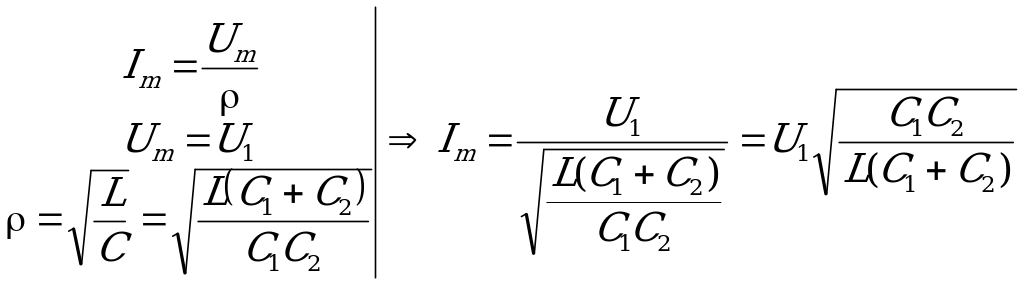
Задача 7.
Одна из пружин жесткостью k сжата силой F и связана нитью. Каков будет период колебаний грузов и какова их максимальная скорость после разрезания нити.
m k k 2m
k k 2m
k/2
Приводить решение этой задачи без перехода в электромагнитную систему просто не имеет смысла, так как оно слишком громоздко. Поэтому сразу перейдем к электромагнитной системе.
Решение.
U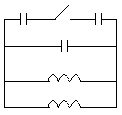 ,C K 2C
,C K 2C
C
L
2L
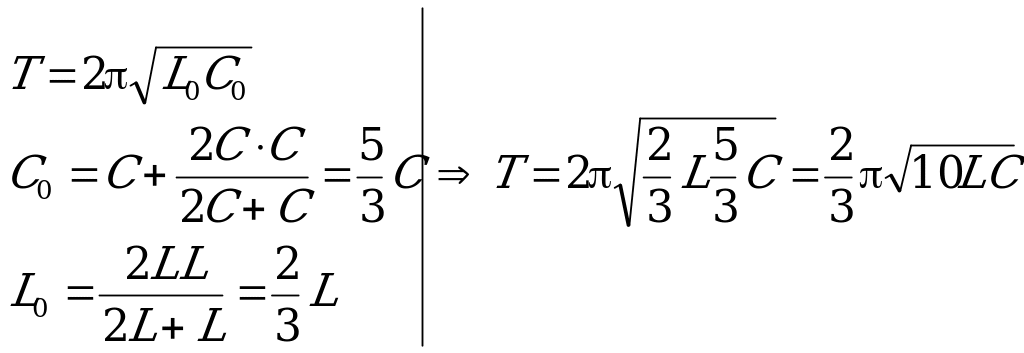 ,
,
что в задаче соответствует записи: 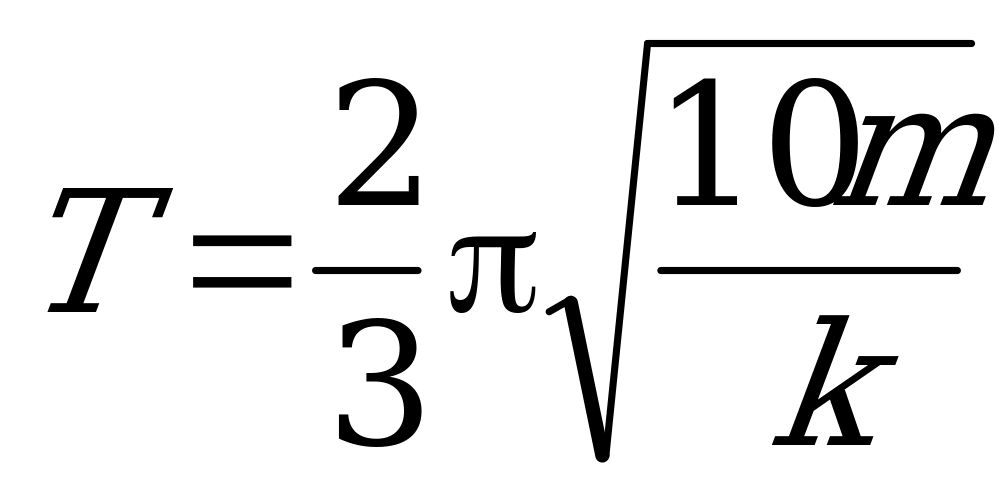
Максимальный ток через катушки найдем по закону сохранения заряда и энергии после замыкания ключа К:
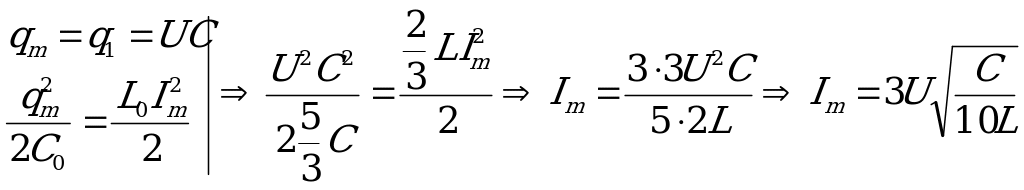
Точки в катушках будут делиться обратно пропорционально их индуктивности и значит
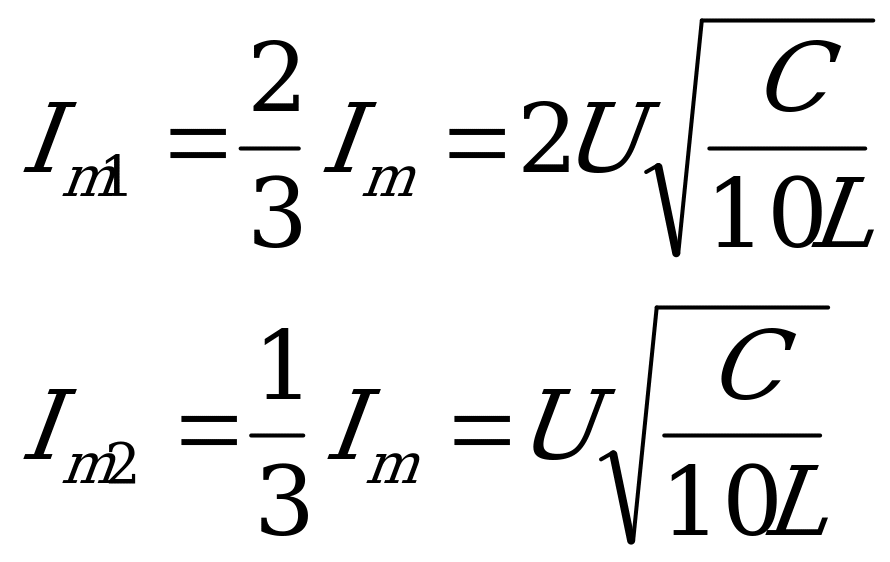 ,
,
что в задаче соответствует записи:
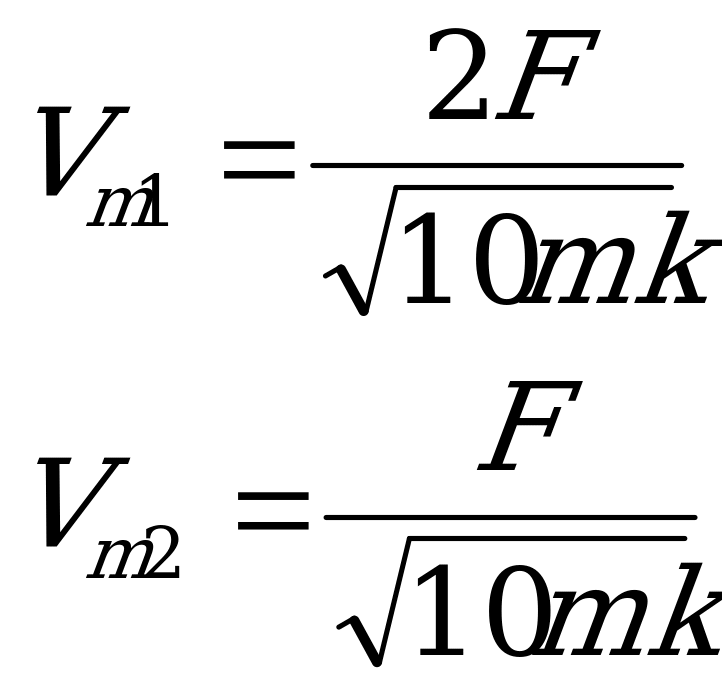
Метод аналогий может быть использован не только в колебаниях, но и при решении других физических проблем. Например, возможно введение силовой и энергетической характеристики любого потенциального поля, такого, скажем, как поле сил инерции. Тогда сложные задачи, в которых используют центробежные силы или силы Кориолиса, сводятся к простым, решаемым с помощью закона сохранения энергии.








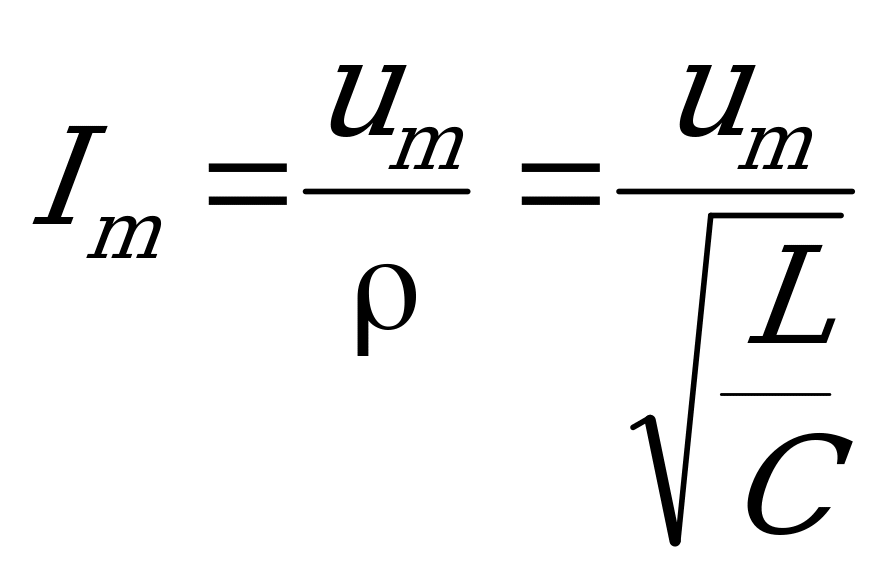 , где
, где 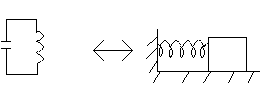 m
m 1 k2
1 k2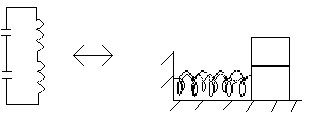
 1 k m2
1 k m2 1
1
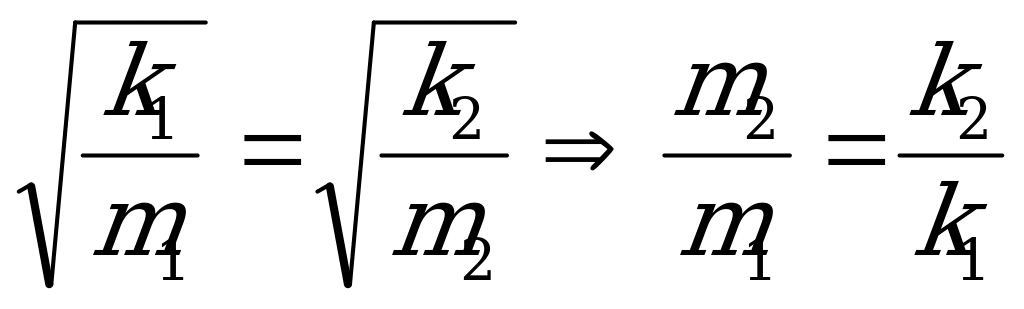
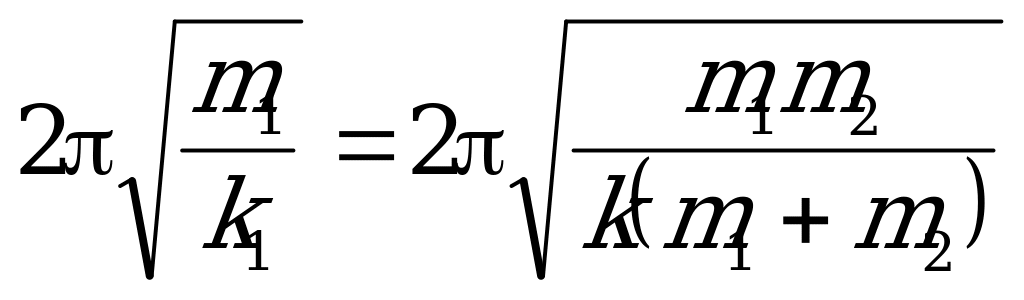
 L1 L2
L1 L2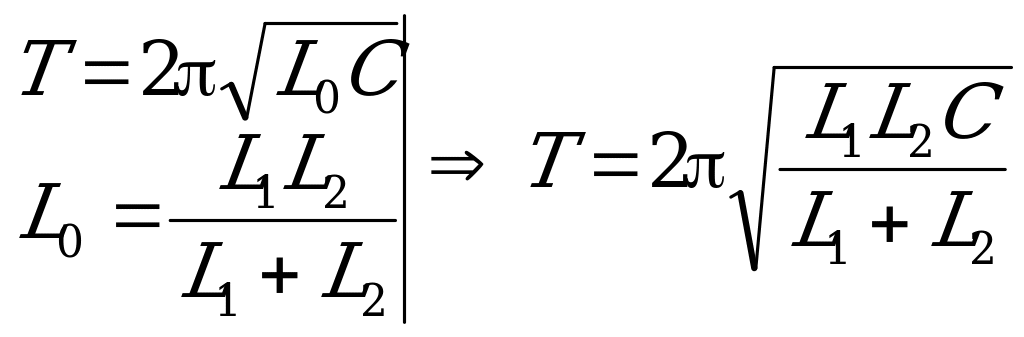 , что в задаче соответствует записи
, что в задаче соответствует записи 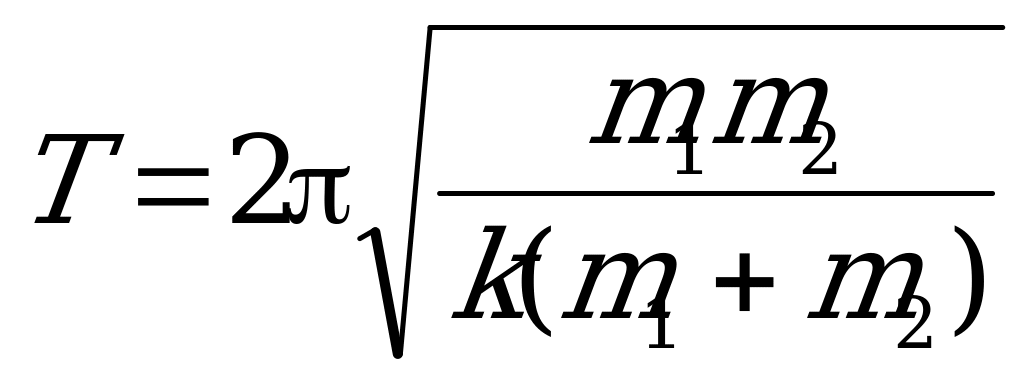
 C
C /2 k m
/2 k m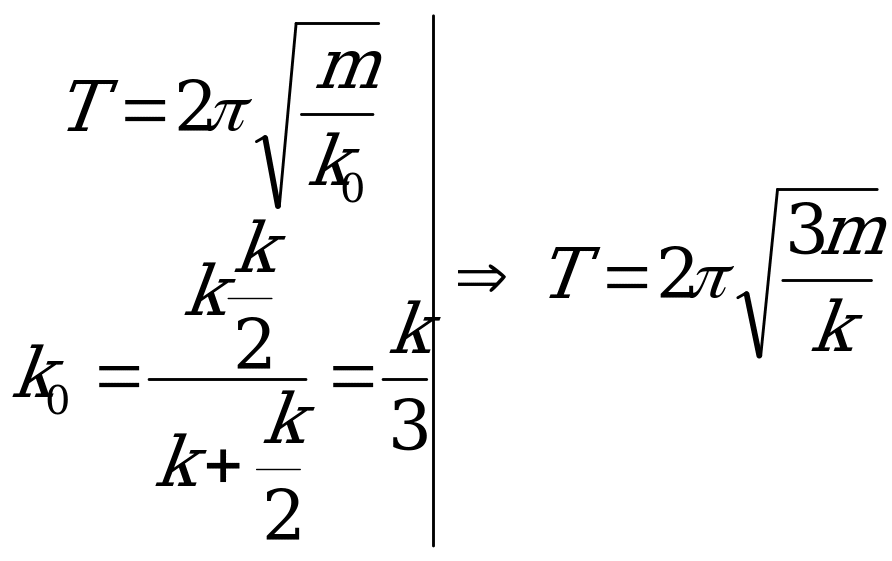 , что в задаче соответствует записи: T=2p
, что в задаче соответствует записи: T=2p /2 k m
/2 k m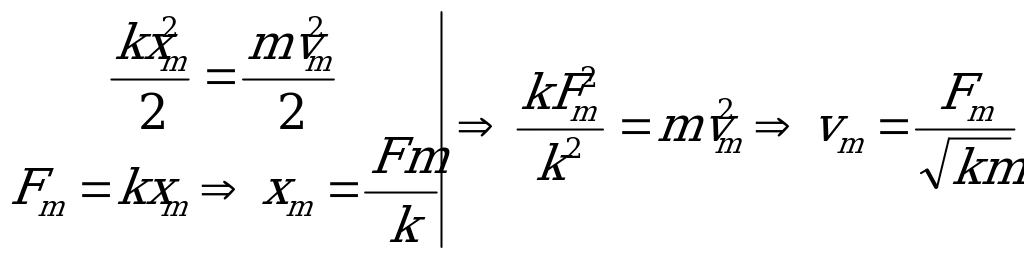
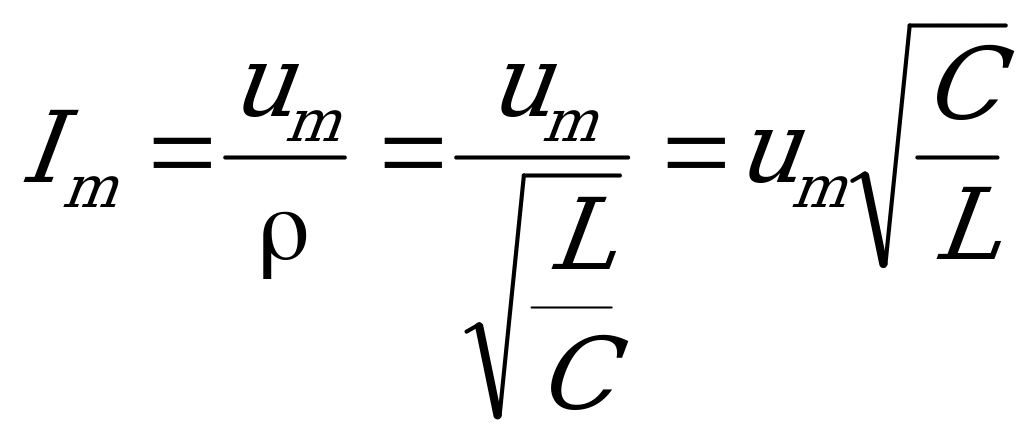 ,что в задаче соответствует записи
,что в задаче соответствует записи 
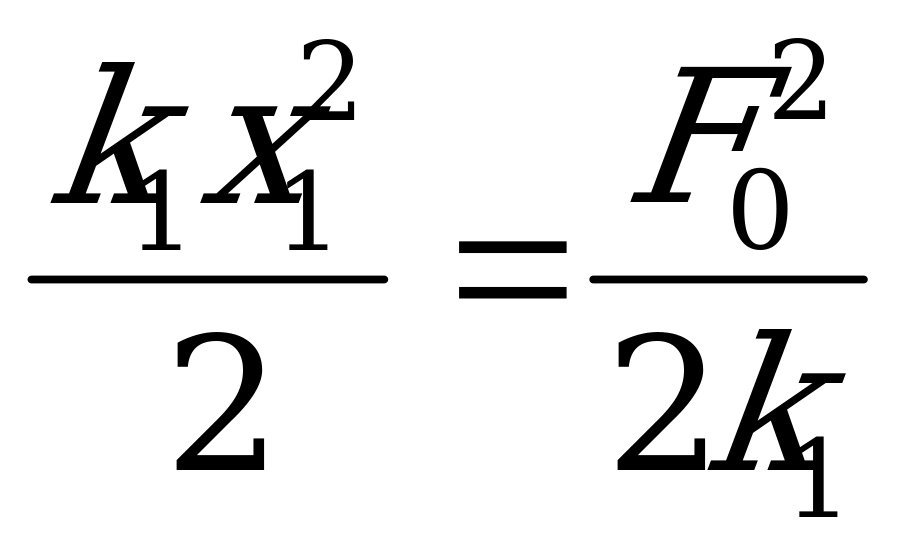 и, принимая во внимание, что
и, принимая во внимание, что 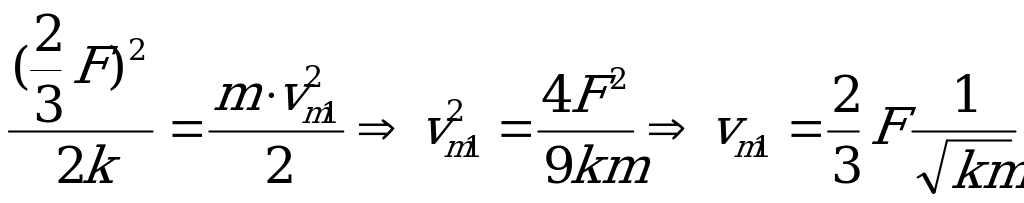

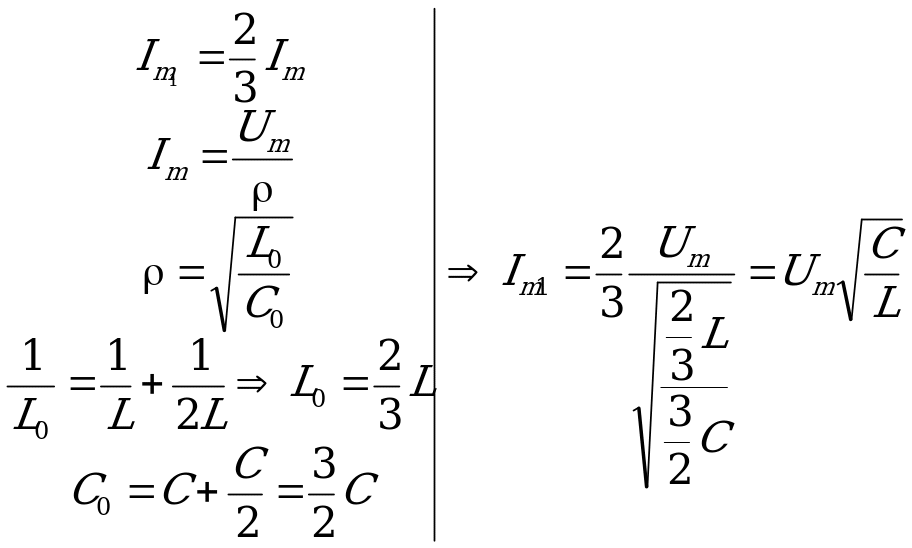

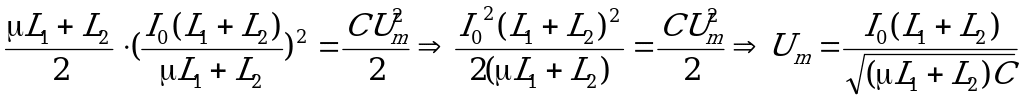

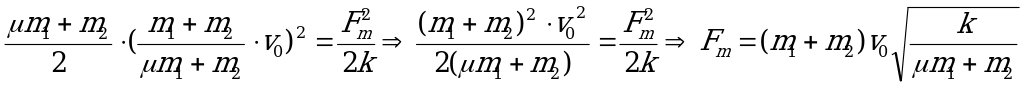 ,
, L
L ерейдем в механическую систему.
ерейдем в механическую систему.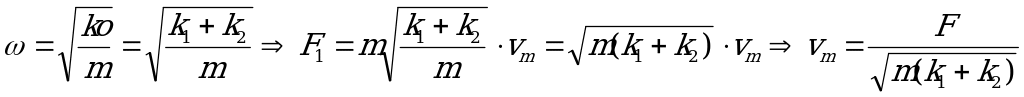 ,
,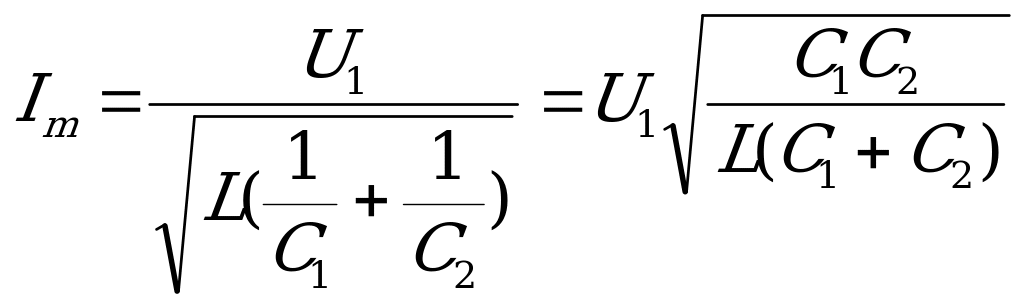
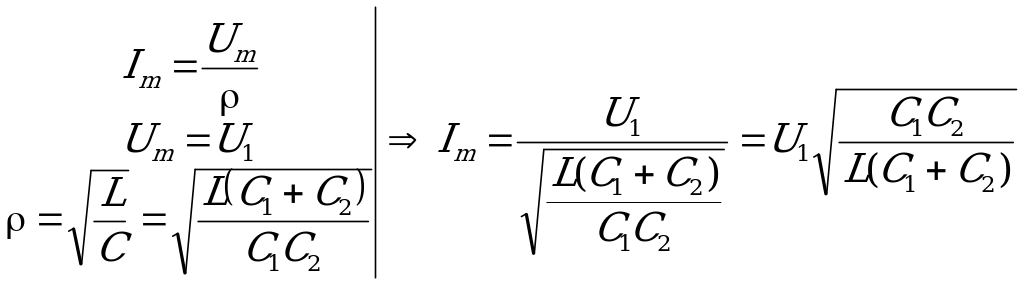
 k k 2m
k k 2m ,C K 2C
,C K 2C 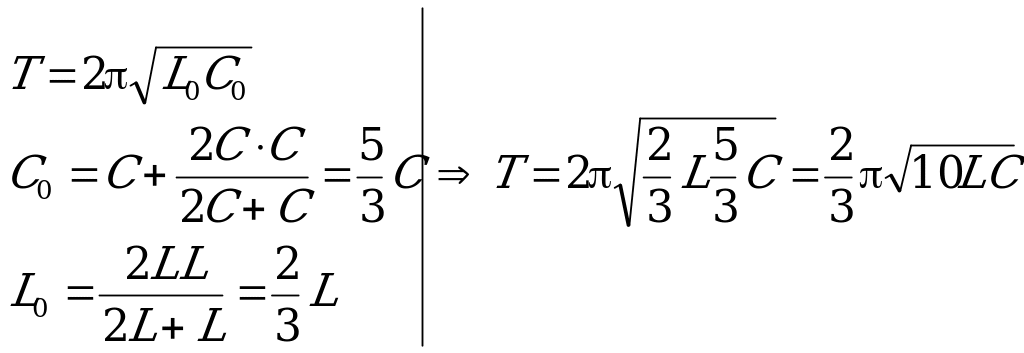 ,
,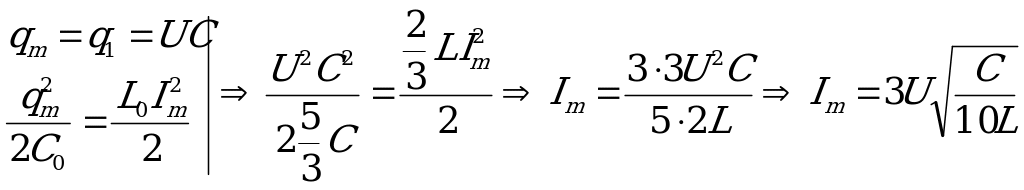
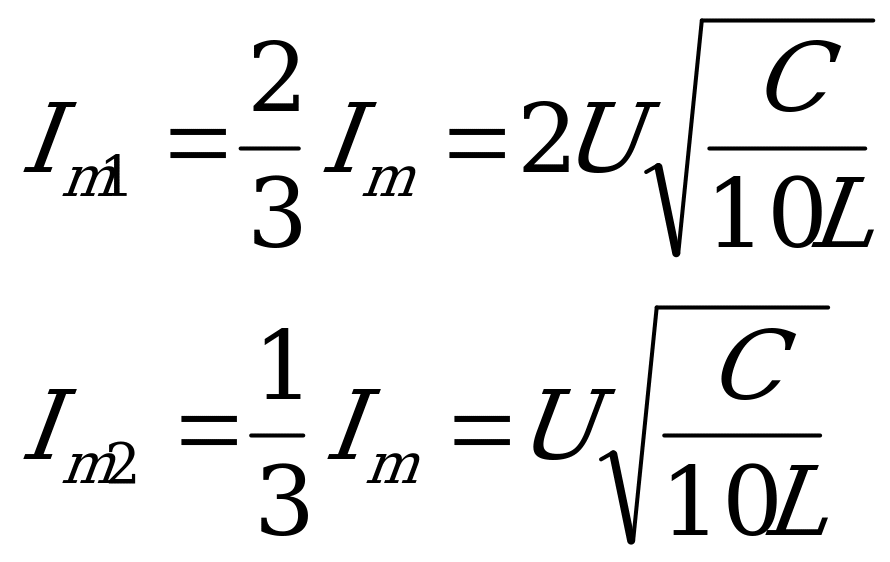 ,
,