"Геометрические преобразования пространства в ландшафтном дизайне" (презентация для студентов обучающихся по специальности "Ландшафтный дизайнер")

Геометрические преобразования пространства в ландшафтном дизайне

Автор презентации: Шмат Наталья Владимировна

Преподаватель математики ГБПОУ МО «Щелковский колледж»

Презентация для студентов обучающихся по специальности «Ландшафтный дизайнер»

«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе» Л.Н. Толстой

Примеры симметрии

Примеры симметрии

симметрия в ландшафтном дизайне

симметрия в ландшафтном дизайне

симметрия в ландшафтном дизайне

Геометрические преобразования пространства

определение геометрического преобразования и движения

• В геометрии выделяют геометрические преобразования, сохраняющие расстояния между соответствующими точками. Такие геометрические преобразования называются движениями.

• Если каждую точку данной фигуры на плоскости или в пространстве сместить каким-нибудь образом, то получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.

рассмотрим геометрические преобразования:

1) Центральная симметрия;

2) Осевая симметрия;

3) Зеркальная симметрия;

2) Параллельный перенос;

3) Поворот.

движение

Движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.

Все ли преобразования плоскости являются движением?

цели урока:

Рассмотреть геометрические преобразования пространства.

Ответить на вопрос: «Все ли преобразования пространства являются движением?».

Научиться строить фигуры используя геометрические преобразования.

Свойства движения

1) Прямые переходят в прямые.

2) Отрезок движением переводится в отрезок.

3) При движении луч переходит в луч .

4)Треугольник движением переводится в треугольник .

5) Движение сохраняет величины углов .

6)При движении сохраняются площади многоугольных фигур .

Симметрия относительно точки – центральная симметрия

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки О, называется центральной симметрией пространства относительно точки О. При этом точка О отображается на себя и называется центром симметрии.

Симметрия относительно прямой – осевая симметрия (определение точки, симметричной данной точке, относительно прямой m)

• Точка пространства, не лежащая на прямой m, называется симметричной точке М относительно прямой m, если отрезок перпендикулярен этой прямой и делится ею пополам.

Симметрия относительно прямой – осевая симметрия

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой m, называется осевой симметрией пространства относительно прямой m. Прямая m отображается на себя и называется осью симметрии.

Симметрия относительно плоскости – зеркальная симметрия

(определение точки, симметричной данной точке, относительно данной плоскости m)

Точка пространства, не лежащая на плоскости α, называется симметричной точке Х относительно плоскости α, если отрезок перпендикулярен этой плоскости и делится ею пополам.

Симметрия относительно плоскости – зеркальная симметрия

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется зеркальной симметрией пространства относительно плоскости α. Плоскость α отображается на себя и называется плоскостью симметрии. На иллюстрации горизонтальная плоскость – плоскость симметрии.

Параллельный перенос

Пусть дан вектор . Преобразование пространства, при котором каждая точка пространства М, отображается на такую точку что выполняется равенство =, называется параллельным переносом на вектор .

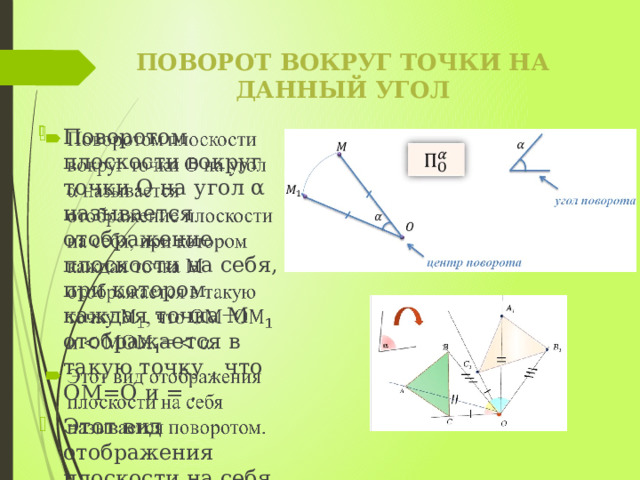
Поворот вокруг точки на данный угол

• Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку , что ОМ=О и = .
• Этот вид отображения плоскости на себя называется поворотом.

Движение. Виды движения.

Движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.

Виды движений:

1) Симметрия (центральная, осевая, зеркальная);

2) Параллельный перенос;

3) Поворот.

Закрепление изученного

• Сделайте в тетради такой же рисунок и постройте фигуру, симметричную данной относительно прямой l.

• Проверьте себя.

Закрепление изученного

• Сделайте в тетради такой же рисунок и постройте фигуру, симметричную данной относительно точки О.

• Проверьте себя.

Закрепление изученного

• Сделайте в тетради такой же рисунок и постройте фигуру, симметричную данной относительно прямой l.

• Проверьте себя.

Закрепление изученного

• Сделайте в тетради такой же рисунок и постройте фигуру, симметричную данной относительно прямой l.

• Проверьте себя.

Закрепление изученного

Закрепление изученного

Закрепление изученного

Домашнее задание

• Практическое задание (дизайн участка прямоугольной формы используя виды движений, изученных на уроке).
• Эксперимент.

Симметрия – идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство. В.Гейль