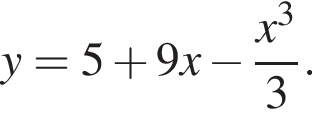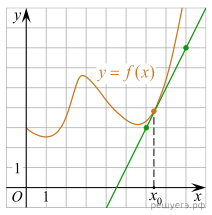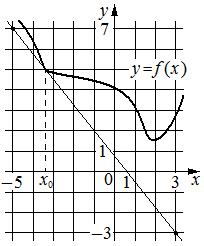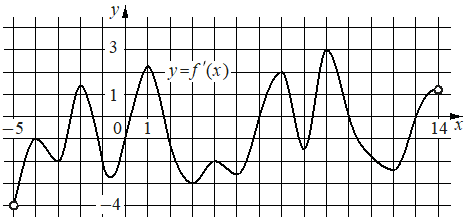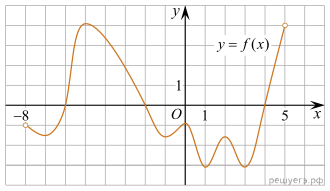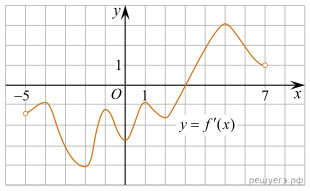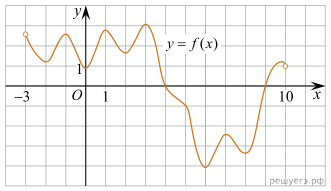Геометрический смысл производной. Применение производной к исследованию функций.

Геометрический смысл производной)

1. На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

1. На рисунке изображён график функции y  =  f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

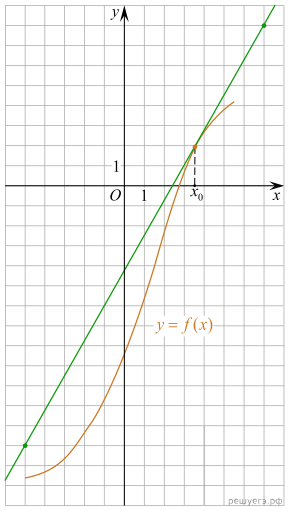
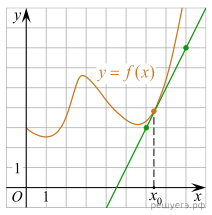
1. На рисунке изображены график функции y=f(x) и касательная к нему
   в точке с абсциссой x0. Найдите значение производной функции f(x) 
   в точке x0.

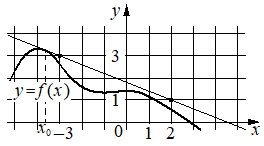
1. На рисунке изображены график функции y=f(x) и касательная к нему
   в точке с абсциссой x0. Найдите значение производной функции f(x) 
   в точке x0.

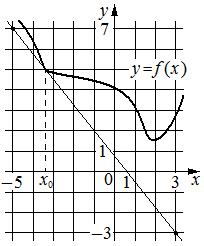
Применение производной к исследованию функций 1

1. На рисунке изображён график функции y=f(x). На оси абсцисс отмечено девять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9. Найдите количество отмеченных точек, в которых производная функции f(x) отрицательна.

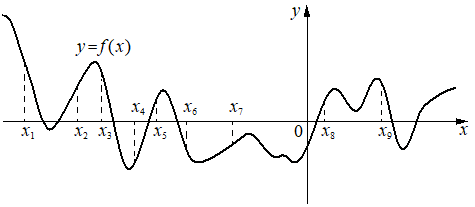
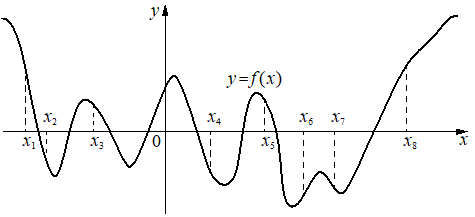
1. На рисунке изображён график функции y=f(x). На оси абсцисс отмечено восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Найдите количество отмеченных точек, в которых производная функции f(x) положительна.

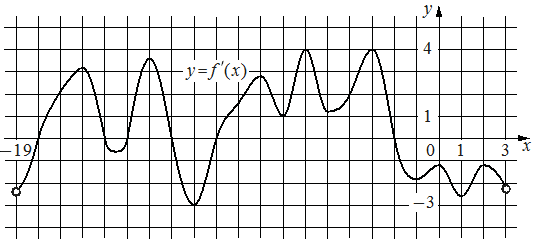
1. На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 19; 3). Найдите количество точек экстремума функции f(x), принадлежащих отрезку [− 17; − 4].

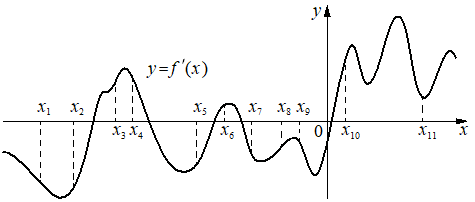
1. На рисунке изображён график y=f'(x) — производной функции f(x). 
   На оси абсцисс отмечено одиннадцать точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11. Сколько из этих точек принадлежит промежуткам убывания функции f(x)?

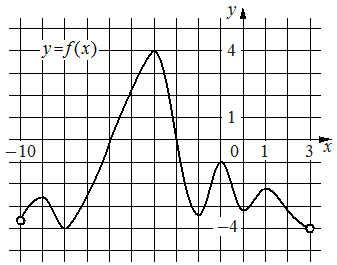
1. На рисунке изображён график функции y=f(x), определённой
   на интервале (− 10; 3). Найдите количество корней уравнения f'(x)=0, принадлежащих отрезку [− 7; 2].

1. На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 5; 14). Найдите количество точек минимума функции f(x), принадлежащих отрезку [− 4; 9].

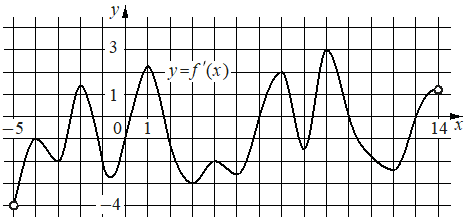
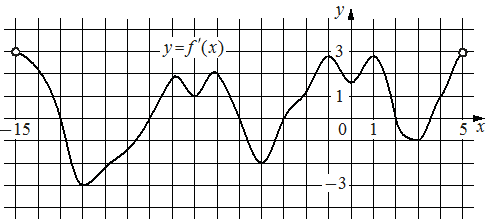
1. На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (− 15; 5). Найдите количество точек максимума функции f(x), принадлежащих отрезку [− 11; 4].

1. На рисунке изображён график y=f'(x) — производной функции f(x). 
   На оси абсцисс отмечено десять точек: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10. Сколько из этих точек принадлежит промежуткам возрастания функции f(x)?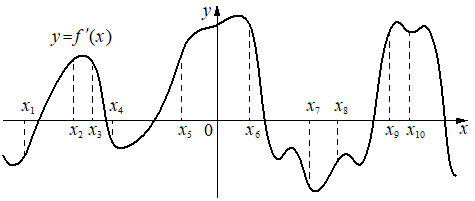

Применение производной к исследованию функций 2

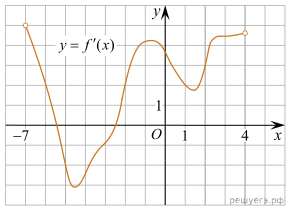
1.   На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

2. На рисунке изображен график функции 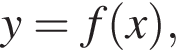определенной на интервале 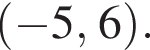Определите количество целых точек, в которых производная функции положительна.

3. На рисунке изображён график функции y  =  f(x), определённой на интервале (−8; 5). Найдите сумму точек экстремума функции f(x).

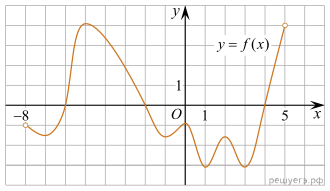
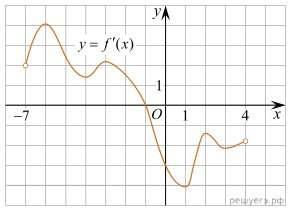
4. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). В какой точке отрезка [−6; −1] функция f(x) принимает наибольшее значение?

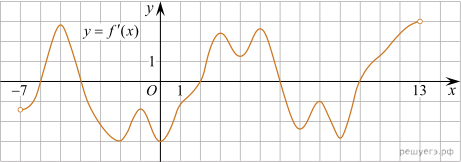
5.  На рисунке изображен график функции 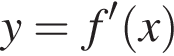  — определенной на интервале (−7; 13). Найдите количество точек максимума функции f(x) на отрезке [−5; 12].

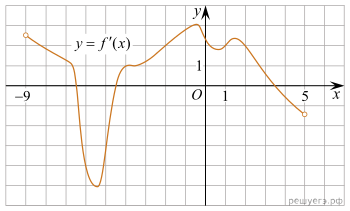
6. На рисунке изображён график функции 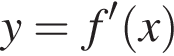  — производной функции 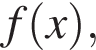определённой на интервале (−9;5). Найдите промежутки убывания функции 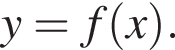В ответе укажите сумму целых точек, входящих в эти промежутки.

7. На рисунке изображён график функции 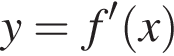  — производной функции 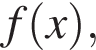определённой на интервале 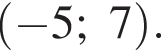Найдите точку экстремума функции 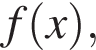принадлежащую отрезку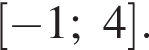

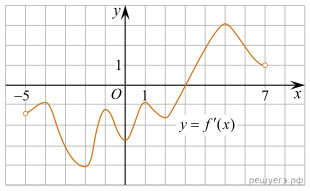
8. На рисунке изображён график функции y  =  f(x), определённой на интервале 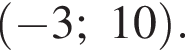Найдите количество точек, в которых производная функции f(x) равна 0.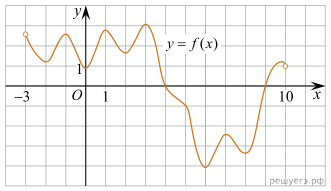

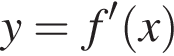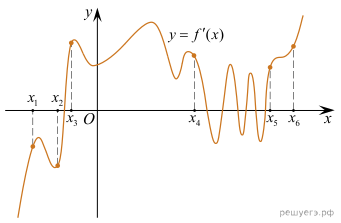
9.  На рисунке изображён график   — производной функции 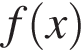и шесть точек на оси абсцисс: x₁, x₂, ..., x₆. В скольких из этих точек функция 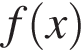возрастает?

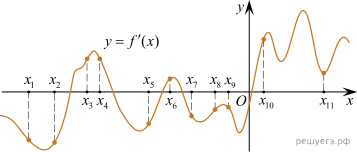
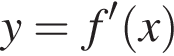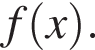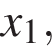
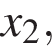
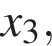
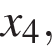
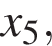
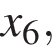
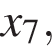
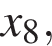
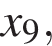
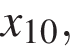
10.  На рисунке изображён график   — производной функции На оси абсцисс отмечено одиннадцать точек: 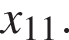Сколько из этих точек принадлежит промежуткам убывания функции

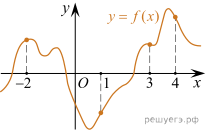
11. На рисунке изображен график функции и отмечены точки −2, 1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

12. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x₁, x₂, x₃, …, x₈. В скольких из этих точек производная функции f(x) положительна?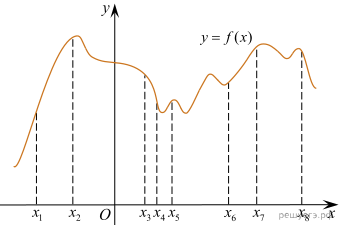

13. Найдите точку максимума функции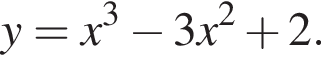

14. Найдите точку минимума функции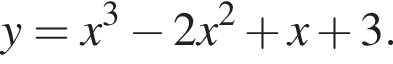

15. Найдите точку максимума функции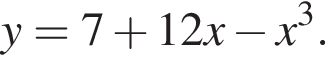

16. Найдите точку минимума функции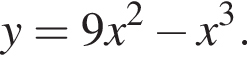

17. Найдите точку максимума функции