

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 29.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 27.05.2025 18:34

Хоцкая Наталья Васильевна
учитель математики
56 лет
Местоположение
Россия, г.Донецк
Геометрия, 9 класс Контрольная работа по теме «Длина окружности и площадь круга. Вычисление площадей».
Категория:
Геометрия
10.05.2025 17:57
© 2025, Хоцкая Наталья Васильевна 145 0



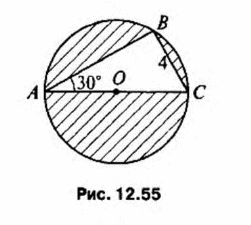
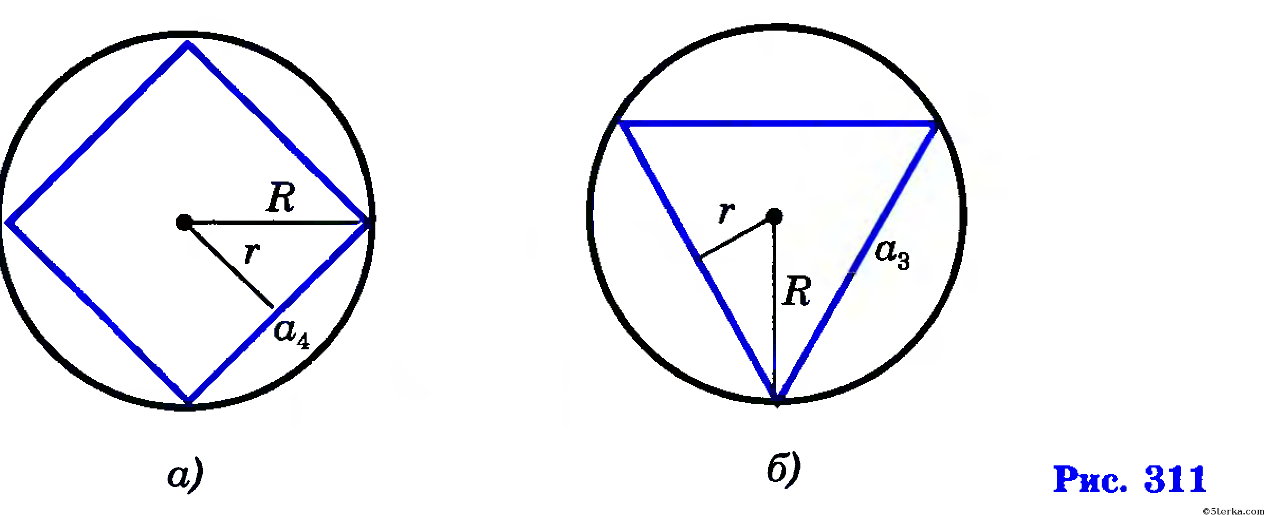
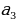 = 5√3 см; описана окружность
= 5√3 см; описана окружность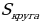 - ?
- ?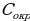 -?
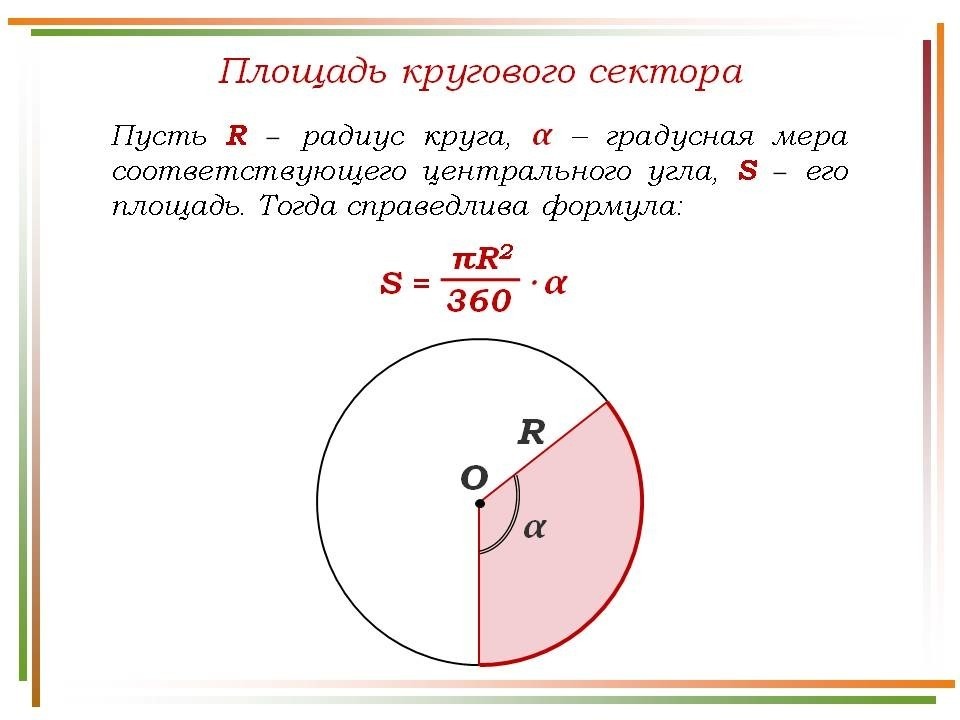
-?
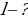
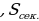 - ?
- ? 
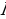 =
= 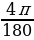 · 120° =
· 120° = 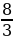 𝛑 = 2
𝛑 = 2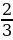 𝛑 (см)
𝛑 (см)
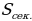 =
= 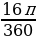 · 120° =
· 120° = 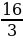 𝛑 = 5
𝛑 = 5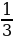 𝛑 (
𝛑 (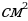 )
)
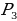 = 6√3 дм
= 6√3 дм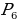 - ?
- ? 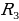 =
= 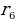 =
= 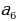 , выраженная через радиус вписанной окружности:
, выраженная через радиус вписанной окружности: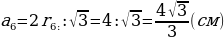
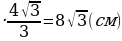
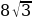 см.
см.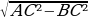 =
= 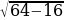 =
= 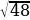 = 4
= 4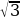 (см)
(см)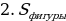 =
= 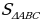 = 𝛑R² -
= 𝛑R² - 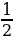 AB·BC = 16𝛑 - 8
AB·BC = 16𝛑 - 8 = 16𝛑 - 8
= 16𝛑 - 8

















