Геометрия 9 класс Открытый урок "Теорема косинусов"

Урок по теме «Теорема косинусов»

Сырцова Наталия Викторовна,

учитель математики

Урок по теме «Теорема косинусов»

Цели урока:

• образовательные – доказать теорему косинусов и показать её применение при решении задач; научить применять данную теорему при решении задач; выработать умение правильно выбрать теорему, по которой можно решить задачу.

• формировать математическую компетентность, углубляя и систематизируя теоретические знания, отрабатывая умения и навыки при решении упражнений, формировать социальные, поликультурные компетентности;

• развивающие – развитие логического мышления, алгоритмичности мышления, закрепление ранее изученного материала на практике решения задач, развитие навыков контроля, самоконтроля, взаимопомощи ; развивать сообразительность, творческое воображение, эстетические чувства, интерес к геометрии;

• воспитательные – воспитание умения внимательно слушать и оценивать устную информацию, воспитание умения четко формулировать свои мысли, воспитание коммуникативных способностей, аккуратности.

Тип урока: формирование новых знаний.

Ход урока:

1. Организационный момент

«Образование – это не количество прослушанных уроков, а количество понятых. Так что, если хотите идти вперед, то поспешайте медленно и будьте внимательны»

1. Проверка домашнего задания.

Актуализация знаний. Фронтальный опрос ранее изученного

Устная работа:

1. Мотивация урока.

1. Девиз нашего урока

«Наше оружие не пики,

Наше оружие не шашки,

Множество чёрных линий

Скрестим на белой бумаге.

Но ведь и в битве знаний

Тоже нужна отвага,

Боя не будет слышно,

Лишь зашуршит бумага».

1. Создание проблемной ситуации, которая подведет ребят к цели и задачам урока. В ходе беседы дети включаются в коллективную деятельность.

Задача:

П ри проектировании строительства железной дороги на некотором участке, возникла необходимость сооружения тоннеля, сквозь выступ горы между пунктами А и В. Для определения длины тоннеля выбрали на местности некоторый пункт С, из которого видны и доступны пункты А и В.

Ч ему равна длина тоннеля, если угол С равен 90⁰.

Ответ: АВ =

Как найти длину тоннеля, если угол С острый.

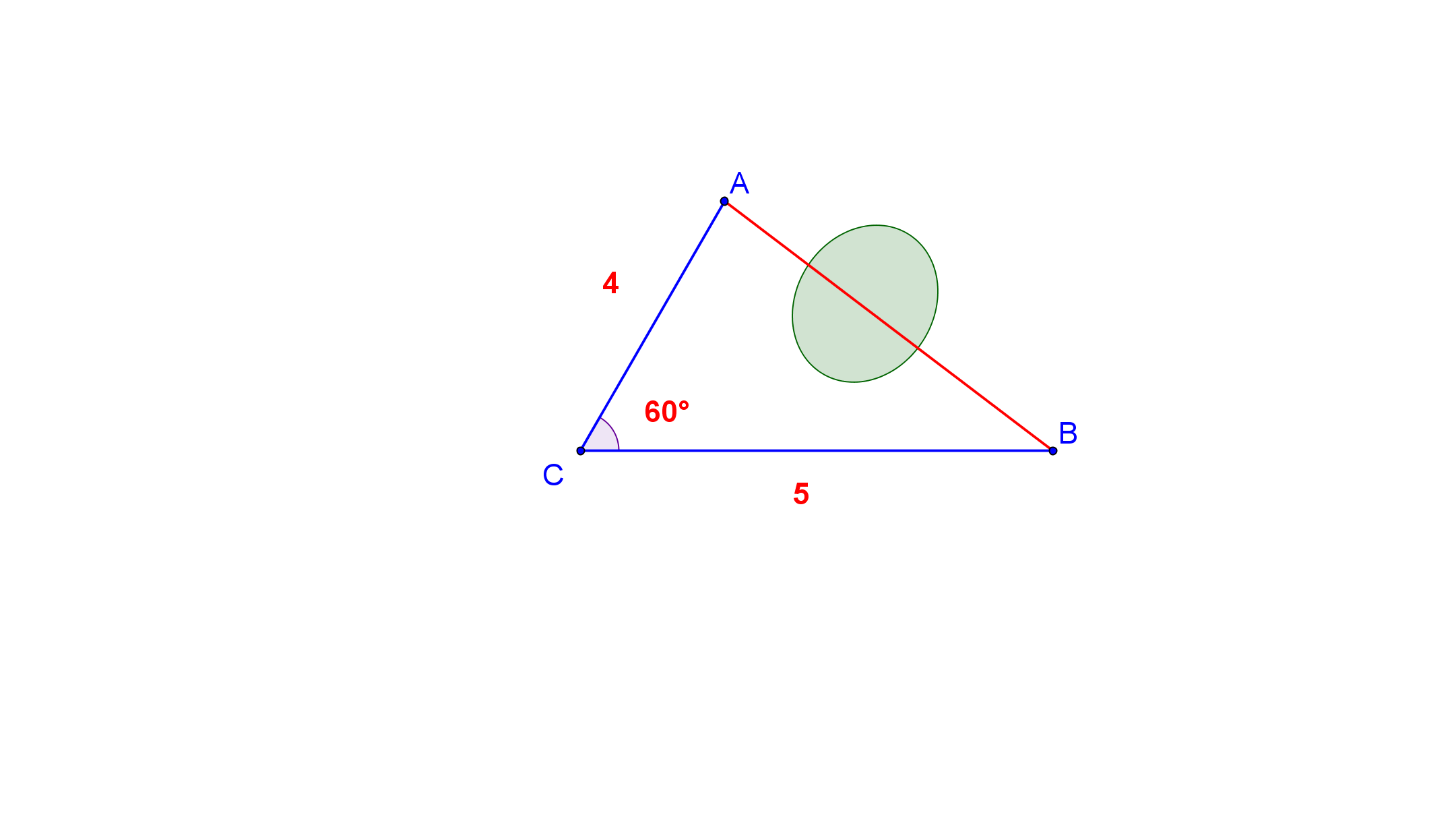Дано:

Р ешение:

• Проведем высоту АН.

• Из треугольника АНС находим

• А Н = АС Sinα

• А Н = 4 Sin 60⁰ =

• СН = АС Cosα.

• СН =

• ВН = 5-2=3.

• АВ =

А В =

1. Изучение нового материала.

От создания проблемной ситуации учащиеся плавно переходят к основной работе, по достижению поставленных целей.

На уроке осуществляется принцип наглядности. Доказательство теоремы, выступления учащихся оформлены и представлены на слайдах иллюстрациями к сообщениям учащихся в виде компьютерной презентации.

Из первого признака равенства треугольников следует, что две стороны и угол между ними однозначно определяют треугольник. А значит, по указанным элементам можно. Например. Найти третью сторону треугольника. Как это сделать. Показывает теорема косинусов.

Историческая справка: Впервые теорема косинусов была доказана учёным -математиком Аль-Бируни (973-1048 г.г.). С помощью данной теоремы и теоремы синусов которая будет доказана на последующих уроках, можно будет полностью решить поставленную в теме “Решение треугольников” задачу, т.е. вопрос о том, как зная одни из основных элементов треугольника (их 6: 3 угла и 3 стороны), найти другие.

Т еорема: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Доказательство:

Возможны три случая:

1. Угол А-острый;

2. угол А- тупой;

3. угол А –прямой.

Докажем первое равенство, два других доказываются аналогично.

(Первое равенство проговаривает и записывает учитель, а второе и третье кто-нибудь из учащихся.)

Иногда теорему косинусов называют обобщённой теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай, теорема Пифагора. В самом деле, если в треугольнике АВС угол А прямой, то соs А = соs 90° = 0 и по формуле получаем , то есть квадрат гипотенузы равен сумме квадратов катетов.

Физкультминутка.

1. Первичное осмысление и применение изученного материала.

На этапе первичного закрепления дети работают коллективно, под руководством учителя. На следующем этапе закрепления ребята работают в группах, что позволяет им чувствовать себя полноценным участником образовательного процесса.

Задачи по готовым чертежам. При решении задач учащиеся каждый раз проговаривают формулировку теоремы.

Задача №1

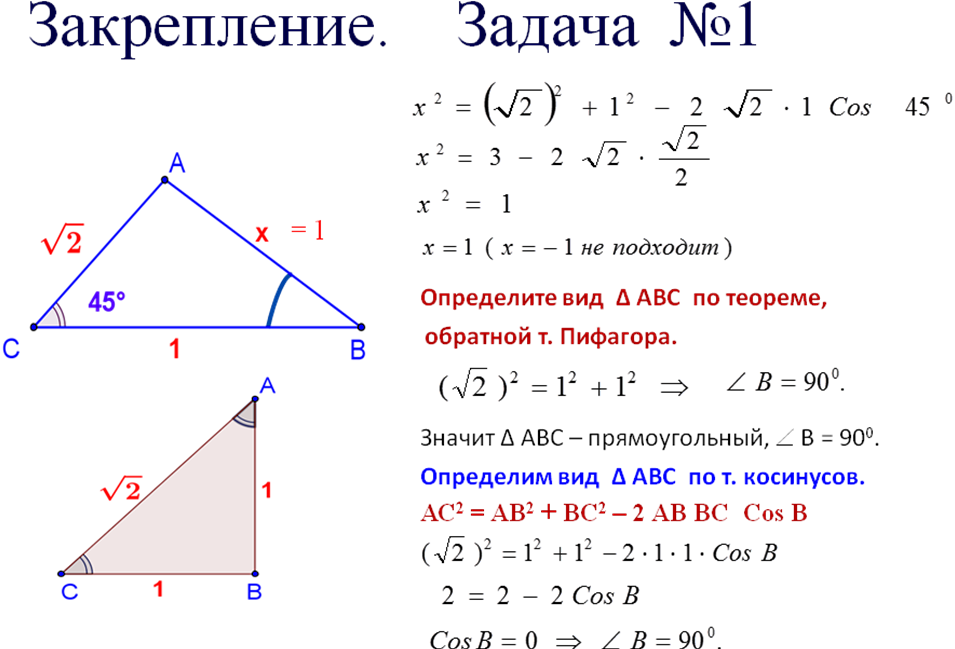
Задача №2

Задача № 3(работа в группах)

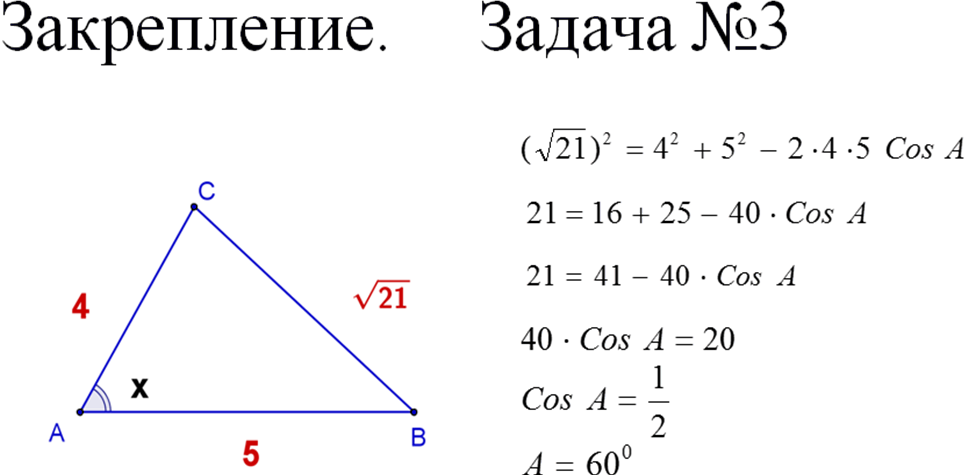
Задача № 4

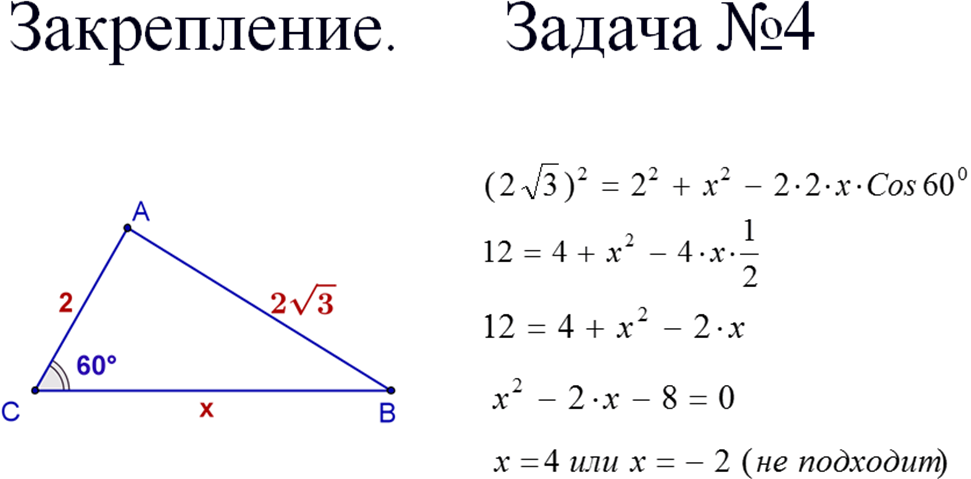
Ещё раз повторить, как звучит теорема косинусов.

1. Подведение итогов. Заслушиваются оценки учащихся.

Проводится тест

1. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то эта сторона лежит против:

а) тупого угла
б) прямого угла
в) острого угла

1. В  АВС известны длины сторон АВ и ВС. Чтобы найти сторону АС, необходимо знать величину:

а) угла А
б) угла В
в) угла С

1. Если в  АВС   А=48°;   В=72°, то наибольшей стороной треугольника является сторона:

а) АВ
б) АС
в) ВС

Высвечиваются правильные ответы на экране, учащиеся сами проверяют свои ответы и оценивают себя.

1. Рефлексия.

1.Какой способ доказательства наиболее вам понравился и почему?

2.Выучить тот способ, который наиболее доступен.

1. Задание на дом.

Выучить §6, доказательство теоремы косинусов.

Решить задания : с. 257, № 1025 (ж, е); № 1028, 1031 (б)

Сообщение «Из истории открытия теоремы косинусов».

7