Геометрия 9-з класс презентация "Симметрия относительно прямой"

Павлоградська ЗШ № 9

Симетрія відносно прямої

Геометрія, 9 клас

Суріна Н.О.

Притча про осьову симетрію

Якось чужоземець, вражений красою Бухарського мінарету Кальян, вигукнув: “Як ви будуєте такі високі мінарети?” – “Дуже просто”, - відповів Ходжа

Насреддін. І, хизуючись своєю дотепністю, пояснив:

Спочатку викопуємо

глибокий колодязь,

а потім вивертаємо

його навиворіт

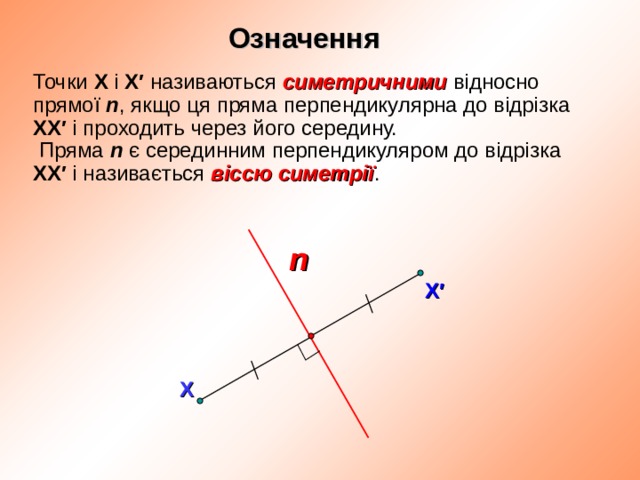
Означення

Точки Х і Х′ називаються симетричними відносно прямої n , якщо ця пряма перпендикулярна до відрізка ХХ′ і проходить через його середину.

Пряма n є серединним перпендикуляром до відрізка ХХ′ і називається віссю симетрії .

n

Х′

Х

3

Усні вправи

• Назвіть точки, симетричні відносно прямої g .

• Чому точки А і В, D і Е, F і К не є симетричними відносно прямої g .
• Покажіть точку, симетричну точці О відносно прямої g .

Побудувати відрізок А 1 В 1 симетричний відрізку АВ відносно прямої

n

n

Пряма – вісь симетрії

В

В 1

А 1

А

n

А→А 1 , В → В 1, АВ → А 1 В 1

5

Симетричні фігури

• Перетворенням симетрії (симетрією) відносно прямої a називають таке перетворення фігури F у фігуру F ′, внаслідок якого кожна точка Х фігури F переходить у точку Х′ фігури F ′, симетричну точці Х відносно прямої a .

Фігури F і F ′ називають симетричними відносно прямої a .

F

F ′

Симетрію відносно прямої називають осьовою симетрією .

X

X ′

O

a

Побудувати трикутник А 1 В 1 С 1 симетричний трикутнику АВС відносно прямої а

А

А 1

С 1

С

В 1

В

a

Пряма а – вісь симетрії

А→А 1 , С →С 1 , В→В 1,

∆ АВС→∆А 1 В 1 С 1

Побудувати трикутник А 1 В 1 С 1 симетричний трикутнику АВС відносно прямої a

А

В

a

Пряма –

вісь симетрії

С

А→А,

С →С,

В→В 1,

∆ АВС→∆АВ 1 С

a

В 1

Якщо перетворення симетрії відносно прямої n переводить фігуру F у себе, то така фігура називається симетричною відносно прямої n ,

а сама пряма n – віссю симетрії фігури F .

n

А

В

D

С

8

Усні вправи

• Чи можна фігури, зображені на малюнках назвати симетричними відносно певної осі?
• Назвіть номери фігур, що мають одну, дві, три, чотири, безліч осей симетрії.
• Скільки осей симетрії мають прямокутник і ромб?

Основна властивість осьової симетрії

y

Y(x 2 ;y 2 )

Теорема

Осьова симетрія є переміщенням.

Y′(-x 2 ;y 2 )

Доведення.

Осьова симетрія відносно прямої n : точка Х – переходить в точку Х ′ , точка Y переходить у точку Y ′.

n =Оу.

Тоді: Х (х 1 ;у 1 )→Х ′ (-х 1 ;у 1 ), Y (х 2 ;у 2 )→ Y ′ (-х 2 ;у 2 ).

Х (x 1 ;y 1 )

Х ′(-x 1 ;y 1 )

O

x

Відстань між точками:

Х Y =

Х ′ Y ′ =

Отже, Х Y = Х ′ Y ′.

Властивості осьової симетрії:

1) Перетворення осьової симетрії є переміщенням.

2) Осьова симетрія перетворює пряму на пряму; відрізок – на відрізок; многокутник – на рівний йому многокутник.

3)Точки, що належать осі симетрії, відображаються самі на себе.

4)Якщо точки М(х;у) і N (х 1 ; у 1 ) симетричні відносно:

А) осі Ох, то виконується умова: х 1 =х, у 1 =-у;

Б) осі Оу, то виконується умова х 1 =-х, у 1 =у.

Перевір себе

• Які точки називаються симетричними відносно прямої?
• Яке перетворення називається симетрією відносно даної прямої?
• Яка фігура називається симетричною відносно даної прямої?
• Що таке вісь симетрії? Наведіть приклади.

Побудувати фігуру, симетричну даній відносно прямої n .

n