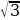| ПРИМЕР 7. Построить треугольник по трем высотам.[4] ДОКАЗАТЕЛЬСТВО. Задачу надо понимать так: даны три отрезка 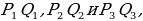 требуется с помощью циркуля и линейки построить треугольник требуется с помощью циркуля и линейки построить треугольник 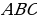 , высоты которого проведенные из вершин , высоты которого проведенные из вершин 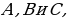 соответственно равны соответственно равны 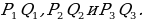  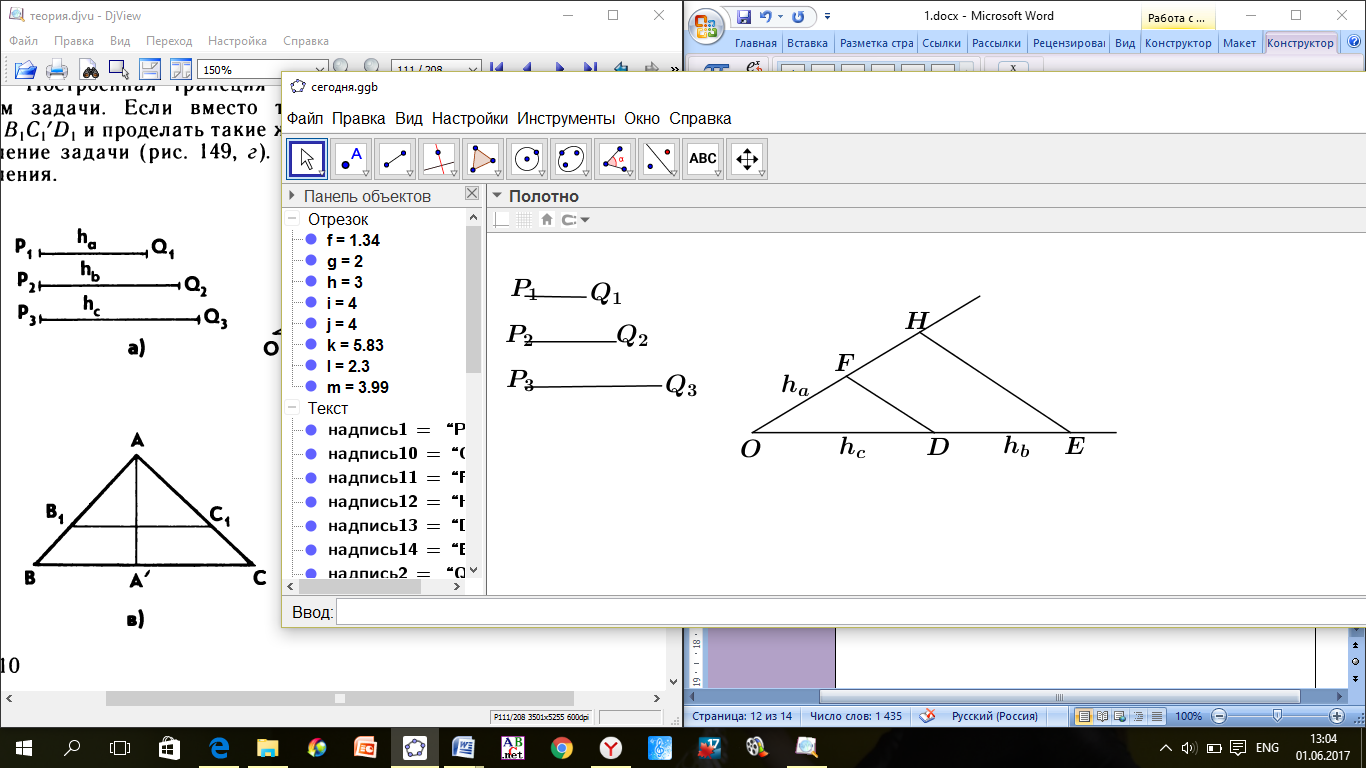 АНАЛИЗ ЗАДАЧИ. Обозначим через АНАЛИЗ ЗАДАЧИ. Обозначим через 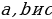 длины сторон искомого треугольника, противолежащих углам длины сторон искомого треугольника, противолежащих углам 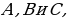 а через а через 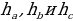 длины отрезков длины отрезков 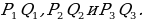 Воспользуемся равенствами Воспользуемся равенствами 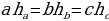 (каждое из произведений равно удвоенной площади треугольника). Из первого равенства получаем пропорцию (каждое из произведений равно удвоенной площади треугольника). Из первого равенства получаем пропорцию 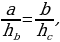 а из второго равенства имеем а из второго равенства имеем 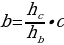 и поэтому и поэтому
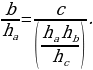
Таким образом, 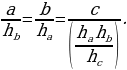
Полученные равенства показывают, что искомый треугольник со сторонами  подобен треугольнику со сторонами подобен треугольнику со сторонами 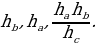 Это дает ключ к решению задачи. ПОСТРОЕНИЕ. По данным отрезкам  с длинами с длинами 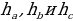 построим отрезок, длина которого равна построим отрезок, длина которого равна 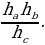 Это можно сделать следующим образом: построим какой-нибудь угол и отложим от его вершины Это можно сделать следующим образом: построим какой-нибудь угол и отложим от его вершины  на одной стороне угла последовательно отрезки на одной стороне угла последовательно отрезки  и и 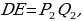 а на другой стороне угла отрезок а на другой стороне угла отрезок 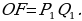  Проведем прямую Проведем прямую 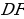 , а затем через точку , а затем через точку 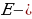 прямую, параллельную прямую, параллельную 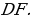 Она пересекает луч Она пересекает луч 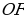 в точке в точке 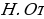 резок резок 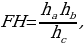 что следует из пропорции что следует из пропорции 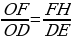 . .
Далее построим треугольник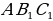 по трем сторонам по трем сторонам 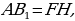 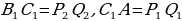 . Этот треугольник, как уже было отмечено, подобен искомому треугольник у. через вершину . Этот треугольник, как уже было отмечено, подобен искомому треугольник у. через вершину  проведем высоту треугольника проведем высоту треугольника 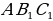 и отложим на ней (или на ее продолжении) отрезок и отложим на ней (или на ее продолжении) отрезок  , равный , равный 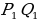 . Через точку . Через точку 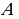 проведем прямую, параллельную проведем прямую, параллельную 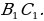 Точки Точки 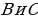 пересечения этой прямой с лучами пересечения этой прямой с лучами 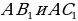 являются вершинами искомого треугольника являются вершинами искомого треугольника 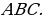
ДОКАЗАТЕЛЬСТВО. Построенный треугольник 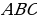 подобен треугольнику подобен треугольнику 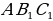 и, следовательно, подобен искомому треугольнику. Высота, проведенная из вершины и, следовательно, подобен искомому треугольнику. Высота, проведенная из вершины 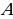 в построенном треугольнике в построенном треугольнике 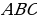 , равна , равна  , как должно быть в искомом треугольнике, т.е. сходственные высоты в треугольнике , как должно быть в искомом треугольнике, т.е. сходственные высоты в треугольнике 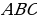 и искомом треугольнике равны. Значит, коэффициент подобия равен 1, а это и означает, что треугольник и искомом треугольнике равны. Значит, коэффициент подобия равен 1, а это и означает, что треугольник 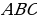 есть искомый. есть искомый. ИССЛЕДОВАНИЕ. Искомый треугольник 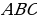 можно построить в том случае, если можно построить треугольник можно построить в том случае, если можно построить треугольник 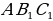 , стороны которого равны соответственно , стороны которого равны соответственно 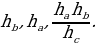 Следовательно, данные отрезки Следовательно, данные отрезки 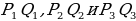 должны быть такими, чтобы из отрезков с длинами должны быть такими, чтобы из отрезков с длинами 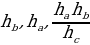 можно было построить треугольник. В таком случае задача имеет решение. можно было построить треугольник. В таком случае задача имеет решение. ПРИМЕР 8. Постройте равнобедренный треугольник, если даны прямая, на которой лежит медиана, проведенная из вершины, две точки на боковых сторонах и точка на основании. РЕШЕНИЕ. 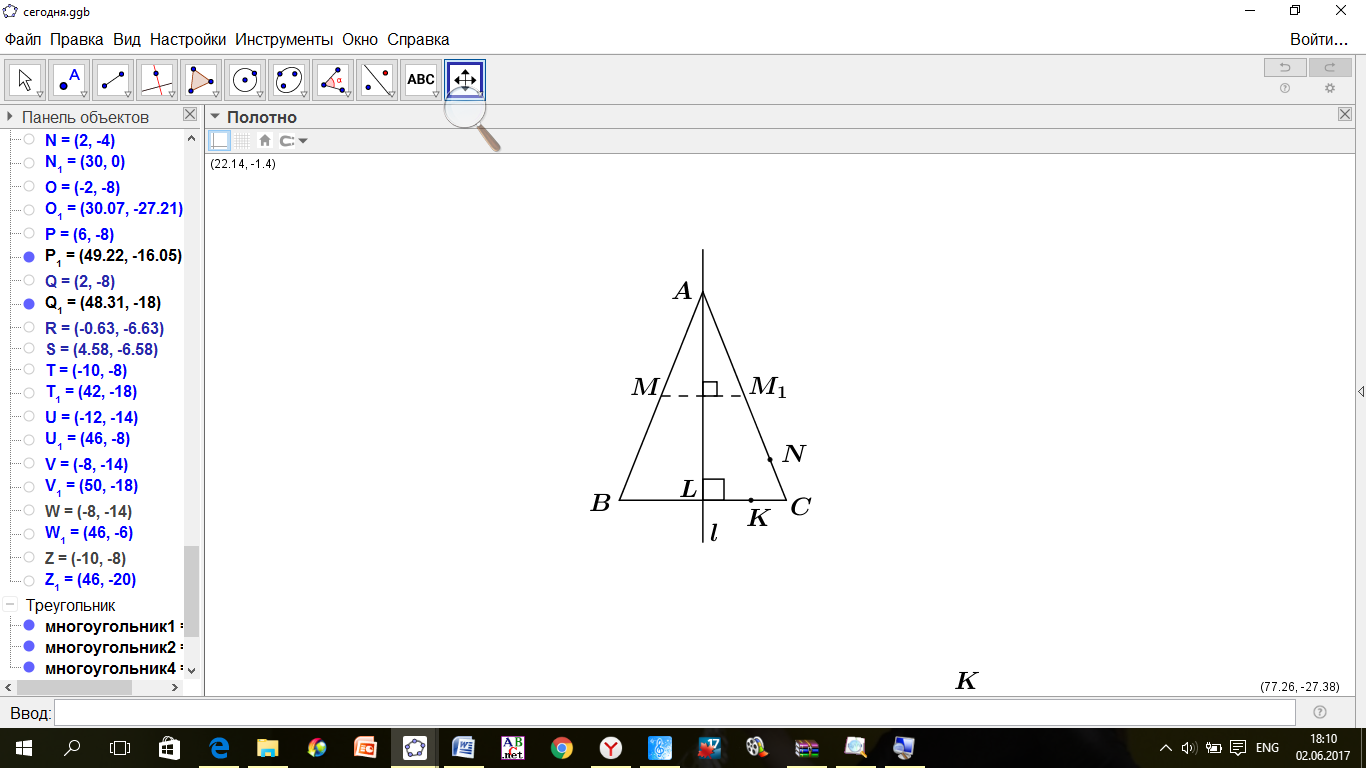 АНАЛИЗ ЗАДАЧИ. Предположим, что искомый равнобедренный треугольник АНАЛИЗ ЗАДАЧИ. Предположим, что искомый равнобедренный треугольник  построен. Данные точки построен. Данные точки  лежат на боковых сторонах лежат на боковых сторонах 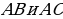 соответственно, данная точка соответственно, данная точка 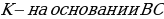 , медиана , медиана 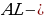 на данной прямой на данной прямой 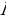 . Поскольку медиана . Поскольку медиана 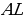 равнобедренного равнобедренного  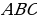 является также его биссектрисой, а биссектриса есть ось симметрии угла, то точка является также его биссектрисой, а биссектриса есть ось симметрии угла, то точка 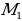 , симметричная точке , симметричная точке 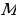 относительно прямой относительно прямой 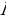 , лежит на боковой стороне , лежит на боковой стороне 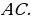 В то же время, медиана В то же время, медиана 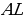 является также высотой равнобедренного треугольника является также высотой равнобедренного треугольника 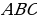 . Поэтому точка . Поэтому точка 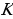 лежит на прямой, перпендикулярной данной прямой лежит на прямой, перпендикулярной данной прямой 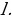
ПОСТРОЕНИЕ. Отсюда вытекает следующее построение. Строим точку 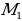 , симметричную данной точке , симметричную данной точке 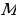 относительно данной прямой относительно данной прямой 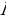 . . ДОКАЗАТЕЛЬСТВО. Если точка 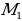 отлична от данной точки отлична от данной точки 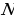 и прямая и прямая 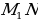 пересекает данную прямую пересекает данную прямую 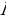 , задача имеет единственное решение. В этом случае прямая , задача имеет единственное решение. В этом случае прямая 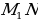 содержит одну из боковых сторон искомого треугольника, а прямая, симметричная ей относительно данной прямой содержит одну из боковых сторон искомого треугольника, а прямая, симметричная ей относительно данной прямой 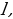 — вторую. Основание искомого треугольника получим, проведя через данную точку — вторую. Основание искомого треугольника получим, проведя через данную точку 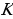 прямую, перпендикулярную прямой прямую, перпендикулярную прямой 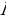 . . ИССЛЕДОВАНИЕ. Если прямая 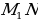 параллельна параллельна 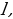 то задача не имеет решений. Если же точка то задача не имеет решений. Если же точка  совпадет с совпадет с  , задача имеет бесконечно много решений. , задача имеет бесконечно много решений.
| 








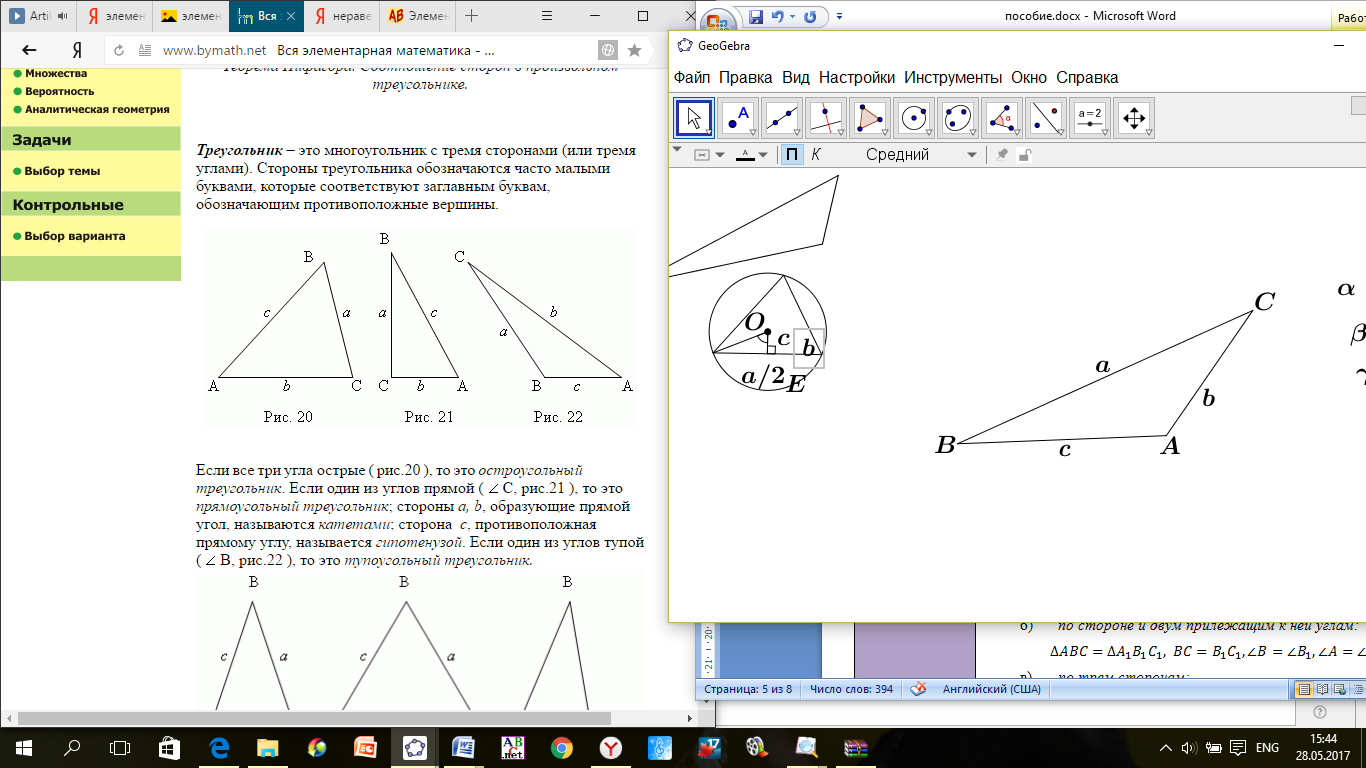
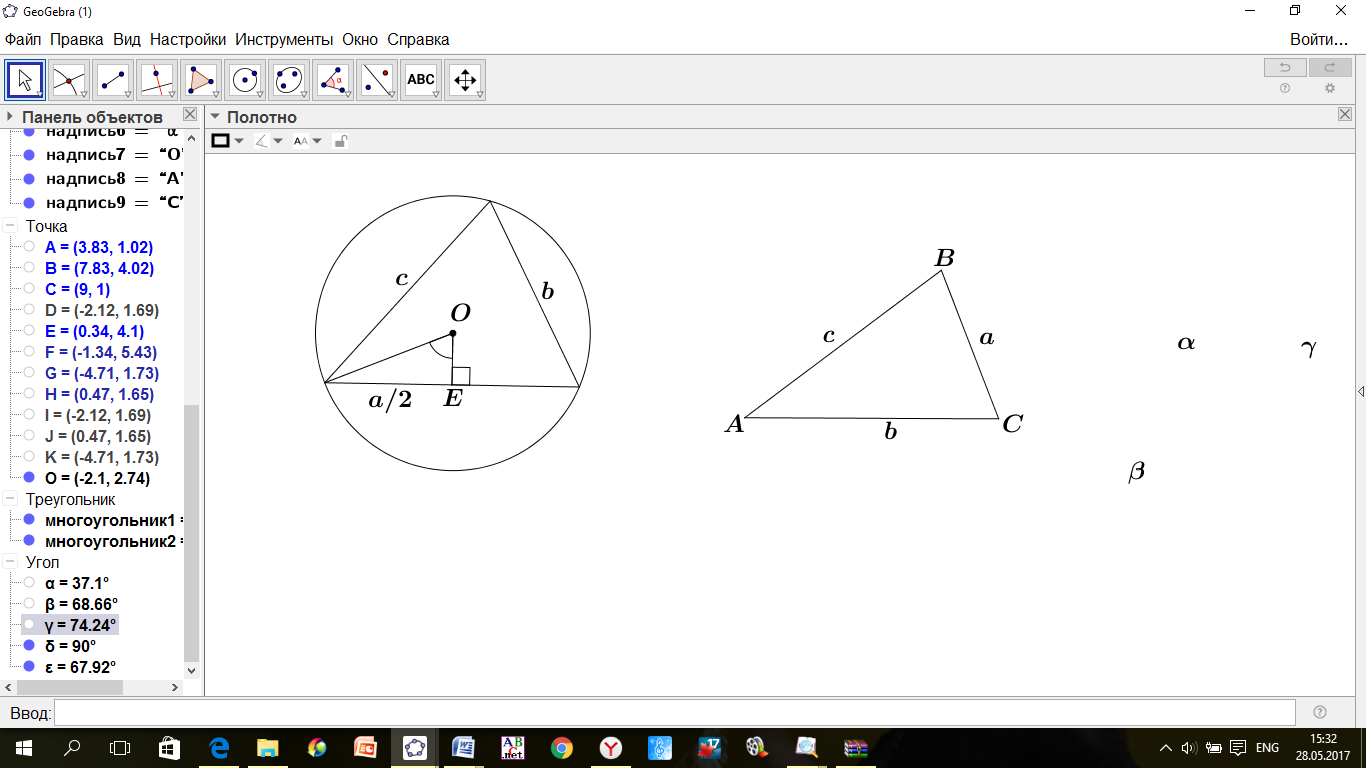 В случае если один из углов треугольника прямой, то это прямоугольный треугольник.
В случае если один из углов треугольника прямой, то это прямоугольный треугольник.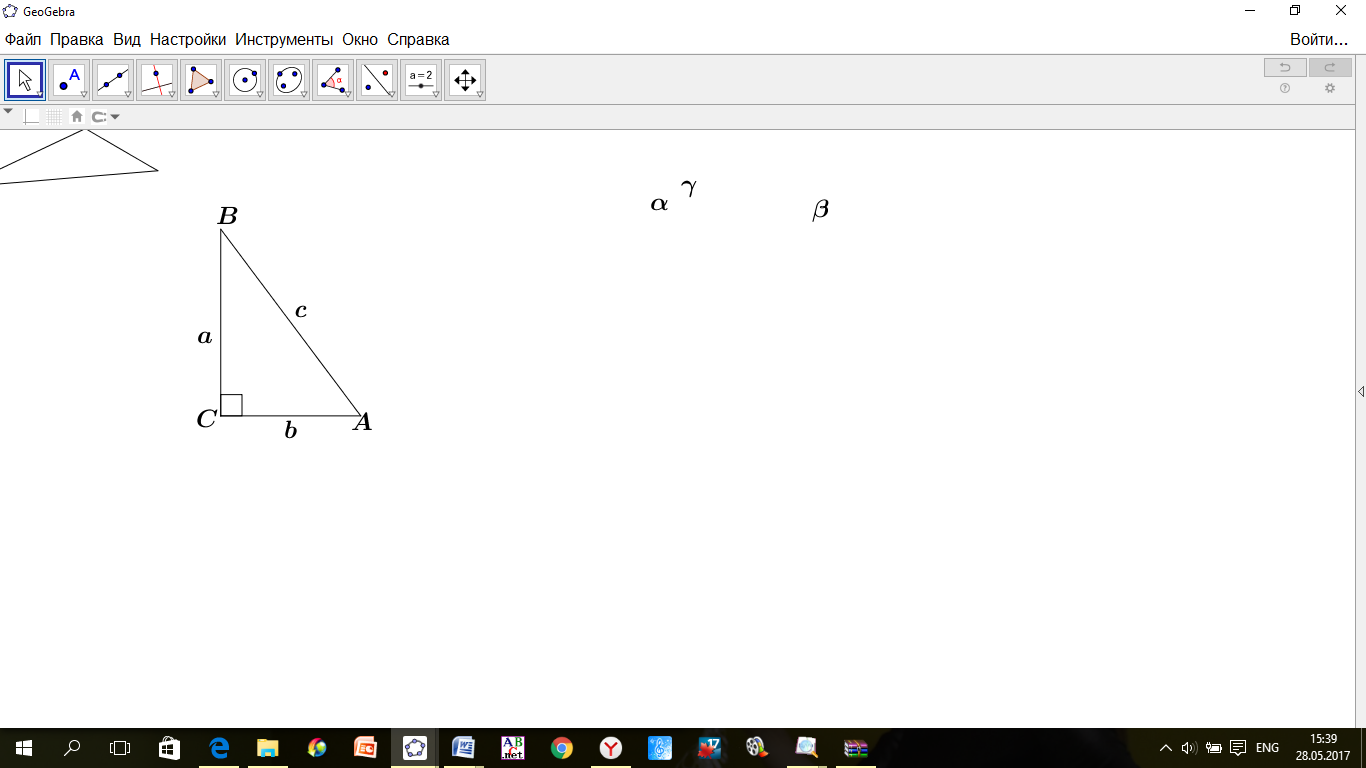
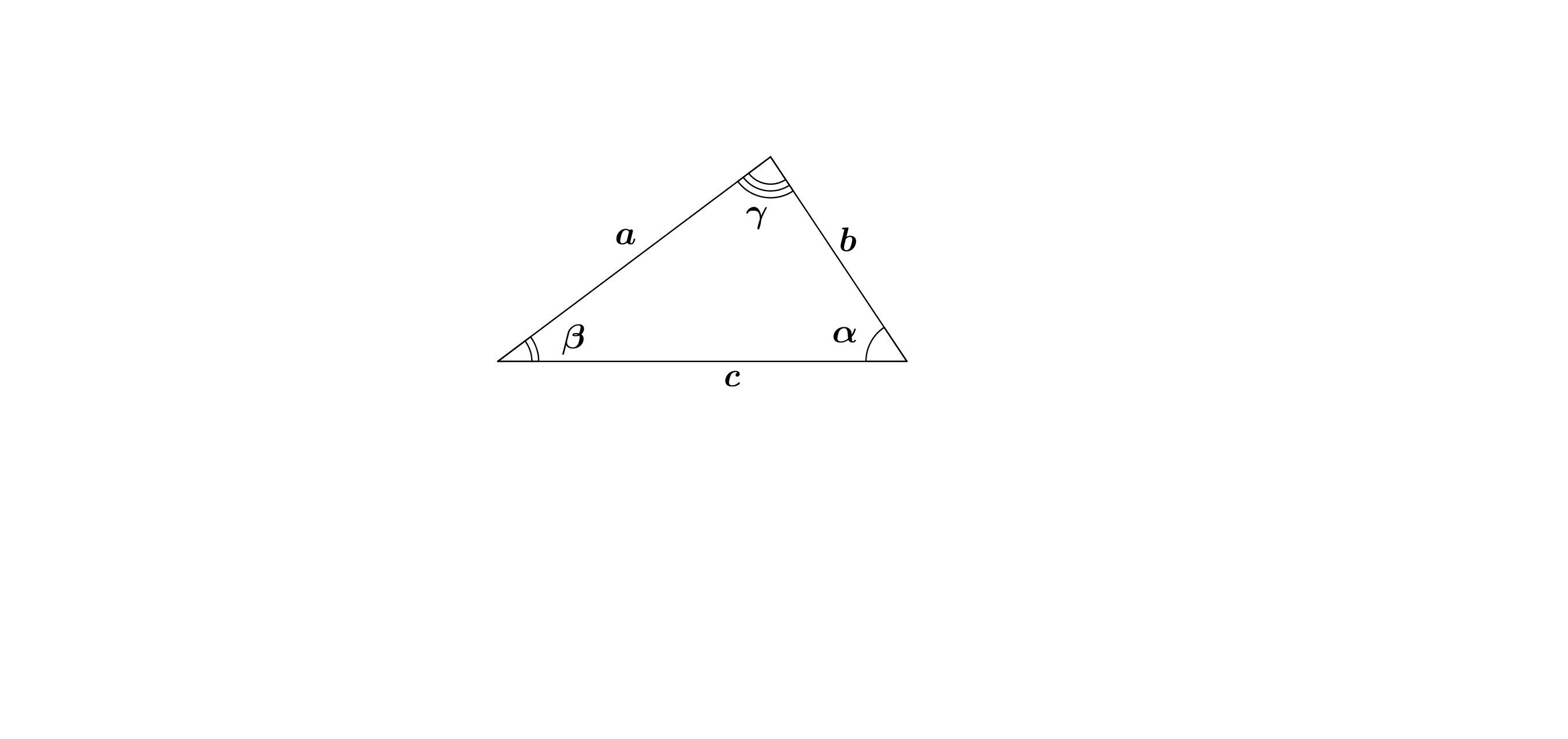
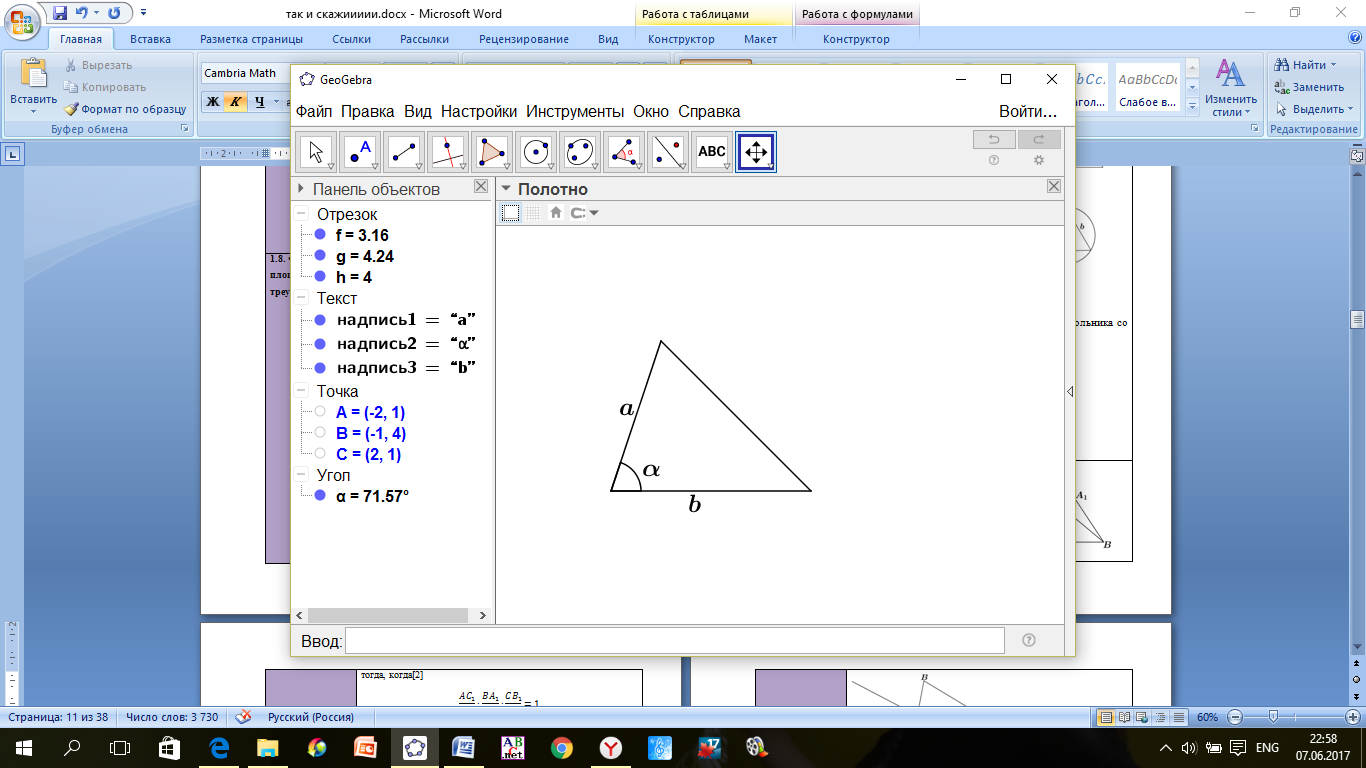
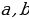 и
и  - стороны треугольника, при этом
- стороны треугольника, при этом 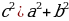 , то треугольник остроугольный;
, то треугольник остроугольный;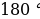 .
.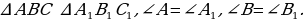
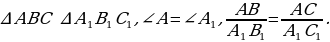
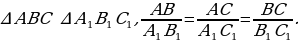
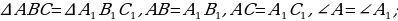
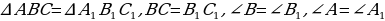 ;
;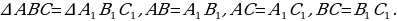
 , которая делит каждую из них в отношении 2:1, считая от вершины треугольника.
, которая делит каждую из них в отношении 2:1, считая от вершины треугольника. 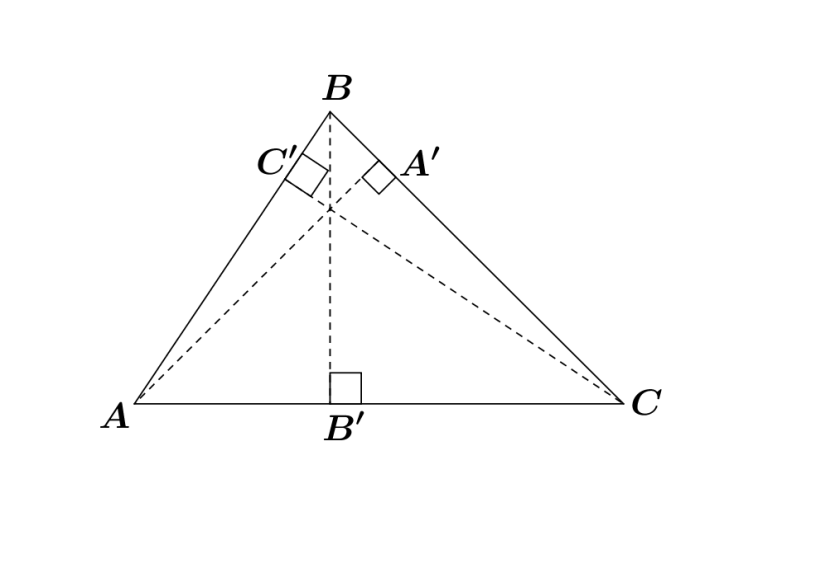
 Теорема 1. Свойство медианы в прямоугольном треугольнике:
Теорема 1. Свойство медианы в прямоугольном треугольнике: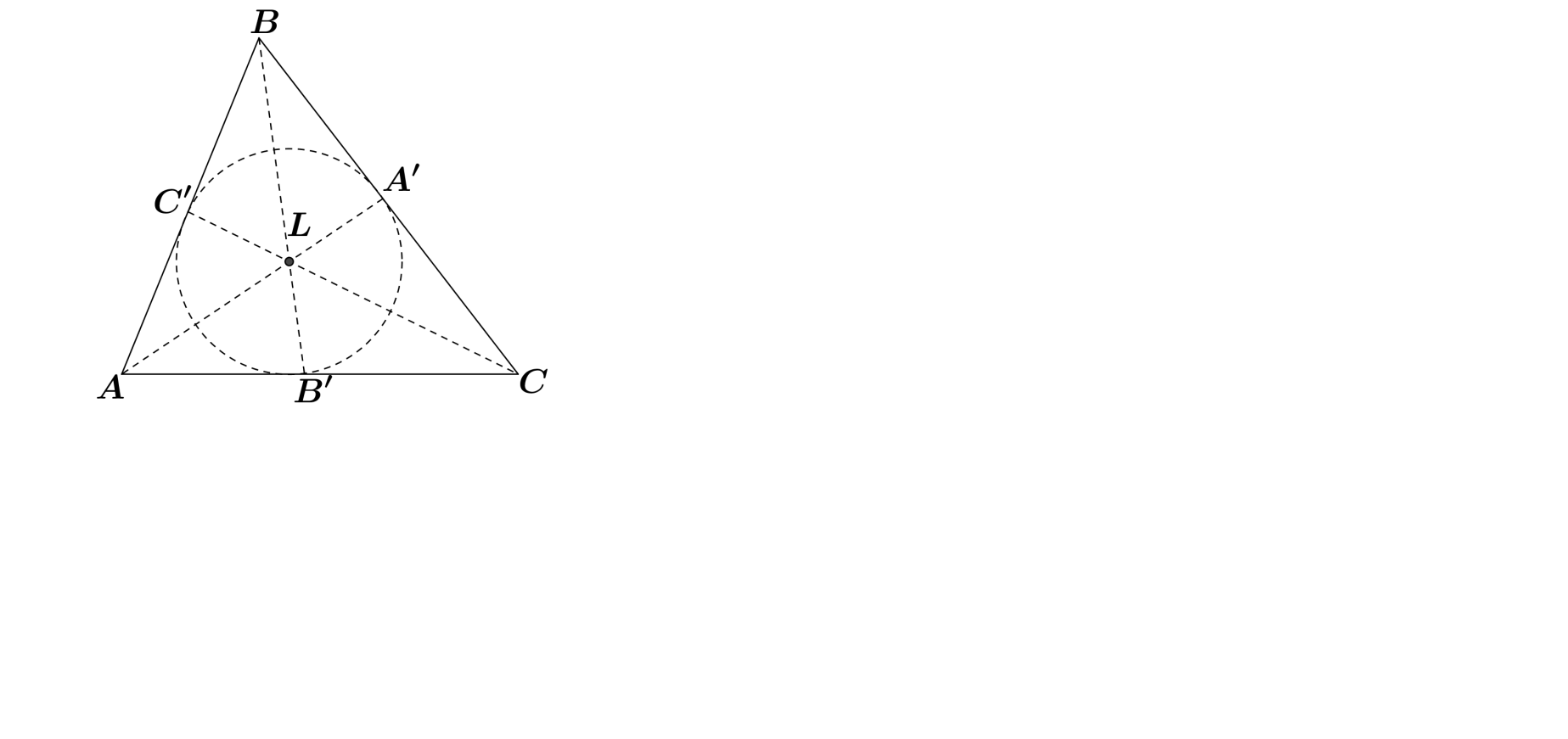 Центр вписанной в треугольник окружности. Биссектрисы треугольника пересекаются в одной точке
Центр вписанной в треугольник окружности. Биссектрисы треугольника пересекаются в одной точке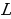 , которая равноудалена от трех сторон треугольника и потому является центром вписанной в треугольник окружности.
, которая равноудалена от трех сторон треугольника и потому является центром вписанной в треугольник окружности.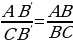
 пересекаются в одной точке О, являющейся центром описанного круга (точки
пересекаются в одной точке О, являющейся центром описанного круга (точки  – середины сторон треугольника
– середины сторон треугольника 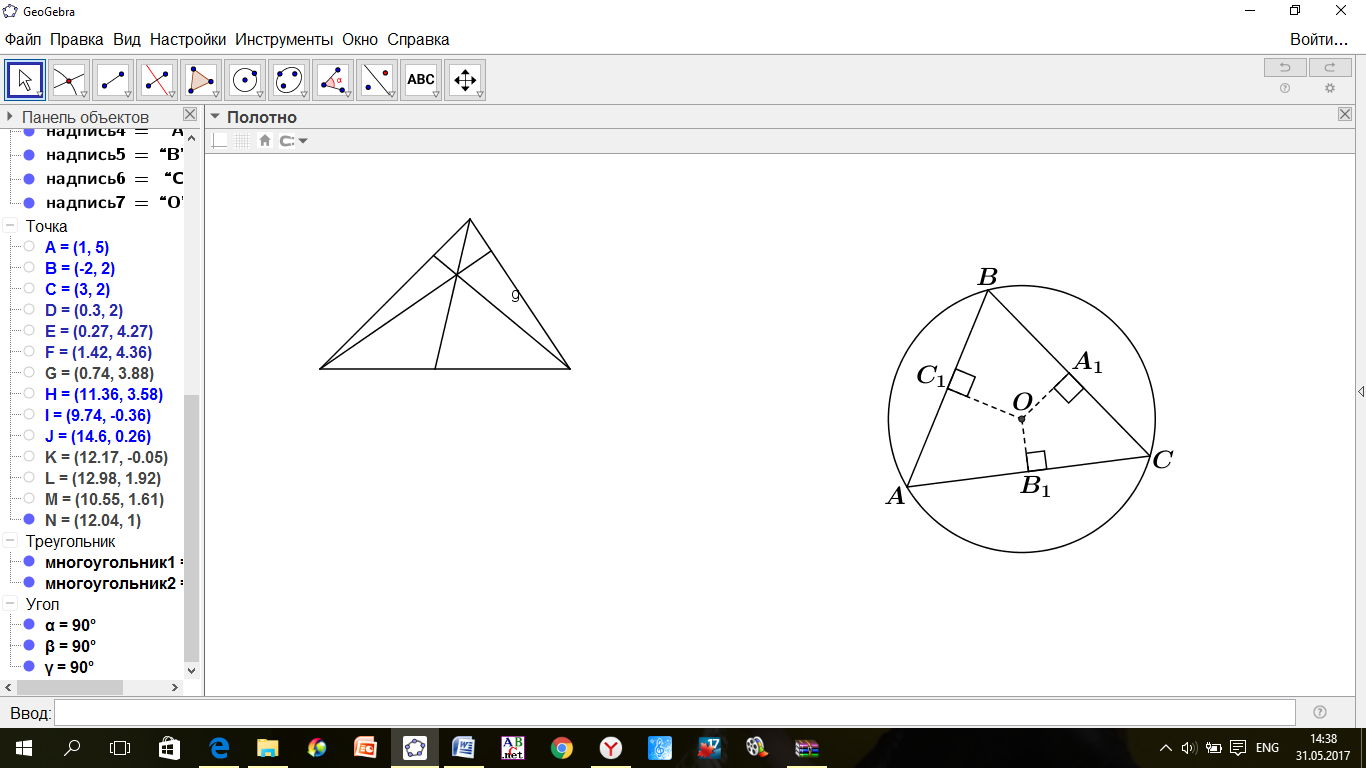
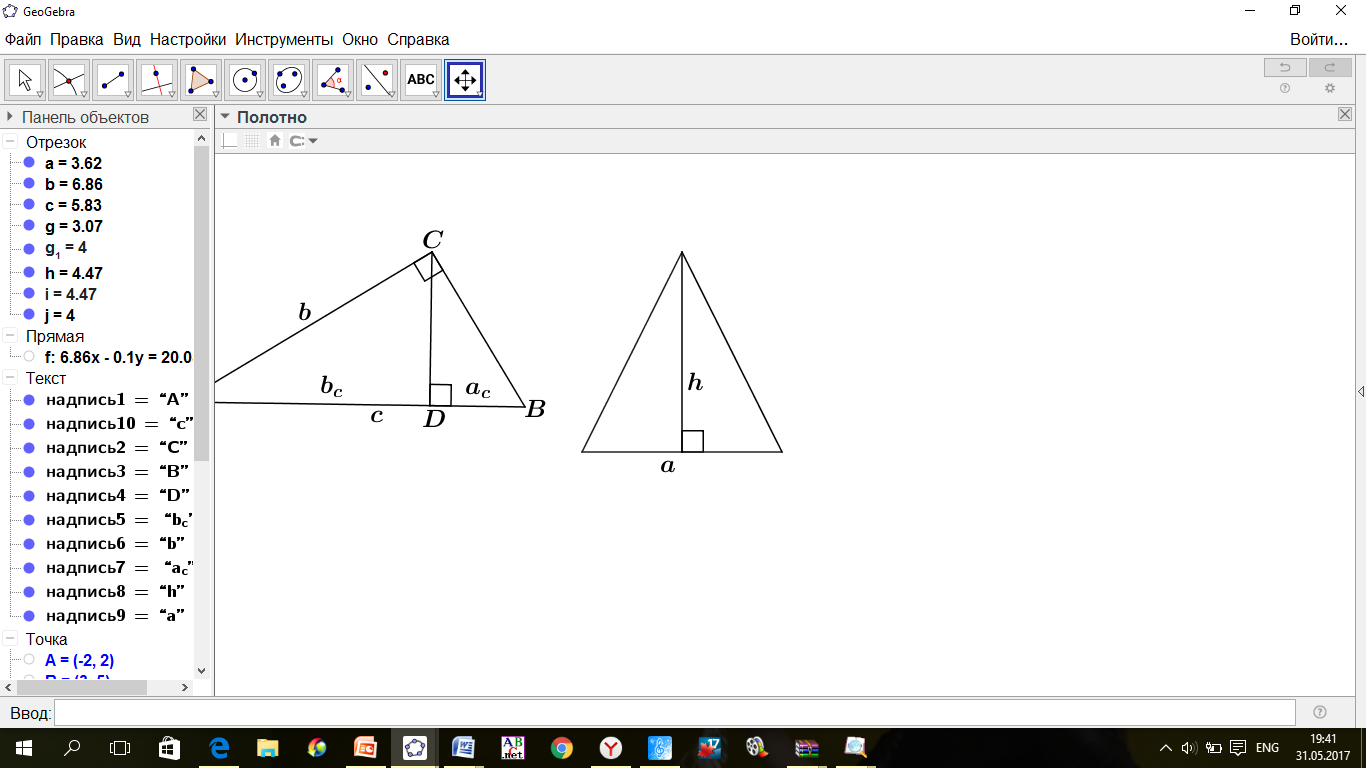
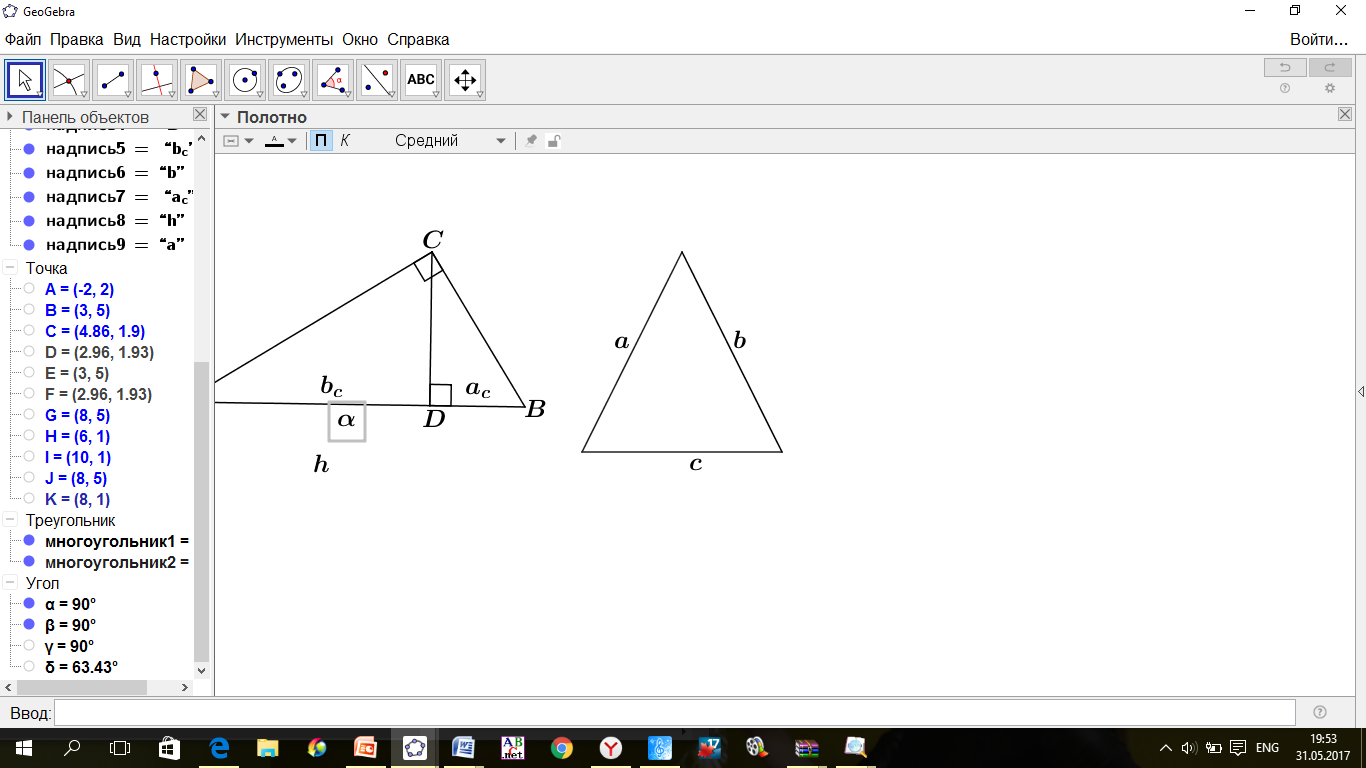
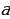 и
и 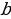 – катеты,
– катеты, 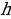 - высота,
- высота, 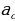 и
и 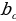 - проекции катетов на гипотенузу, то:
- проекции катетов на гипотенузу, то: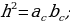
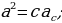
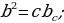
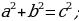
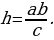
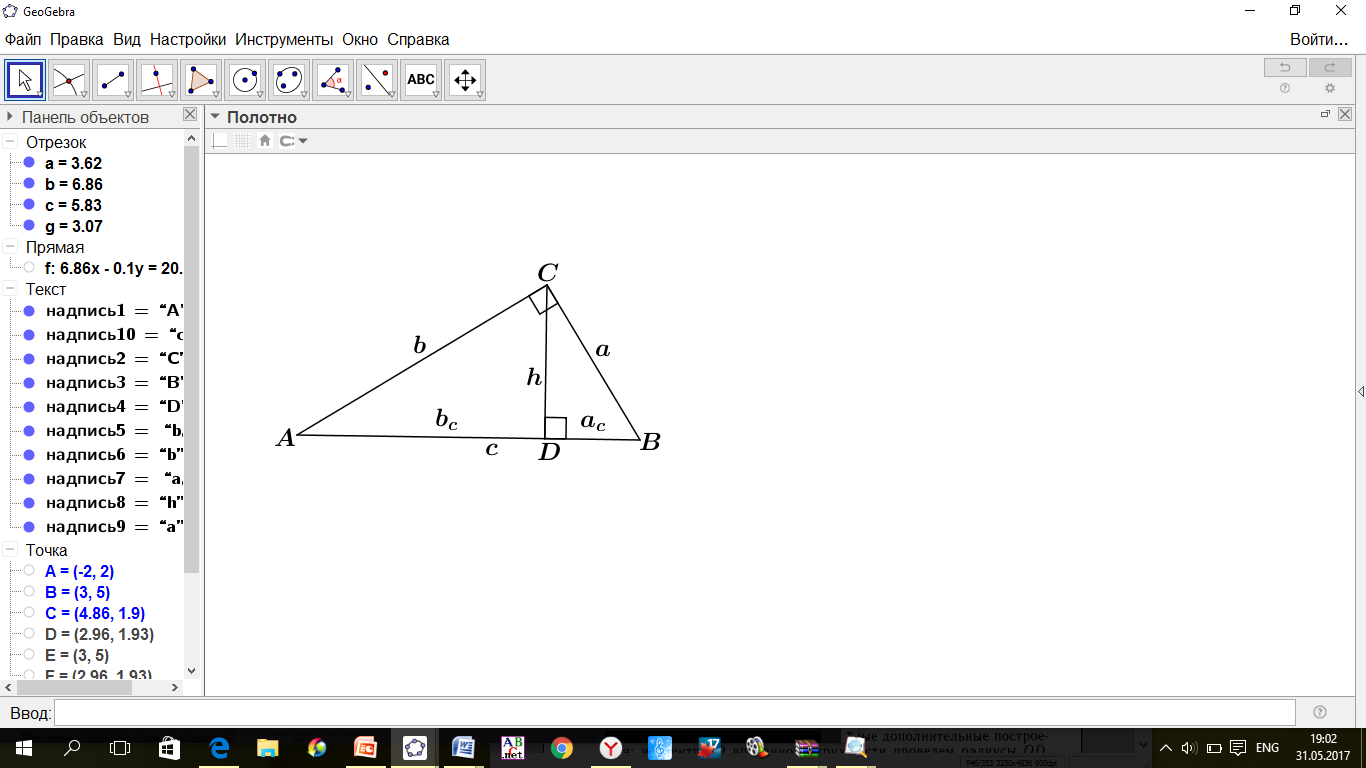 Теорема Пифагора. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Теорема Пифагора. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.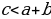
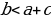
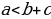
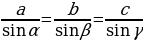
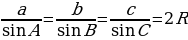
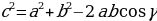
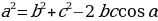
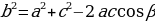
 Через основание и высоту
Через основание и высоту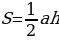
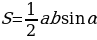
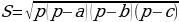
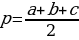
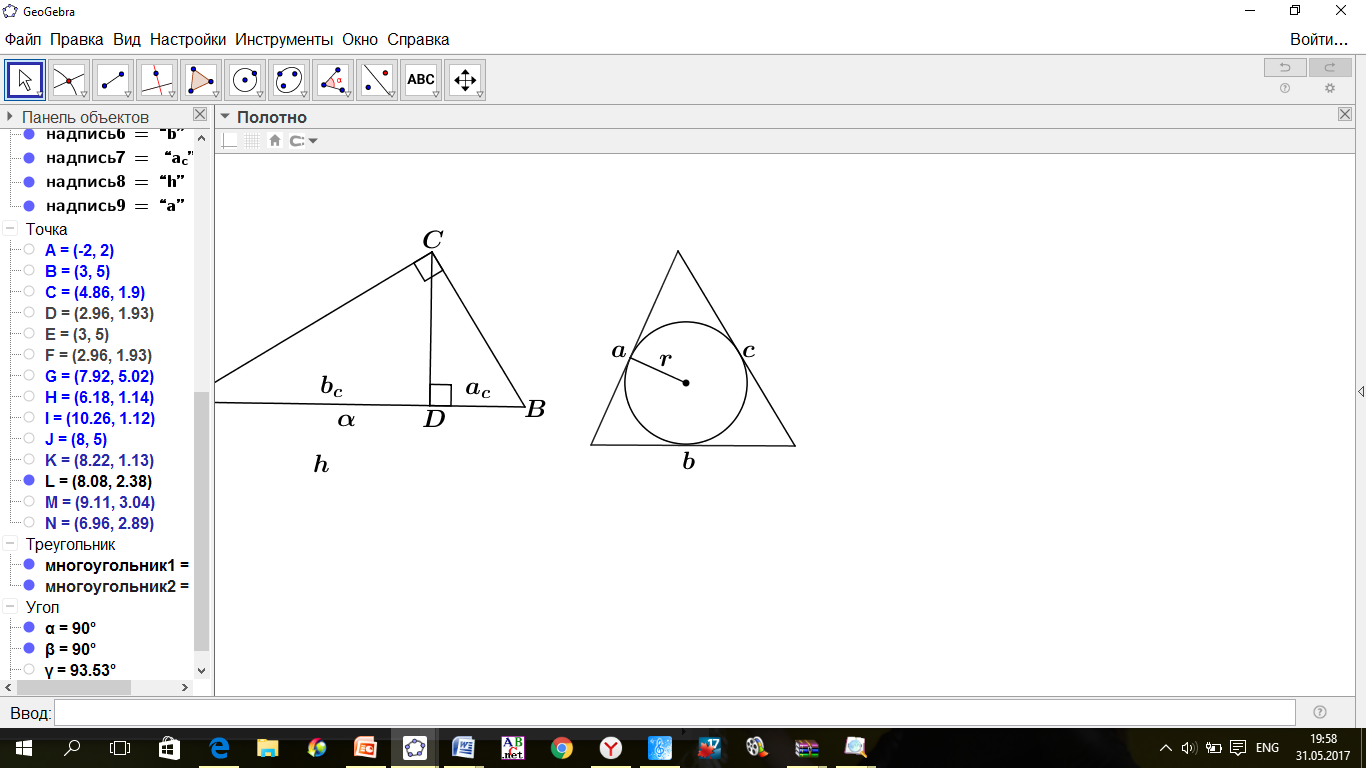 Через радиус вписанной окружности
Через радиус вписанной окружности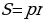
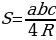
 Следствие. Площадь равностороннего треугольника со стороной
Следствие. Площадь равностороннего треугольника со стороной 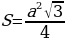 .
.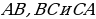 треугольника
треугольника 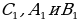 , то отрезки
, то отрезки 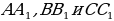 пересекаются в одной точке тогда и только тогда, когда[2]
пересекаются в одной точке тогда и только тогда, когда[2]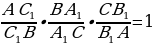
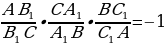
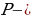 пересечение серединных перпендикуляров, точка
пересечение серединных перпендикуляров, точка 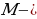 пересечение медианов треугольника, точка
пересечение медианов треугольника, точка 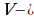 пересечение высот треугольника.
пересечение высот треугольника.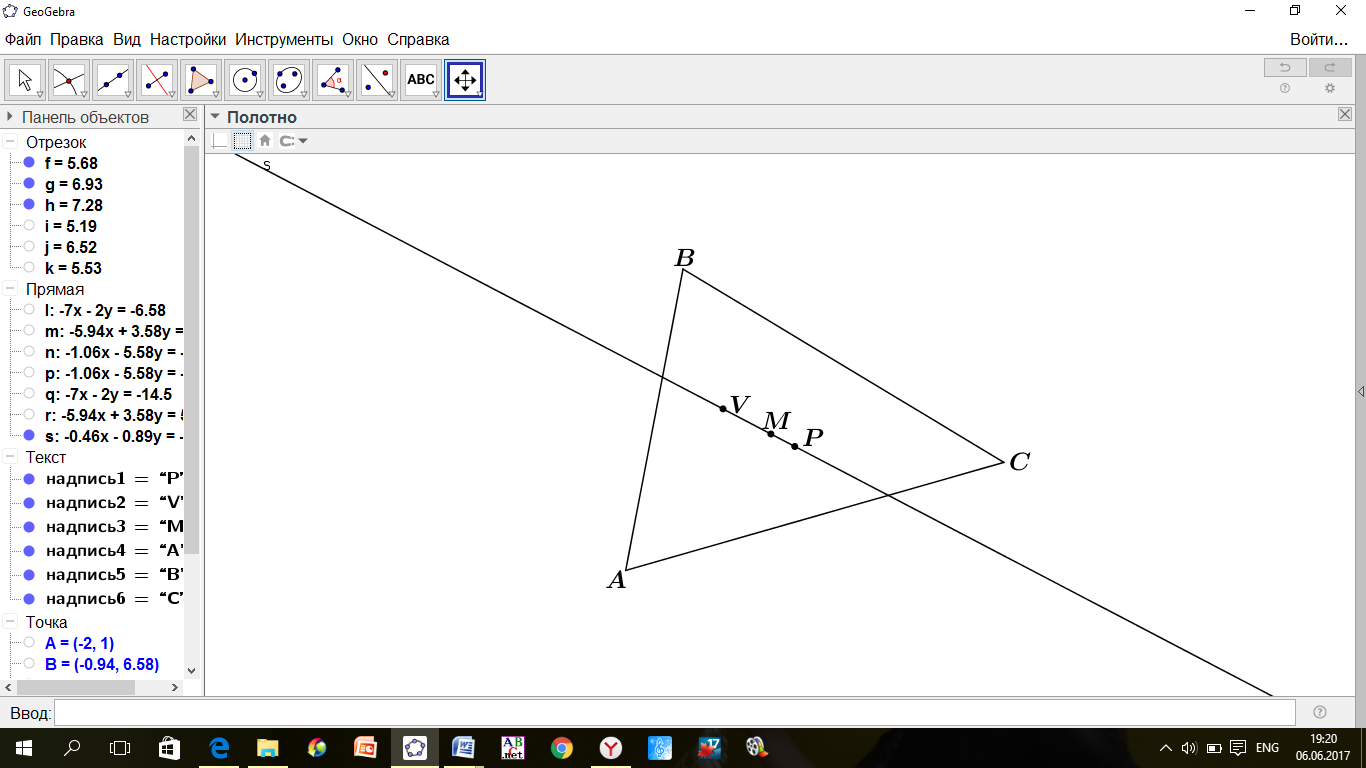
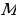 пересечения медиан лежит на отрезке
пересечения медиан лежит на отрезке 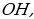 причем
причем 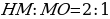
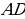 — высота треугольника
— высота треугольника 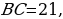
 . Обозначим
. Обозначим  . Поскольку
. Поскольку 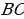 — наибольшая сторона треугольника, точка
— наибольшая сторона треугольника, точка 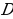 лежит на отрезке
лежит на отрезке 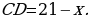 Выразив
Выразив 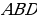 и
и 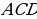 , получим уравнение
, получим уравнение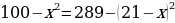 , откуда находим, что
, откуда находим, что 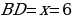 . Следовательно,
. Следовательно, 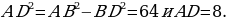
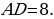
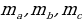 треугольника
треугольника 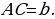 [5]
[5]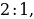 считая от вершины. Поэтому в
считая от вершины. Поэтому в 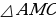 нам известны две стороны:
нам известны две стороны: 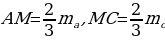 - и медиана
- и медиана 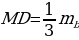 .
.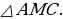 Удвоив его медиану
Удвоив его медиану 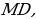 достроим треугольник до параллелограмма
достроим треугольник до параллелограмма 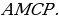 Тогда
Тогда 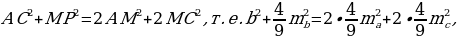 откуда находим:
откуда находим: 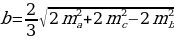 .
.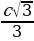 . Найти катет.
. Найти катет.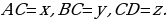 Тогда по теореме Пифагора
Тогда по теореме Пифагора 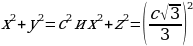 . Кроме того, по теореме о биссектрисе треугольника имеем
. Кроме того, по теореме о биссектрисе треугольника имеем 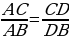 , т.е.
, т.е. 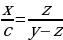 .
.
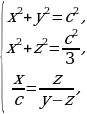
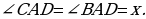 Составим уравнение, использовав отрезок
Составим уравнение, использовав отрезок 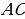 как опорный элемент. Из треугольника
как опорный элемент. Из треугольника 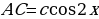 , из треугольника
, из треугольника 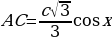 . Приравняв эти выражения, получим тригонометрическое уравнение
. Приравняв эти выражения, получим тригонометрическое уравнение 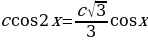 .
.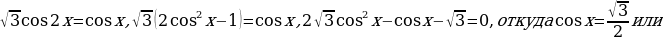
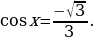
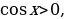 то получаем
то получаем 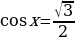 . Значит, угол
. Значит, угол 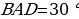 , а угол
, а угол 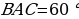 . В итоге получаем
. В итоге получаем 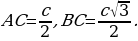
 пересекающиеся в точке
пересекающиеся в точке 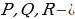 соответственно середины отрезков
соответственно середины отрезков 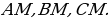 Докажите, что треугольники
Докажите, что треугольники 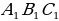 и
и 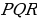 равны.
равны.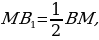 точка
точка 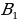 отобразится в точку
отобразится в точку 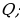
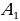 отобразится в точку
отобразится в точку 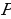 и точка
и точка 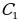 - в точку
- в точку 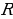 . Треугольники
. Треугольники 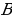 вдвое больше расстояния от центра описанной около треугольника окружности до стороны
вдвое больше расстояния от центра описанной около треугольника окружности до стороны 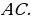
 Пусть
Пусть  остроугольный треугольник, точка
остроугольный треугольник, точка 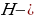 ортоцентр, точка
ортоцентр, точка 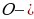 центр описанной окружности, отрезки
центр описанной окружности, отрезки 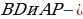 высоты, точки
высоты, точки 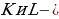 середины сторон,
середины сторон, 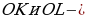 перпендикуляры к сторонам.
перпендикуляры к сторонам. 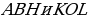 подобны (
подобны (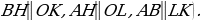
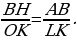 Отрезок
Отрезок 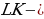 средняя линия
средняя линия 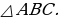 Значит,
Значит, 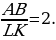 Но тогда
Но тогда 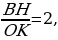 что и требовалось доказать.
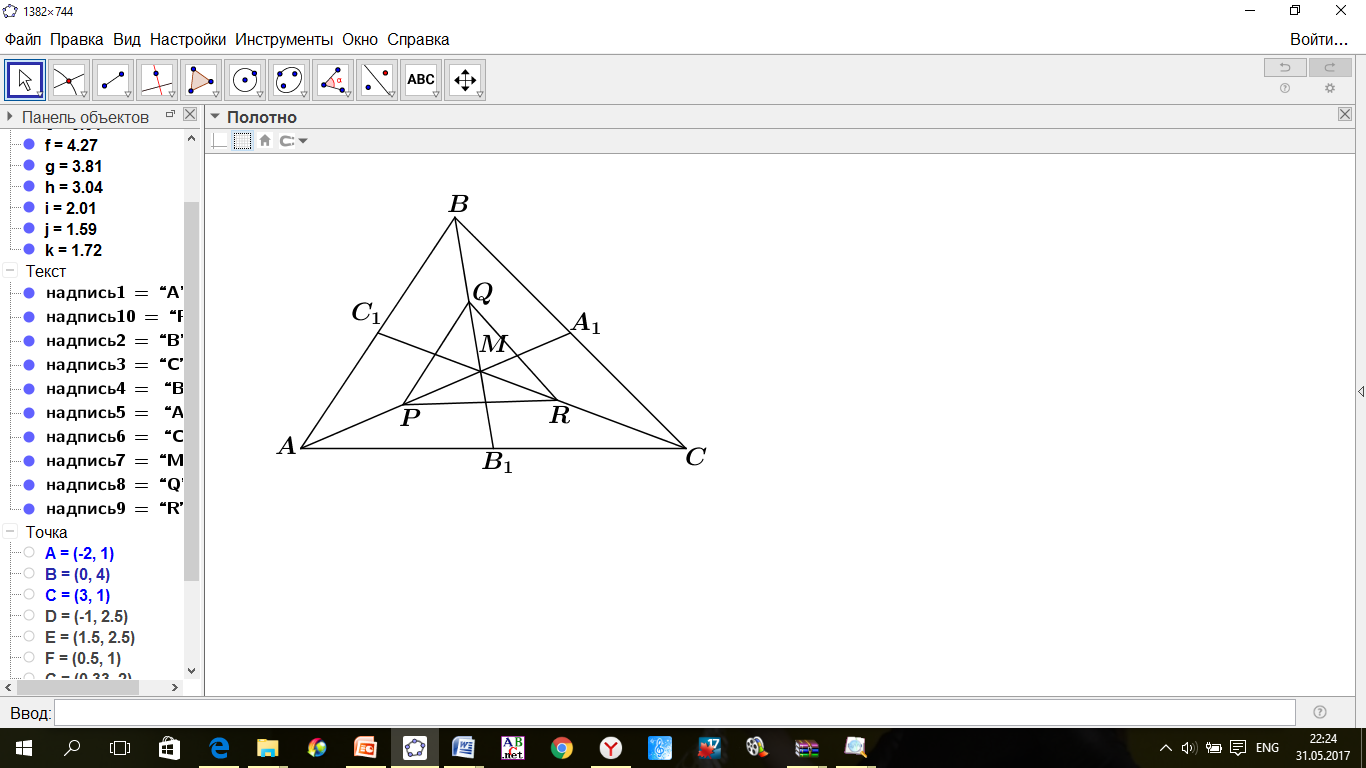
что и требовалось доказать.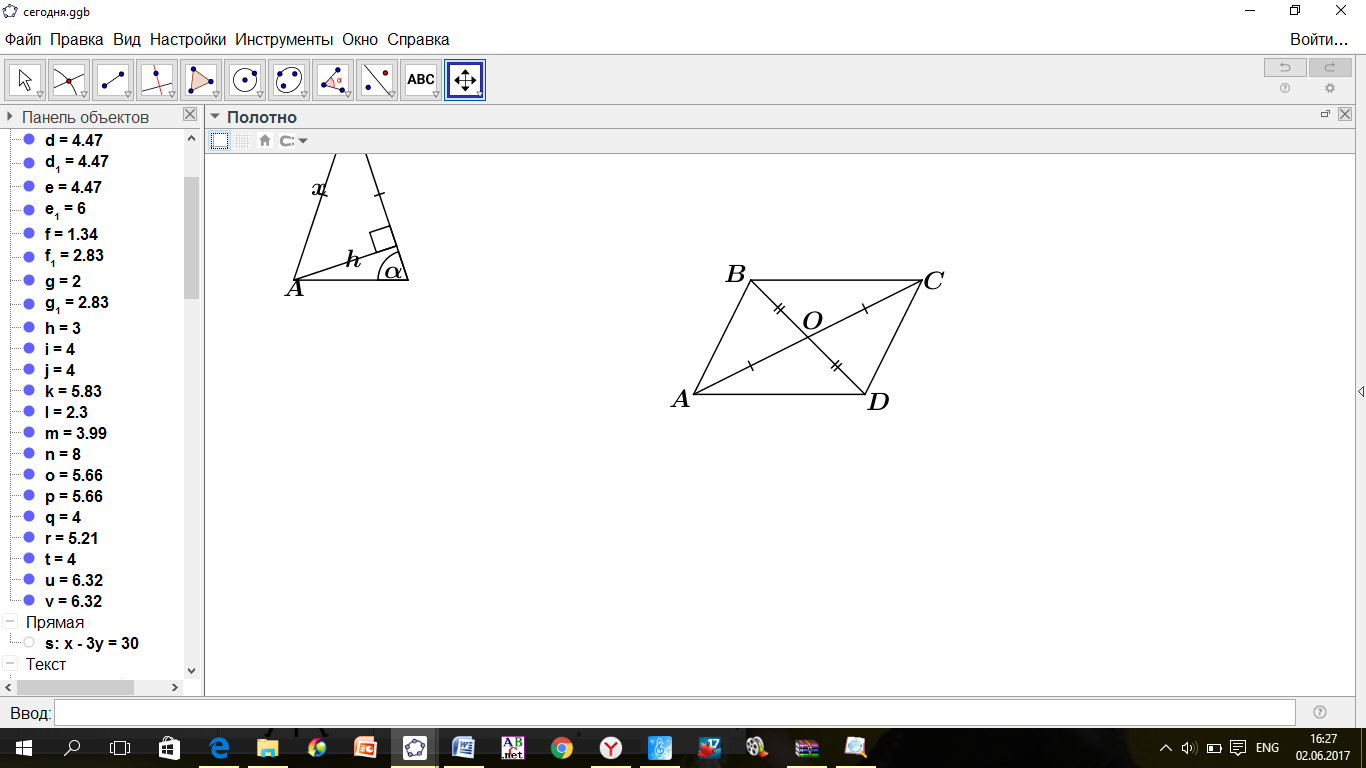 ПРИМЕР 6. Два отрезка
ПРИМЕР 6. Два отрезка 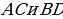 пересекаются в точке
пересекаются в точке 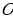 , которая является серединой каждого из них. Докажите равенство треугольников
, которая является серединой каждого из них. Докажите равенство треугольников 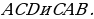
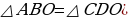
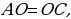
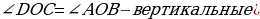 , то есть
, то есть 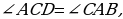 поскольку они являются накрест лежащими при прямых
поскольку они являются накрест лежащими при прямых 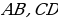 и секущей
и секущей 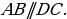 Аналогично доказываем параллельность прямых
Аналогично доказываем параллельность прямых 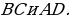 Итак,
Итак, 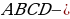 параллелограмм по определению.
параллелограмм по определению. 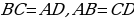 ( в параллелограмме противоположные стороны равны),
( в параллелограмме противоположные стороны равны), 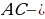 общая для треугольника
общая для треугольника 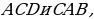 поэтому они равны по трем сторонам. Что и требовалось доказать.
поэтому они равны по трем сторонам. Что и требовалось доказать.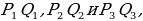 требуется с помощью циркуля и линейки построить треугольник
требуется с помощью циркуля и линейки построить треугольник 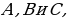 соответственно равны
соответственно равны 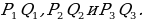

 АНАЛИЗ ЗАДАЧИ. Обозначим через
АНАЛИЗ ЗАДАЧИ. Обозначим через 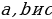 длины сторон искомого треугольника, противолежащих углам
длины сторон искомого треугольника, противолежащих углам 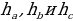 длины отрезков
длины отрезков 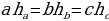 (каждое из произведений равно удвоенной площади треугольника). Из первого равенства получаем пропорцию
(каждое из произведений равно удвоенной площади треугольника). Из первого равенства получаем пропорцию 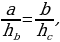 а из второго равенства имеем
а из второго равенства имеем 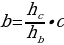 и поэтому
и поэтому 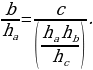
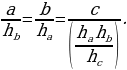
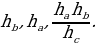
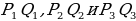 с длинами
с длинами 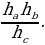 Это можно сделать следующим образом: построим какой-нибудь угол и отложим от его вершины
Это можно сделать следующим образом: построим какой-нибудь угол и отложим от его вершины 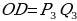 и
и 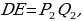 а на другой стороне угла отрезок
а на другой стороне угла отрезок 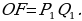
 Проведем прямую
Проведем прямую 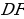 , а затем через точку
, а затем через точку 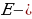 прямую, параллельную
прямую, параллельную 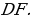 Она пересекает луч
Она пересекает луч 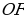 в точке
в точке 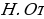 резок
резок 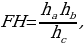 что следует из пропорции
что следует из пропорции 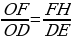 .
.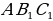 по трем сторонам
по трем сторонам 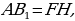
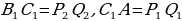 . Этот треугольник, как уже было отмечено, подобен искомому треугольник у. через вершину
. Этот треугольник, как уже было отмечено, подобен искомому треугольник у. через вершину  проведем высоту треугольника
проведем высоту треугольника  , равный
, равный 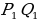 . Через точку
. Через точку 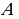 проведем прямую, параллельную
проведем прямую, параллельную 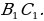 Точки
Точки 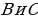 пересечения этой прямой с лучами
пересечения этой прямой с лучами 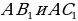 являются вершинами искомого треугольника
являются вершинами искомого треугольника 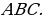
 , как должно быть в искомом треугольнике, т.е. сходственные высоты в треугольнике
, как должно быть в искомом треугольнике, т.е. сходственные высоты в треугольнике 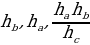 можно было построить треугольник. В таком случае задача имеет решение.
можно было построить треугольник. В таком случае задача имеет решение.  АНАЛИЗ ЗАДАЧИ. Предположим, что искомый равнобедренный треугольник
АНАЛИЗ ЗАДАЧИ. Предположим, что искомый равнобедренный треугольник 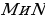 лежат на боковых сторонах
лежат на боковых сторонах  соответственно, данная точка
соответственно, данная точка 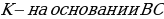 , медиана
, медиана 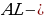 на данной прямой
на данной прямой 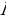 . Поскольку медиана
. Поскольку медиана 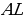 равнобедренного
равнобедренного 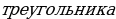
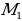 , симметричная точке
, симметричная точке 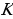 лежит на прямой, перпендикулярной данной прямой
лежит на прямой, перпендикулярной данной прямой 
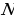 и прямая
и прямая 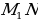 пересекает данную прямую
пересекает данную прямую 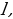 — вторую. Основание искомого треугольника получим, проведя через данную точку
— вторую. Основание искомого треугольника получим, проведя через данную точку 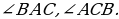 [9]
[9]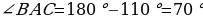 (т.к. смежные углы в сумме дают
(т.к. смежные углы в сумме дают 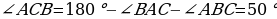 (сумма углов в треугольнике равна
(сумма углов в треугольнике равна 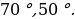
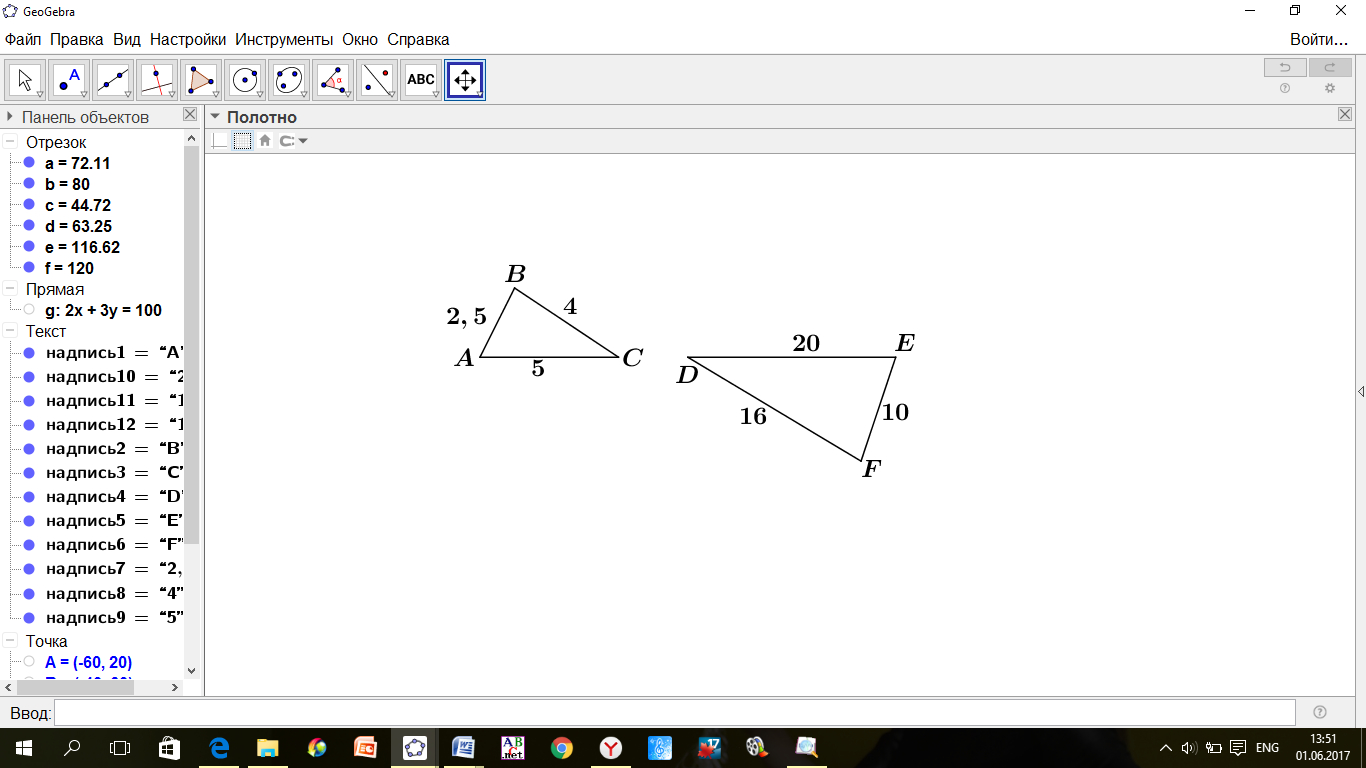
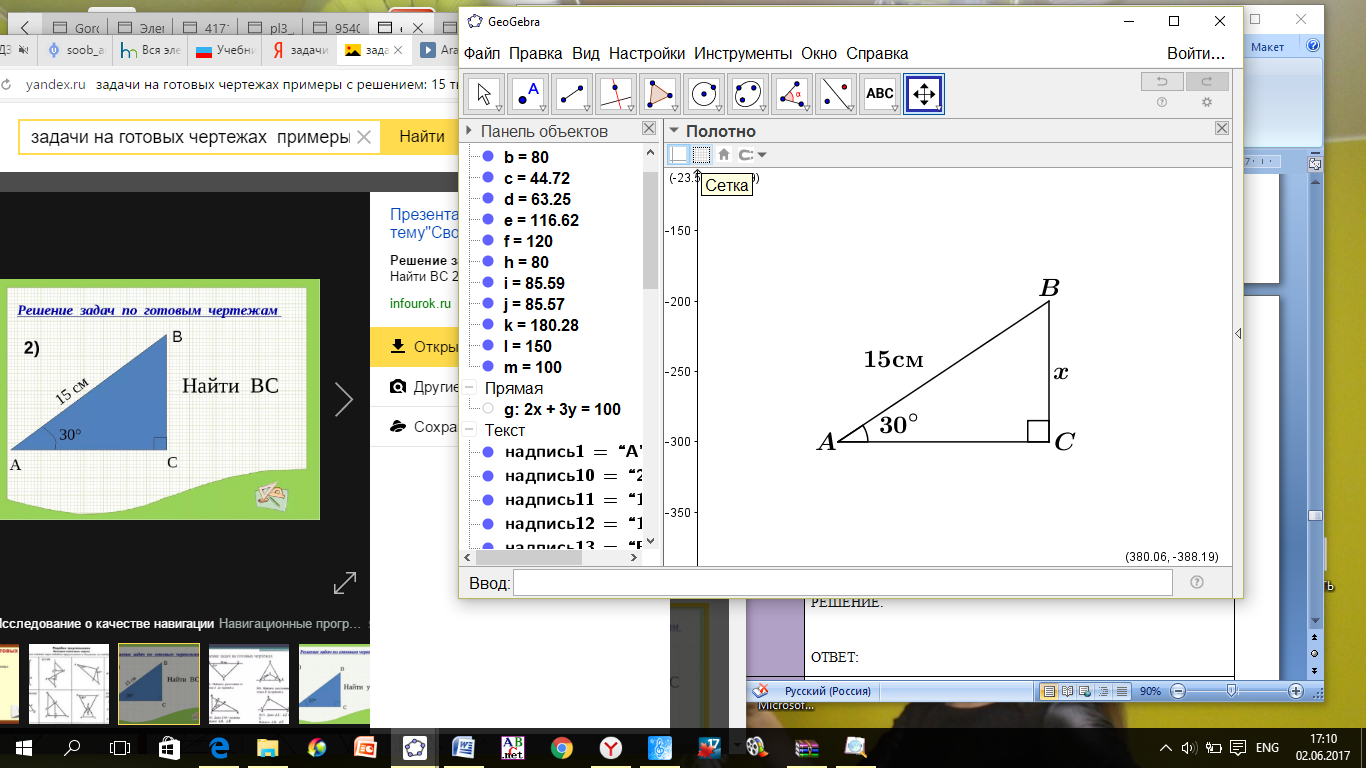 ПРИМЕР 10. Найти
ПРИМЕР 10. Найти 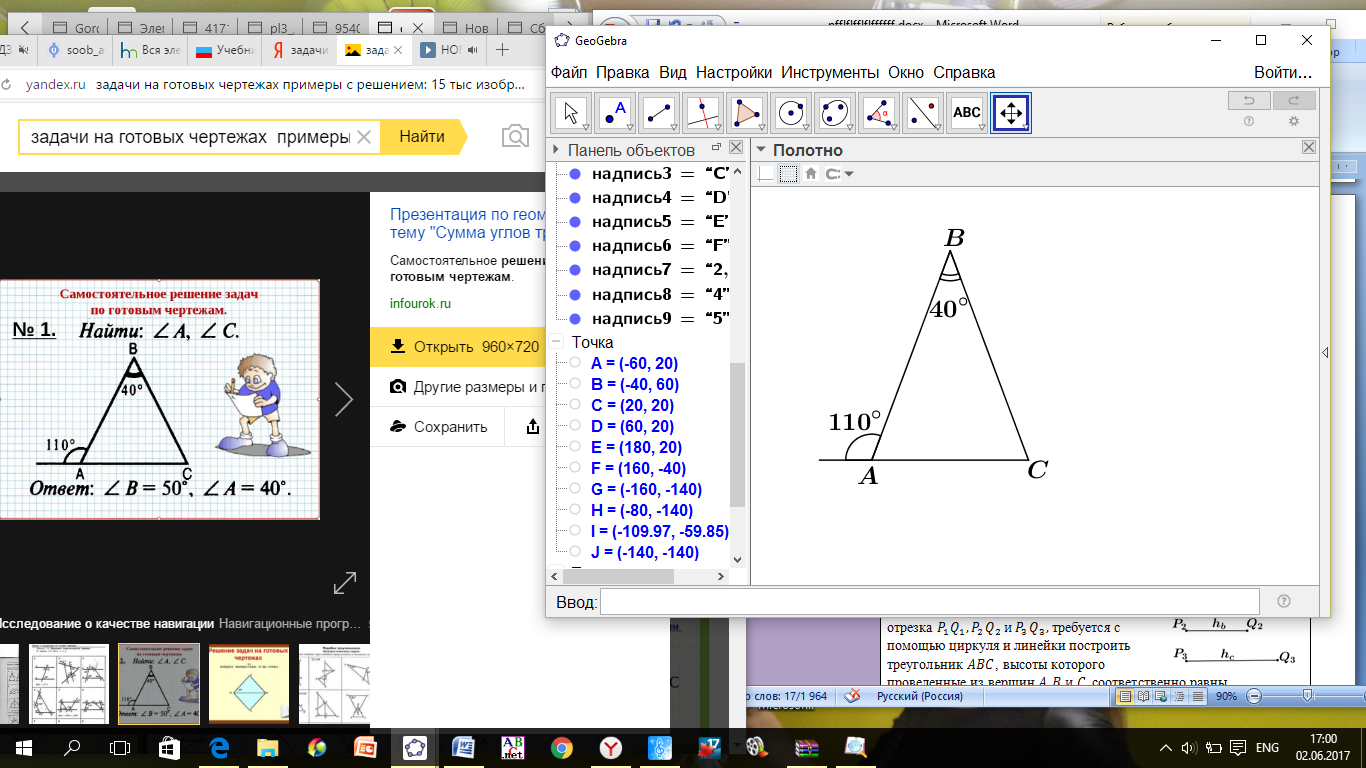 Катет
Катет 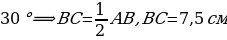 (по свойству прямоугольного треугольника).
(по свойству прямоугольного треугольника).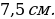
 [8].
[8].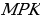 проведен отрезок
проведен отрезок 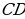 , параллельный
, параллельный 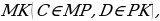
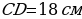 . Найдите
. Найдите 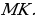
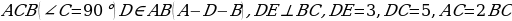 . Найдите площадь треугольника
. Найдите площадь треугольника  , а площадь равна
, а площадь равна 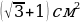 . Найдите меньшую высоту треугольника.[6]
. Найдите меньшую высоту треугольника.[6] проведены высоты
проведены высоты 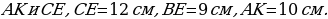 Найдите площадь треугольника
Найдите площадь треугольника 
 см. Найдите радиус вписанной в него окружности.
см. Найдите радиус вписанной в него окружности.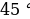 , а высота, проведенная к гипотенузе, равна 9 см. Найдите площадь этого треугольника.
, а высота, проведенная к гипотенузе, равна 9 см. Найдите площадь этого треугольника.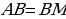 ,
, 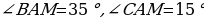 . Найдите углы треугольника
. Найдите углы треугольника 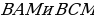 равны тогда и только тогда, когда точка
равны тогда и только тогда, когда точка  [8]
[8] .
.
 равных треугольников
равных треугольников 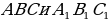 взяты соответственно точки
взяты соответственно точки 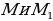 , причем
, причем 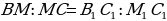 . Докажите, что
. Докажите, что 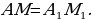
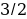 квадрата гипотенузы.
квадрата гипотенузы.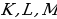 в одном и том же отношении (считая по часовой стрелке). Докажите, что треугольник
в одном и том же отношении (считая по часовой стрелке). Докажите, что треугольник 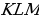 также равносторонний.
также равносторонний.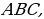 если известны сторона
если известны сторона  и
и 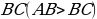 .
.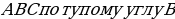 , отношению сторон
, отношению сторон 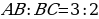 и высоте
и высоте 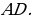
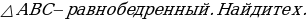 [3]
[3]
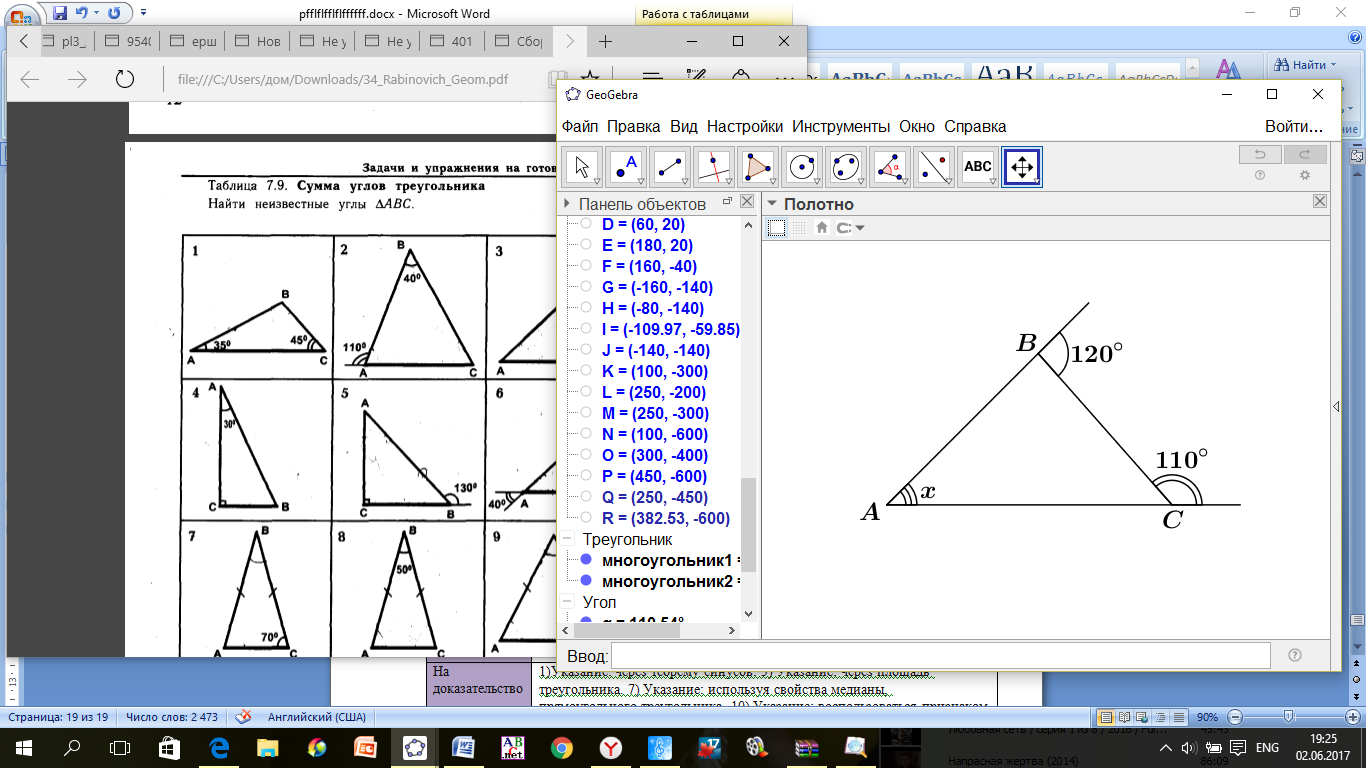
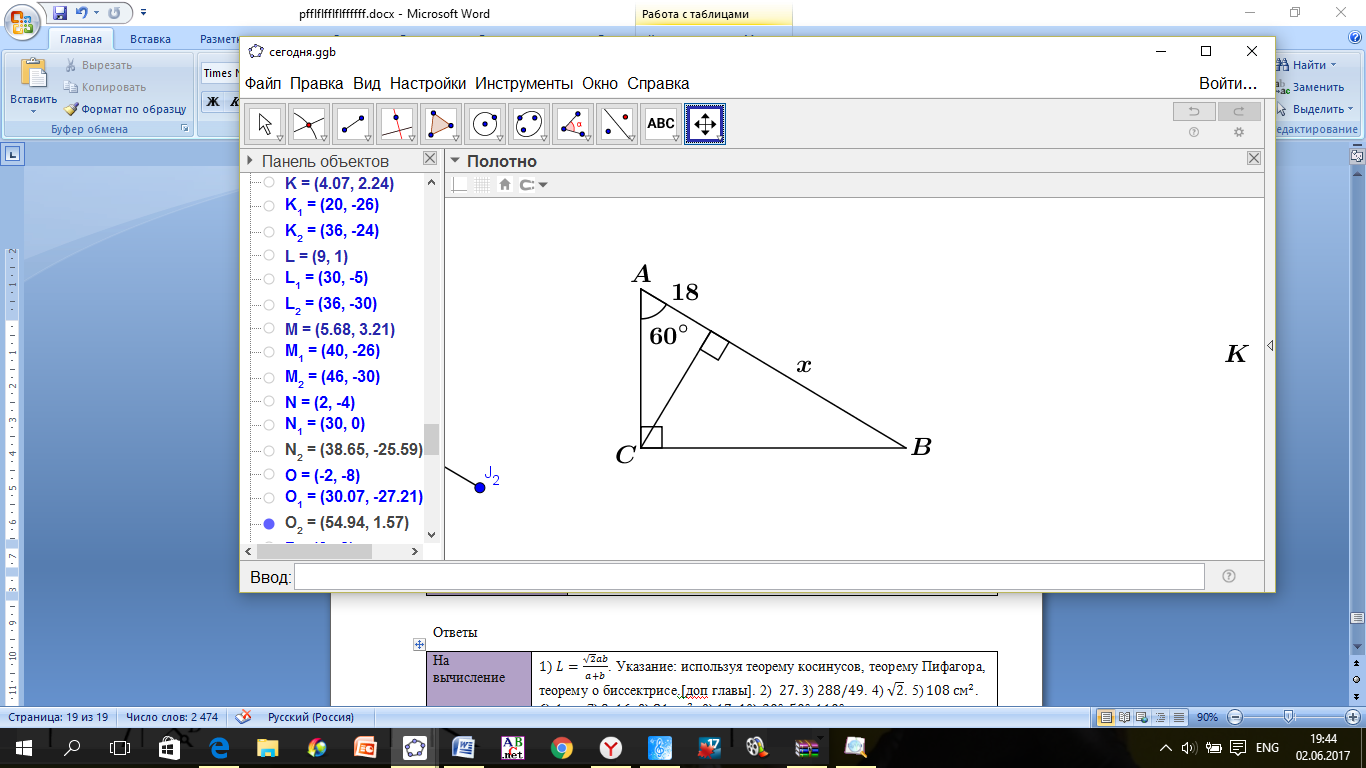
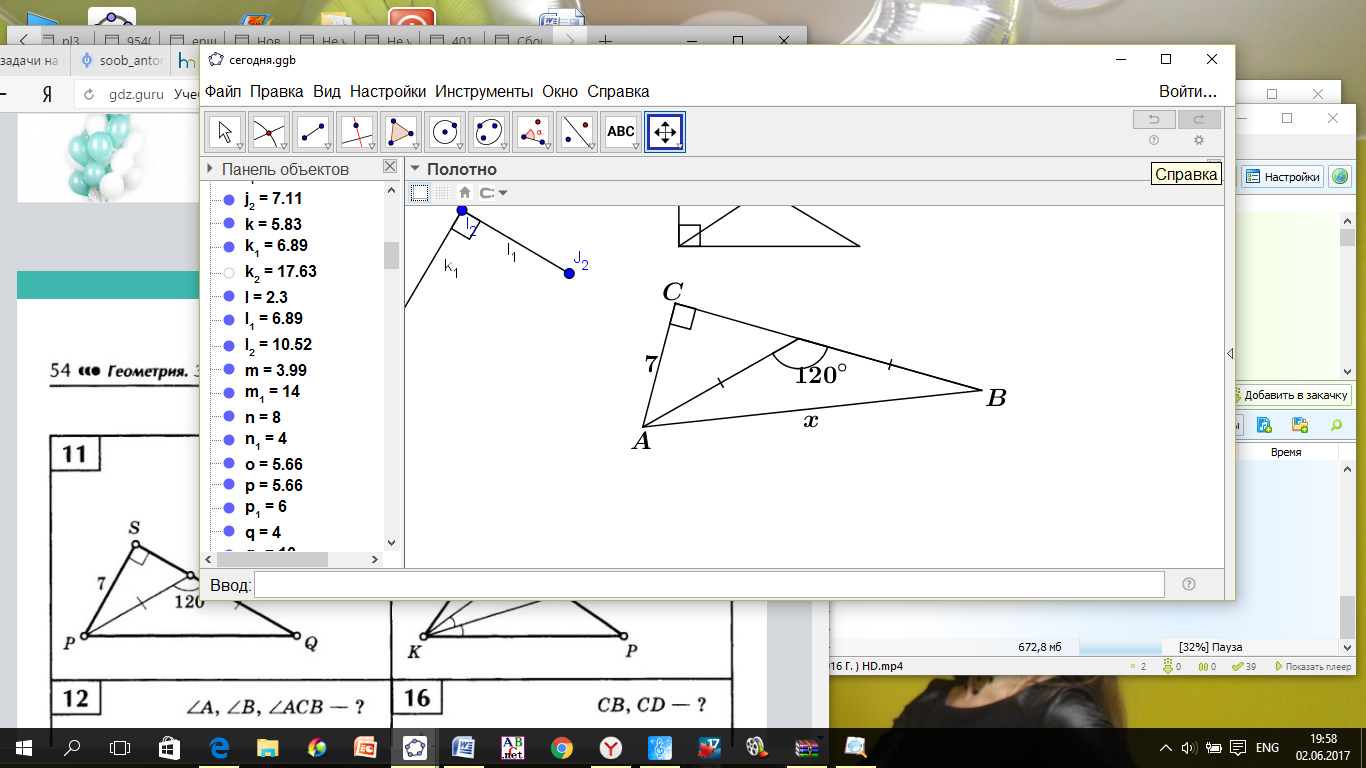
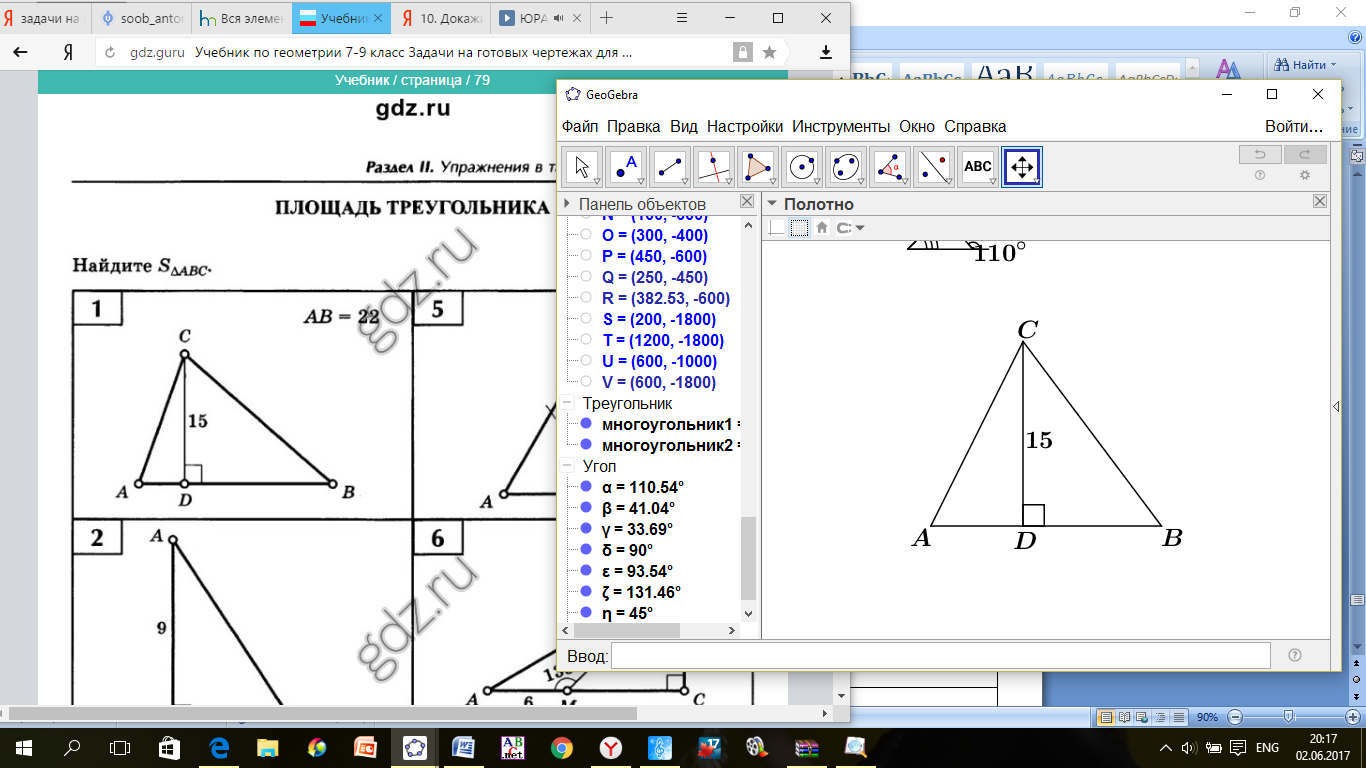
 Найдите
Найдите 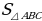 .
.
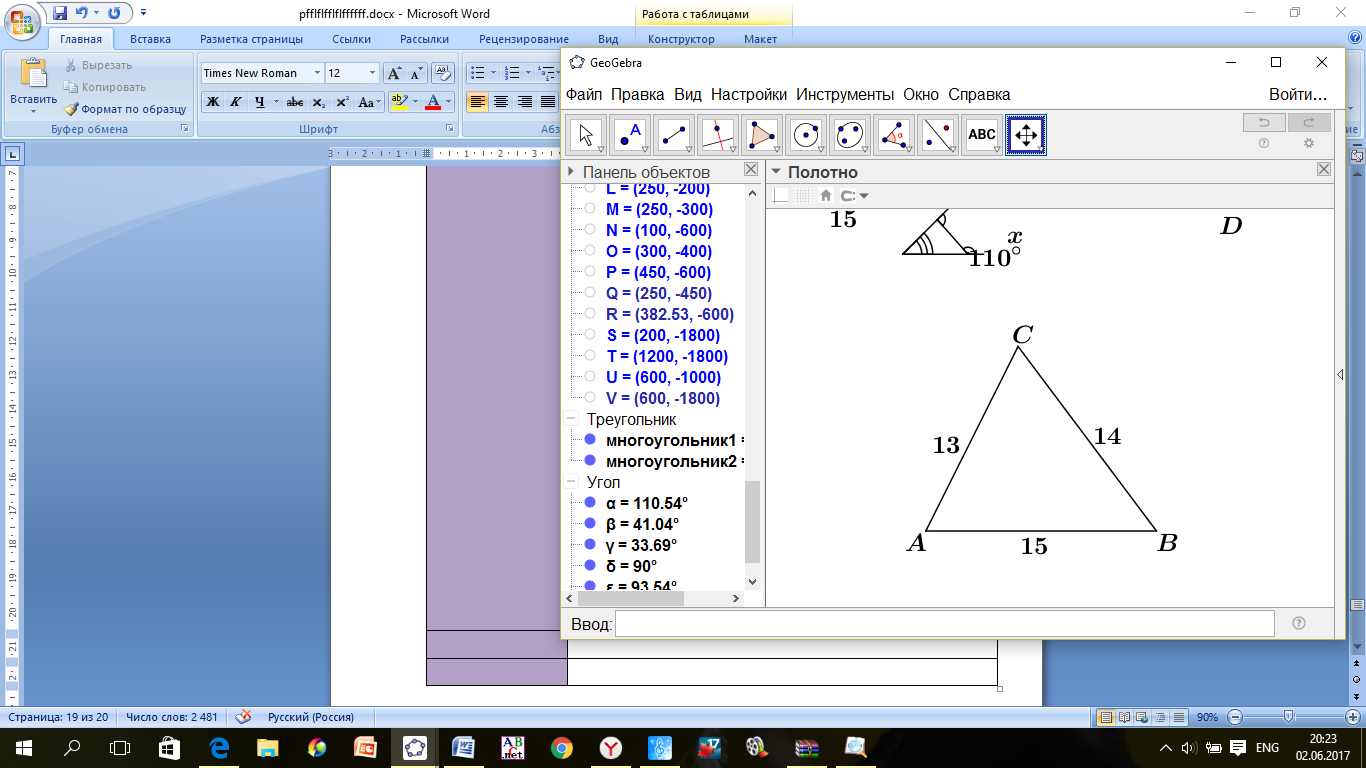
 равносторонний. Найдите
равносторонний. Найдите 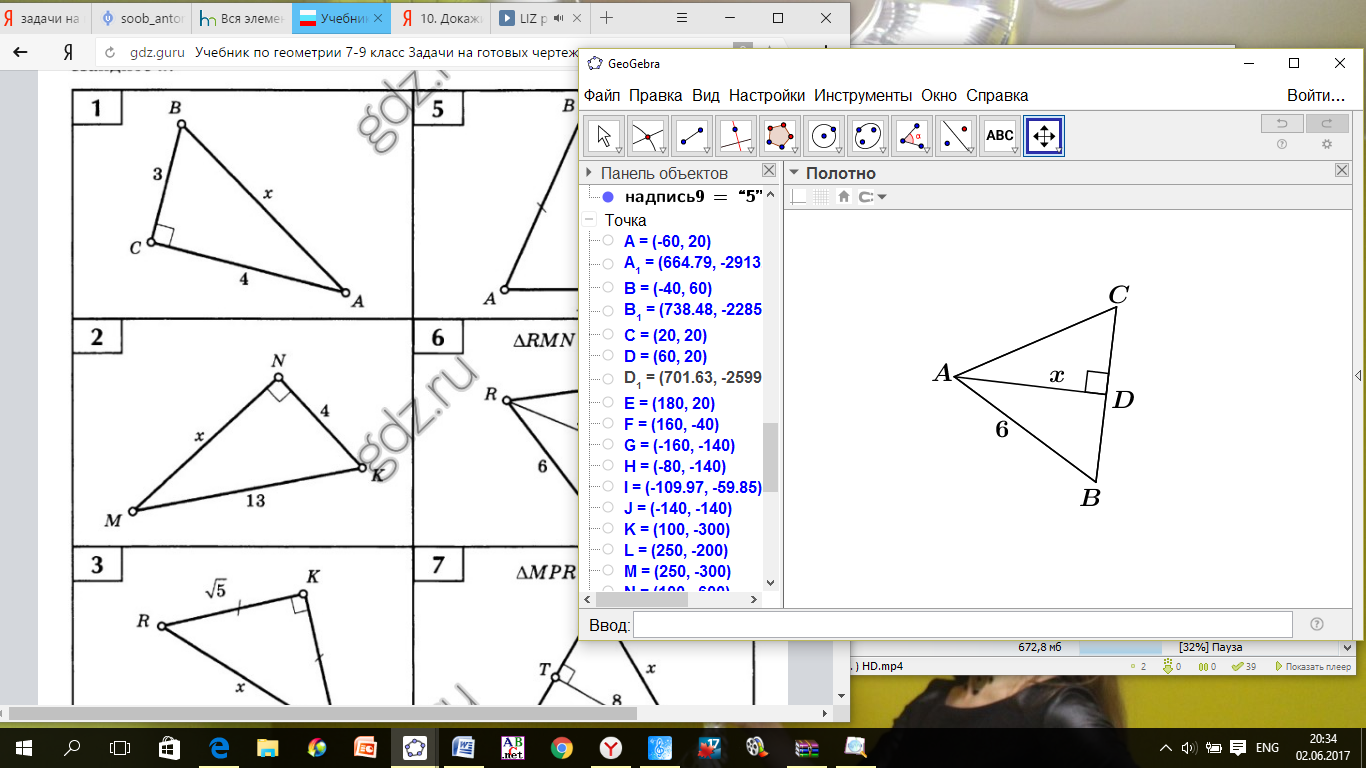
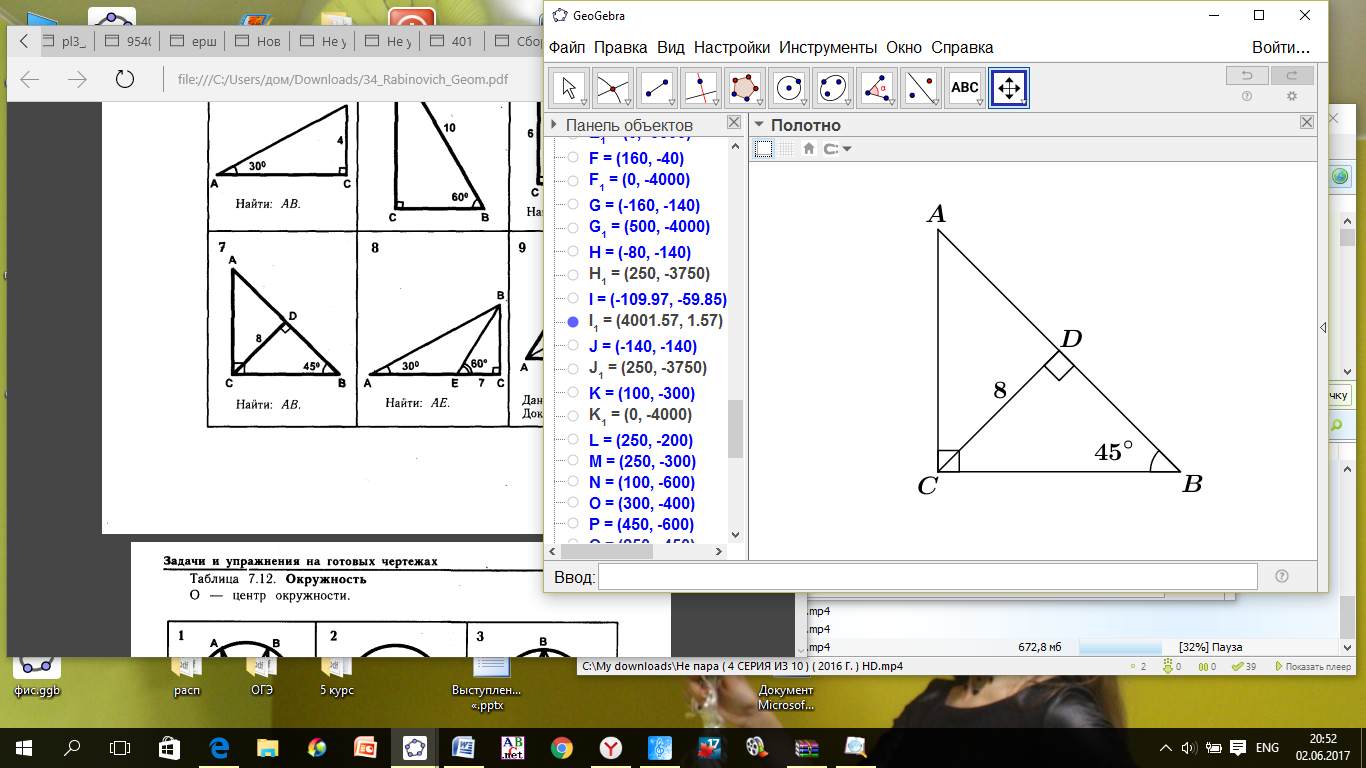
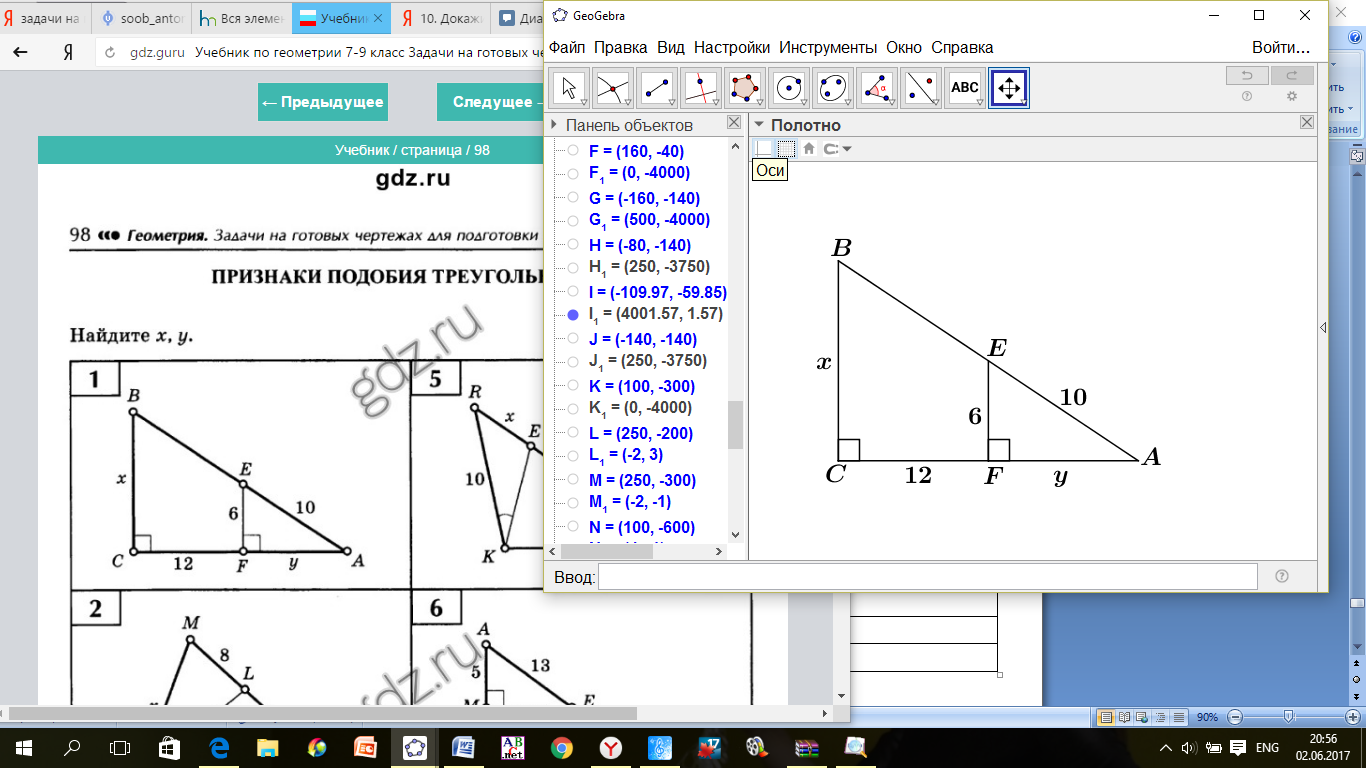
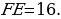 Найдите
Найдите 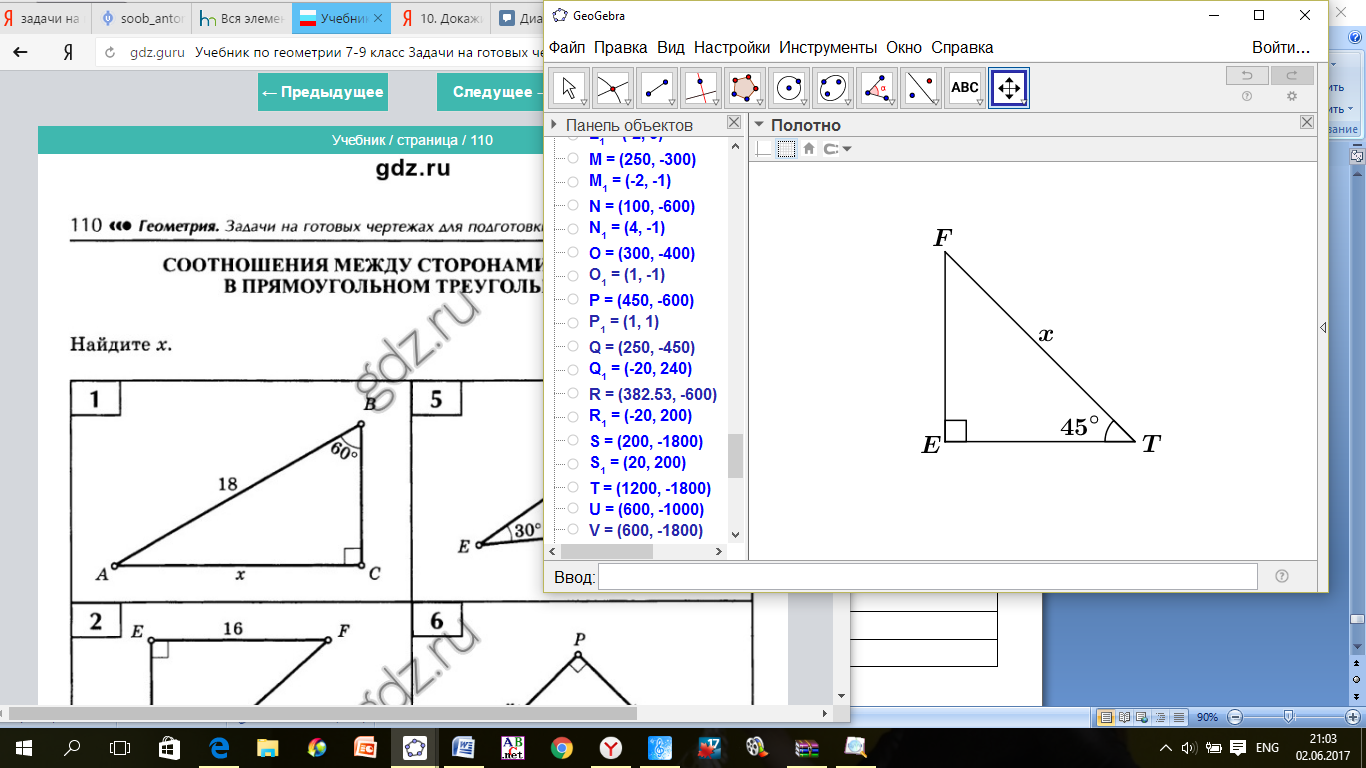
 дрес: Казань, ул. Петербургская, 57
дрес: Казань, ул. Петербургская, 57

 Мост Миллениум (тат. Милленниум күпере) — вантовый мост; самый высокий мост в Казани. Пересекает реку Казанку, соединяя улицу Вишневского с проспектом Амирхана и являясь частью Малого Казанского кольца.
Мост Миллениум (тат. Милленниум күпере) — вантовый мост; самый высокий мост в Казани. Пересекает реку Казанку, соединяя улицу Вишневского с проспектом Амирхана и являясь частью Малого Казанского кольца.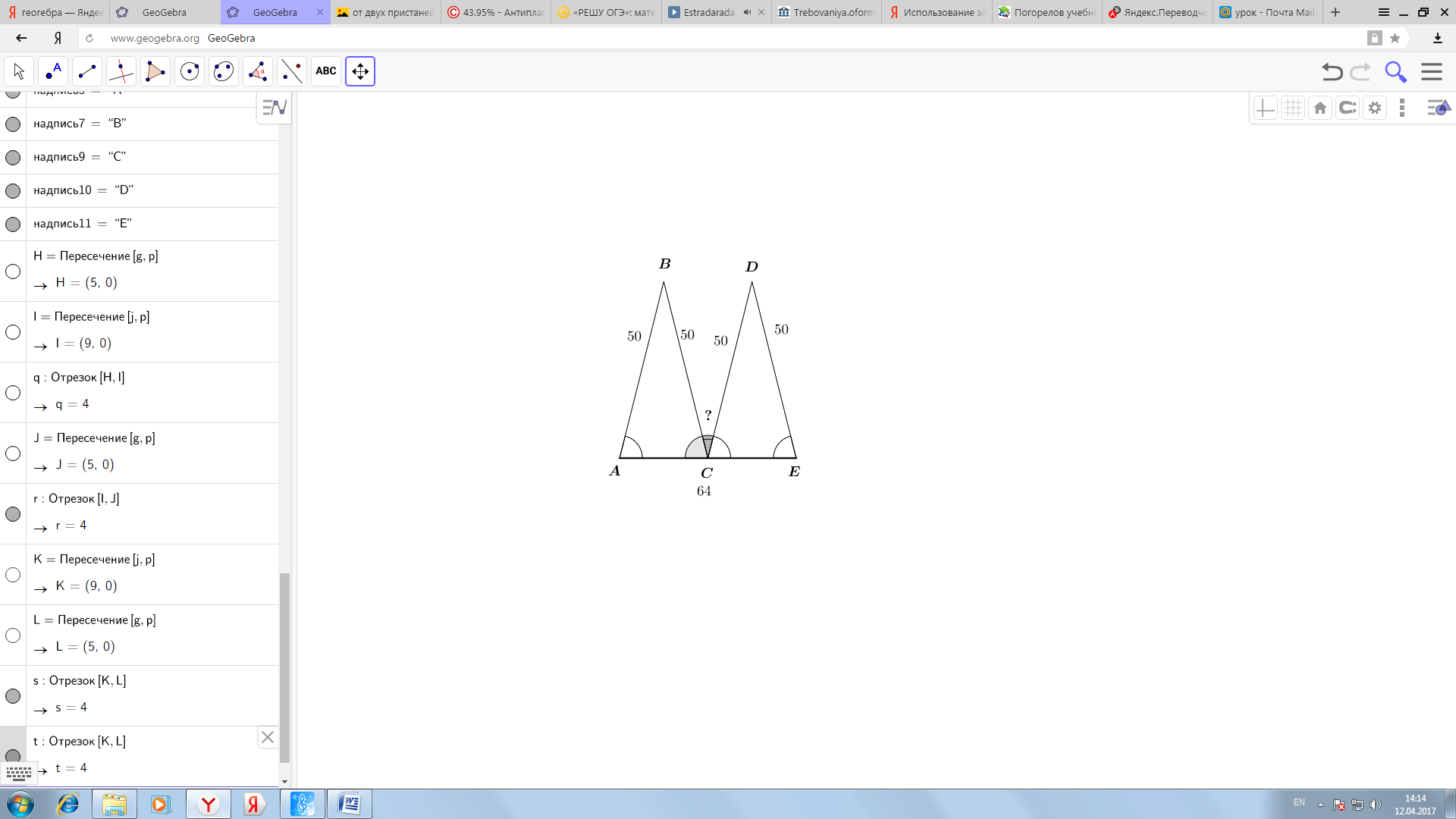
 Территория парка ограничена улицами Салимжанова с юга, Артёма Айдинова с востока (у Баскет-холла) и Островского с севера. С запада к парку примыкает главное здание ОАО «Татэнерго».
Территория парка ограничена улицами Салимжанова с юга, Артёма Айдинова с востока (у Баскет-холла) и Островского с севера. С запада к парку примыкает главное здание ОАО «Татэнерго». Адрес: Казань, просп. Фатыха Амирхана, 1
Адрес: Казань, просп. Фатыха Амирхана, 1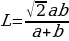 Указание: используя теорему косинусов, теорему Пифагора, теорему о биссектрисе.
Указание: используя теорему косинусов, теорему Пифагора, теорему о биссектрисе.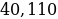 .
.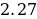 .
.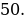
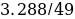 .
.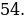
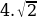 .
.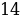 .
.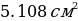 .
.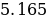 .
.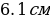 .
.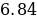 .
.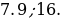
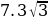 .
.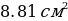 .
.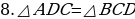 .
.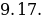
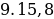 .
.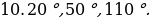
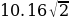 .
.