Геометрия 8 класс.Контрольные работы.

Контрольная работа № 1

Вариант I.

1. На сторонах АВ и ВС треугольника АВС отмечены точки N и M так, что NM || АС. Докажите, что NBM ~ АВС.

2. Прямоугольные треугольники ABF (А = 90°) и СDF (C = 90°) подобны. Известно, что AF = 18 см, АВ = 6 см, DC = 12 см. Определите коэффициент подобия.

3. Основание ВС трапеции АВСD равно 9 см. О – точка пересечения диагоналей трапеции. Найдите основание АD, если АО : ОС = 4 : 3.

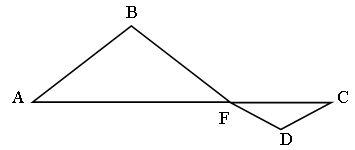
4. На рисунке СВА = 37°. Найдите угол GEF.

5. В треугольнике АВС проведены высоты АD и BF, которые пересекаются в точке G. Докажите, что AGF ~ ВСF.

Вариант II.

1. В прямоугольном треугольнике АВС (С – прямой) проведена высота СD. Докажите, что ACD ~ AВС.

2. Равнобедренные треугольники АBF и СDF подобны, причем АВ = BF и АВ || DC. Известно, что AF = 20 см, AB = 12 cм, DC = 4 см. Определите коэффициент подобия.

3. Из вершины D параллелограмма АВСD проведены прямая, пересекающая сторону ВС в точке G, и диагональ АС. О – точка их пересечения, GC = 14 см. Найдите сторону AD, если GO : OD = 7 : 10.

4. На рисунке точки О и О₁ – центры окружностей. Найдите угол DBC.

5. Сумма углов при основании трапеции равна 90°. Докажите, что высота трапеции есть среднее пропорциональное между проекциями ее боковых сторон на основание.

КОНТРОЛЬНАЯ РАБОТА №2

Вариант I.

1. В треугольнике АВС сторона АВ равна 11 см, ВАС = 45°, АСВ = 30°. Найдите сторону ВС.

2. Найдите сторону треугольника, лежащую против угла в 135°, если две другие стороны равны см и 3 см.

3. Докажите, что если точка К лежит на стороне СВ прямоугольного треугольника АВС (С = 90°), то АК АС.

4. Сторона параллелограмма равна см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30°, равна 6 см.

5*. Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.

Вариант I.

1. В треугольнике АВС сторона АВ равна 11 см, ВАС = 45°, АСВ = 30°. Найдите сторону ВС.

2. Найдите сторону треугольника, лежащую против угла в 135°, если две другие стороны равны см и 3 см.

3. Докажите, что если точка К лежит на стороне СВ прямоугольного треугольника АВС (С = 90°), то АК АС.

4. Сторона параллелограмма равна см. Найдите его углы, если диагональ, образующая с другой стороной угол в 30°, равна 6 см.

5*. Диагональ прямоугольника делит его угол на два угла в отношении 1:2. Найдите отношение сторон прямоугольника.

Вариант II.

1. В треугольнике GED сторона GF равна 13 см, FDG = 45°, DGF = 60°. Найдите сторону FD.

2. Найдите сторону треугольника, лежащую против угла в 150°, если две другие стороны равны и 7 см.

3. Докажите, что если точка N лежит на стороне СВ равностороннего треугольника АВС (С = 90°), то AN

4. Найдите углы равнобокой трапеции, в которой боковая сторона равна см, а диагональ, равная 4 см, образует с основанием угол в 30°.

5*. Диагональ параллелограмма делит один из его углов на два угла, равные 45° и 30°. Найдите отношение сторон параллелограмма

Контрольная работа № 3

Вариант I.

1. Сколько сторон имеет многоугольник, если сумма его углов равна 1620°?

2. В окружность вписан правильный шестиугольник со стороной, равной 9 см. Найдите длину дуги окружности, стягиваемой стороной шестиугольника.

3. Найдите длину окружности, описанной около правильного треугольника, если радиус вписанной в этот треугольник окружности равен 7 см.

4. В правильном шестиугольнике ABCDFG проведены диагонали ВС и CF. Докажите, что четырехугольник BCFG – прямоугольник, и выразите его стороны через сторону шестиугольника.

5. Около окружности описан многоугольник, все углы которого равны. Является ли данный многоугольник правильным?

Вариант I.

1. Сколько сторон имеет многоугольник, если сумма его углов равна 1620°?

2. В окружность вписан правильный шестиугольник со стороной, равной 9 см. Найдите длину дуги окружности, стягиваемой стороной шестиугольника.

3. Найдите длину окружности, описанной около правильного треугольника, если радиус вписанной в этот треугольник окружности равен 7 см.

4. В правильном шестиугольнике ABCDFG проведены диагонали ВС и CF. Докажите, что четырехугольник BCFG – прямоугольник, и выразите его стороны через сторону шестиугольника.

5. Около окружности описан многоугольник, все углы которого равны. Является ли данный многоугольник правильным?

II вариант.

1. Сколько сторон имеет многоугольник, если сумма его углов равна 1980°?

2. В окружность вписан квадрат со стороной, равной 8 см. Найдите длину дуги окружности, стягиваемой стороной квадрата.

3. Найдите длину окружности, вписанной в правильный треугольник, если радиус описанной около этого треугольника окружности равен 8 см.

4. В правильном восьмиугольнике ABCDEFGH проведены диагонали СН и DG. Докажите, что четырехугольник CDGH – прямоугольник, и выразите его стороны через сторону восьмиугольника.

5. Около окружности описан многоугольник, все стороны которого равны. Является ли данный многоугольник правильным?

контрольная работа № 4

Вариант I.

1. Найдите площадь параллелограмма, если одна из его сторон равна 6 см, а высота, проведенная к этой стороне, равна 9 см.

2. Найдите площадь правильного треугольника со стороной 8 см.3. В равнобокой трапеции с боковой стороной, равной  см, меньшее основание равно 4 см, угол при большем основании составляет 45°. Найдите площадь трапеции.

4. На стороне АВ параллелограмма ABCD отмечена произвольная точка G. Докажите, что сумма площадей треугольников ACG и BDG равна половине площади этого параллелограмма.

5. Найдите площадь описанного около окружности правильного треугольника, если площадь вписанного в эту окружность квадрата равна см².

Вариант II.

1. Найдите площадь трапеции, если ее основания равны 7 см и 11 см, а высота равна 4 см.

2. Найдите площадь равнобедренного прямоугольного треугольника, если его катет равен 8 см.

3. Меньшая диагональ ромба равна см, один из углов равен 60°. Найдите площадь ромба.

4. Внутри параллелограмма ABCD отмечена произвольная точка G. Докажите, что сумма площадей треугольников CGD и АGВ равна половине площади этого параллелограмма.

5. Найдите площадь описанного около окружности квадрата, если площадь вписанного в эту окружность правильного шестиугольника равна см².

Вариант I.

1. Найдите площадь параллелограмма, если одна из его сторон равна 6 см, а высота, проведенная к этой стороне, равна 9 см.

2. Найдите площадь правильного треугольника со стороной 8 см.3. В равнобокой трапеции с боковой стороной, равной  см, меньшее основание равно 4 см, угол при большем основании составляет 45°. Найдите площадь трапеции.

4. На стороне АВ параллелограмма ABCD отмечена произвольная точка G. Докажите, что сумма площадей треугольников ACG и BDG равна половине площади этого параллелограмма.

5. Найдите площадь описанного около окружности правильного треугольника, если площадь вписанного в эту окружность квадрата равна см².