Просмотр содержимого документа
«Геометрия – грамматика архитектора»
Геометрия – грамматика архитектора
Одним из самых увлекательных и важных разделов математики является геометрия. Геометрия, как ни один другой предмет, нужна каждому человеку, поскольку именно она дает необходимые пространственные представления. Школьный курс геометрии делится на две части: планиметрию, в которой рассматриваются свойства фигур на плоскости, и стереометрию, в которой рассматриваются свойства фигур в пространстве. В старшей школе изучают стереометрию. В 10 классе общеобразовательной школы на ее изучение отводится 1,5 часа в неделю. За столь малое количество времени учителю надо в доступной форме ответить на вопрос: зачем изучать стереометрию?
Во-первых, стереометрия знакомит с разнообразием пространственных фигур, законами их восприятия и изображения, что позволяет правильно ориентироваться в окружающем нас мире.
Во-вторых, стереометрия способствует развитию логического мышления, приобретению необходимых практических навыков в моделировании и конструировании пространственных фигур.
В-третьих, стереометрия изучает красивые математические объекты, многие из которых придумал не сам человек, их создала природа. Например, кристаллы - природные многогранники. Формы правильных многогранников находят широкое применение в живописи, скульптуре, архитектуре, строительстве.
Плоское изображение способно передать впечатление о трехмерном предмете. Но при этом могут возникнуть даже иллюзии. В живописи существует целое направление «импоссибилизм» - изображение невозможных фигур, парадоксов. Современный шведский архитектор О. Рутерсвард посвятил невозможным объектам серию своих художественных работ.
Пространственные фигуры на чертеже изображаются в виде плоских фигур. Для этого используется параллельное проектирование. Очень важно уметь правильно изображать плоские фигуры, поскольку они входят в поверхности основных пространственных фигур. Плоские многоугольники являются гранями многогранников, круги – основаниями цилиндров и конусов.
Перед учителем встает проблема изложить материал кратко, компактно, наглядно. На первых уроках геометрии в 10 классе (учебник Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.) с целью повторения аксиом планиметрии и изучения аксиом стереометрии можно рассмотреть сравнительные таблицы.
|
|
|
| Планиметрия (плоский) | Стереометрия (объемный) |
| Основные понятия | т очка, прямая очка, прямая ● | т  очка, прямая, плоскость очка, прямая, плоскость ● |
| Примеры фигур 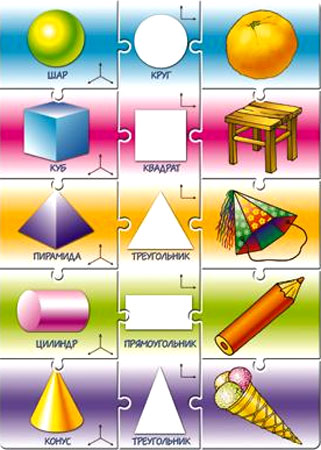
| О трезок, луч, угол, треугольник, многоугольник, окружность, круг ● трезок, луч, угол, треугольник, многоугольник, окружность, круг ● ● ● ● ●      | Многогранники (куб, параллелепипед, призма, пирамида), тела вращения (сфера и шар, цилиндр, конус) 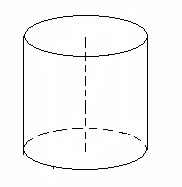 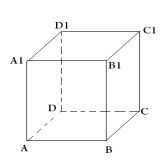 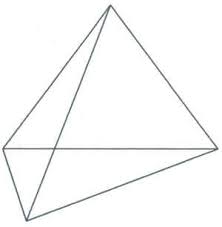 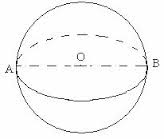 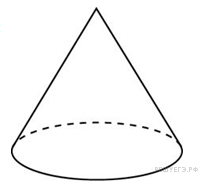
|
| Аксиомы (взаимное расположение точек , прямых и плоскостей) | 1. Каждой прямой принадлежат по крайней мере две точки. 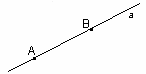
| 1. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. 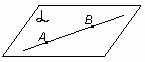
|
| 2. Имеются по крайней мере три точки, не лежащие на одной прямой. 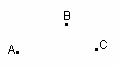
| 2. Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна. 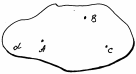
|
| 3.Через любые две точки проходит прямая, и притом только одна.  Две прямые либо имеют только одну общую точку, либо не имеют общих точек. 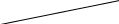 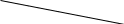 ● О
| 3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. 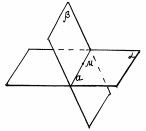
|
Параллельность прямых
|
| Планиметрия (плоский) | Стереометрия (объемный) |
| Определение | Две прямые на плоскости называются параллельными, если они не пересекаются.   а в | Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. 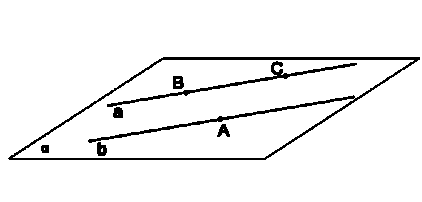
|
| Аксиомы Теоремы | 1. Через любую точку плоскости, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. 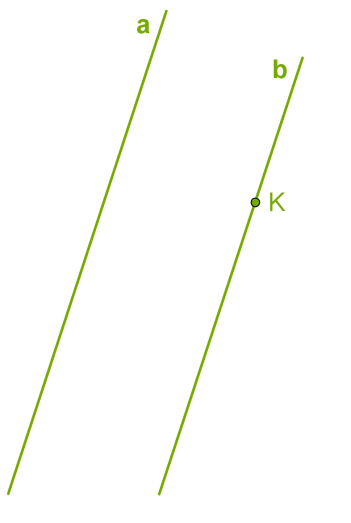
| 1. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. 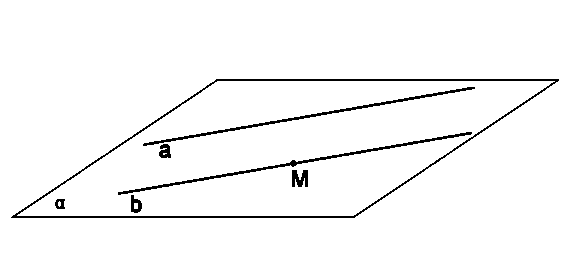
|
| 2. Если две прямые параллельны третьей прямой, то они параллельны. 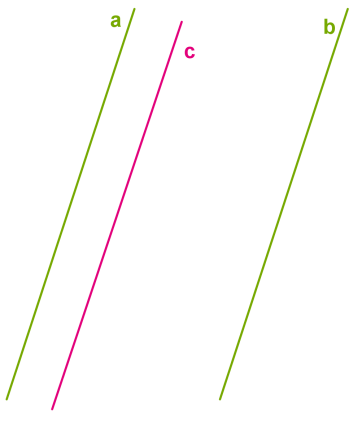
| 2. Если две прямые параллельны третьей прямой, то они параллельны. 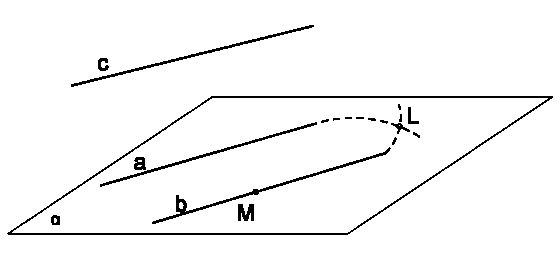
|
|
| 3. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. 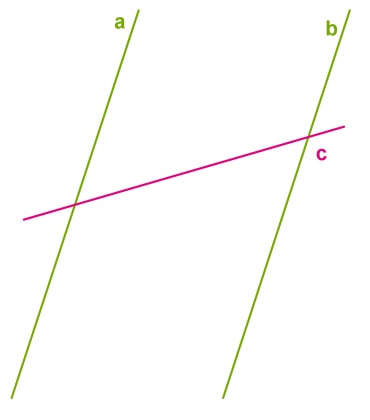
| 3. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. 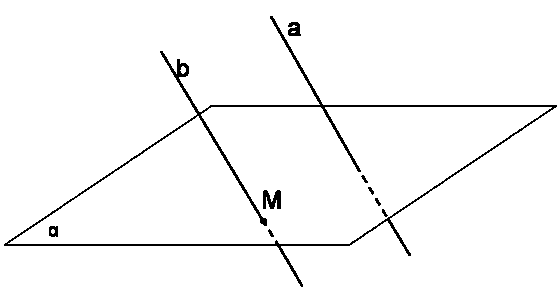
|
Первые уроки геометрии в 10 классе по темам: "Аксиомы стереометрии" и «Параллельность прямых и плоскостей» играют важную роль в развитии пространственных представлений, поэтому, важно: 1) использовать таблицы, рисунки, наглядные чертежи; 2) изготавливать модели прямых и плоскостей из картона, ниток, проволоки, спиц; 3) показывать как строятся изображения пространственных фигур на плоскости; 4) использовать современные компьютерные технологии при построении многогранников и их сечений. Таким образом, геометрия, соединяя в себе логику и воображение, дает метод научного познания мира.





 очка, прямая
очка, прямая
 очка, прямая, плоскость
очка, прямая, плоскость
 трезок, луч, угол, треугольник, многоугольник, окружность, круг ●
трезок, луч, угол, треугольник, многоугольник, окружность, круг ● ●
●