Гиперболические функции

Бюджетное муниципальное общеобразовательное учреждение

«Школа № 31»

Школьная Академия Наук «Созвездие»

СЕКЦИЯ

математики, информатики, физики

Доклад

На тему «Некоторые практические приложения гиперболических функций»

Выполнила учитель математики

Кряквина Лилия Низамитдиновна

г. Ростов-на-Дону

2019 г.

Оглавление

стр.

1. Введение………………………………………………………………3

2. Результаты исследования…………………………………………….5

3. Выводы………………………………………………………………...9

4. Приложение…………………………………………………………..10

5. Литература……………………………………………………………13

Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени. Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы¹.

Современная математика рассматривает гиперболические функции, как пары экспоненциальной функции, но Риккати исследовал их свойства, используя только геометрические свойства гиперболы х² — y² = 1 или 2xy = 1. Он использовал геометрические методы, хотя он был знаком с работами Эйлера, предшествовавших выходу книги Риккати.

Над гиперболическими функциями Риккати работал вместе с Джироламо Саладини. Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.

Цель данной работы – изучить гиперболические функции и их применение.

В задачи работы входит изучение следующих вопросов:

1. Раскрыть понятие о гиперболических функциях.

2. Изучить основные свойства и графики гиперболических функций.

3. Рассмотреть применение гиперболических синуса и косинуса при решении уравнения с параметром.

Актуальность темы заключается в том, что прикладной характер гиперболических функций достаточно широк (применение в физике, информатике, архитектуре).

Новизна темы базируется на оригинальном, нестандартном методе решения уравнения с параметром. Кроме того, в работе предоставлен материал, выходящий за рамки школьного курса.

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями².

Гиперболические функции задаются следующими формулами:

гиперболический синус:

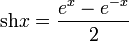
гиперболический косинус:

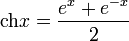
гиперболический тангенс:

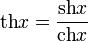
гиперболический котангенс:

,

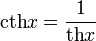Иногда также определяются гиперболические секанс и косеканс:

,

.

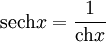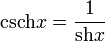Ввиду соотношения 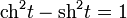гиперболические функции дают параметрическое представление гиперболы x₂ − y₂ = 1 ( 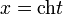, 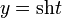). При этом аргумент t = 2S, где S — площадь криволинейного треугольника, взятая со знаком «+», если сектор лежит выше оси OX, и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.

Важные тождества

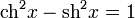
Чётность:

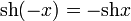
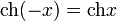
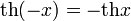
Формулы сложения:

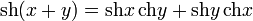
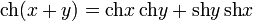
Формулы двойного угла:

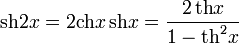
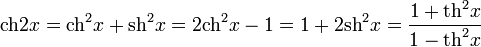
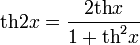
Формулы понижения степени

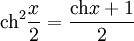
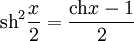
2. 3 Примеры применения гиперболических функций при решении задач

Задание Доказать тождество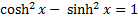
Доказательство По определению


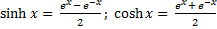
Подставим эти выражения в левую часть заданного равенства:







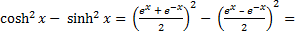
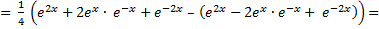
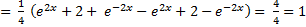
Что и требовалось доказать.

Задание Найти приближенное значение
Решение По определению , подставляем значение , получим


В последнее выражение подставим значение экспоненты :




Ответ

Пример использования гиперболических функций при решений уравнений с параметрами.

П ример 3

Найти корни уравнения .
Решение
Пусть , тогда ; , . Исходное уравнение равносильно уравнению
; ;
; .
Имеем = b; Введем переменную
Таким образом, получили .
Найдем дискриминант уравнения: .
Если
0.
При .

;
.
Ответ:

3. Выводы

Представленный в работе материал нетривиален и полезен для приложений. Выше рассмотренные гиперболические функции имеют большую практическую значимость, поскольку их использование является важным в физике, архитектуре, информатике. Гиперболические функции часто встречаются в теории относительности. Однородная веревка или цепочка, свободно подвешенная за свои концы, приобретает форму графика функции (в связи с чем график гиперболического косинуса иногда называют цепной линией). Это обстоятельство используется при проектировании арок, поскольку форма арки в виде перевёрнутой цепной линии наиболее удачно распределяет нагрузку. Гиперболический тангенс используют в качестве функции активации в нейронных сетях. Гиперболические функции используются при сжатии информации. Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций.

В работе показан оригинальный приём решения уравнения с параметром, позволяющий достаточно сложное уравнение свести к стандартному квадратному уравнению с параметром. Естественно, что это даёт хороший опыт работы с заданиями повышенного уровня сложности.

4. Приложения

Графики гиперболических функций даны на рис. 1.

Рисунок 1.

Гиперболические функции в компьютерных программах

Гиперболические функции представлены следующим набором:

sinh — гиперболический синус;

cosh — гиперболический косинус;

tanh — гиперболический тангенс;

sech — гиперболический секанс;

csch — гиперболический косеканс;

coth — гиперболический котангенс.

Примеры применения гиперболических функций представлены ниже:

На рис. 2 сверху представлены графики гиперболического синуса, косинуса и тангенса. По ним можно судить о поведении этих функций.

Рис. 2. Графики основных гиперболических и обратных гиперболических функций

5. Литература

1. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Наука, 2004.

2. Ильин В. А., Позняк Э. Г. Основы математического анализа: В 2-х ч. Часть I: Учеб. для вузов. - 7-е изд. - М.: ФИЗМАТЛИТ, 2004.

3. Казимиров Н.И. Математический анализ. Конспект лекций для специальности "Физика". - Петрозаводск, 2002.

4. Начало математического анализа: Учеб.-метод. пособие / Авт.-сост.: А.Я. Алеева, Ю.Ю. Громов, О.Г. Иванова, А.В. Лагутин. - Тамбов: Изд-во Тамб. гос. техн. ун-та, 2001

5. Стахов A.П. Обобщенные Золотые Сечения и новый подход к геометрическому определению числа // Украинский математический журнал, 2004, том 56, № 8.

6. Стахов А.П. Формула Кассини // М.: «Академия Тринитаризма», Эл № 77-6567, публ.12542, 01.11.2005.

7. Владимиров Ю.С. Метафизика. – M.: Бином, 2002.

8. Бугров Я. С., Никольский С. М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. — Москва: Наука, 1998г.

9. Шерватов В.Г. Гиперболические функции. Государственное издательство технико – теоретической литературы.М.2003г.

1 Начало математического анализа: Учеб.-метод. пособие / Авт.-сост.: А.Я. Алеева, Ю.Ю. Громов, О.Г. Иванова, А.В. Лагутин. - Тамбов: Изд-во Тамб. гос. техн. ун-та, 2001. С. 193.

2 Аксёнов А.П. Математический анализ. Интегралы, зависящие от параметра. Двойные интегралы. Криволинейные интегралы. Учебное пособие. - СПб.: Изд-во "НЕСТОР", 2000. С. 163.