Графические возможности среды программирования PASCALABC

Физико – математический факультет

Кафедра информатики и вычислительной техники

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

ГРАФИЧЕСКИЕ ВОЗМОЖНОСТИ СРЕДЫ ПРОГРАММИРОВАНИЯ PASCALABC

Автор работы: Е.С. Налейкина

_____________ ___________

Содержание

Введение 3

1Теоретические основы языка программирования Паскаль 5

1.1 Краткая история становления языка программирования Pascal 5

1.2 Основные понятия графики 7

1.3 Основные функции и процедуры работы с графикой в PascalABC 8

2 Создание графического проекта 13

2.1 Понятие «фрактал» 13

2.2 Построение фрактала «Дерево» и реализация треугольника 15

2.4 Создание анимированного изображения с помощью языка программирования PascalABC 20

Заключение 28

Список использованных источников 29

Введение

Курс языка программирования даёт учащимся очень важный в современных условиях блок знаний, навыков и умений, которые им могут пригодиться в жизни. Изучая программирование, ученики больше понимают сущность работы компьютеров, их возможности и границы их применения, помогает пройти все основные этапы решения некой творческой, точно сформулированной задачи. Всем учащимся, без исключения, это помогает развивать навыки мышления и решения задач. Без овладения решением задач трудно быть культурным человеком и вообще полноценным членом общества. Учащиеся разных возрастов получают уникальную возможность, поэтапно, соразмерно возрасту, развивать свои логико-алгоритмические способности в целом и творческие способности в области точных наук особенно. Иначе говоря, основы программирования являются не только наукой или учебной дисциплиной в её обычном понимании, но и средством развития личности, способностей детей, побуждает интеллектуальные задатки освоения других дисциплин. Методы, которые дети освоят на уроках программирования, обязательно будут использоваться позднее при решении самых различных «взрослых» жизненных и профессиональных задач. Возможно, это проявится не осознанно и через много лет после окончания школьного курса информатики, однако и ради этого стоит учить программированию. Как правило, ученикам нравится управлять работой компьютера при помощи собственных программ. Программирование для некоторых детей становится любимым занятием, как в школе, так и дома.

Тема курсовой работы выбрана не случайно, так как графика является довольно интересной областью программирования. Данная курсовая работа показывает, что можно создавать простые рисунки не только в графических программах, таких как Paint, Adobe Photoshop, Corel Draw, но и в среде языка программирования PascalАВС.

Объект исследования: язык программирования PascalABC.

Предмет исследования: программирование изображений на языке PascalABC.

Целью курсовой работы является разработка графического проекта в среде программирования PascalАВС.

Для достижения цели были поставлены следующие задачи:

• ознакомиться с историей становления языка программирования PascalАВС;

• изучить основные понятия графики, функции и процедуры работы с графикой PascalАВС;

• освоить навыки создания графических изображений в среде программирования PascalАВС;

• создать графическое изображение в среде программирования PascalАВС с использованием фракталов.

• создать анимированное графическое изображение в среде программирования PascalАВС.

Курсовая работа состоит из двух основных разделов:

• аналитическая часть;

• создание графического проекта.

В первом разделе описывается история языка PascalАВС, основные понятия графики, работа с графикой в PascalАВС, основные команды построения изображения, графические модули, дается основная структура программы. Во втором разделе описываются этапы создания фрактального дерева, дается краткое изложение основных элементов рисунка.

1Теоретические основы языка программирования Паскаль

1.1 Краткая история становления языка программирования Pascal

Pascal ABC разработан в 2002 году сотрудниками факультета математики, механики и компьютерных наук Южного федерального университета (Ростов-на-Дону, Россия) во главе с С.С. Михалковичем. Целью авторов было создание обучающей среды программирования, более современной, чем Borland Pascal и Turbo Pascal, более простой для изучения, чем Borland Delphi, но в то же время близкой к стандартным компиляторам языка [2, c.180].

Система Pascal ABC основана на языке Delphi Pascal и призвана осуществить постепенный переход от простейших программ к модульному, объектно-ориентированному, событийному и компонентному программированию. Некоторые языковые конструкции в Pascal ABC допускают, наряду с основным, упрощенное использование, что позволяет использовать их на ранних этапах обучения. Например, в модулях может отсутствовать разделение на секцию интерфейса и секцию реализации. В этом случае модули устроены практически так же, как и основная программа, что позволяет приступить к их изучению параллельно с темой «Процедуры и функции». Тела методов можно определять непосредственно внутри классов (в стиле Java и C#), что позволяет создавать классы практически сразу после изучения записей, процедур и функций .

Ряд модулей системы программирования Pascal ABC специально создавался для учебных целей [2, c.180]:

• Модуль растровой графики GraphABC обходится без объектов, хотя его возможности практически совпадают с графическими возможностями Borland Delphi. Он доступен в несобытийных программах и позволяет легко создавать анимацию без мерцания.

• Модуль Events позволяет создавать простейшие событийные программы без использования объектов (события представляют собой обычные процедурные переменные).

• Модули Timers и Sounds позволяют создавать таймеры и звуки, которые также реализованы в процедурном стиле. Эти модули можно использовать даже в консольных программах.

• Модуль контейнерных классов Containers позволяет работать с основными структурами данных (динамические массивы, стеки, очереди, множества), реализованными в виде классов.

• Модуль векторной графики ABCObjects предназначен для быстрого изучения основ объектно-ориентированного программирования, а также позволяет создавать достаточно сложные игровые и обучающие программы.

• Модуль визуальных компонентов VCL позволяет создавать событийные приложения с главной формой в стиле Delphi. Классы VCL немного упрощены по сравнению с аналогичными классами Delphi. Имеется редактор форм и инспектор объектов. Технология восстановления формы по коду программы позволяет обойтись для приложения с главной формой одним файлом (!).

В языке Pascal ABC имеются арифметические операции с типизированными указателями (в стиле языка C), а также тип complex, предназначенный для работы с комплексными числами [2, c.181].

Компилятор Pascal ABC является компилятором переднего плана (front-end). Это означает, что он не генерирует исполняемый код в виде .exe-файла, а создает в результате компиляции дерево программы в памяти, которое затем выполняется с помощью встроенного интерпретатора. В итоге скорость работы программы примерно в 20 раз медленнее скорости работы этой же программы, откомпилированной в среде Borland Pascal, и в 50 раз медленнее этой программы, откомпилированной в среде Borland Delphi.

В системе Pascal ABC ученик может выполнять так называемые проверяемые задания, обеспечивающие постановку задачи со случайными исходными данными, контроль операций ввода-вывода, проверку правильности решения, а также ведение протокола решения задач [2, c.181].

1.2 Основные понятия графики

Экраны цветных мониторов состоят из прямоугольной решётки точек(пикселей),светящихся разным цветом. Каждый цветной пиксель образован тремя более мелкими по площади участками красного, зелёного и синего цветов. При свечении этих участков с разной интенсивностью цвета смешиваются, создавая элементы изображения различных оттенков и яркости. Важной характеристикой растра является его расширение. Расширение экрана-это количество точек (пикселей) на единицу длины. Чем это число выше, тем более мелкими являются сами пиксели, и, соответственно, более плотно они располагаются на плоскости, что и приводит к тому, что мы воспринимаем их как единое, цельное изображение [5, c.173]. Из года в год разрешающая способность принтеров, мониторов, сканеров и .т.п. растёт. Для использования графических возможностей языка Паскаль необходимо в блоке описания uses подключить графический модуль Graph .Модуль содержит набор графических функций и процедур, основные из них которые рассмотрены ниже. Положение каждой точки изображения задано координатами Х и У. Координаты – целые числа, они задают номера колонки и строки и не зависят от физического размера экрана. Оси координат направлены следующим образом: горизонтальная ось Х направлена слева направо; вертикальная ось У направлена сверху вниз; верхний левый угол имеет координаты(0, 0) (рис. 1.1).

Рисунок 1.1 – Направление оси координат

Очевидно, что запись изображения требует хранения информации о положении множества точек, для каждой из которых должен быть задан цвет. Цветное изображение получается смешиванием трех основных цветов - красного, зеленого и синего. Такая модель представления цвета называется моделью RGB (Red – Green – Blue). Управляя интенсивностью компонентов, можно получить различные оттенки и степени интенсивности цвета. В частности, для получения градаций серого надо взять интенсивности трех основных цветов равными друг другу. Стандартный модуль GraphABC системы PascalABC содержит типы, константы, переменные, процедуры и функции, позволяющие создавать изображения в специальном графическом окне [5, c.174].

1.3 Основные функции и процедуры работы с графикой в PascalABC

Для рисования в Pascal ABC необходимо запустить специальный модуль GraphABC, использование специальных функций и процедур помогут нарисовать точку, отрезок, окружность, прямоугольник и другие фигуры [5, c.180]:

SetPixel (x,y,color) – закрашивает один пиксел с координатами (x,y) цветом color.

LineTo(x,y) – рисует отрезок от текущего положения пера до точки (x,y); координаты пера при этом также становятся равными (x,y).

Line(x1,y1,x2,y2) – рисует отрезок с началом в точке (x1,y1) и концом в точке (x2,y2).

SetPenColor(color) – устанавливает цвет пера, задаваемый параметром color.

SetPenWidth(n) – устанавливает ширину (толщину) пера, равную n пикселям.

Rectangle(x1,y1,x2,y2) – рисует прямоугольник, заданный координатами противоположных вершин (x1,y1) и (x2,y2).

FloodFill(x,y,color) – заливает область одного цвета цветом color, начиная с точки (x,y).

SetBrushColor(color) – устанавливает цвет кисти. Заливка кистью распространяется на замкнутый контур, описание которого следует за процедурой установки цвета кисти.

Ellipse(x1,y1,x2,y2) – рисует эллипс, заданный своим описанным прямоугольником с координатами противоположных вершин (x1,y1) и (x2,y2).

Circle(x,y,r) – рисует окружность с центром в точке (x,y) и радиусом r.

Arc(x,y,r,a1,a2) – рисует дугу окружности с центром в точке (x,y) и радиусом r, заключенной между двумя лучами, образующими углы a1 и a2 с осью OX (a1 и a2 – вещественные, задаются в градусах и отсчитываются против часовой стрелки).

Цвета в PascalABC: clPurple фиолетовый, clWhite белый, clMaroon темно-красный, clRed красный, clNavy темно-синий, clGreen зеленый, clBrown коричневый, clBlue синий, clSkyBlue голубой, clYellow желтый, clCream кремовый, clAqua бирюзовый, clOlive оливковый, clFuchsia сиреневый, clTeal сине-зеленый, clGray темно-серый, clLime ярко-зеленый, clMoneyGreen цвет зеленых денег, clLtGray светло-серый, clDkGray темно-серый, clMedGray серый, clSilver серебряный [5, c.180].

Функции для работы с цветом

Тип цвета Color является синонимом System.Drawing.Color.

function RGB(r,g,b: byte): Color; Возвращает цвет, который содержит красную (r), зеленую (g) и синюю (b) составляющие (r,g и b – в диапазоне от 0 до 255).

function ARGB(a,r,g,b: byte): Color; Возвращает цвет, который содержит красную (r), зеленую (g) и синюю (b) составляющие и прозрачность (a) (a,r,g,b – в диапазоне от 0 до 255).

function RedColor(r: byte): Color; Возвращает красный цвет с интенсивностью r (r – в диапазоне от 0 до 255).

function GreenColor(g: byte): Color; Возвращает зеленый цвет с интенсивностью g (g – в диапазоне от 0 до 255).

function BlueColor(b: byte): Color; Возвращает синий цвет с интенсивностью b (b – в диапазоне от 0 до 255)clRandom: Color; Возвращает случайный цвет.

function GetRed(c: Color): integer;Возвращает красную составляющую цветаGetGreen(c: Color): integer; Возвращает зеленую составляющую цвета.

function GetBlue(c: Color): integer; Возвращает синюю составляющую цвета.

Свойства: property Width: integer; Ширина рисунка. Height: integer; Высота рисунка.Transparent: boolean; Прозрачность рисунка. Если Transparent=True, то при выводе рисунка его фон не отображается. Фоновым считается цвет левого нижнего пиксела рисунка.NeedDestroy: boolean; Определяет, должен ли рисунок разрушаться при вызове деструктора и метода Load. NeedDestroy обычно устанавливается в False, если несколько объектов классаPicture разделяют один рисунок [5, c.183].

Методы:

procedure Load(fname: string);

Загружает рисунок из файла с именем fname. Если NeedDestroy установлено в True, то рисунок, находившийся ранее в объекте Picture, разрушается. Рисунок с именем fname ищется вначале в текущем каталоге, а затем в подкаталоге Media\Images\ каталога программы PascalABC.exe.Save(fname: string);

Сохраняет рисунок в файле с именем fname. Формат рисунка устанавливается расширением имени файла. Допустимые расширения: .bmp, .gif, .jpg, .png.Handle: integer;

Возвращает описатель рисунка: procedure Draw(x,y: integer);

Выводит рисунок в позицию (x,y) графического окна: procedure Draw (x,y,w,h: integer);

Выводит рисунок в позицию (x,y) графического окна, масштабируя его к размеру (w,h). Если w

Выводит часть рисунка, заключенную в прямоугольнике r, в позицию (x,y) графического окна.Draw(x,y,w,h: integer; src: Rect);

Выводит часть рисунка, заключенную в прямоугольнике r, в позицию (x,y) графического окна, масштабируя ее к размеру (w,h): procedure CopyRect(dest: Rect; p: Picture; src: Rect);

Копирует в прямоугольник dest текущего рисунка часть рисунка p, заключенную в прямоугольнике src.FlipHorizontal; Зеркально отображает картинку относительно горизонтальной оси симметрии.FlipVertical;Зеркально отображает картинку относительно вертикальной оси симметрии [5, c.184].

Рисование графических объектов

Рисование графических объектов осуществляется пером и кистью. Линии, ограничивающие объекты, рисуются пером. Действия с перомтекущая координата X ператекущая координата Y пераустановка цвета ператекущий цвет пераперемещение перарисование отрезка от текущего положения пераустановка ширины ператекущая ширина пераустановка стиля ператекущий стиль пераустановка режима ператекущий режим пера [5, c.185].

Режим пера определяет, как цвет пера взаимодействует с цветом поверхности. В GraphABC два режима пера:- обычный режим: при рисовании цвет поверхности заменяется цветом пера; 25- режим инвертирования: при рисовании цвет поверхности инвертируется (становится негативным), а цвет пера при этом игнорируется.

Пример 1(рис.1.2):

crt,GraphABC;,x1,y,y1:longint;:=150;(150,10,125,85);

{строим звезду}(125,85,150,110);

x1:=150 to 175 do(x,10,x1,110-(x1-150));(250,110,175,85);

y1:=110 to 135 do(250,110,150+(y1-110),

y(1);(150,220,175,135); x1:=150 downto 125 do(150,220,x1,110-(x1-150));(40,110,125,135);

y1:=110 downto 85 do(40,110,150+(y1-110),y1);

{line(90,50,210,170);(210,50,90,170); дополнительное построение}(210,50,165,55);

line(210,50,205,95);(90,170,95,125);(90,170,135,165);(90,50,95,95);(90,50,135,55);(210,170,165,165);

line(210,170,205,125);

end.

Рисунок 1.2 – Пример графического изображения

Пример 2 (рис. 1.3)

graphABC;=Pi*0.2;DrawStar(x,y,size:integer);

{x,y – координаты центра и size – радиус снежинки}

i,j,newsize, xnew,ynew:integer;size

for i:=0 to 9 do {первый цикл – по количеству направляющих снежинки}:=size;j:=1 to 8 do {второй цикл -рисование 8-ми подуровней снежинки}

begin:=x+round(newsize*cos(i*step));:=y+round(newsize*sin(i*step));(xnew,ynew,newsize div 5);:=newsize*2 div 3;;;;{конец процедуры}{Главная}

DrawStar(320,240,160);.

Рисунок 1.3 – Пример графического изображения «Снежинка»

2 Создание графического проекта

2.1 Понятие «фрактал»

Роль фракталов в компьютерной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные [13, c. 320].

Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию обо всем фрактале.

Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому».

Геометрические фракталы

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе [13, c. 320]. В результате бесконечного повторения этой процедуры, получается геометрический фрактал (рис. 2.1).

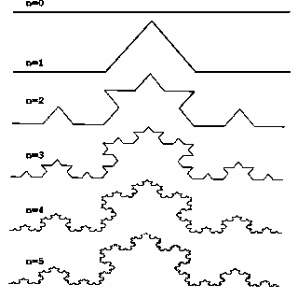
Рисунок 2.1 – Геометрический фрактал

Алгебраические фракталы

Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д. [13, c. 321]

Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят – аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры (рис. 2.2).

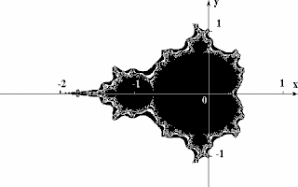
Рисунок 2.2 – Алгебраический фрактал

Стохастические фракталы

Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные – несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

Существуют и другие классификации фракталов, например деление фракталов на детерминированные (алгебраические и геометрические) и недетерминированные (стохастические) [13, c. 322].

2.2 Построение фрактала «Дерево» и реализация треугольника

Треугольник

Отображается в виде треугольника, из четырех секций, каждый треугольник имеет половину ширины и высоты оригинала (рис. 2.3). Центральный треугольник инвертируется и может рассматриваться как отверстие в изображении. Каждый из трех внешних треугольников являются уменьшенной версией целого рисунка с собственными центральными отверстиями. Такая схема повторяется бесконечно.

Рисунок 2.3 – Реализация треугольника

Алгоритм построения

Существуют различные методы построения треугольника .Одним из них является использование теории хаоса с тремя аттракторами, расположенными на трех вершинах равностороннего треугольника. При переходе с текущей позиции в направлении аттрактора пройденное расстояние всегда составляет расстояние между текущей точкой и выбранной вершиной.

Рассмотрим шаги для построения фрактала:

1. Определить три точки.

2. Выбрать стартовую позицию.

3. Случайно выбрать один из трех аттракторов.

4. Переместить текущую позицию на половину в направлении позиции аттрактора и нарисовать точку.

5. Вернуться к шагу 3.

Рисование треугольника

Нам понадобиться три метода. Первый для генерации псевдо – случайных чисел, которые будут использоваться для определения направления во время каждой итерации. Во - вторых, нам необходимо сохранить три позиции равностороннего треугольника, для этого будем использовать структуру Point. Наконец, еще одна структура Point понадобиться для хранения текущей позиции. Объявим три переменные:randomiser = new Random();Point[] points; private Point currentLocation;

Размер треугольника должен быть, как можно больше, чтобы рассмотреть детали. Чтобы определить наибольший возможный размер, мы должны рассматривать соотношение между высотой и шириной любого равностороннего треугольника. Если предположить, что основание треугольника выравнивается по горизонтали, ширина будет такая же, как длина одной из сторон. Высота будет иметь ширину, умноженная на половину квадратного корня из трех. Добавим метод, который рассчитает соотношение:

private double HeightWidthRatio()

{Math.Sqrt(3) / 2}

Следующий метод вычисляет размер треугольника, чтобы поместить на форме:

private int SideLength()

{height = (int)Math.Min(

(double)ClientSize.Width, ClientSize.Height / HeightWidthRatio());

// отнимаем 2 чтобы треугольник не примыкал к краям.(int)height – 2;}

Следующий метод будет вычислять позиции каждого из трех аттракторов, каждый будет расположен в вершине треугольника. Эти значения будут основаны на размере треугольника и медиане клиентской области формы.

void SetPointLocations(int sideLength)

{

Point midPoint = new Point(ClientSize.Width / 2, ClientSize.Height / 2);= new Point[3];[0] = new Point(midPoint.X

, midPoint.Y - (int)(sideLength * HeightWidthRatio() / 2));[1] = new Point(midPoint.X - sideLength / 2

, midPoint.Y + (int)(sideLength * HeightWidthRatio() / 2));[2] = new Point(midPoint.X + sideLength / 2

, midPoint.Y + (int)(sideLength * HeightWidthRatio() / 2));

}

Следующей задачей является создание метода (точнее двух) для размещения точек.

void PlotPointLocations(Graphics g)

{(Point p in _points)

{(p, g);

}

}void PlotPoint(Point p, Graphics g)

{b = new SolidBrush(Color.Black);.FillRectangle(b, p.X, p.Y, 1, 1);

}

Теперь напишем методы, которые используются в цикле алгоритмом для рисования фрактала. Метод DrawNextPoint будет контролировать этот процесс вызывая «MoveTowardsRandomPoint», за которым следует вызов PlotPoint, чтобы поставить точку в текущей позиции. Наконец, вызывается метод Application.DoEvents для обновления формы.

Метод MoveTowardsRandomPoint выбирает одну из трех вершин используя наш объект randomizer.Он как раз и вычисляет половину расстояния между текущей позицией и выбранным аттрактором:

void DrawNextPoint(Graphics g)

{

MoveTowardsRandomPoint();(currentLocation, g);.DoEvents();

}

private void MoveTowardsRandomPoint()

{moveTowards = randomiser.Next(0,3);.X = (currentLocation.X + points[moveTowards].X) / 2;.Y = (currentLocation.Y + points[moveTowards].Y) / 2;

}

Метод для вызова всего что мы написали:

void DrawTriangle(Graphics g)

{sideLength = SideLength();(sideLength);(g);= new Point(points[0].X, points[0].Y);

while (working)

{(g);

}

}

Поместим две кнопки для Старт и Стоп на форму и в обработчике события Click напишем:

private void StopButton_Click(object sender, EventArgs e)

{.Enabled = true;.Enabled = false;= false;

}

private void StartButton_Click(object sender, EventArgs e)

{.Enabled = false;.Enabled = true;g = CreateGraphics();.Clear(Color.White);= true;(g);

}

Построения фрактала «Дерево»

Алгоритм построения «Веточки» .

Первый отрезок рисуется под произвольным углом к оси Ох, из конца данного отрезка рисуется пара отрезков, направленных в противоположные стороны от направления первого отрезка под одинаковым величиной 30 градусов. Далее рисунок повторяется с каждым из вновь построенных отрезков с уменьшением длины отрезка примерно в полтора раза.

Вложенность такого рекурсивного рисунка очевидно, не менее семи.

Рекурсивная функция имеет 4 параметра: координаты начала отрезка, его длину и угол, под некоторым рисуется отрезок к ос Ох.

Алгоритм построения состоит из следующих шагов:

1. Нарисовать отрезок.

2. Вызвать рекурсивную процедуру, рисующую левую ветку, с новыми параметрами (за координаты начала отрезка взять только что вычисленные координаты конца отрезка, за длину - длину, уменьшенную в полтора раза, за угол, уменьшенный на 30 градусов.

3. Вызвать рекурсивную процедуру, рисующую правую ветку (параметры такие же, как в пункте 2, за исключением угла - новый угол увеличивается на 30 градусов относительно первоначального угла).

4. Выход из процедуры осуществляется, когда длина ветки становится очень малой (около 2 пикселей).

В программе имеется лишь одно обращение к процедуре со следующими параметрами: координаты начала самого первого отрезка, первоначальная длина отрезка, первоначальная длина отрезка и произвольный угол наклона.

Программа «Ветка дерева» на языке PascalABC (рис.2.4).

uses GraphABC;=Pi/180; deltaangle=30*radian;Ris(x,y: integer; len, angle: real);, xnew, ynew:integer;

if lenthen exit;

{Выход из рекурсии при длине ветки меньше 1 пиксела}

if len

{Листья - жёлтым цветом, ствол белым}

xnew:=x+round(Len*cos(angle));

{координаты конца ветки}:=y+ round(len*sin(angle));(color); Line(x,y,xnew,ynew);

{Рисуем ветку}(xnew, ynew, len*0.65, angle-deltaangle);

{Рисуем левую подветку}(xnew, ynew, len*0.65, angle+deltaangle);

{Рисуем правую подветку};(100,400,160,–40*radian);.

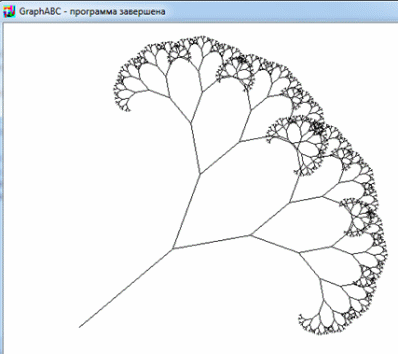
Рисунок 2.4 – «Ветка дерева»

2.4 Создание анимированного изображения с помощью языка программирования PascalABC

Для работы с графикой в PascalABC используется модуль GraphABC. Для его подключения используется следующий код:

uses GraphABC; begin ... end.

Система координат в Паскале соответствует экранной системе координат и выглядит следующим образом (рис. 2.5):

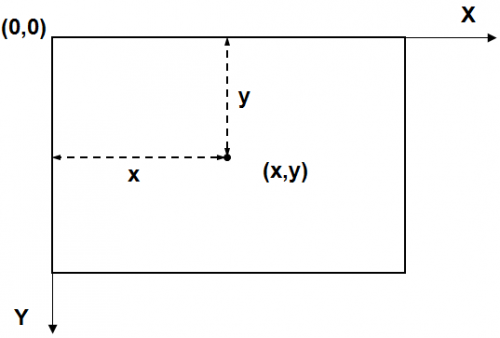
Рисунок 2.5 – Система координат

Управление цветом

Для того, чтобы использовать цвет, необходимо применить этот цвет к инструменту перо:

• SetPenColor(color) – устанавливает цвет пера, задаваемый параметром color;

• setBrushColor(color) – устанавливает цвет кисти, задаваемый параметром color;

• либо для палитры RGB: SetPenColor(rgb(0-256, 0-256, 0-256));

• или использовать для заливки:

• FloodFill(x,y,color) – заливает область одного цвета цветом color, начиная с точки (x,y).

После чего можно использовать процедуры для рисования геометрических фигур.

Цвета в pascal abc:

clBlack – черный

clPurple – фиолетовый

clWhite – белый

clMaroon – темно-красный

clRed – красный

clNavy – темно-синий

clGreen – зеленый

clBrown – коричневый

clBlue – синий

clSkyBlue – голубой

clYellow – желтый

clCream – кремовый

clAqua – бирюзовый

clOlive – оливковый

clFuchsia – сиреневый

clTeal – сине-зеленый

clGray – темно-серый

clLime – ярко-зеленый

clMoneyGreen – цвет зеленых денег

clLtGray – светло-серый

clDkGray – темно-серый

clMedGray – серый

clSilver – серебряный

Точки, отрезки и ломаные

Для отображения точки в паскале используется процедура:

SetPixel(x,y,color) – Закрашивает один пиксел с координатами (x,y) цветом color.

uses GraphABC; begin SetPixel(300,200,clred); end.

Для рисования линии используется:

Line(x1,y1,x2,y2) — рисует отрезок с началом в точке (x1,y1) и концом в точке (x2,y2) (рис. 2.6).

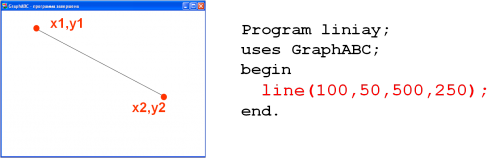
Рисунок 2.6 – Отрезок

uses GraphABC; begin SetPenColor(clgreen); line(100,50,500,250); end.

Ломаные можно рисовать с помощью процедур MoveTo (x1, y1) и LineTo (x2, y2) (рис. 2.7).

Процедуры работают в паре: MoveTo передвигает курсор в определенную точку, а процедура LineTo рисует линию с этой точки до точки, определенной параметром данной процедуры.

Рисунок 2.7 – Ломаная

Окружность, эллипс, дуга, сектор

Процедура Circle ( x, y: integer; r: word) вычерчивает окружность радиуса r с центром в точке с координатами ( x, y).

Процедура Arc ( x, y, ugol begin, ugol end, r: integer) вычерчивает дугу окружности радиуса r с центром в точке с координатами ( x, y). Параметры ugol_ begin и ugol_ end задают угловые координаты начала и конца дуги. Отсчет углов ведется против часовой стрелки. Значения угловых координат задается в градусах.

Процедура Ellips ( x, y: integer; ugol begin, ugol end, rx, ry: word) вычерчивает эллипс или дугу эллипса с центром в точке с координатами ( x, y). Параметры ugol_ begin и ugol_ end задают угловые координаты начала и конца дуги. Параметры rx и ry определяют горизонтальный и вертикальный радиусы эллипса.

Процедура PieSlice ( x, y: integer; ugol begin, ugol end, r: word) вычерчивает сектор окружности радиуса r с центром в точке с координатами ( x, y). Параметры ugol begin и ugol end задают угловые координаты начала и конца сектора.

Сектор может быть закрашен в соответствии со стилем, заданным процедурой SetFillStyle (о ней чуть позже).

Процедура Sector ( x, y: integer; ugol begin, ugol end, rx, ry: word) вычерчивает сектор эллипса с центром в точке с координатами ( x, y) и горизонтальным радиусом rx, вертикальным - ry. Параметры ugol begin и ugol end задают угловые координаты начала и конца сектора.

Сектор может быть закрашен в соответствии со стилем, заданным процедурой SetFillStyle.

Создание анимированного изображения «Домик» (рис. 2.8).

Анимацию мы можем создать с помощью цикла (повторения действий). В нашей программе цикл повторяется в строке.

Оператор цикла задает повторное выполнение определенных операторов. Для реализации циклов в Паскале предусмотрены три различных структурных оператора: WHILE, REPEAT, FOR. Первые два используются, если число повторений (итераций) заранее не определено, но известно условие завершения цикла. Оператор FOR применяется тогда, когда число повторений тела цикла известно.

Код программы

program grafika_cikl_1;

uses graphABC;

var x,y:word;

begin

x:=0;

while x600 do begin

setWindowSize(600,600);

rectangle(x+20,40,x+100,100);

line(x+20,40,x+60,10);

line(x+100,40,x+60,10);

ellipse(x+50,20,x+70,30);

rectangle(x+30,45,x+60,80);

line(x+30,55,x+60,55);

line(x+45,55,x+45,80);

line(x+70,16,x+70,5);

line(x+70,5,x+64,5);

line(x+64,5,x+64,12);

ellipse(x+72,2,x+82,9);

ellipse(x+85,2,x+94,11);

rectangle(x+70,55,x+90,95);

FloodFill(x+77,6,clGray);

FloodFill(x+90,7,clGray);

FloodFill(x+67,6,clBlack);

FloodFill(x+67,18,clBrown);

FloodFill(x+60,25,clYellow);

FloodFill(x+60,42,clNavy);

FloodFill(x+88,60,clGreen);

FloodFill(x+35,57,clYellow);

FloodFill(x+56,57,clYellow);

FloodFill(x+56,46,clYellow);

x:=x+120;

end;

end.

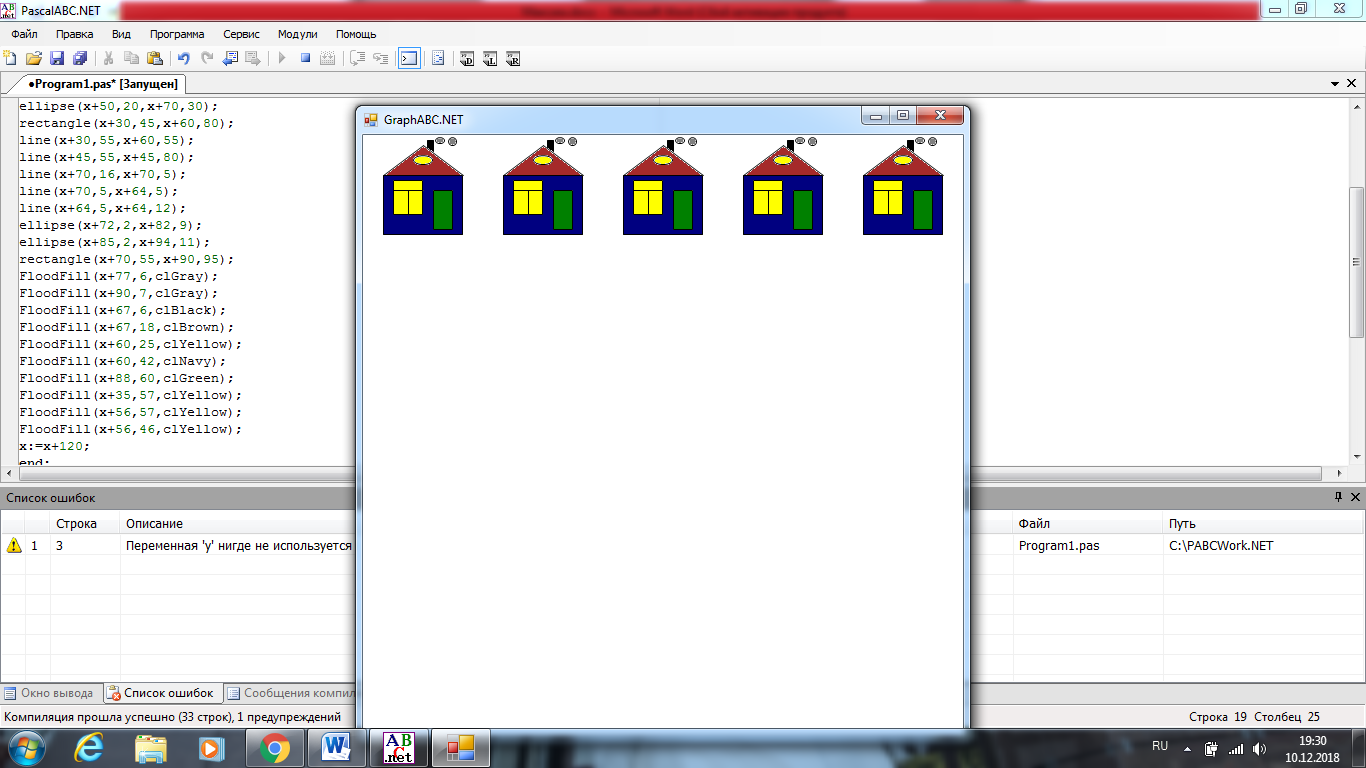
Рисунок 2.8 – Графическое изображение «Домик»

Заключение

Целью курсовой работы являлась разработка графического проекта в среде программирования PascalАВС.

Для достижение цели были решены следующие задачи:

• ознакомились с историей становления языка программирования PascalАВС;

• изучили основные понятия графики, функции и процедуры работы с графикой PascalАВС;

• освоили навыки создания графических изображений в среде программирования PascalАВС;

• создали анимированное графическое изображение в среде программирования PascalАВС.

• создали графическое изображение в среде программирования PascalАВС с использованием фракталов.

Полученные при исследовании знания и навыки будут полезны нам при дальнейшей работе в PascalАВС, а также при работе с другими языками программирования.

Список использованных источников

1. PascalABC: официальный сайт. [Электронный ресурс]. Режим доступа: http://pascalabc.net/

2. Абрамов, В. Г. Введение в язык паскаль / В.Г. Абрамов, Н.П. Трифонов, Г.Н. Трифонова. – М.: Наука, 2013. – 320 c.

3. Алкок, Д. Язык Паскаль в иллюстрациях / Д. Алкок. – М.: БХВ-Петербург, 2012. – 544 c.

4. Андреева, Т. А. Программирование на языке Pascal / Т.А. Андреева. – М.: Интернет-университет информационных технологий, Бином. Лаборатория знаний, 2013. – 240 c.

5. Арсак, Ж. Программирование игр и головоломок / Ж. Арсак. – М.: Главная редакция физико-математической литературы издательства «Наука», 2016. – 224 c.

6. Гильберт, Д. Основы теоретической логики / Д. Гильберт. – М.: МГТУ, 2007. – 215 c.

7. Грызлов, В. И. Турбо Паскаль 7.0 / В.И. Грызлов, Т.П. Грызлова. – М.: ДМК, 2016. – 416 c.

8. Гудман,С, Введение в разработку и анализ алгоритмов / С. Гудман. – М.: Юниор, 2011. – 216 c.

9. Епанешников, А. М. Программирование в среде PascalABC / А. М. Епанешников, В.А. Епанешников. – М.: Диалог-Мифи, 2011. – 368 c.

10. Зеленяк, О. П. Современный задачник по PascalABC / О.П. Зеленяк. – М.: ДМК Пресс, 2014. – 312 c.

11. Игошин, В. И. Задачи и упражнения по математической логике и теории алгоритмов: учеб. пособие для студ. высш. учеб. Заведений / В. И. Игошин. – М.: Академия, 2017. – 304 с.

12. Игошин, В. И. Математическая логика и теория алгоритмов / В. И. Игошин. – М.: Академия, 2008. – 448 с.

13. Йенсен, К. Паскаль: руководство для пользователя / К. Йенсен. – М.: БХВ-Петербург, 2010. – 244 c.

14. Касторнова, В. А. Структуры данных и алгоритмы их обработки на языке программирования Паскаль / В. А. Касторнова. – М.: БХВ-Петербург, 2016. – 304 c.

15. Кашаев, С. М. Паскаль для школьников. Подготовка к ЕГЭ (+ CD-ROM) / С.М. Кашаев, Л.В. Шерстнева. – М.: БХВ-Петербург, 2011. – 336 c.

16. Кетков, А. Практика программирования Бейсик, Си, Паскаль / А. Кетков, Ю. Кетков. – М.: БХВ-Петербург, 2011. – 480 c.

17. Кетков, Александр Практика программирования: Бейсик, Си, Паскаль. Самоучитель (+ дискета) / Александр Кетков , Юлий Кетков. – М.: БХВ-Петербург, 2013. – 480 c.

18. Кетков, Ю. Л. Свободное программное обеспечение. FREE PASCAL для студентов и школьников (+ CD) / Ю. Л. Кетков, А. Ю. Кетков. – М.: БХВ-Петербург, 2011. – 376 c.

19. Кетков, Ю. Л. Свободное программное обеспечение. FREE PASCAL для студентов и школьников / Ю. Л. Кетков, А. Ю. Кетков. – М.: БХВ-Петербург, 2011. – 384 c.

20. Климова, Л. М. PascalABC Практическое программирование. Решение типовых задач / Л. М. Климова. – М.: КУДИЦ-Образ, 2014. – 528 c.

21. Кореневская, О. В. PascalABC / О. В. Кореневская. – М.: НТ Пресс, 2014. – 144 c.

22. Культин, Н. PascalABC в задачах и примерах / Н. Культин. – М.: БХВ-Петербург, 2012. – 256 c.

23. Культин, Н. Программирование в PascalABC и Delphi (+ CD-ROM) / Н. Культин. – М.: БХВ-Петербург, 2012. – 390 c.

24. Культин, Н. Программирование в PascalABC и Delphi / Н. Культин. – М.: БХВ-Петербург, 2011. – 400 c.

25. Лингер, Р. Теория и практика структурного программирования / Р. Лингер. – М.: БХВ-Петербург, 2012. – 315 c.

26. Малыхина, М. П. Программирование на языке высокого уровня PascalABC / М.П. Малыхина. – М.: БХВ-Петербург, 2012. – 544 c.

27. Мейер, Б. Методы программирования / Б. Мейер. – М.: БХВ-Петербург, 2014. – 328 c.

28. Моргун, А. Н. Решение задач средствами языка PascalABC / А. Н. Моргун. – М.: Юниор, 2011. – 216 c.

29. Перминов, О. Н. Язык программирования Паскаль. Справочник / О. Н. Перминов. – М.: Радио и связь, 2015. – 128 c.

30. Фаронов, В. В. Турбо Паскаль. Книга 1. Основы Турбо Паскаля / В. В. Фараонов. – М.: БХВ-Петербург, 2012. – 412 c.