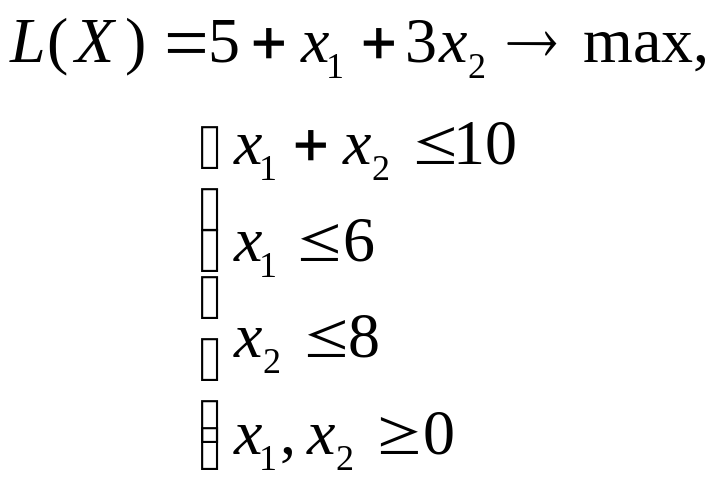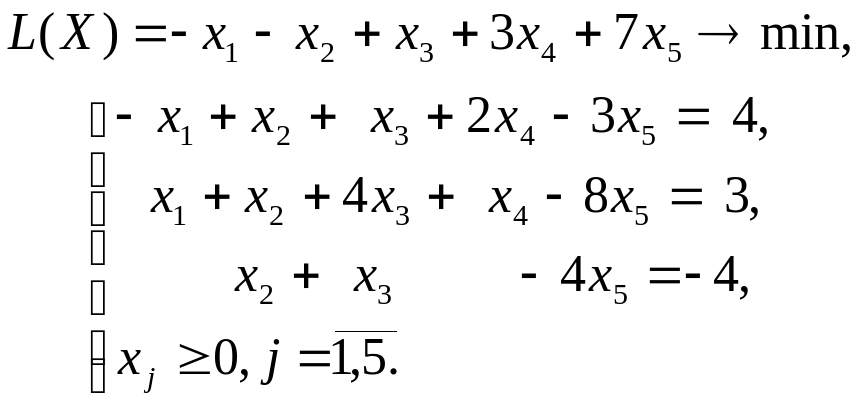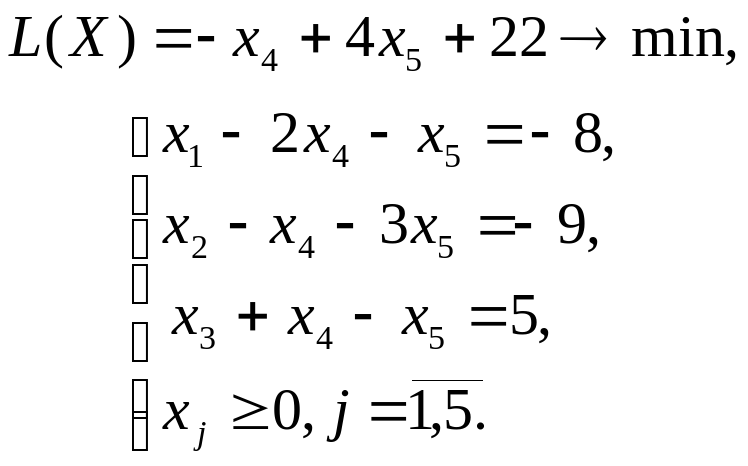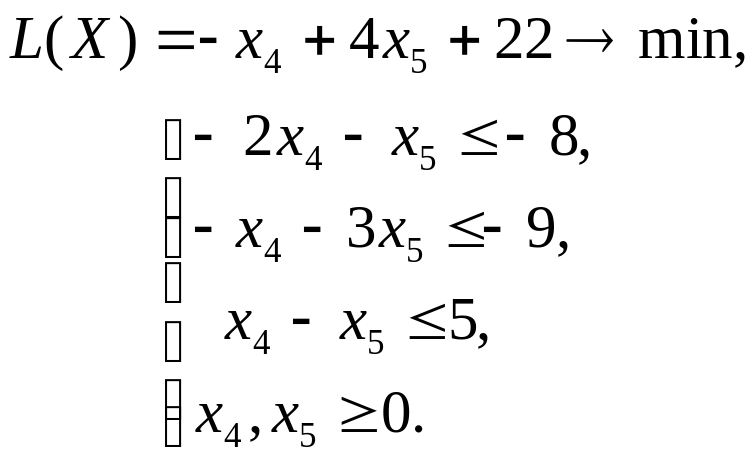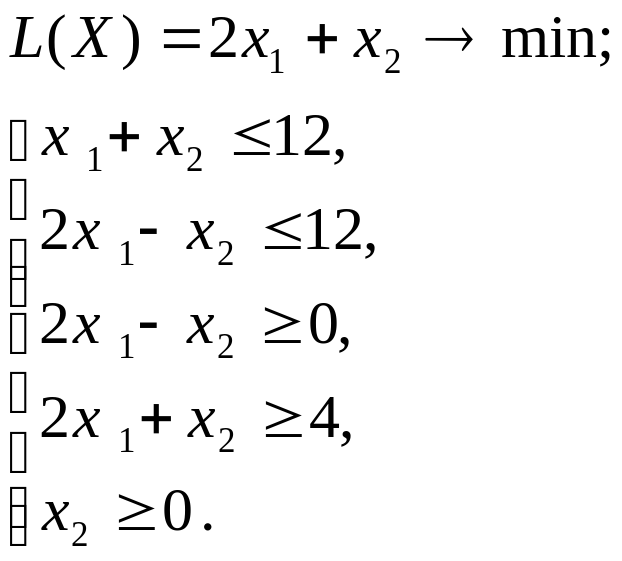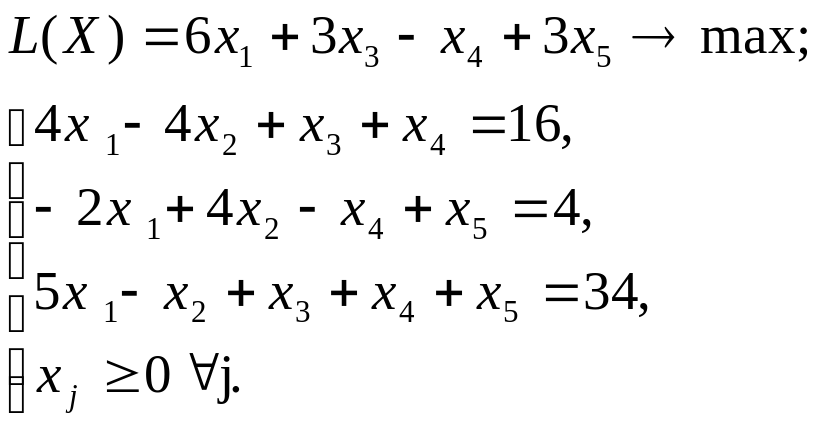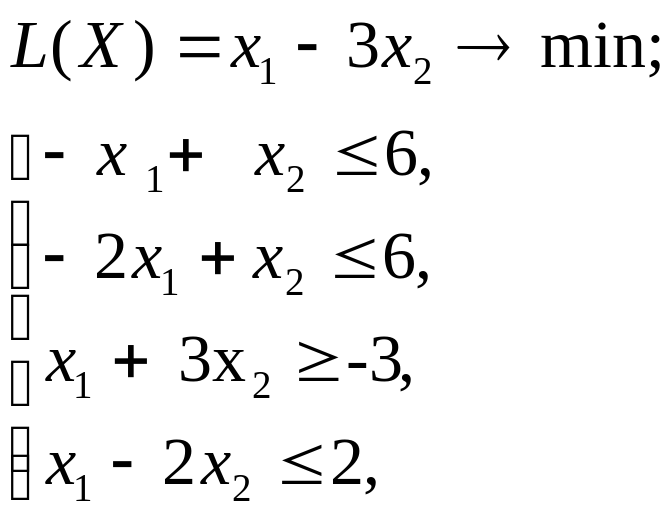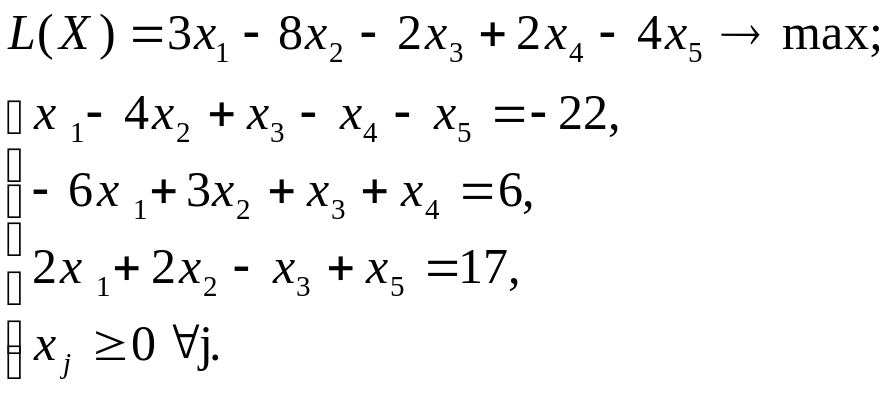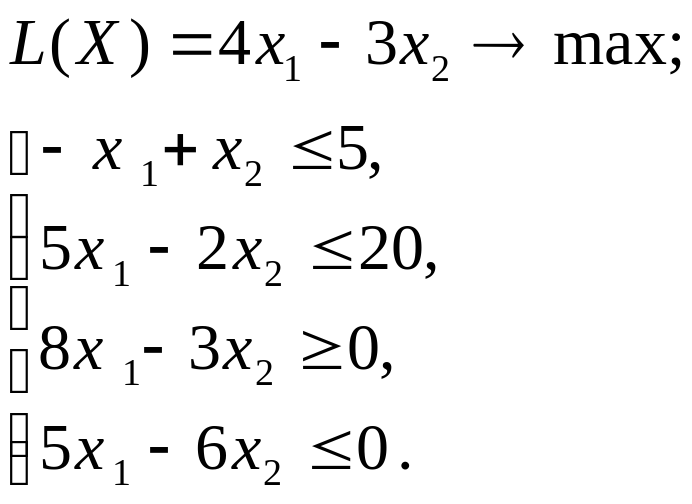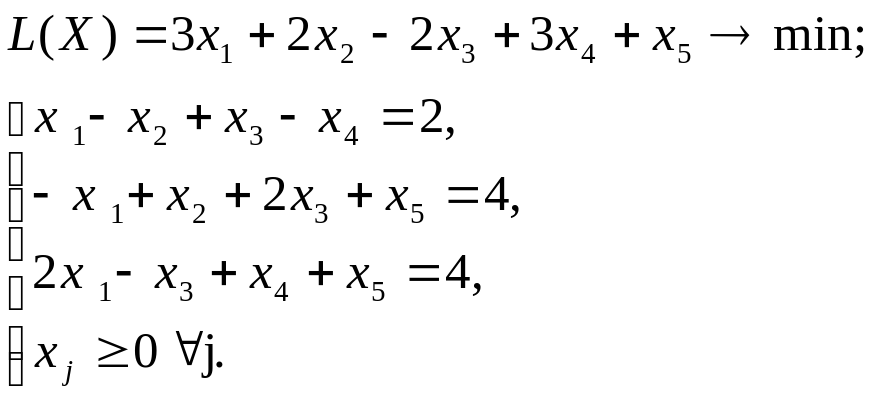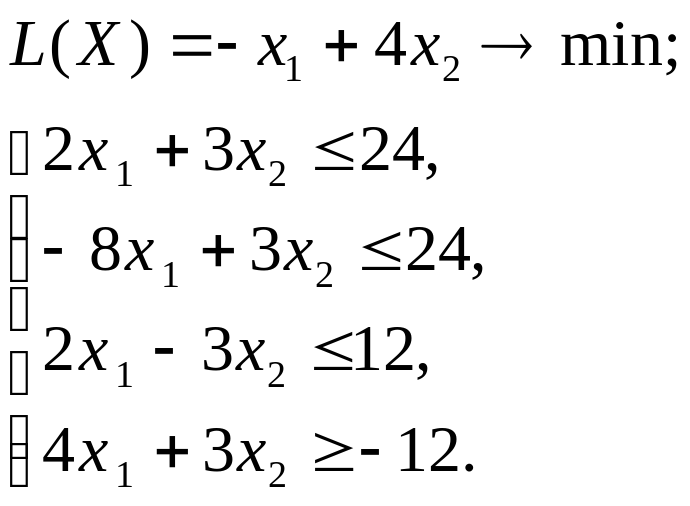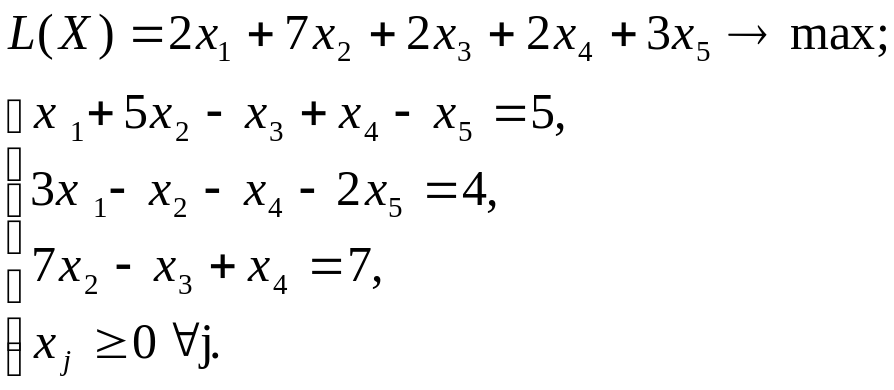Лабораторная работа №2
ЛАБОРАТОРНАЯ РАБОТА №2
“
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ОДНОИНДЕКСНЫХ ЗАДАЧ ” 2.1. ЦЕЛЬ РАБОТЫ
Приобретение навыков решения задач линейного программирования графическим методом.
2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Согласно номеру своего варианта выберите условие задачи и найдите оптимальное решение графическим методом.
2. Найдите оптимальное решение задачи в Excel.
3. Оформите отчет по лабораторной работе, который должен содержать:
титульный лист;
исходные данные варианта;
решение задачи;
результаты решения задачи.
2.3. ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП ГРАФИЧЕСКИМ МЕТОДОМ
Рассмотрим пример нахождения оптимального решения графическим методом для следующей задачи линейного программирования:
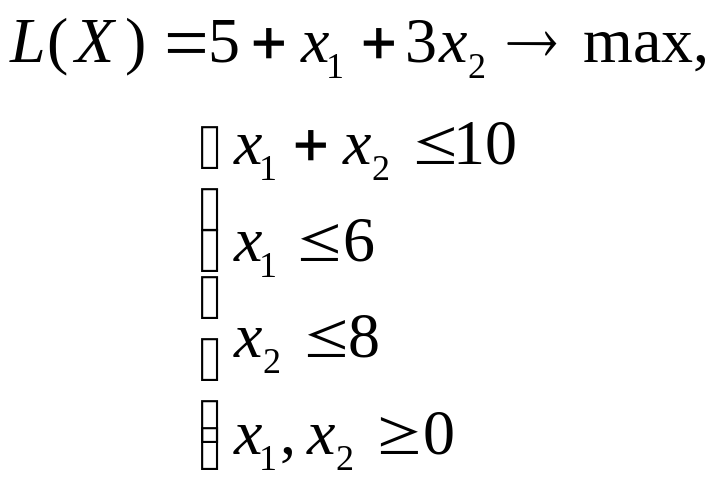
Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
1. В столбце А, начиная с ячейки А2, задаем последовательность значений переменной x1 как арифметическую прогрессию с первым членом, равным нулю, разностью 0,2, предельным значением 6.
2. В ячейке В2 вводим формулу =10-А2 и копируем ее в столбце В. Прямые х1=6, х2=8 зададим позже, как границы рисунка.
3. Вводим в ячейку С2 формулу линии уровня =($D$2-5-A2)/3 и копируем ее в столбце С.
4. В ячейке D2 вводим значение 0.
5. Выделяем диапазон А2:С32 и «Мастером диаграмм» строим точечную диаграмму:
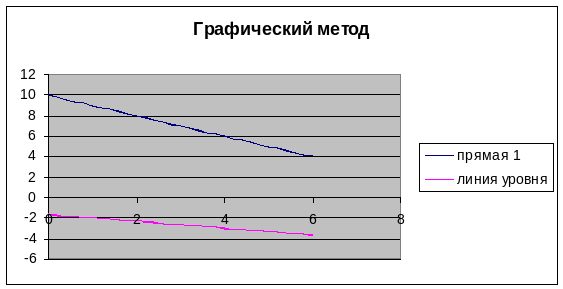
6. Убираем лишнее через контекстное меню:
Командами Формат оси Шкала открываем диалоговое окно:
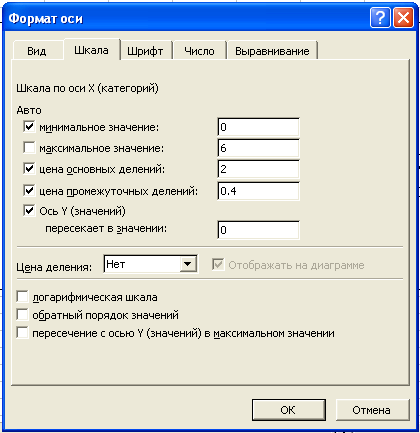
Устанавливаем в нем максимальное значение: 6, нажимаем ОК. Аналогично по оси Y задаем минимальное значение 0, максимальное значение 8.
Приводим диаграмму к виду, показанному на рисунке:
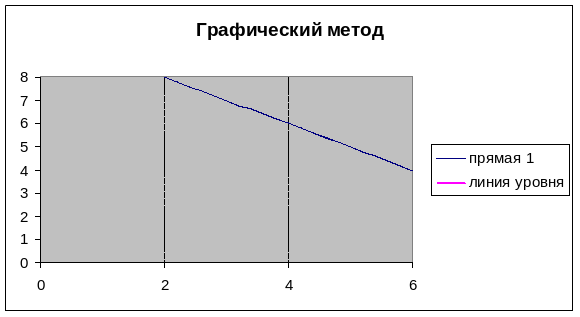
7. Изменяя значения ячейки D2, передвигаем линию уровня в сторону выхода из области допустимых решений:
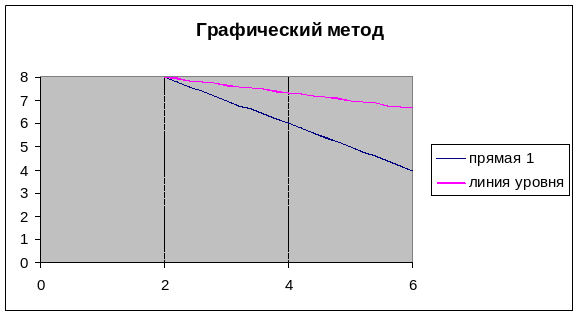
Из диаграммы видно, что точкой выхода линии уровня из многоугольника допустимых решений является точка (2; 8).
Графическим методом можно решить задачи ЛП, записанные в каноническом виде и удовлетворяющие условию 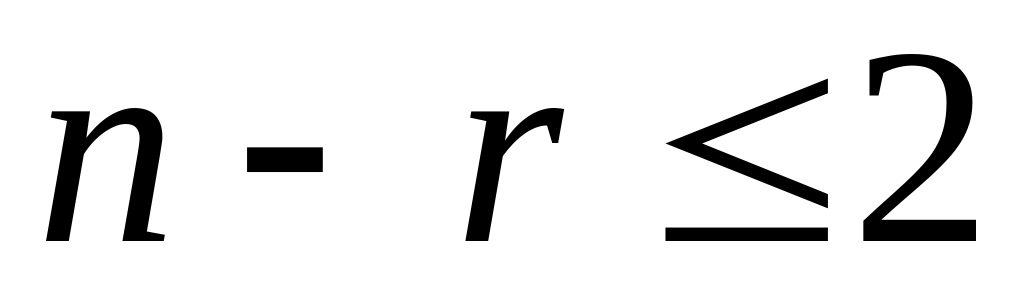 , где n – число неизвестных системы ограничений; r – ранг системы векторов условий.
, где n – число неизвестных системы ограничений; r – ранг системы векторов условий.
Рассмотрим пример решения задачи ЛП:
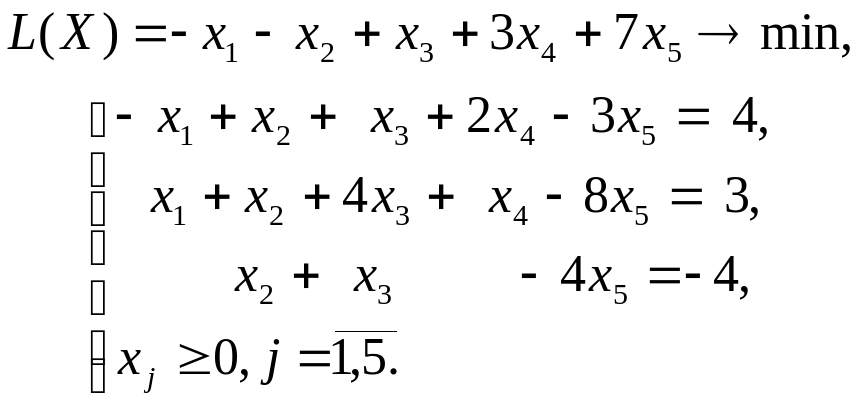
Графический метод применим, так как 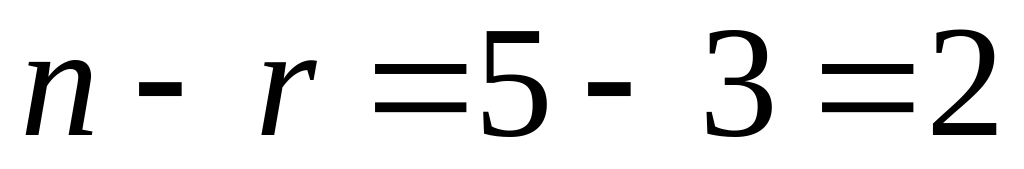 . Методом Жордана-Гаусса приведем систему уравнений-ограничений задачи к равносильной разрешенной.
. Методом Жордана-Гаусса приведем систему уравнений-ограничений задачи к равносильной разрешенной.
Введем расширенную матрицу системы ограничений и коэффициенты целевой функции в диапазон B2:G5:

В ячейке В7 зададим формулу =B2/$B$2 и методом «протаскивания» маркера заполнения скопируем ее в ячейки С7:G7:
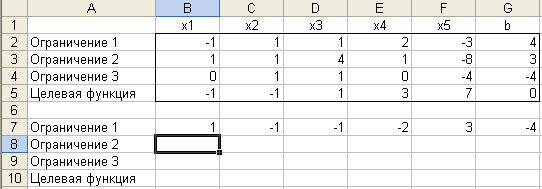
Тем самым первая строка расширенной матрицы системы ограничений разделена на -1 и выделен разрешающий элемент 1.
Замечание. Если в диапазоне В7:G7 окажутся результаты в форме десятичных дробей, то откройте контекстное меню и в диалоговом окне «Формат ячеек» установите формат числа «Дробный», со знаменателем до двух (или трех) цифр.
Далее в ячейку В8 вводим формулу =B3-B$7*$B3. Копируем ее, методом «протаскивания» маркера заполнения, в остальные ячейки диапазона С8:G8, делаем такие же элементарные преобразования диапазонов (строк) В4:G4 и В5:G5, получаем нули ниже разрешающего элемента:
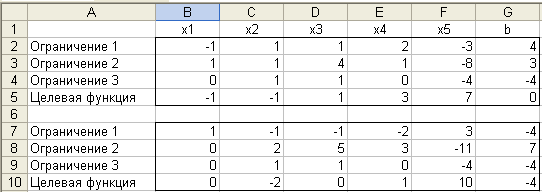
В ячейку С13 вводим формулу =C8/$C$8 и методом «протаскивания» маркера заполнения копируем ее в остальные ячейки диапазона В13:G13, что дает:
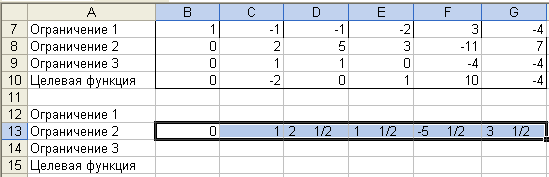
В ячейке С14 задаем формулу =C9-C$13*$C9 и копируем ее в остальные ячейки диапазона В14:G14. Далее проводим аналогичные элементарные преобразования диапазонов В12:G12 и В15:G15:
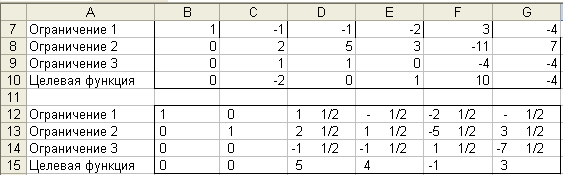
Повторяя алгоритм, приходим к окончательному результату:
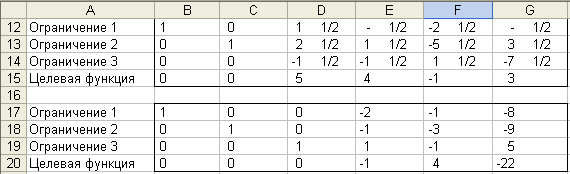
Задача ЛП после преобразований имеет вид:
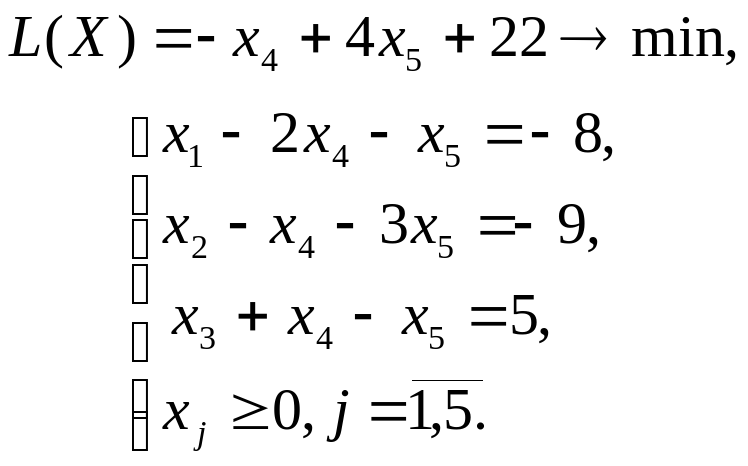
Отбросим в уравнениях-ограничениях неотрицательные разрешенные неизвестные х1, х2, х3 и заменим знак равенства знаками неравенства «», получим вспомогательную задачу ЛП с двумя переменными
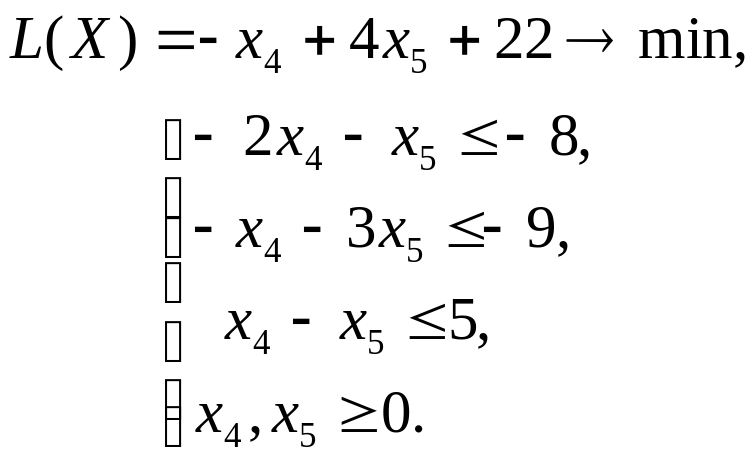
Далее она решается аналогично, как в первом примере, графическим методом.
2.4. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ
1. Каковы основные этапы решения задач ЛП графическим методом?
2. Как определить, какая полуплоскость отвечает линейному неравенству?
3. Что называется областью допустимых решений?
4. Какая линия называется линией уровня?
5. Как определить максимальное и минимальное значения линейной целевой функции в области допустимых решений?
6. Какие случаи возможны при решении задачи ЛП графическим методом?
7. В каких случаях задачу линейного программирования можно решить графическим методом?
2.5. ВАРИАНТЫ
Используя MS Excel, найти решение графическим методом для задачи ЛП, соответствующей заданному варианту (табл.3.1).
Таблица 3.1
Варианты задач к лабораторной работе №3
| № варианта | Математическая модель |
| 1 | 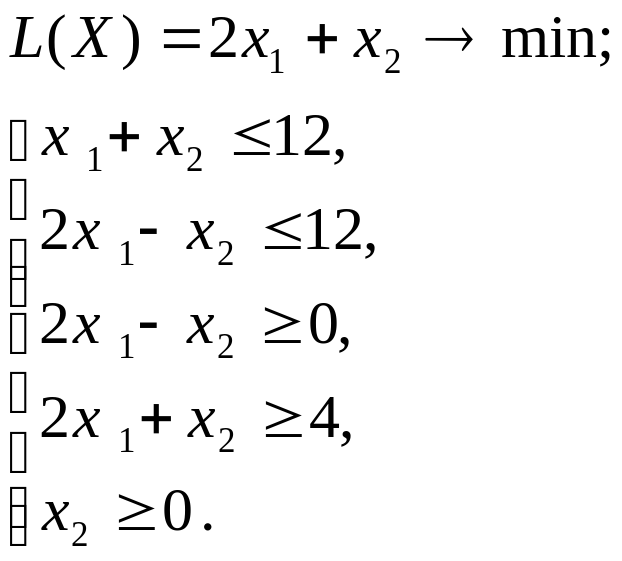 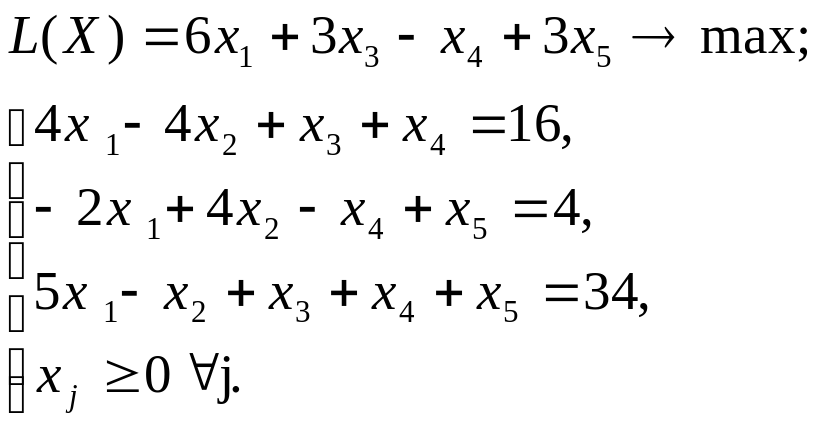
|
| 2 | 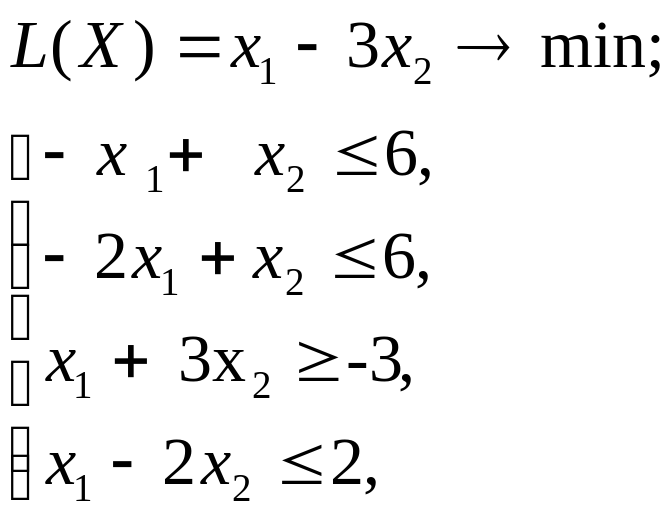 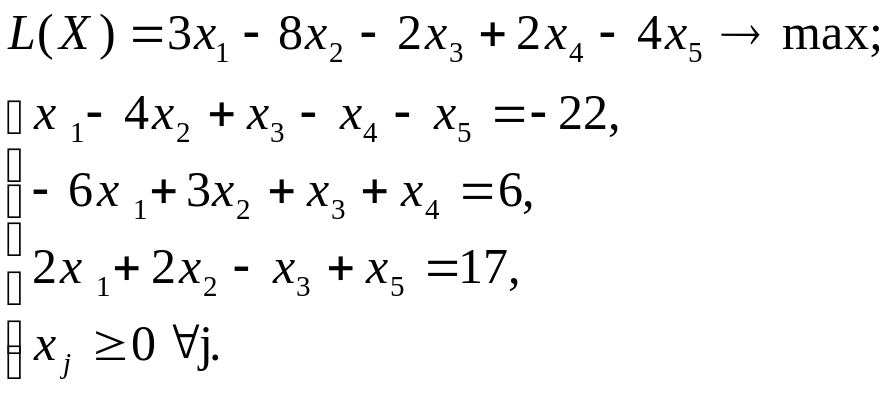
|
9