Графический способ решения задач с параметром в ЕГЭ по профильной математике. Пример 3.

Графический способ решения задач с параметром в ЕГЭ по профильной математике

Пример 3

Задача из открытого банка заданий ФИПИ

Найти все значения при каждом из которых система уравнений имеет более двух решений

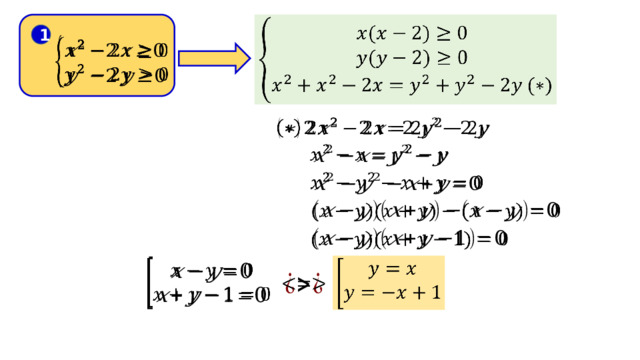
Шаг 1. Построим график первого уравнения системы

Раскроем модуль по определению для четырёх случаев:

3

2

1

4

1

1

?

1

1

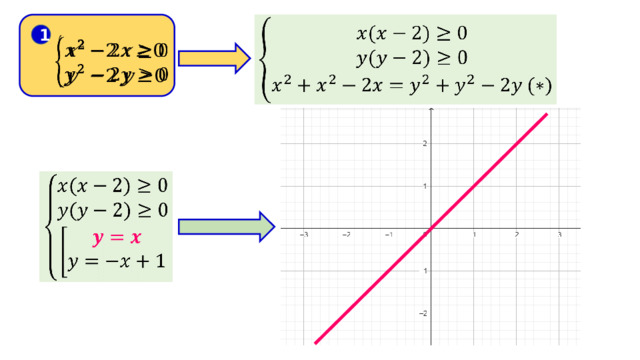
1

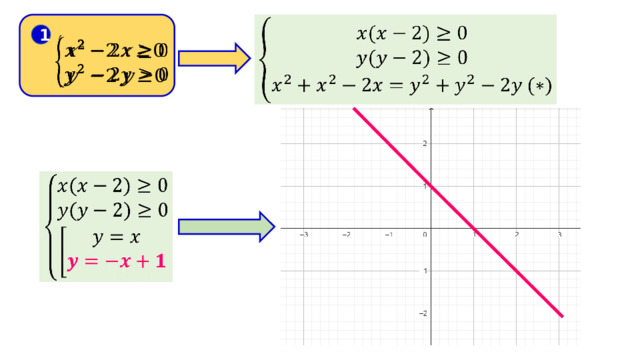
1

1

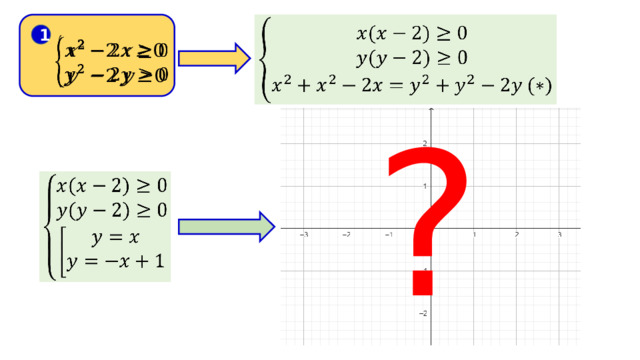
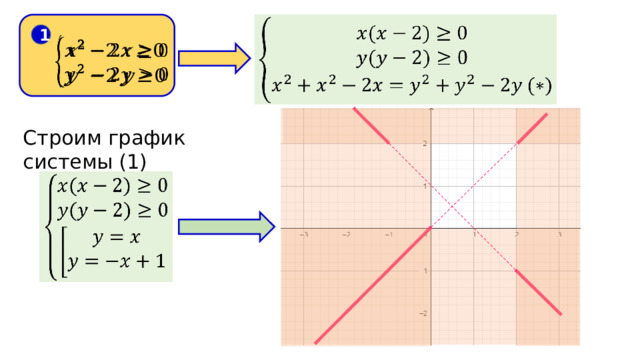
Строим график системы (1)

2

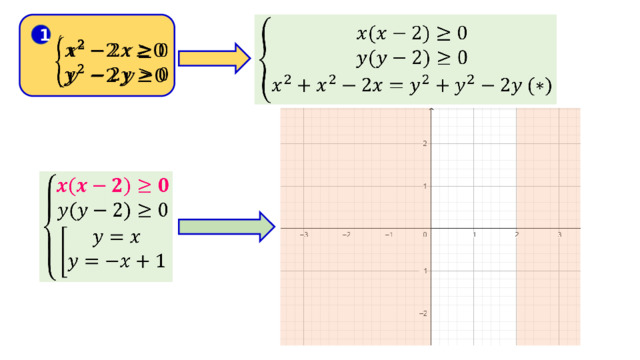
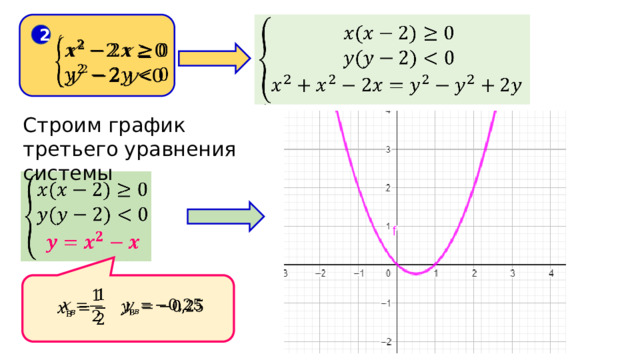
Строим график третьего уравнения системы

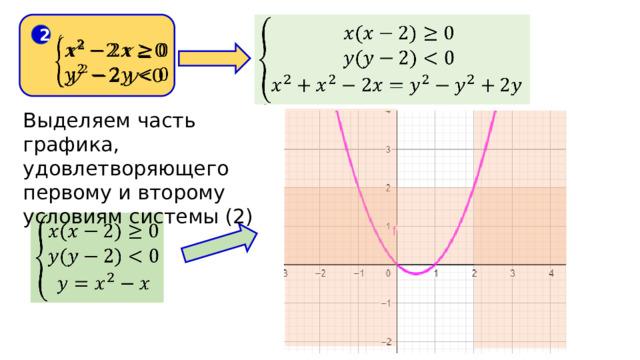
2

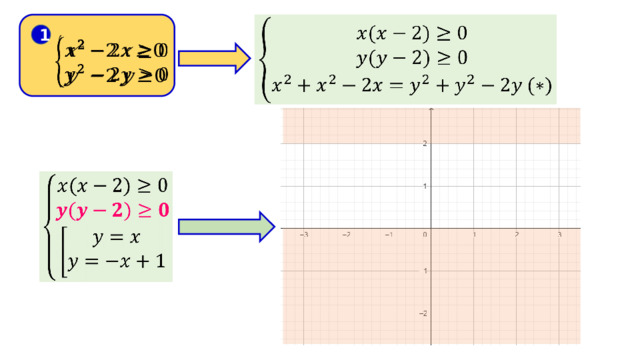
Выделяем часть графика, удовлетворяющего первому и второму условиям системы (2)

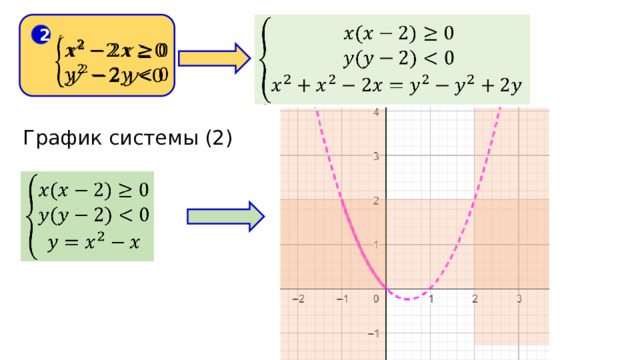
2

График системы (2)

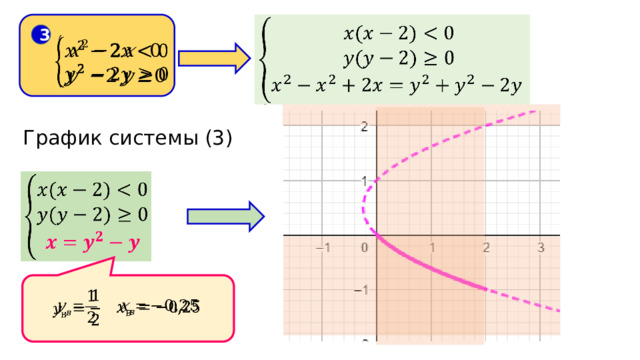
3

График системы (3)

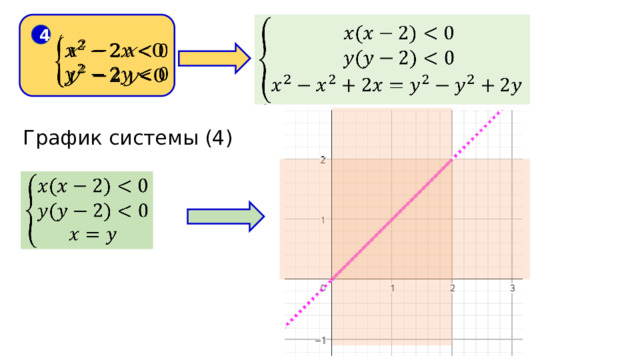
4

График системы (4)

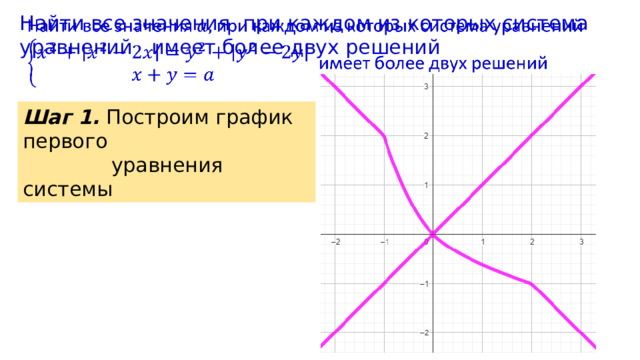
Найти все значения при каждом из которых система уравнений имеет более двух решений

Шаг 1. Построим график первого

уравнения системы

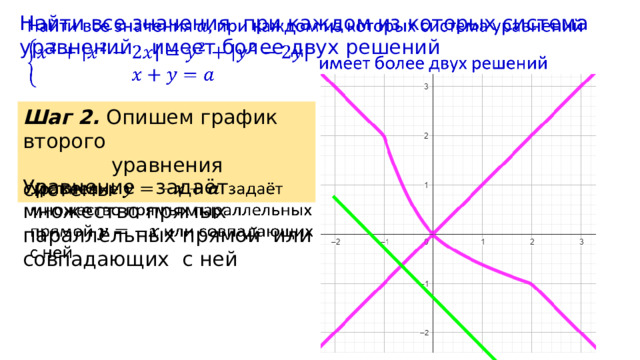
Найти все значения при каждом из которых система уравнений имеет более двух решений

Шаг 2. Опишем график второго

уравнения системы

Уравнение задаёт множество прямых параллельных прямой или совпадающих с ней

Найти все значения при каждом из которых система уравнений имеет более двух решений

Шаг 2. Проанализируем

количество общих точек

графиков уравнений

системы, а значит и

количество решений

системы

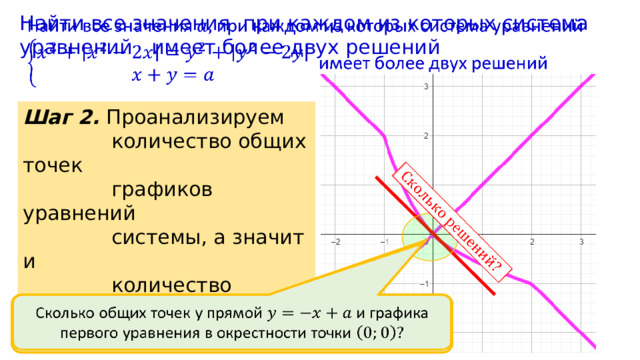
Найти все значения при каждом из которых система уравнений имеет более двух решений

Шаг 2. Проанализируем

количество общих точек

графиков уравнений

системы, а значит и

количество решений

системы

Сколько общих точек у прямой и графика первого уравнения в окрестности точки

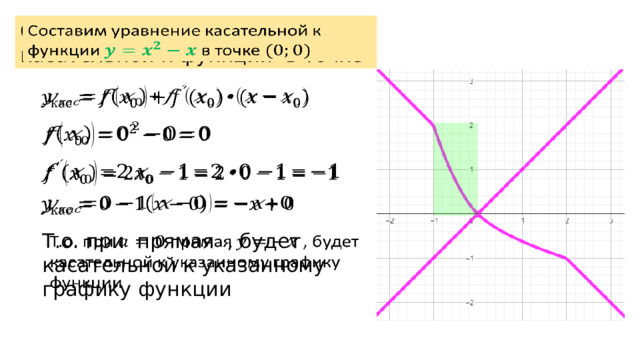
Составим уравнение касательной к функции в точке

Т.о. при прямая , будет касательной к указанному графику функции

Т.к. график первого уравнения системы симметричен относительно прямой , то прямая будет касательной и для кривой в точке

Т.о. при прямая , имеет с графиком первого уравнения системы ровно одну общую точку

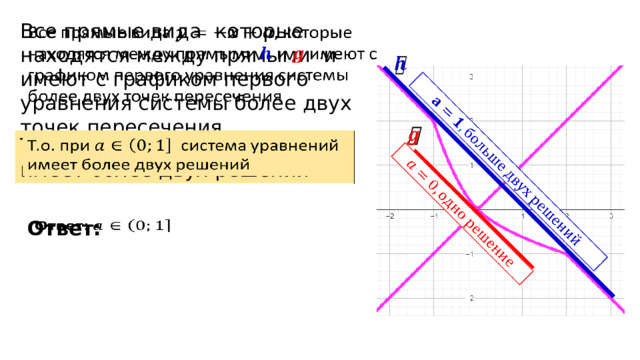
Все прямые вида которые находятся между прямыми и имеют с графиком первого уравнения системы более двух точек пересечения

Т.о. при система уравнений имеет более двух решений

Ответ: