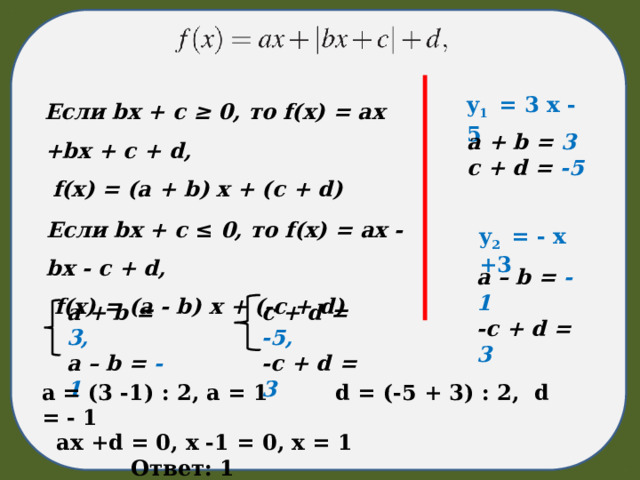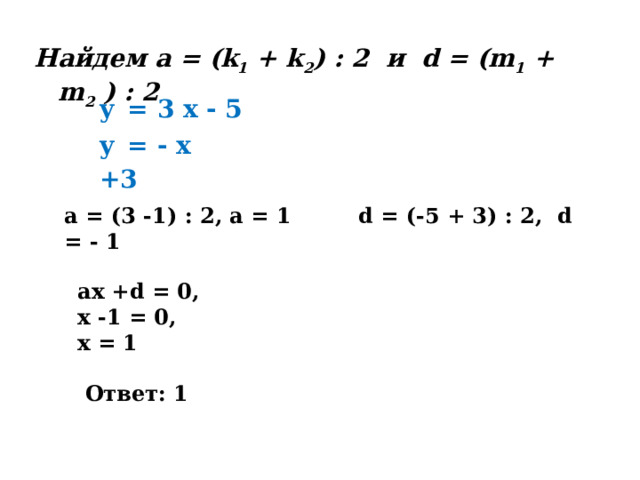Графики функций.
Кусочно-линейная функция.
Задание 9 ЕГЭ 2022.
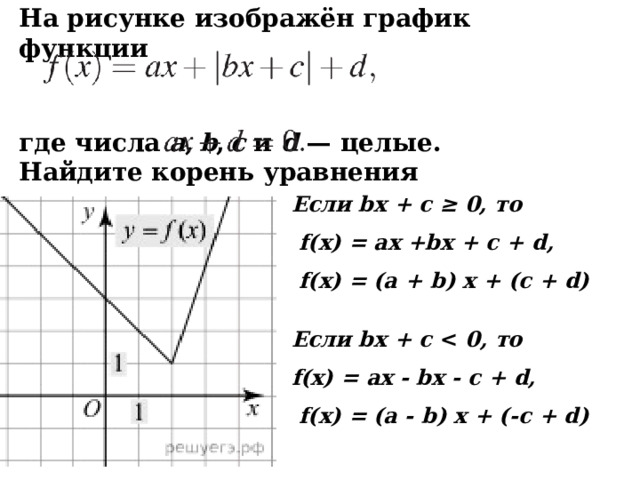
На рисунке изображён график функции
где числа a , b , c и d — целые. Найдите корень уравнения
Если bx + c ≥ 0, то
f(x) = ax +bx + c + d,
f(x) = (a + b) x + (c + d)
Если bx + c 0, то
f(x) = ax - bx - c + d,
f(x) = (a - b) x + (-c + d)

План решения
- Составить уравнения прямых
y 1 = k 1 x + m 1 и y 2 = k 2 x + m 2
2. Hайти а = (k 1 + k 2 ) : 2 и d = (m 1 + m 2 ) : 2
(как среднее арифметическое для «а» – угловых коэффициентов прямых,
для «d» - свободных членов)
3. Cоставить уравнение ax + d = n и решить его.
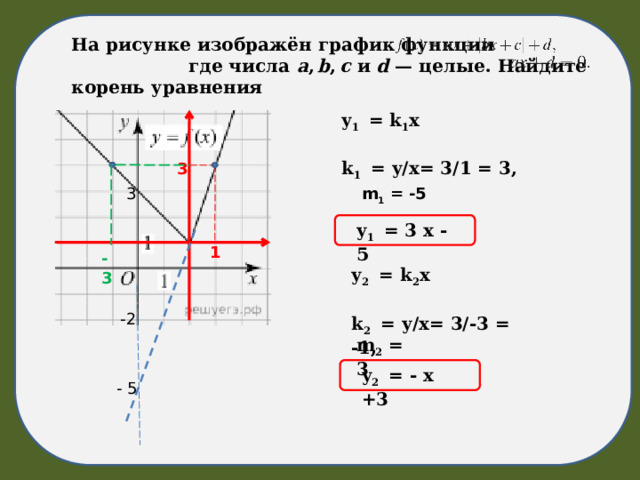
На рисунке изображён график функции где числа a , b , c и d — целые. Найдите корень уравнения
y 1 = k 1 x
k 1 = y/x= 3/1 = 3,
3
m 1 = -5
3
y 1 = 3 x - 5
1
-3
y 2 = k 2 x
k 2 = y/x= 3/-3 = -1,
-2
m 2 = 3
y 2 = - x +3
- 5
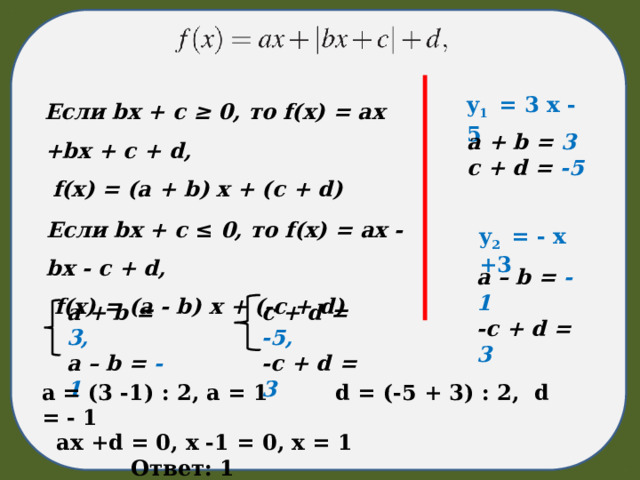
Если bx + c ≥ 0, то f(x) = ax +bx + c + d,
f(x) = (a + b) x + (c + d)
y 1 = 3 x - 5
a + b = 3
c + d = -5
Если bx + c ≤ 0, то f(x) = ax - bx - c + d,
f(x) = (a - b) x + (-c + d)
y 2 = - x +3
a – b = - 1
-c + d = 3
a + b = 3,
c + d = -5,
a – b = - 1
-c + d = 3
a = (3 -1) : 2, a = 1 d = (-5 + 3) : 2, d = - 1
ax +d = 0, x -1 = 0, x = 1 Ответ: 1

Уравнение прямой, проходящей через две точки
Пусть в плоскости заданы две точки М(х 1 ; у 1 ) и К(х 2 ;у 2 ), тогда уравнение прямой, проходящей через эти точки, имеет вид:
Если какой-либо из знаменателей равен нулю, следует приравнять к нулю соответствующий числитель

На рисунке изображён график функции
где числа a , b , c и d — целые. Найдите корень уравнения
- Составим уравнение прямой АВ: А(3;4), В(2;1)
А
В
y = 3 x - 5

На рисунке изображён график функции
где числа a , b , c и d — целые. Найдите корень уравнения
2) Составим уравнение прямой СВ: С(0;3), В(2;1)
А
С
В
y = - x +3
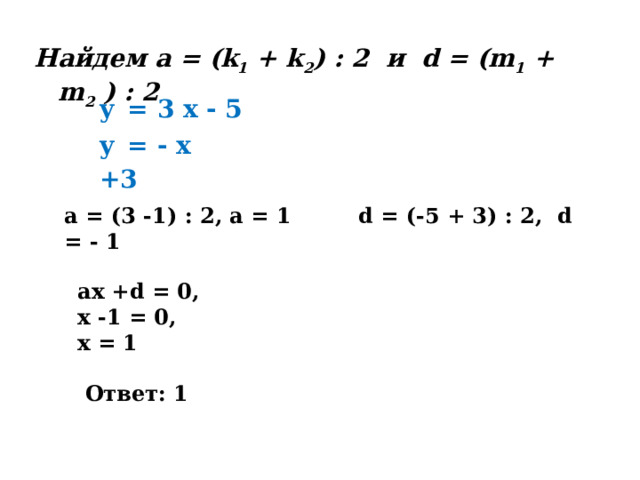
Hайдем а = (k 1 + k 2 ) : 2 и d = (m 1 + m 2 ) : 2
y = 3 x - 5
y = - x +3
a = (3 -1) : 2, a = 1 d = (-5 + 3) : 2, d = - 1
ax +d = 0,
x -1 = 0,
x = 1
Ответ: 1
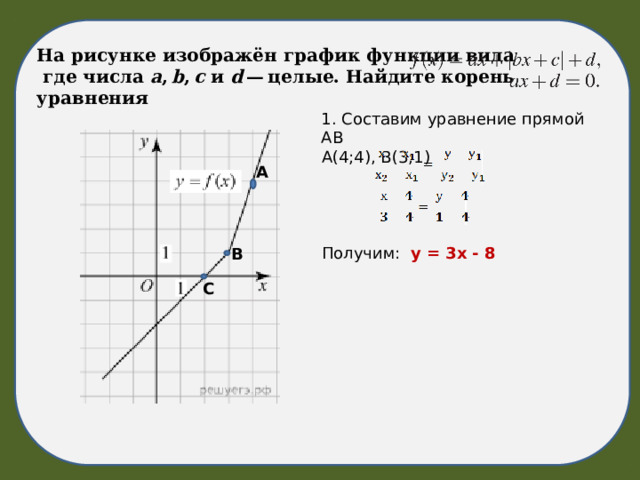
На рисунке изображён график функции вида
где числа a , b , c и d — целые. Найдите корень уравнения
1. Составим уравнение прямой АВ
А(4;4), В(3;1)
Получим: у = 3х - 8
А
В
С
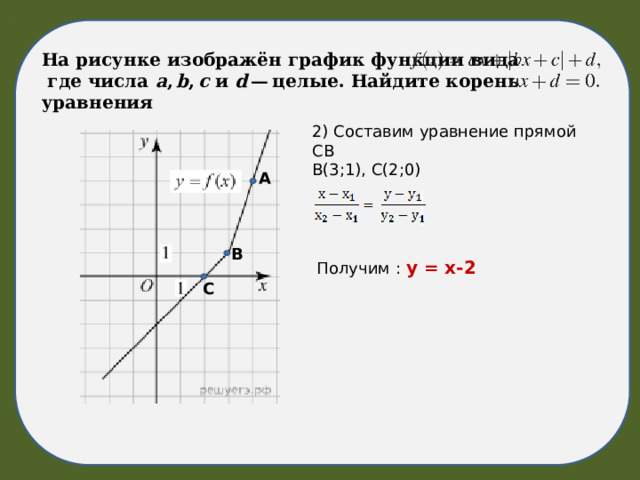
На рисунке изображён график функции вида
где числа a , b , c и d — целые. Найдите корень уравнения
2) Составим уравнение прямой СВ
В(3;1), С(2;0)
А
В
Получим : у = х-2
С
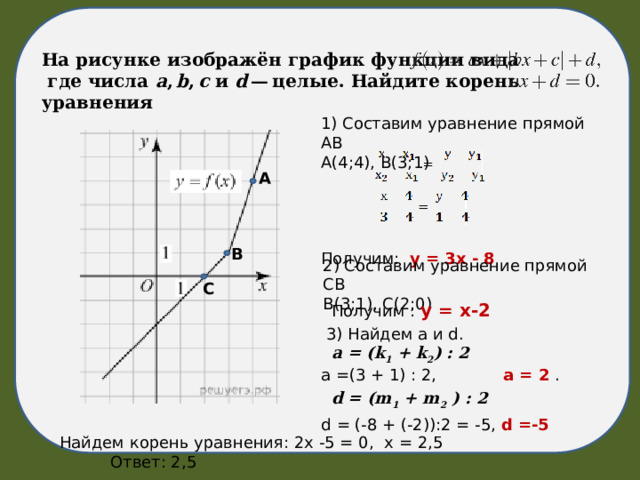
На рисунке изображён график функции вида
где числа a , b , c и d — целые. Найдите корень уравнения
- а)Составим уравнение прямой АВ
А(4;4), В(3;1)
Получим: у = 3х - 8
А
В
б) Составим уравнение прямой СВ
В(3;1), С(2;0)
С
Получим : у = х-2
На рисунке изображён график функции вида
где числа a , b , c и d — целые. Найдите корень уравнения
1) Составим уравнение прямой АВ
А(4;4), В(3;1)
Получим: у = 3х - 8
А
В
2) Составим уравнение прямой СВ
В(3;1), С(2;0)
С
Получим : у = х-2
3) Найдем а и d.
а = (k 1 + k 2 ) : 2
а =(3 + 1) : 2, а = 2 .
d = (m 1 + m 2 ) : 2
d = (-8 + (-2)):2 = -5, d =-5
Найдем корень уравнения: 2х -5 = 0, х = 2,5 Ответ: 2,5

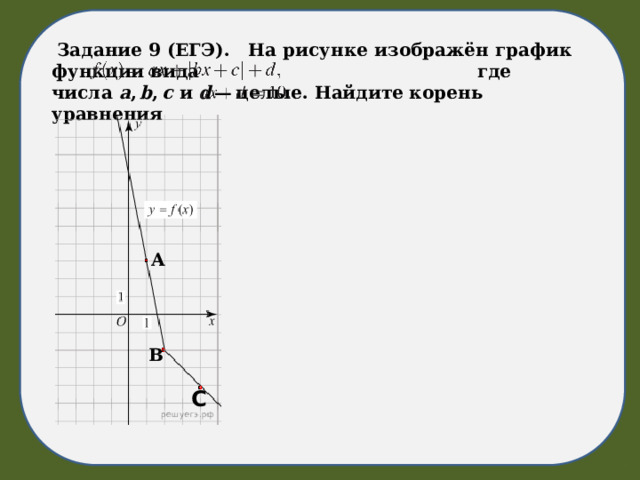
Задание 9 (ЕГЭ). На рисунке изображён график функции вида где числа a , b , c и d — целые. Найдите корень уравнения
А
В
С

Задание 9(ЕГЭ). На рисунке изображён график функции вида где числа a , b , c и d — целые. Найдите корень уравнения
Решение
Уравнение прямой АВ : у = -5х +8
Уравнение прямой ВС: у = -х
а = (-5-1):2, а = -3
d = (8+0):2 = 4, d= 4
Уравнение: -3х + 4 = 10. Откуда х = -2
Ответ: -2
А
В
С
Задание 9 (ЕГЭ). На рисунке изображён график функции вида где числа a , b , c и d — целые. Найдите корень уравнения
Решение
Уравнение прямой АВ : у = -5х +8
Уравнение прямой ВС: у = -х
Откуда b = -2
Решая, получим с = 4
Уравнение: -2х + 4 = 0. Откуда х = 2
Ответ: 2
a + b = -5,
a + b = -5,
- a + b = 1,
a – b = - 1
А
c + d = 8,
c + d = 8,
-c + d = 0
c - d = 0,
В
С
! Обратите внимание: 2 – абсцисса точки излома
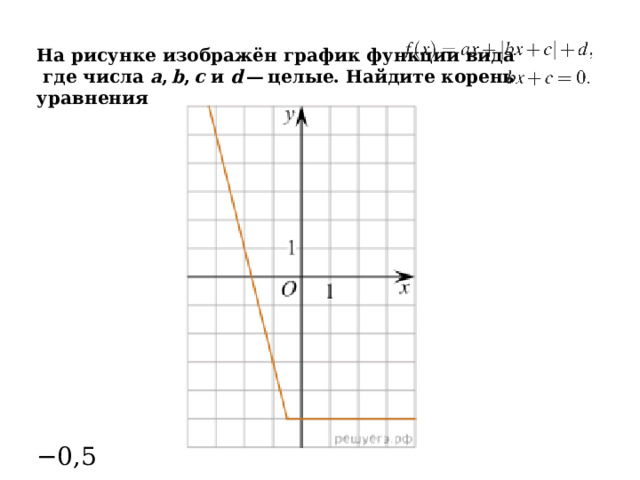
На рисунке изображён график функции вида
где числа a , b , c и d — целые. Найдите корень уравнения
− 0,5

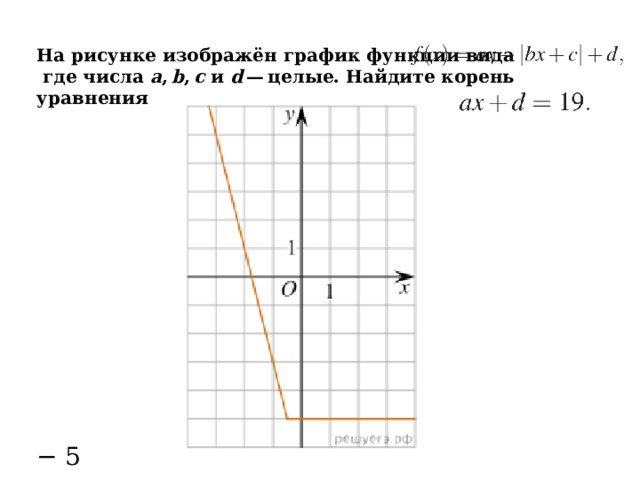
На рисунке изображён график функции вида
где числа a , b , c и d — целые. Найдите корень уравнения
− 5