Причёсывание задач (или «можно считать, что. . . »)
Известно, что человек некультурный ест как придётся, а культурный сначала приготовит пищу. Так и некультурный математик решает задачу как придётся, а культурный «приготовит» задачу, т. е. преобразует её к удобному для решения виду. Приготовление задачи может состоять в переформулировке условия на более удобном языке (например, на языке графов), отщеплении простых случаев, сведении общего случая к частному. Такие преобразования сопровождаются фразами «в силу симметрии», «явно не хуже», «для определённости», «не нарушая общности», «можно считать, что. . . ».
Пример 1. Каждый ученик класса ходил хотя бы в один из двух походов. В каждом походе мальчиков было не больше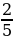 . Докажите, что во всём классе мальчиков не больше
. Докажите, что во всём классе мальчиков не больше 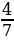 .
.
Решение. «Лобовое» решение состоит в рассмотрении количеств мальчиков, ходивших только в первый поход, ходивших только во второй поход, ходивших в оба похода, то же для девочек, составлении и решении системы уравнений и неравенств. Этого делать не хочется, поэтому будем избавляться от лишних параметров, сводя задачу к её частному случаю. Мы проделаем это в несколько шагов. После каждого шага упрощения становится очевидным следующий шаг.
Будем увеличивать число мальчиков в классе, не изменяя числа девочек и не нарушая условия задачи.
1 шаг. «Впишем» всех девочек в число участников обоих походов. От этого доля мальчиков в походах уменьшится, а в классе – не изменится. Это позволит добавить новых мальчиков в каждый поход, увеличив их долю в классе. Итак, можно считать, что все девочки ходили в оба похода.
2 шаг. Если мальчик ходил в первый поход, то освободим его от посещения второго. Доля мальчиков в походе уменьшится. Добавим новых мальчиков в пределах 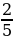 участников походов. Итак, можно считать, что каждый мальчик ходил только в один поход.
участников походов. Итак, можно считать, что каждый мальчик ходил только в один поход.
3 шаг. Если в одном походе было меньше мальчиков, чем в другом, то добавим в класс мальчиков. Доля мальчиков в походах останется не больше 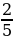 , а доля мальчиков в классе увеличится. Можно считать, что мальчиков было в походах поровну.
, а доля мальчиков в классе увеличится. Можно считать, что мальчиков было в походах поровну.
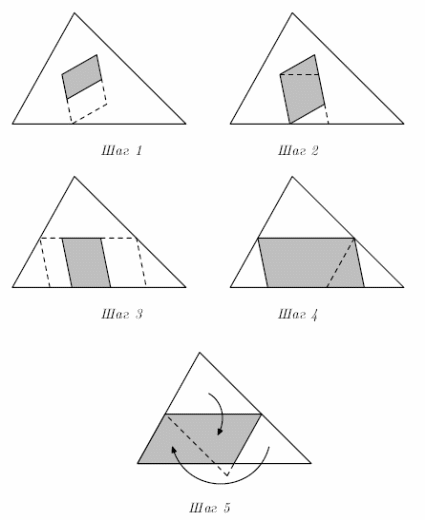
4 шаг. Задача стала тривиальной: в обоих походах были все девочки и ровно половина мальчиков. Обозначим число девочек 3x, тогда мальчиков в походах было не больше 2x, а во всём классе – не больше 4x. Максимальное число мальчиков в классе 4x, а это 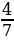 класса.
класса.
Пример 2. Из бумажного треугольника вырезали параллелограмм. Докажите, что его площадь не превосходит половины площади треугольника.
Решение. Трудность состоит в том, что положение параллелограмма внутри треугольника произвольное. Будем преобразовывать параллелограмм, не уменьшая его площадь (рис. ниже).
1 шаг. «Удлиним» параллелограмм так, чтобы одна его вершина попала на сторону треугольника.
2 шаг. Перекроим параллелограмм, не меняя его площади, так, чтобы его сторона попала на сторону треугольника.
3 шаг. «Удлиним» параллелограмм вдоль общей с треугольником стороны так, чтобы все четыре вершины попали на стороны треугольника.
4 шаг. Перекроим параллелограмм, не меняя его площади, так, чтобы один его угол совпал с углом треугольника.
5 шаг. Теперь задача решается легко. Например, покроем параллелограмм дополняющими его треугольниками (один из треугольников отражается центрально симметрично относительно середины его общей с параллелограммом стороны, а второй параллельно переносится).
Пример 3. В 9 ячейках записаны числа: в первой – единица, в остальных – нули. За одну операцию можно выбрать две ячейки и заменить каждое число в них полусуммой этих чисел. Какое наименьшее число можно получить в первой ячейке?
Решение. Нетрудно получить число 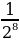 , усредняя число в первой ячейке со всеми остальными по очереди. Труднее доказать, что меньше получить нельзя.
, усредняя число в первой ячейке со всеми остальными по очереди. Труднее доказать, что меньше получить нельзя.
Изменим условие задачи. Пусть после каждой операции все ненулевые числа становятся равными наименьшему из них. Эта новая операция даёт результат в каждой ячейке не больше, чем исходная операция.
Теперь всё ясно: новая операция либо ничего не меняет (если числа равны), либо уничтожает один нуль и уменьшает все числа в два раза. Поскольку новая операция не позволяет получить число меньшее 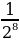 , то исходная операция – тем более.
, то исходная операция – тем более.
Задачи для самостоятельного решения
1. В кладовой лежат 300 сапог: 100 хромовых, 100 кирзовых и 100 яловых, причём левых и правых поровну – по 150. Докажите, что из имеющихся сапог можно составить по крайней мере 50 пар.
2. Из бумажного параллелограмма вырезали треугольник. Докажите, что его площадь не превосходит половины площади параллелограмма.
3. На плоскости нарисовано несколько точек. Двое по очереди соединяют их отрезками. Отрезки могут выходить из одной точки, но не должны пересекаться. Кто не может сделать ход, проигрывает. Докажите, что при любых ходах игроков победителем будет один и тот же, а кто именно – определяется лишь начальной позицией.
Указание. Игра заканчивается, если рисунок представляет собой многоугольник, разбитый на треугольники.
4. Дан выпуклый многоугольник площади 9. Его пересекают десять параллельных прямых на расстоянии 1 друг от друга. Докажите, что сумма длин отрезков, высеченных многоугольником на этих прямых, не более десяти.
5. В кубе покрашено более половины вершин. Ребро называется покрашенным, если покрашены обе ограничивающие его вершины. Докажите, что покрашено не менее трёх рёбер. (Аналогично, в n-мерном кубе покрашено не менее n рёбер.)
6. Дан многогранник с n вершинами и точка A внутри него. Пусть 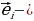 единичный вектор, направленный из точки A к i-й вершине многогранника. Докажите, что
единичный вектор, направленный из точки A к i-й вершине многогранника. Докажите, что
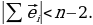
7. Алфавит некоторого языка состоит из n букв. Известно, 12 Идеи и методы решения задач что ни одно слово не является началом другого. ak 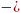 число слов языка, состоящих из k букв. Докажите, что
число слов языка, состоящих из k букв. Докажите, что 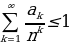 .
.
Указание. Попробуйте заменить слова максимальной длины на меньшие слова.







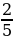 . Докажите, что во всём классе мальчиков не больше
. Докажите, что во всём классе мальчиков не больше 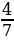 .
. 
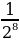 , усредняя число в первой ячейке со всеми остальными по очереди. Труднее доказать, что меньше получить нельзя.
, усредняя число в первой ячейке со всеми остальными по очереди. Труднее доказать, что меньше получить нельзя. 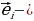 единичный вектор, направленный из точки A к i-й вершине многогранника. Докажите, что
единичный вектор, направленный из точки A к i-й вершине многогранника. Докажите, что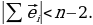
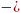 число слов языка, состоящих из k букв. Докажите, что
число слов языка, состоящих из k букв. Докажите, что 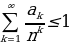 .
. 









