муниципальное бюджетное общеобразовательное учреждение
«Тирянская основная школа»
Кардымовского района Смоленской области
Индивидуальный итоговый проект
по геометрии на тему
«Некоторые практические применения геометрии»
Работу выполнила
обучающаяся 9 класса
Кезикова Мария
Руководитель
Кезикова Л.Н.
2018/2019 учебный год
План
| 1. Пояснительная записка | стр. 2 |
| 2. Применение подобия треугольников | стр. 6 |
| 2.1. Определение высоты предмета методом Фалеса | стр. 6 |
| 2.2. Определение высоты предмета с помощью зеркала | стр. 7 |
| 2.3. Определение высоты предмета с помощью равнобедренного треугольника | стр. 7 |
| 2.4. Высотомер лесника | стр. 8 |
| 2.5. Определение высоты предмета высотомером, не приближаясь к дереву | стр. 8 |
| 2.6. Определение площади крыши | стр. 9 |
| 2.7. Определение расстояния до кораблей в море | стр. 9 |
| 2.8. Измерение школы различными способами | стр. 10 |
| 3. Геометрия в медицине | стр. 12 |
| 3.1. Связь геометрии и медицины | стр. 12 |
| 3.2. Измерение площади верхней конечности (руки) | стр. 13 |
| 4. Наука психогеометрия | стр. 15 |
| 4.1. Геометрия в психологии | стр. 15 |
| 4.2. Тестирование школьников | стр. 15 |
| 5. Заключение | стр. 17 |
| 6. Список литературы | стр. 18 |
1. Пояснительная записка
“Я думаю, что никогда до настоящего
времени мы не жили в такой
геометрический период.
Все вокруг – геометрия”
Эти слова, сказанные великим французским архитектором Корбюзье в начале 20 века, очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Современные здания и космические станции, подводные лодки, интерьеры квартир и бытовая техника – всё имеет геометрическую форму. Геометрические знания являются сегодня профессионально значимыми для многих современных специальностей: для дизайнеров и конструкторов, для рабочих и учённых. Мировая наука началась с геометрии. Ребёнок, ещё не научившийся говорить, познаёт геометрические свойства окружающего мира. Все время, когда мы имеем дело с формой, размером, положением предмета в пространстве, мы вовлечены в геометрию.
Эта наука зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, полученные из наблюдений и опытов. Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: «Не знающие геометрии не допускаются!»
А, сейчас большинство школьников не учат геометрию. Считают её очень трудным и не нужным предметом. Многие её просто не понимают, к тому же в геометрии много нужно учить наизусть и не просто «выучить», а уметь объяснить и применить при решении задач. Зачем?! Ученики считают, что ответы на все вопросы можно найти в интернете. Но, геометрический материал обязательно входит в курс экзамена по математике за 9 класс. Думаю, что это не случайно.
Гипотеза: современному человеку нужны геометрические знания.
Проблема: как доказать современным школьникам что надо учить геометрию.
Мне вспомнился такой интересный случай. В первом классе я смотрела детективный сериал «Детективное агентство Иван да Марья». В одной из серий следователь сказал, что преступник является «квадратом». Я подумала, что преступник крупного телосложения, но, когда он появился в кадре была очень удивлена – преступником оказался худой мужчина небольшого роста. Причем здесь квадрат?! Тогда ответа на данный вопрос я не нашла и со временем забыла об этом. Теперь я хочу разгадать эту тайну.
Изучив публикации в сети Интернет о практических применениях геометрии я узнала, что из тем школьного курса геометрии наиболее часто используется «подобие треугольников». Может ли оно пригодится человеку, профессия которого не связана с геометрией?
Во многих источниках упоминаются одни и те же профессии связанные с геометрией: архитектор, инженер, дизайнер, конструктор, модельер. Но, меня заинтересовал вопрос об использовании геометрических знаний, например, в медицине.
Поэтому, в своей работе я решила показать наиболее интересные, на мой взгляд, применения геометрии в нашей жизни: практические применения подобия треугольников; применение геометрии в медицине; применение геометрии в психологии. Считаю выбранную тему актуальной так как в учебнике геометрии содержится очень мало задач с практическим содержанием и возможно поэтому школьники не понимают зачем учить столько определений, теорем и формул если в дальнейшей жизни они не нужны. А в материалах ОГЭ по математике такие задачи встречаются в каждом варианте в первой части работы, причем, теоретический материал иногда нужно применить в нестандартном виде. Думаю, что работа над проектом поможет мне лучше ориентироваться в таких задачах и я смогу показать наиболее интересные применения геометрии в жизни.
Цель: найти наиболее интересные практические применения геометрии в современном мире.
Задачи:
1. Изучить публикации в сети Интернет по данной теме.
2. Систематизировать изученный материал.
3. Рассмотреть практические применения подобия треугольников.
4. Найти ответ на вопрос о применении геометрии в медицине.
5. Познакомиться с понятием «психогеометрия».
6. Применить полученные знания на практике.
7. Обобщить полученные результаты.
Я начала с изучения практического применения подобия треугольников. В учебнике геометрии рассмотрено вычисление высоты столба с помощью шеста и вращающейся планки, прикрепленной к шесту. Мне такой способ показался не очень удобным на практике, так как будет трудно определить пересечение продолжения планки с землей. Так же предлагается определить высоту дерева с помощью тени. А что делать, если погода не солнечная? Еще в одной задаче описано определение высоты дерева с помощью зеркала. Это уже более интересно. В своей работе я воспользовалась этим методом для определения высоты школы и нашла другие подходящие методы определения высоты предмета. Выяснилось что подобие треугольников применимо и для других целей. Подробнее об этом будет рассказано в соответствующей части работы.
Затем я приступила к изучению возможности использования геометрии в медицине. Находя информацию о связи геометрии с телом человека, я окунулась в целый мир удивительных открытий. Анатомия человеческого тела очень многогранна. В ней имеется множество различных элементов, отличающихся по местоположению, форме и составу. Для того чтобы дать более точное описание органу, структуре или образованию, в 19 веке в анатомию были введены такие геометрические понятия, как оси и плоскости. Благодаря установленной таким образом симметрии человеческого тела, облегчилось понимание его строения. Еще я узнала, что в химиотерапии для расчета дозы вводимого препарата площадь поверхности тела является более точным показателем, чем масса тела! Поэтому решила попробовать с помощью геометрического аппарата вычислить площадь своей руки и сравнить полученные результаты с данными из медицинских справочников. Для осуществления данной цели пришлось изучить формулы определения площади поверхности пространственных геометрических фигур.
Как же может быть связано описание человека с геометрической фигурой? Что имел в виду следователь, если внешность преступника совсем не подходила под внешность «квадрата»? В процессе поиска ответов на данные вопросы я наткнулась на интересное и незнакомое мне слово «психогеометрия». Оказалось, что существует целая наука, суть которой состоит в исследовании личности человека с помощью простых тестов, связанных с геометрическими фигурами. Так вот что имел в виду следователь!
2. Применение подобия треугольников
2.1. Определение высоты предмета методом Фалеса
В основе подобия фигур лежит принцип отношения и пропорции. Идея отношения и пропорции зародилась в глубокой древности. Об этом свидетельствуют древнеегипетские храмы, детали гробницы Менеса и знаменитых пирамид в Гизе (III тысячелетие до н. э.), вавилонские зиккураты (ступенчатые культовые башни), персидские Дворцы, Индийские и другие Памятники древности. Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V—IV вв. до н. э. трудами Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге «Начал» Евклида, начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».
Как, например, определить высоту предмета? Самый легкий и самый древний способ – без сомнения, тот, которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Фалес, – говорит предание, - избрал день и час, когда длина собственной его тени равнялась его росту; в этот момент высота пирамиды должна также равняться длине отбрасываемой ею тени. Конечно, длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить непосредственно. Фалес жил задолго до Евклида, автора замечательной книги, по которой обучались геометрии в течение двух тысячелетий после его смерти. Заключенные в ней истины не были открыты в эпоху Фалеса. А чтобы воспользоваться тенью для решения задачи о высоте пирамиды, надо было знать уже некоторые геометрические свойства треугольника, а именно следующие два: 1) что углы при основании равнобедренного треугольника равны, и обратно - что стороны, лежащие против равных углов треугольника, равны между собою; 2) что сумма углов всякого треугольника (или по крайней мере прямоугольного) равна двум прямым углам. Только вооруженный этим знанием Фалес вправе был заключить, что, когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и, следовательно, вершина пирамиды, середина ее основания и конец ее тени должны обозначать равнобедренный треугольник. Однако способ Фалеса в указанном виде применим не всегда.
Существует много способов определения высоты предмета с помощью подобия треугольников, не дожидаясь определенного положения солнца. Рассмотрим некоторые из них. В качестве измеряемого объекта возьмем дерево.
2.2. Определение высоты предмета с помощью зеркала
На некотором расстоянии от дерева на ровной земле кладётся зеркало, и отходят от него назад в такую точку, стоя в которой наблюдатель видит верхушку дерева (Приложение 3 слайд 3).
АВ – высота дерева
BС – расстояние от дерева до зеркала
CD – расстояние от человека до зеркала
ED – рост человека – 12 см (расстояние от макушки до уровня глаз).
Треугольник АВС подобен треугольнику DEC т.к. A = D (перпендикуляр), BCA = ECD (т. к. по закону отражения света угол падения равен углу отражения). Из подобия треугольников получаем пропорцию.
BС : CD = AB : ED , 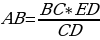
2.3. Определение высоты предмета с помощью равнобедренного треугольника
Для определения высоты предмета мы можем воспользоваться свойством равнобедренного прямоугольного треугольника. Для этого надо изготовить один простой прибор, его можно изготовить из дощечки и двух булавок (Приложение 3 слайд 4).
На дощечке любой формы намечают три точки – вершины равнобедренного прямоугольного треугольника.
В них втыкается по булавке.
К верхней булавке привязывается ниточка с грузиком.
Приближаясь к дереву или отдаляясь от него вы всегда найдете такое место А, из которого, глядя на булавки E и F, увидите, что они покрывают верхушку С дерева: это значит что продолжение гипотенузы EF проходит через точку С. Тогда, очевидно, расстояние ВE равно СВ, так как угол Е =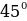 . Следовательно, измерив, расстояние ВE и прибавив OB, т.е. возвышение АЕ глаза над землей, получим искомую высоту дерева.
. Следовательно, измерив, расстояние ВE и прибавив OB, т.е. возвышение АЕ глаза над землей, получим искомую высоту дерева.
2.4. Высотомер лесника
Можно измерить высоту дерева с помощью специального прибора – высотомера (Приложение 3 слайд 5). Его можно легко изготовить:
Картонный или деревянный прямоугольник OMNQ.
На вершину M привязан грузик с ниточкой.
На краю ОQ нанести сантиметровые деления.
П
Рис. 7
одойдя к дереву держат высотомер так чтобы глядя вдоль края MN видеть на одной линии с ним вершину В дерева. В точке М привешен на нити грузик F. Находим точку Е в которой нить пересекает линию OQ . треугольники МВС и МОЕ подобны, так как оба прямоугольные и имеют равные острые углы МВС и МЕО (с соответственно параллельными сторонами), значит мы в праве написать пропорцию:
ВС : ЕО = МС : МО, отсюда ВС = МС*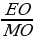 .
.
Так как МС, ЕО и МО можно измерить непосредственно, то легко получить искомую высоту дерева, прибавив длину нижней части СD ствола (высоту прибора над почвой)
2.5. Определение высоты предмета высотомером, не приближаясь к дереву
Высотомером можно измерять высоту деревьев, к которым нельзя подойти вплотную (Приложение 1 рисунок 1). Надо направить прибор на вершину В дерева из двух точек А и А1. П
Рис. 9
усть в точке А мы определили, что ВС = 0.9АС, а в точке А
1 – что ВС = 0,4А
1С. Тогда мы знаем, что AC =
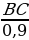
, A
1C =
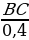
, откуда
AA1 = A1C – AC = 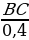 ––
–– 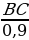 =
= 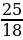 BC отсюда получаем, что BC =
BC отсюда получаем, что BC = 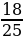 AA1.
AA1.
2.6. Определение площади крыши
Подобие треугольников можно применить и для определения площади крыши. Можно, конечно, туда залезть, но, гораздо проще сделать это с поверхности земли. Нужно произвести не сложные измерения: длину и ширину основания строения можем измерить непосредственно, а высоту подъема рассчитаем с помощью подобия треугольников.
На рисунке (Приложение 1 рисунок 2): a - длина основания строения, b - ширина основания строения, BD = c - высота подъема, d - длина свеса, AC - длина крыши, AB - ширина крыши.
Исходя из теоремы Пифагора получим ширину шиферного (или другого) покрытия:
AD = b : 2 + d; AC = a + 2d; AB = 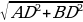 и S = AC ∙ AB
и S = AC ∙ AB
2.7. Определение расстояния до кораблей в море
Как найти расстояние от точки А, находящейся на берегу до корабля?
Первый способ. Пусть корабль находится в точке K, а наблюдатель в точке A (Приложение 1 рисунок 3). Требуется определить расстояние KA. Построив в точке A прямой угол, необходимо отложить на берегу два равных отрезка AB = BC. В точке C вновь построить прямой угол, причем наблюдатель должен идти по перпендикуляру до тех пор, пока не дойдет до точки D, из которой корабль K и точка B были бы видны лежащими на одной прямой. Прямоугольные треугольники BCD и BAK равны, следовательно, CD = AK , а отрезок CD можно непосредственно измерить.
Второй способ, получивший название метода триангуляции, нашел применение в астрономии. С его помощью измерялись расстояния до небесных тел.
Этот метод состоит из 3-х этапов (Приложение 1 рисунок 4):
1. Измерение углов 1 и 2 и расстояния AB.
2. Построение треугольника А1В1К1 с углами 1 и 2 при вершинах А1 и В1 соответственно.
3. Учитывая подобие треугольников АВК и А1В1К1 составим пропорцию
AK : AB = A1K1 : A1B1, отсюда получим длину отрезка AK
AK = 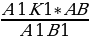
2.8. Измерение школы различными способами
В качестве объекта для измерения высоты я выбрала школу и измерила её тремя наиболее интересными и простыми, на мой взгляд, способами: с помощью равнобедренного треугольника, с помощью зеркала и с помощью высотомера лесника. Предварительно я изготовила «равнобедренный треугольник», высотомер лесника, запаслась зеркалом и рулеткой (Приложение 3 слайд 6).
Измерение с помощью зеркала
Перемещая зеркало, я нашла место, в котором в зеркале был виден фронтон здания (Приложение 3 слайд 7). Измерения показали, что расстояние от зеркала до школы равно 534см, расстояние от меня до зеркала равно 107 см, расстояние от уровня моих глаз до земли равно 160 см. Значит, высоту школы получим из пропорции:
534 : 107 = AB : 160 , отсюда 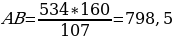
Высота здания равна 798,5 см = 7,985 м
Измерение с помощью равнобедренного треугольника
Отдаляясь от школы, я нашла такое место, в котором продолжение гипотенузы EF совпадало с «вершиной» здания (Приложение 3 слайд 8). На снегу остались мои следы. С помощью рулетки я измерила расстояние от моего местоположения до школы. Получилось BE = 645 см. Прибавив расстояние от уровня моих глаз до земли (160 см) получила, что высота здания OC = 805 см = 8,05 м.
Измерение с помощью высотомера лесника
Расстояние, на которое я отошла от школы равно 1274 см, ниточка с грузиком оказалась на делении 5 см, ширина дощечки равна 10 см (Приложение 3 слайд 9). Получилась пропорция:
ВС : 5 = 1274 : 10, отсюда ВС = 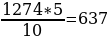 .
.
Для вычисления высоты здания нужно к этому числу прибавить высоту прибора над землей (расстояние от уровня глаз до земли) 637 + 160 = 797.
Высота школы получилась равна 797 см = 7,97 м.
Найдем среднее арифметическое трех измерений
(8,05 + 7,985 + 7,97) / 3 = 8,0016, тогда можно утверждать, что высота школы примерно 8 м. По техническому паспорту школы высота двух этажей составляет 6,23 м, а на чердаке здания спокойно может ходить взрослый человек. Значит, измерения с помощью «подручных средств» дают достаточно точный результат!
3. Геометрия в медицине
3.1. Связь геометрии и медицины
Не зря говорят: математика - царица наук. Числами можно выразить все, что есть в нашем мире! И медицина не исключение. Но какая может быть связь у геометрии с телом человека, если геометрия — раздел математики, изучающий свойства геометрических фигур?
Геометрия играет в анатомии человека очень важную роль: многие элементы тела человека получили свои названия из-за схожести с геометрической фигурой. Например, при классификации суставов человека по форме применялись ассоциации схожести с геометрическими фигурами: цилиндрический, эллипсовидный, шаровидный суставы из самого названия данных суставов уже можно получить представление об их форме. Кроме того, геометрическая терминология присутствует в названиях органов, мышц, костей т.д. Таким образом, в анатомической терминологии фигурирует очень много терминов, связанных с такой наукой, как геометрия.
Большое значение математика имеет в таких медицинских профессиях как врач-статистик, офтальмолог, генетик и т.д. В этих профессиях нужно производить различные расчеты. Практическую значимость имеет расчет веса, объема, площади органов и конечностей. Например, врачи комбустиологи, лечащие ожоги, на основе площади поверхности конечностей при обширных ожогах дают прогнозы и выбирают тактику лечения.
Задачи восстановления картины внутренних органов по их проекциям (медицинская томография) имеет геометрический характер и связана с интегральной геометрией. В медицине применяются геометрические модели различных частей скелета (например, движущейся челюсти при протезировании зубов, коленных и локтевых суставов и др.). Развитие современных 3D технологий сделало возможным создание индивидуальных протезов костей, созданных по результатам 3D сканирования пациента. Также большую роль в современной медицине играют компьютерные модели отдельных органов и их систем. Например, при разработке серьезных операций на сердце часто используется его геометрическая компьютерная модель. Команда ученых из Кэмбриджа (Великобритания) напечатала фрагмент сетчатки глаза, в Принстонском университете (США) из 3D-принтера «вышло» ухо, а в Университете Хуачжун (Китай) при помощи трехмерного печатного устройства воссоздали почку, Российская компания 3D Bioprinting Solutions напечатала щитовидную железу мыши, а к 2020 г. планирует научиться печатать печень.
Измерение конечностей, внутренних органов и тела нужно, чтобы: изготовить протез поврежденных конечностей или внутренних органов; выявить повреждения или болезни, такие как поликистоз почек (увеличение почек и кист), переломы, вывихи, растяжения (деформация), составить правильный рацион питания (что немаловажно для ЗОЖ: рост, вес, возраст).
Кстати, протезированием люди начали заниматься очень давно. Римский ученый, писатель и друг императора - Плиний Старший (примерно 23 - 79 год до н.э.) в своих трудах фиксирует факт о том, что римский генерал Марк Сергий имел металлическую руку, которой держал щит в бою. Наемник и поэт Берлихинген (1480 - 1562) носил протезы обеих рук, сделанные в начале 16-го века. Посмотрите внимательно на его протезы (Приложение 3 слайд 10). Они составлены из геометрических тел!
Еще я узнала, что врачи при расчете дозы лекарства считают показатель поверхности тела наиболее точным по сравнению с массой тела!
Увидев такую тесную связь геометрии с анатомией, я решила попробовать использовать геометрические формулы для вычисления параметров тела человека и сравнить их с показателями из медицинских справочников, построенных на среднестатистических данных.
3.2. Измерение площади верхней конечности (руки)
Представим руку в виде нескольких объемных геометрических фигур: цилиндров, усеченного конуса и семиугольной призмы (Приложение 3 слайд 10). Размеры своей руки я занесла в таблицу (Приложение 1 таблица 1):
Для дальнейших расчетов я воспользовалась следующими формулами:
Площадь боковой поверхности цилиндра S = 2πrh, где
π - число «пи», берем равное 3,14;
r - радиус основания;
h - высота цилиндра.
Площадь боковой поверхности усеченного конуса S= π(r1 + r2)l, где
π - число «пи», = 3,14;
r1 и r2 - радиусы оснований;
l - образующая конуса.
Площадь семиугольной призмы S = 2S1+S2+S3+S4+S5 где
S1-площадь основания; S2, S3, S4, S5-площади боковых граней.
Я рассчитала площадь моей руки и занесла данные в таблицу (Приложение 1 таблица 2).
Согласно медицинским справочникам верхняя конечность (рука) составляет примерно 9% от площади поверхности тела человека. В медицине это «правило девяток» - метод, который используют врачи-комбустиологи для определения площади ожога. При моем росте и весе это приблизительно 1800 см2. В моих вычислениях результат получился немного больше, но, в медицинских расчетах берется среднее значение без учета комплекции человека. Показатели астеника, нормостеника и гиперстеника будут отличаться весьма значительно. Поэтому мои вычисления можно считать верными.
4. Наука психогеометрия
4.1. Геометрия в психологии
Наш характер определяется многими признаками, но оказывается, не остается в стороне и геометрия! Когда мы смотрим на какие-либо предметы, то на подсознательном уровне, сопоставляем их с какими-то геометрическими фигурами и стараемся окружить себя такими же. Существует даже такая наука - психогеометрия. Суть её состоит в исследовании личности. В её основе лежит учение Карла Юнга о психических типах личностей. Однако автором психогеометрии является Сьюзен Деллингер - специалист по социально-психологической подготовке управленческих кадров. Работа С. Деллингер «Психогеометрия: как использовать психогеометрию для воздействия на людей» очень популярна в США. В нашей стране труд С. Деллингер был переработан нашими соотечественниками Анатолием Алексеевым и Ларисой Громовой.
Психогеометрия – это уникальная практическая система анализа личности. Она позволяет мгновенно определить тип личности интересующего вас человека и вашу собственную форму, дать подробную характеристику личностных качеств и особенностей поведения любого человека, составить сценарий поведения для каждой формы личности в типичных ситуациях.
Чтобы определиться в мире психогеометрии, которая как оказалось, влияет на все наши поступки, Деллингер выявила пять психологических типов, каждому из которых соответствует своя геометрическая фигура: квадрат, круг, треугольник, зигзаг, прямоугольник. Каждая фигура имеет свои психологические особенности и по-разному взаимодействует с остальными.
Что ж, заманчиво, не правда ли?
Один из простейших психогеометрических тестов - тест «Геометрические фигуры» (Приложение 2).
4.2. Тестирование школьников
Меня заинтересовал данный тест, связанные с геометрическими фигурами, которые позволяют выявить индивидуально-типологические различия человека. Я провела исследование по изучению особенностей характера обучающихся 5 – 9 классов. В тестировании приняли участие 12 человек. Их ответы я занесла в таблицу (Приложение 2 таблица 1). Я подсчитала все фигуры и занесла результаты в другую таблицу (Приложение 2 таблица 2).
Затем распечатала для каждого обучающегося его характеристику (исходя из выбранной геометрической фигуры) и попросила прочитать. Все обучающиеся «узнали» себя, многие были удивлены, что черты характера, написанные на листочке, совпадают с их чертами! Опрос мнения классных руководителей так же показал, что характеристики подходят обучающимся! Интересно, что никто не выбрал квадрат, но следует отметить, что обучающихся отличающихся особым трудолюбием и усердием в 5-9 классах в нашей школе нет! Значит, данный простой тест вполне можно использовать на практике.
5. Заключение
В результате выполнения данной работы я убедилась, что геометрия нужна современному человеку. Как я и предполагала в начале работы над проектом – геометрия может потребоваться любому человеку. Мы все живем в частных домах. В деревне нет коммунальных служб, поэтому крышу дома или сарая ремонтируют сами жильцы. А, для расчета необходимого количества материала нужно знать площадь крыши. Предпочтительнее в целях безопасности произвести расчеты с поверхности земли. К сожалению, ураганные ветры не обходят Россию стороной. Нередко по телевизору можно услышать, что на жилой дом упало дерево. Но, с помощью простых методов можно рассчитать безопасное расстояние от дома до предполагаемого места посадки дерева!
Я узнала много нового и интересного. Раньше я не могла предположить, что еще до новой эры использовали протезы конечностей, причем успешно! Но, без геометрических знаний было бы не возможно ни современное протезирование, ни медицинская томография, ни печать внутренних органов на 3D-принтере! Неожиданным открытием стало для меня и применение геометрии в психологии!
Я пока не знаю, какую профессию выберу в дальнейшем, но уверена, что знания, полученные в ходе выполнения работы, останутся в моей памяти надолго и помогут мне в дальнейшем. Еще моя работа поможет учителю геометрии показать практическую значимость данного предмета, а, обучающимся поможет понять простую истину:
Без геометрии никакой научный прогресс не возможен!




6. Список литературы
1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. ФГОС Геометрия 7 – 9 классы: Учебник для общеобразовательных организаций. – М.: Просвещение, 2014.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10 – 11 классы: Учебник для общеобразовательных организаций. – М.: Просвещение, 2010.
Электронные ресурсы
1. https://school-science.ru/5/7/34965
2. https://medconfer.com/node/11615
3. https://videouroki.net/razrabotki/material-na-temu-mesto-i-rol-matematiki-v-meditsine.html
4. http://psyholog-praktik.ru/testyi/tipyi-lichnosti-psihogeometriya
5. https://multiurok.ru/files/proiekt-psikhoghieomietriia.html
6. https://psihologiyaotnoshenij.com/stati/psihogeometricheskiy-test-psihogeometriya-kak-nauka-poyavilas-v-ssha-eyo-avtor-styuzen
7. https://nsportal.ru/
8. https://sundekor.ru/kursovaya-2/primenenie-podobiia-na-praktike/
9. http://festival.1september.ru/
10. http://gidproekt.com/kak-rasschitat-ploshhad-krovli-opredelyaem-ploshhad-pokrytiya-krovli-po-formule.html
Приложение 1
Рисунок 1.
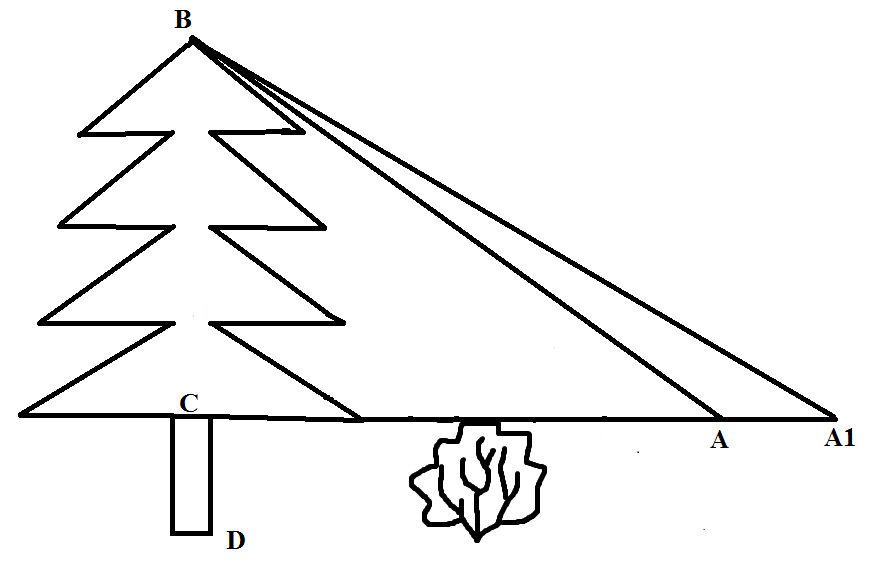
Рисунок 2.
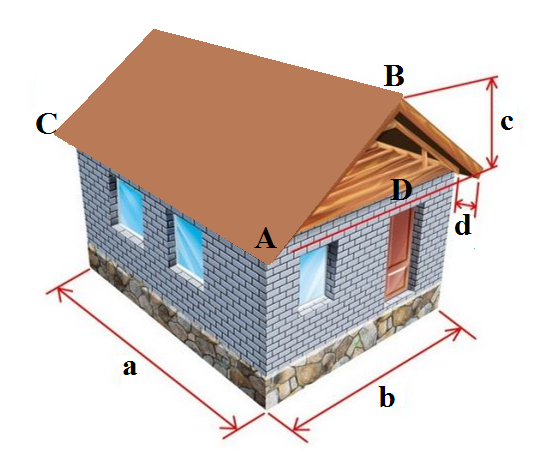
Рисунок 3.
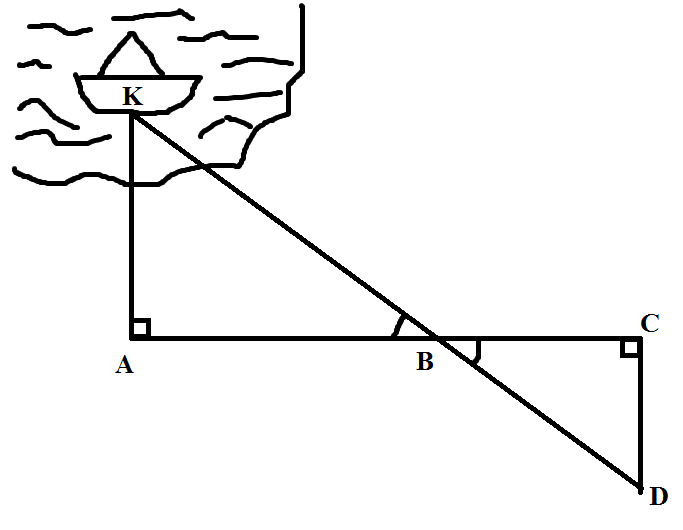
Рисунок 4.
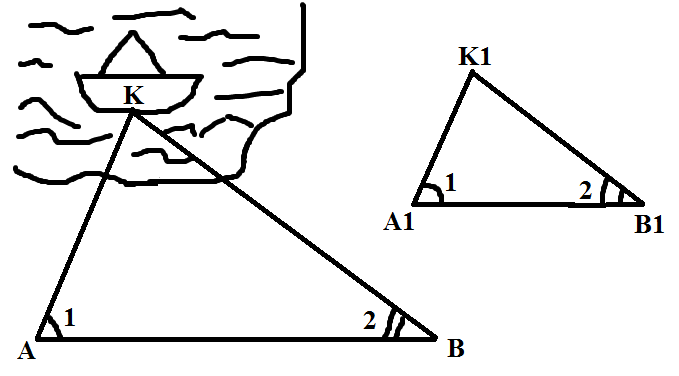
Таблица 1.
| Название части руки | Фигура | Размер, мм |
| Большой палец | Цилиндр | Радиус - 13 Высота - 55 |
| Указательный палец | Цилиндр | Радиус – 12 Высота - 80 |
| Средний палец | Цилиндр | Радиус - 13 Высота - 85 |
| Безымянный палец | Цилиндр | Радиус - 12 Высота - 75 |
| Мизинец | Цилиндр | Радиус - 11 Высота - 60 |
| Ладонь | Семиугольная призма | Площадь основания – 67 Сумма площадей боковых граней – 15 |
| Предплечье | Усеченный конус | Радиус малого основания – 25 Радиус большого основания – 41 Образующая – 260 |
| Плечо | Цилиндр | Радиус –54 Высота – 350 |
Таблица 2.
| Название части руки | Площадь, см2 |
| Большой палец | 44,90 |
| Указательный палец | 60,29 |
| Средний палец | 69,39 |
| Безымянный палец | 56,52 |
| Мизинец | 41,45 |
| Ладонь | 149 |
| Предплечье | 538,82 |
| Плечо | 1186,92 |
| Общая площадь | 2147,29 |
Приложение 2
Психогеометрический тест «Геометрические фигуры».
Инструкция к тесту.
На картинке пять фигур. Выберите ту из них, в отношении которой вы можете сказать: "Вот фигура, символизирующая меня!". Постарайтесь почувствовать ее, сопоставить ее с собой. Если вы испытываете затруднения с выбором фигуры, выберите ту, которая больше всего привлекает вас. Не пытайтесь как-то анализировать характеристики фигур - просто доверьтесь своей интуиции.
Результат выбора:
Квадрат.
Если вами в итоге прохождения психологического теста с геометрическими фигурами выбран квадрат – вы определенно серьезный человек, стабильный и рациональный во всем: и в мыслях, и в поступках. У него главное — здоровье и правильные мысли. Скорее всего, вы уникальный обладатель редкого и похвального качества – стремитесь любое начинание или дело доводить до конца. Главные характеристики такого человека – трудолюбие и усердие. Любителям квадрата присущи такие качества как методичность и терпение, что помогает им достигать хороших результатов в работе и нередко слыть отличными специалистами в своей сфере. Однако их иногда обвиняют в излишней медлительности. А ведь они всего лишь любят все раскладывать по полочкам. Поэтому и перед принятием решения не торопятся, а стремятся лучше изучить сложившуюся ситуацию, собрать дополнительную информацию. Квадраты – это обладатели левополушарного мышления, т.е. сильны в логике, но им легко даются технические специальности. Они скорее «вычисляют результат», чем догадываются о нем, так как чрезвычайно внимательны к деталям и подробностям. Эти неутомимые труженики, как правило, предпочитают распланированную, размеренную жизнь, в которой нет места приключениям спонтанности. Их главная фишка – они постоянно «упорядочивают» людей и вещи вокруг себя. Завоевывать внимание окружающих, используя в своем арсенале рациональность, эмоциональную сухость, консерватизм в оценках квадратам достаточно сложно. В то же время они и не стремятся заявить всем, в том числе и внешне, о своей исключительности и индивидуальности. Нет, они могут ясно излагать свои идеи, но, однако почти никогда не слывут хорошими ораторами, способными увлечь аудиторию. Люди-квадраты говорят, как правило, тихо, предпочитая не повышать голос без надобности. И не терпят повышенных тонов и у других. При этом их речь отличается ясностью, точностью, логичностью и обстоятельностью. Аналитичность мышления утяжеляют их речь, а пристрастие к деталям делают выступление монотонным. Педантичность, скрупулезность и последовательность проявляются и в выборе одежды. Эти люди предпочитают строгий, классический стиль, сдержанные, неяркие тона.
Треугольник.
Те, кто ассоциирует себя с треугольником, безусловно, сильные личности, весьма уверенные в себе и деятельные. Они не любят сидеть на месте, стремятся всегда находиться в гуще событий. Выбор треугольника в качестве основной фигуры может свидетельствовать о развитом честолюбии и власти любой ценой. Они прирожденные лидеры. Нетерпеливость – одна из главных черт их характера. Треугольники могут прервать вас на полуслове, но лишь потому, что уже уловили суть ваших мыслей. Жаждут быть первыми и управлять положением дел, решать не только за себя, но и за других, побеждать конкурентов. Хорошо чувствуют выгоду. Эгоцентричны, но люди тянутся к ним и идут за ними. Для них характерны высокий уровень самооценки, склонность к риску, бьющая через край энергия, высокая работоспособность и тяга к развлечениям. Люди-треугольники весьма контактны и, не испытывая никакого дискомфорта, могут с любым завязать беседу. Отличительные качества – уверенность в себе и стремление быть всегда первыми. Они действительно способны концентрироваться на намеченной цели, быстро анализируют ситуацию и принимают решения. Вместе с тем – не любят признавать свои ошибки и слушать критику. Схватывая все на лету, они быстро учатся. Правда, только тому, что с их точки зрения способствует достижению главной цели. Часто стремятся сделать карьеру. Основной недостаток – эгоцентричность. Это тоже «левополушарные» люди, т.е. те, кто перерабатывает данные в последовательном формате (а-б-в-г…). Способны глубоко и быстро анализировать ситуации, сосредоточившись на главной сути проблемы. Они хотят быть правыми во всём. Готовы постоянно соперничать и конкурировать с другими. «Видят то, что хотят видеть» – это к ним относится в полной мере. Из треугольников получаются отличные управленцы. Главная фишка этого типа людей – создание имиджа. Они стремятся одеваться модно, но не вызывающе, качественно, элегантно и дорого.
Прямоугольник.
Прямоугольник – это переходная фигура. Можно сказать, что это временная форма личности. Прямоугольники не удовлетворены тем образом жизни, который они ведут сейчас, и поэтому заняты поисками лучшего положения. Поэтому люди, которые себя ассоциируют с прямоугольником, часто бывают недовольны собой, всегда хотят большего и лучшего, и почти никогда не бывают удовлетворены. Они часто испытывают замешательство, запутываются в проблемах, с трудом принимают решения. Непоследовательны, совершают непредсказуемые поступки, часто обладают низкой самооценкой. Однако они любознательны, ко многому проявляют интерес. Смелые, охотно берутся за все новое, даже за то, чего никогда раньше не делали. Изменения для них самое важное. Потому что они стремятся стать лучше, ищут новые методы работы, стили жизни. Открыты для новых идей, ценностей, способов мышления и жизни. Стадия «прямоугольника» рано или поздно проходит. Так что вполне возможно, что следующий раз, проходя аналогичный психологический тест с геометрическими фигурами, вы предпочтете другую геометрию.
Круг.
Круг, как известно, символ гармонии. Для этих людей на первом плане будут именно хорошие межличностные отношения. Они любят людей и многое делают для их благополучия. Поэтому часто на них держится и коллектив на работе, и семья. Круг — прирожденный психолог. Можно сказать, что такие люди обладают мягким характером, проявления которого усиливаются умением сгладить острые углы в отношениях. Нельзя сказать, что они в принципе, избегают конфликтов, нет, они просто умеют найти конструктивное решение проблемы. Они ищут свой путь к силе и здоровью. Обладают большой способностью к сочувствию и сопереживанию. Главная ценность для них — люди. Они обладают высокой чувствительностью, развитой эмпатией (способностью сопереживать). Человек-круг прекрасный слушатель, ему всегда можно «поплакаться в жилетку». Они отличаются меланхоличностью, сентиментальностью и устремленностью в прошлое. Хорошо разбираясь в людях, они, тем не менее, на практике, слабые менеджеры и руководители в сфере бизнеса. Все потому, что все их внимание направлено больше на людей, чем на дело. У кругов преобладает правополушарное мышление – творческое, образное. Их мышление образное, интуитивное, эмоционально окрашенное, скорее интегративное, чем анализирующее. Обработка информации осуществляется скорее мозаично, прорывами с пропусками отдельных звеньев. Формализм у них не получает приоритет в решении жизненных проблем. Но кругам, в принципе, не столь уж важно, в чьих руках находится власть. Те, кто выбрал круг сторонятся ответственности, предпочитая ее перекладывать на других. Боясь испортить отношения, не умеют отказывать, дают расплывчатые обещания. Отличаясь нерешительностью, они в плане руководства позволяют брать верх тем же треугольникам. Твёрдость они проявляют лишь в случаях, когда дело касается морали или нарушения справедливости. Предпочитают неофициальный стиль одежды.
Зигзаг.
Любители зигзагов – творческие люди и мыслят они образно. Правда, часто не обращают внимания на детали, воспринимают происходящее целиком. Это позволяет им «видеть» гармонию и целостные образы, по-своему воспринимать красоту. Эти люди любители разнообразия, поэтому обычно не задерживаются долго на одном рабочем месте, часто меняют работу. Устремленные в будущее, они часто забывают о реальности. Обычно зигзаг выбирают «правополушарные» люди. Их мышление построено на интуиции, часто эмоционально окрашено. Им характерна резкая смена настроения. В тоже время зигзаг – это генератор идей, сама креативность и творчество. Однако им трудно работать в хорошо структурированных ситуациях. Их раздражают строго фиксированные обязанности и постоянство. В работе им требуется независимость и высокий уровень мотивации. Зигзаги обычно «правополушарные» люди, то есть они так же не фиксируется на деталях, а строят целостную, гармоничную концепцию картины мира. Могут похвастаться развитым эстетическим чувством. Доминирующим стилем мышления чаще всего является синтетический стиль. Зигзаги решают конфликты путем заострения конфликта идей и построения новой концепции, в которой этот конфликт «снимется». Могут быть довольно язвительными «открывая глаза другим». Главные недостатки зигзагов – они непрактичны и наивны, часто несдержанны, экспрессивны, возбудимы и эксцентричны. Не сильны в проработке конкретных деталей и не слишком настойчивы в доведении дела до конца. Зигзаги нуждаются в высокой стимуляции деятельности. Генерируя идеи в большом количестве, довольно часто отдают их на откуп другим, так как сами не способны довести дело до конца. Не терпят субординацию, любят свободу и независимость, и не поддаются организации, ни в быту, ни в деятельности. Хаос – вот органичное состояние людей-зигзагов. Часто для них с утратой новизны, теряется и интерес к идее. Но их остроумие, веселый нрав и легкость в общении с лихвой компенсируют эти недостатки. Склонны к смешению стилей и небрежности в одежде. Могут появиться в обществе в мятом костюме и чувствовать при этом себя комфортно.
Таблица 1.
| Р.Н. | С.С. | К.Е. | К.Н. | Г.Н. | К.А. | В.П. | С.Д. | Ч.И. | К.М. | Р.В. | М.О. |
| зигзаг | треугольник | треугольник | зигзаг | зигзаг | зигзаг | треугольник | зигзаг | треугольник | зигзаг | круг | круг |
Таблица 2.
| Квадрат | Прямоугольник | Треугольник | Круг | Зигзаг |
| - | - | 4 обуч. | 2 обуч. | 6 обуч. |
| - | - | 33% | 17% | 50% |






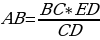
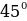 . Следовательно, измерив, расстояние ВE и прибавив OB, т.е. возвышение АЕ глаза над землей, получим искомую высоту дерева.
. Следовательно, измерив, расстояние ВE и прибавив OB, т.е. возвышение АЕ глаза над землей, получим искомую высоту дерева.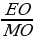 .
.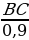 , A1C =
, A1C = 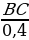 , откуда
, откуда 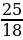 BC отсюда получаем, что BC =
BC отсюда получаем, что BC = 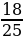 AA1.
AA1.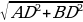 и S = AC ∙ AB
и S = AC ∙ AB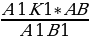
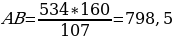
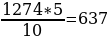 .
.














