Оглавление
| Введение | 3 стр.
|
| Глава 1. Квадратные уравнения и их стандартные способы решения 1.1. В глубину веков | 4 стр. |
| 1.2. Определение квадратного уравнения | 5 стр. |
| 1.2. Стандартные способы решения квадратных уравнений | 6 стр.
|
| Глава 2. Нестандартные способы решения квадратных уравнений |
|
| 2.1. Решение с помощью свойств коэффициентов квадратного уравнения | 7 стр. |
| 2.2. Решение с помощью разложения левой части на множители | 7 стр. |
| 2.3. Решение с помощью выделения полного квадрата | 8 стр. |
| 2.4. Решение методом «переброски» | 8 стр. |
| 2.5. Решение с помощью графического способа | 9 стр. |
| 2.6. Решение с помощью номограммы | 10 стр.
|
| Глава 3. Практическая часть | 12-17 стр.
|
|
|
|
|
| Заключение | 18 стр.
|
| Литература | 18 стр.
|
Приложения 19 стр.
Введение
Великий учёный Михаил Васильевич Ломоносов призывал:
"Старайся дать уму как можно больше пищи..." К этому сегодня стремится каждый, кто хочет занять в современном обществе достойное место, кто хочет быть полезным обществу.
Теория уравнений в школьном курсе алгебры занимает ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Это связано с тем, что большинство жизненных задач сводится к решению различных видов уравнений.
В учебнике алгебры для 8 класса мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем их решение по формулам. У меня возник вопрос: «Существуют ли другие методы решения квадратных уравнений? Насколько сложны данные методы и можно ли ими пользоваться на практике?»
Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения.
Цель работы: исследование разных способов решения квадратных уравнений
Задачи:
-изучить историю развития квадратных уравнений;
-проанализировать стандартные и нестандартные методы решения квадратных уравнений;
-научиться решать квадратные уравнения разными способами.
Гипотеза: существуют интересные и удобные способы решения квадратных уравнений.
Объект исследования: квадратные уравнения.
Предмет исследования: способы решения уравнений второй степени.
Глава 1. Квадратные уравнения и их стандартные способы решения
1.1. В глубину веков
Квадратные уравнения в древнем Вавилоне
Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид - при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
\В математических текстах, выполненных клинописью на глиняных пластинках, есть квадратные и биквадратные уравнения, системы уравнений с двумя неизвестными и даже простейшие кубические уравнения. При этом вавилоняне также не использовали букв, а приводили решение «типовых» задач, из которых решение аналогичных задач получались заменой числовых данных. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются кроме неполных квадратных уравнений и полные уравнения. Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствует понятие отрицательного числа и общее методы решения квадратных уравнений.
Квадратные уравнения у ал-Хорезми
В алгебраическом трактате ал-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений. Основная идея для ал-Хорезми, избегавшего употребления отрицательных чисел, члены каждого из этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал-Джабр и ал-Мукабала. Его решения, конечно, не совпадает полностью с современным решением. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал-Хорезми, как и все математики до XVII века., не учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал-Хорезми на частных числовых примерах излагает правила решения, а затем их геометрические доказательства.
Квадратные уравнения в Европе XIII-XVII вв.
Формулы решения квадратных уравнений по образцу ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202г. итальянским математиком Леонардо Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абака» переходили почти во все европейские учебники XVI-XVII вв. и частично XVIII в.
Квадратные уравнения в ИНДИИ
Задачи на квадратные уравнения встречаются уже в астрономическом трактате «АРИАБХАТТИАМ», составленном в 499 г. индийским математиком и астрономом АРИБХАТТОЙ. Другой индийский ученый, БРАХМАГУПТА (VII век), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме. В уравнении коэффициенты, кроме положительных, могут быть и отрицательными. Правило БРАХМАГУПТЫ по существу совпадает с современным решением. В древней ИНДИИ были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких 5 соревнований следующие: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи».
1.2. Определение квадратного уравнения
Квадратным уравнением называется уравнение вида 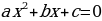 , причем, а ≠ 0, a, b, c - фиксированные действительные числа, которые задают квадратное уравнение. Эти числа имеют определенные названия: a - старший коэффициент (множитель при х2); b - второй коэффициент (множитель при х); c - свободный член (число без множителя-переменной).
, причем, а ≠ 0, a, b, c - фиксированные действительные числа, которые задают квадратное уравнение. Эти числа имеют определенные названия: a - старший коэффициент (множитель при х2); b - второй коэффициент (множитель при х); c - свободный член (число без множителя-переменной).
Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых, т.е. коэффициенты b и с отличны от нуля.
Например: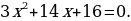
Неполное квадратное уравнение — это уравнение, где в квадратном уравнении 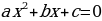 хотя бы один из коэффициентов b или с равен нулю.
хотя бы один из коэффициентов b или с равен нулю.
Существует три вида неполных квадратных уравнений:
1) при 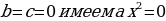 ;
;
2) при 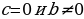 имеем
имеем 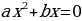 ;
;
3) при 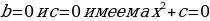 .
.
Например: 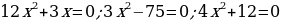 .
.
Квадратное уравнение, в котором коэффициент при х2 равен 1, называют приведенным квадратным уравнением.
Например: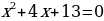 .
.
1.2. Стандартные способы решения квадратных уравнений
1. С помощью формулы.
Дискриминант квадратного уравнения — это выражение, которое находится под корнем в формуле нахождения корней квадратного уравнения. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D. Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней. Для поиска дискриминанта используют формулу: b2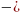 4ac.
4ac.
Для нахождения корней используют нижеизложенную формулу:
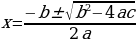 .
.
Возможные случаи в зависимости от значения D:
Если D 0, то уравнение имеет два корня.
Если D = 0, то уравнение имеет один корень: х = 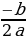 .
.
Если D 0, то уравнение не имеет корней.
2. С помощью следствия теоремы Виета.
Теорема Виета.
Сумма корней приведённого квадратного уравнения 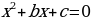 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е.
равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е.

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Глава 2. Нестандартные способы решения квадратных
уравнений
2.1. Решение с помощью свойств коэффициентов квадратного уравнения.
Свойства коэффициентов квадратного уравнения – это такой способ решения квадратных уравнений, который поможет быстро и устно найти корни уравнения.
1. Если в уравнении  коэффициенты
коэффициенты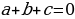 , то его корни равны:
, то его корни равны:  .
.
Например: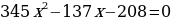 .
.
Решение: т.к. по свойству коэффициентов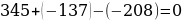 , то корни уравнения будут являться:
, то корни уравнения будут являться:  ;
; 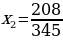 .
.
2. Если в уравнении 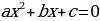 ,
, 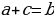 , то корни уравнения будут равны:
, то корни уравнения будут равны: 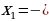 1,
1,  .
.
Например: 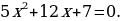
Решение: т.к. по свойству коэффициентов 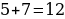 , то корни уравнения будут являться:
, то корни уравнения будут являться: 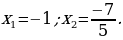
Алгоритм понятен, далее приведу просто сами свойства.
3. Если в уравнения  коэффициенты
коэффициенты 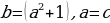 , то корни уравнения будут равны:
, то корни уравнения будут равны: 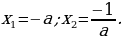
4. Если в уравнении  коэффициенты
коэффициенты 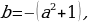
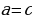 , то корни уравнения будут равны:
, то корни уравнения будут равны: 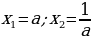 .
.
5. Если в уравнении  коэффициенты
коэффициенты 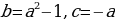 , то корни уравнения будут равны:
, то корни уравнения будут равны: 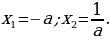
6. Если в уравнении  коэффициенты
коэффициенты 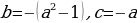 , то корни уравнения будут равны:
, то корни уравнения будут равны: 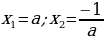 .
.
2.2. Решение с помощью разложения левой части на множители.
Решим уравнение 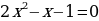 . Разложим левую часть на множители (коэффициент «b» разложить на два числа так, чтобы при их сложении или вычитании получилось прежнее число) и решим уравнение:
. Разложим левую часть на множители (коэффициент «b» разложить на два числа так, чтобы при их сложении или вычитании получилось прежнее число) и решим уравнение:
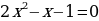 ,
,
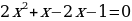 ,
,
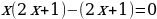 ,
,
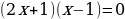 .
.
Следовательно, уравнение можно переписать так: 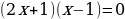 .. Запишем это в виде совокупности и решим:
.. Запишем это в виде совокупности и решим:
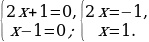
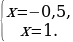
Это означает, что числа -0,5 или 1 являются корнями вышеизложенного квадратного уравнения.
Ответ; 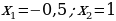 .
.
2.3. Решение с помощью выделения полного квадрата.
Решим уравнение 
Заметим, что 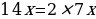 и в выражении
и в выражении 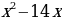 не хватает слагаемого 72, чтобы записать квадрат разности
не хватает слагаемого 72, чтобы записать квадрат разности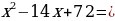 . Тогда к исходному квадратному уравнению добавим
. Тогда к исходному квадратному уравнению добавим 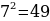 , и, чтобы получить равное выражение, отнимем 49, после чего выделим квадрат разности
, и, чтобы получить равное выражение, отнимем 49, после чего выделим квадрат разности  и суммируем оставшиеся подобные слагаемые:
и суммируем оставшиеся подобные слагаемые:
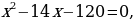
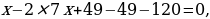
 .
.
Далее перенесём вправо полученный квадрат разности и найдём корни, решив как обычное квадратное уравнение.
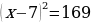 .
.
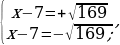
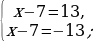
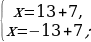

Таким образом мы нашли корни квадратного уравнения с помощью этого способа решения.
Ответ: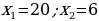 .
.
2.4. Решение методом «переброски».
Рассмотрим метод, который позволяет решать подавляющее большинство полных квадратных уравнений устно, аналогично решению приведенных квадратных уравнений с помощью теоремы Виета.
Рассмотрим полное квадратное уравнение: 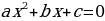 .
.
Теперь рассмотрим другое полное приведённое квадратное уравнение: 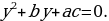
Первый коэффициент у этого уравнения равен 1, а второй коэффициент равен 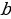 и совпадает со вторым коэффициентом уравнения. Свободный член уравнения равен
и совпадает со вторым коэффициентом уравнения. Свободный член уравнения равен 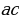 и получен как произведение первого коэффициента и свободного члена уравнения (т.е. можно сказать, что a «перебросилось» к «
и получен как произведение первого коэффициента и свободного члена уравнения (т.е. можно сказать, что a «перебросилось» к «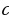 »). «
»). «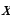 » меняется на «
» меняется на «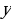 » (желательно для того, чтобы не запутаться дальше).
» (желательно для того, чтобы не запутаться дальше).
А теперь момент, про который многие забывают при использовании этого метода решения квадратных уравнений: в полученном уравнении можно найти корни через теорему Виета или через дискриминант, но они не являются решением. Необходимо их поделить на коэффициент 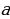 , на который мы умножали свободный коэффициент квадратного уравнения, при этом у нас возвращается
, на который мы умножали свободный коэффициент квадратного уравнения, при этом у нас возвращается 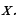
Рассмотрим это на примере:
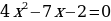 ;
;
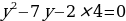 ,
,
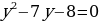 .
.
Находим корни через теорему Виета или через дискриминант:
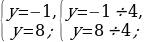
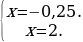
Так мы нашли корни уравнения с помощью этого способа решения.
Ответ: 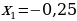 ;
; 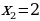 .
.
2.5 Решение с помощью графического способа.
Графических способов много, но многие их них очень сложны, поэтому мы рассмотрим только один способ, способ перенесения 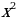 .
.
График первой зависимости – парабола, проходящая через начало координат. График второй зависимости – прямая. Из полученных графиков ищем точки пересечения графиков, которые и будут являться корнями нашего квадратного уравнения.
Рассмотрим пример: 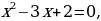
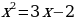 .
.
Теперь мы можем обе части подставить к 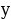 , у нас получится два графика. Графики на одном чертеже будут выглядеть примерно так:
, у нас получится два графика. Графики на одном чертеже будут выглядеть примерно так:
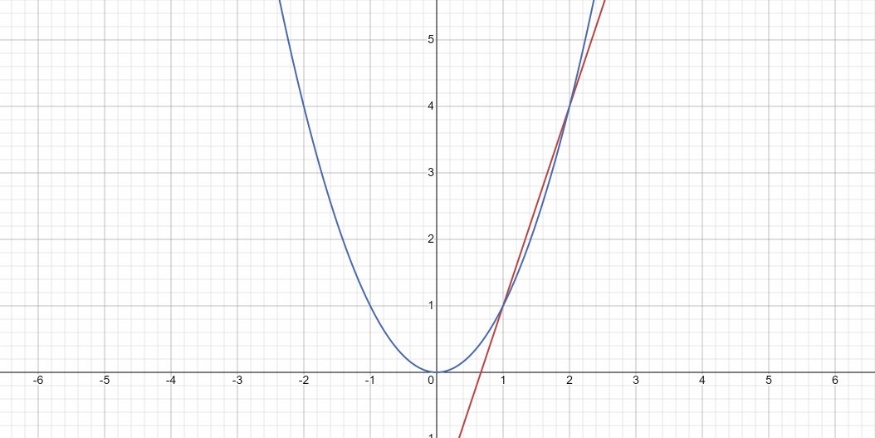
Можно увидеть, что точки пересечения – это 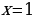 и
и 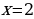 . Это и будут корни уравнения.
. Это и будут корни уравнения.
Ответ:  ;
; 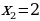 .
.
Но нужно понимать, что способ не всегда эффективен, так как могут получиться некрасивые корни. Советую использовать его тогда, когда перед нами приведённое уравнение с не очень большими цифрами
2.6. Решение с помощью номограммы
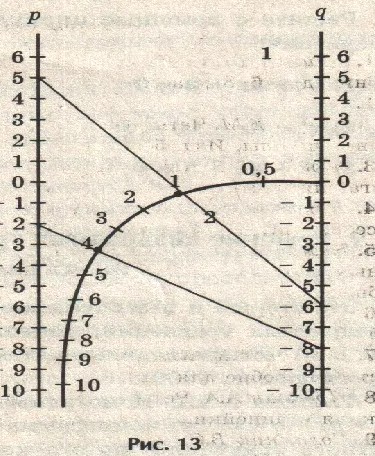 Это старый и незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990). Он доволен сложен в самом изучении
Это старый и незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990). Он доволен сложен в самом изучении
Номограмма для решения уравнения  . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
 Полагая, что ОС = р, ED = q, ОЕ = а из подобия треугольников САН и CDF получим пропорцию, откуда после подстановок и упрощений вытекает уравнение:
Полагая, что ОС = р, ED = q, ОЕ = а из подобия треугольников САН и CDF получим пропорцию, откуда после подстановок и упрощений вытекает уравнение:
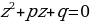 .
.
Причём буква 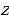 означает метку любой точки криволинейной шкалы.
означает метку любой точки криволинейной шкалы.
Рассмотрим примеры для решения квадратного
1. Когда две точки.
Для примера рассмотрим следующие квадратные уравнения:
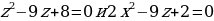 .
.
C помощью данной номограммы можно понять, что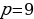 ,
, 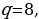 следовательно, соединяя точки, можно понять, что у первого уравнения точки будут
следовательно, соединяя точки, можно понять, что у первого уравнения точки будут 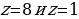 . Это и будет являться решением вышеизложенного квадратного уравнения.
. Это и будет являться решением вышеизложенного квадратного уравнения.
Ответ: 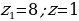 .
.
В случае со вторым уравнением, то для начала его нужно сделать приведённым, разделив коэффициенты на 2. Получим уравнение: 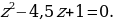
C помощью номограммы таким же методом решения, что и в первом, можно понять, что у второго уравнения точки будут 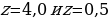 .
.
Ответ: 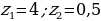
2. Если одна точка.
В данном случае номограмма даст положительный корень, поэтому нужно теперь найти отрицательный корень.
Для нахождения этого отрицательного корня необходимо будет воспользоваться формулой:  .
.
Первое уравнение: 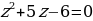 .
.
Номограмма даёт точку 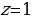 . Это и будет первый корень.
. Это и будет первый корень.
Находим второй корень: 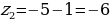 .
.
Ответ: 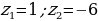 .
.
Второе уравнение: 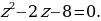
Номограмма даёт точку 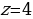 . Это и будет первый корень квадратного уравнения.
. Это и будет первый корень квадратного уравнения.
Находим второй корень: 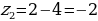 .
.
Ответ: 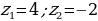 .
.
Нужно подметить, что когда этот способ стал для меня известен, то я не понимала, почему таблица представлена именно полукругом. Этот способ действующий, но над ним необходимо будет ещё поработать, что я сделаю в дальнейшем.
Глава 3. Практическая часть
3.1. Решение квадратного уравнения всеми известными мне способами
В своей практической части я поставила себе задачу разобрать решение одного квадратного уравнения всеми мне известными способами и сделать вывод о плюсах и минусах каждого из сособов решения. А так же выбрать для себя самый рациональный метод решения, который позволит мне в дальнейшем успешно решать задачи разного типа.
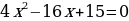
| 1 способ. Разложение левой части уравнения на множители. 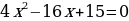 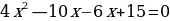 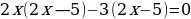 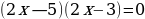  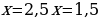 | 2. Метод выделения полного квадрата 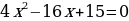 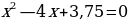 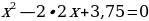 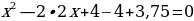 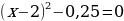 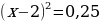 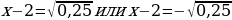 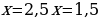 |
| 3.Решение квадратных уравнений по формуле а) 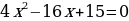 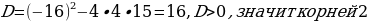 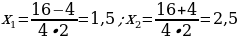 б) так как b четное число и k=-8
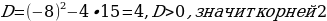 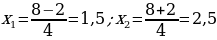 | 4. Решение уравнений с использованием теоремы Виета 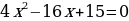  q=3,750 ,имеет два одинаковых по знаку корня p=-4оба корня положительные 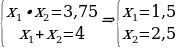 |
| 5. Решение уравнений способом «переброски» 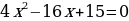  по Виету 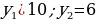 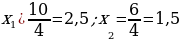 | 6. Свойство коэффициентов квадратного уравнения a+b+c=0 4 + (-16) + 15 ≠ 0 a+c=d 4 + 15 ≠ 16 данный способ не подходит |
| 7.Графическое решение квадратных уравнений 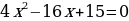 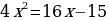 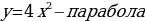 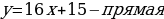 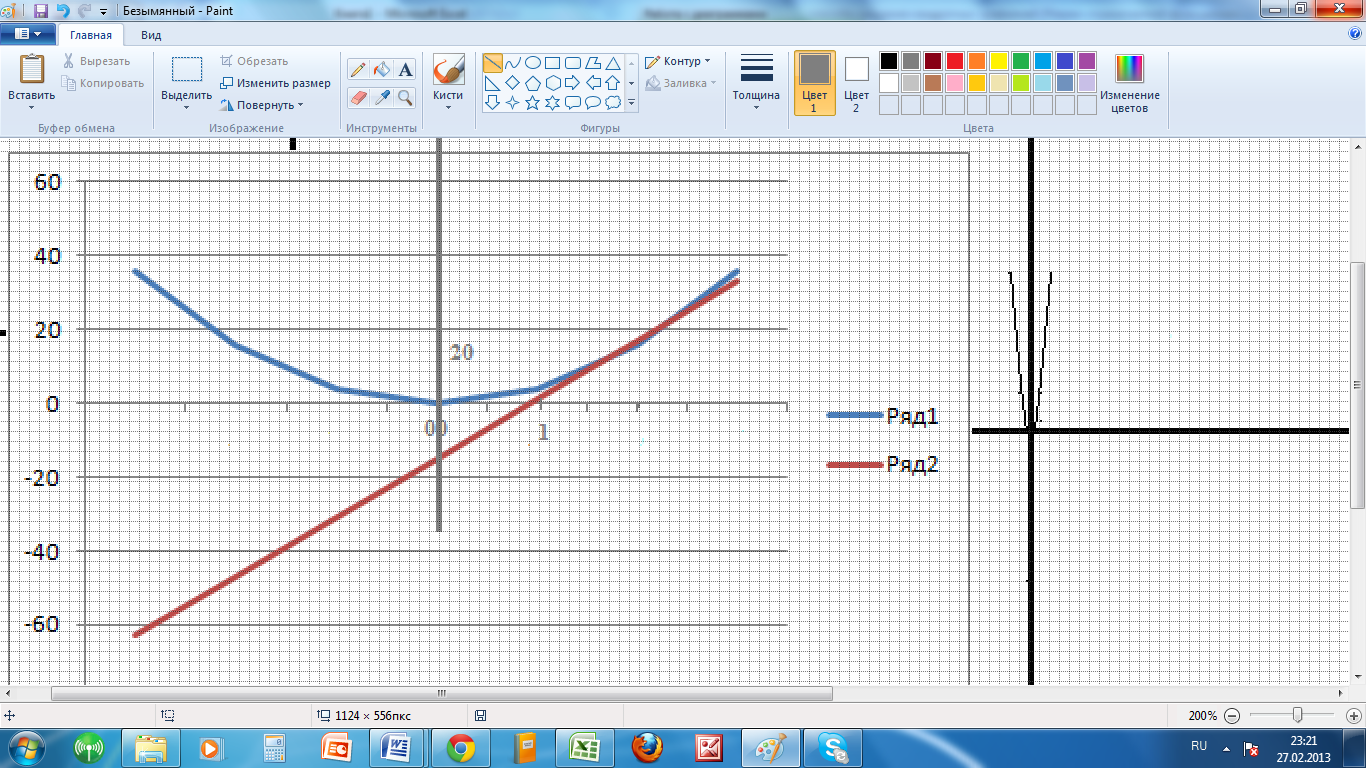
| 9. Решение квадратных уравнений с помощью номограммы 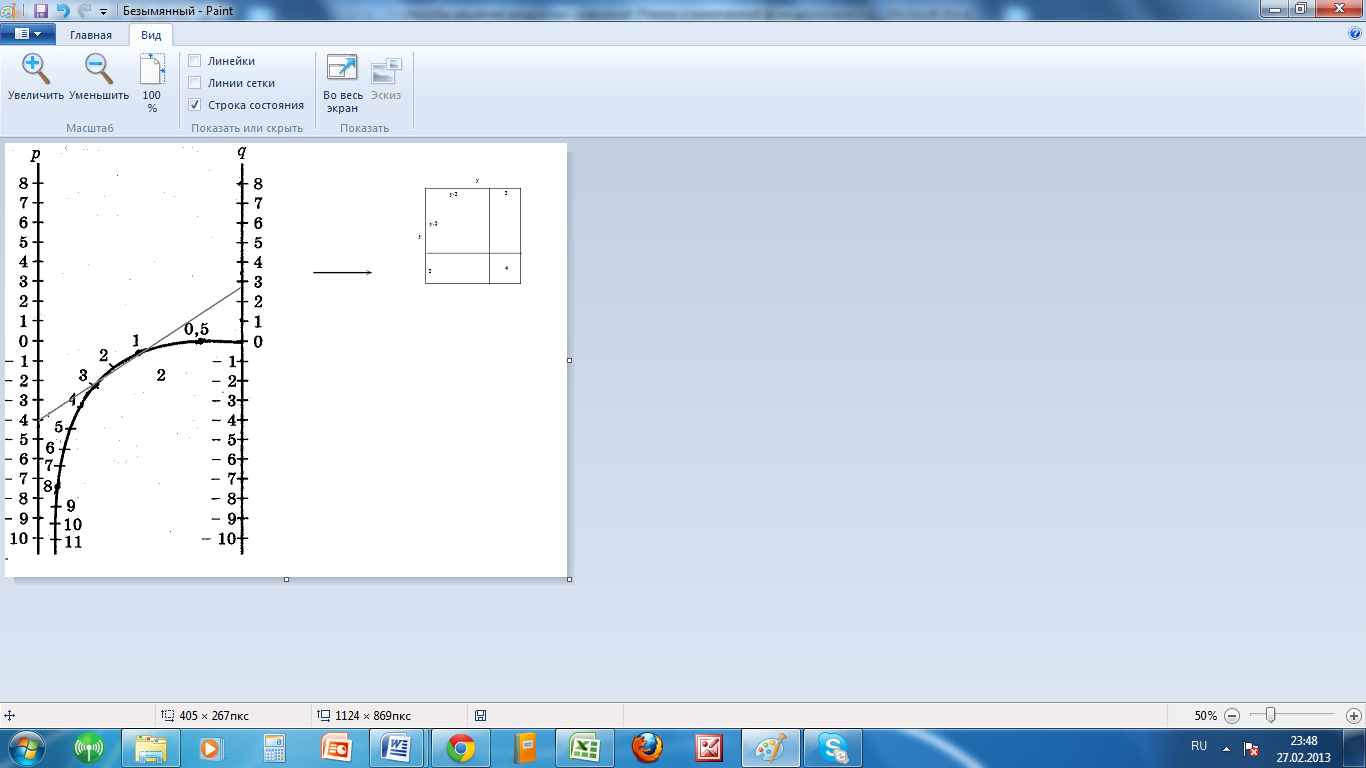 |
Вывод:
Решая квадратные уравнения, я поняла, что любое квадратное уравнение не возможно решить с помощью всех способов. Для того, чтобы уметь решать уравнение любым способом, ученику придется запомнить всю теорию, связанную со способом решения квадратных уравнений. Но запоминание всех способов не даст хорошего результата, так как, исследуя все способы решения, я выяснила, что самый эффективный способ нахождения корней уравнений -это способ решения квадратных уравнений по формуле. Легко запоминаются формулы для вычисления корней и дискриминанта, да к тому же имеются всего лишь 3 свойства дискриминанта, которые легко запомнить. Только этот способ дал мне возможность решить любое квадратное уравнение.
Но, не смотря на это, у каждого способа есть свои положительные и интересные стороны. Каждый способ имеет свои «плюсы» и «минусы», которые я занесла в таблицу.
| Название способа решения квадратных уравнений | Плюсы | Минусы |
| Разложение левой части уравнения на множители | Дает возможность сразу увидеть корни уравнения. | Нужно правильно найти слагаемые для группировки. |
| Метод выделения полного квадрата | За минимальное количество действий можно найти корни уравнений | Нужно правильно найти все слагаемые для выделения полного квадрата. |
| Решение квадратных уравнений по формуле | Можно применить ко всем квадратным уравнениям. | Нужно выучить формулы.
|
| Решение уравнений с использованием теоремы Виета | Достаточно легкий способ, дает возможность сразу увидеть корни уравнения. | Легко находятся только целые корни. |
| Решение уравнений способом переброски | За минимальное количество действий можно найти корни уравнения, применяется совместно со способом теоремы Виета. | Легко найти только целые корни. |
| Свойства коэффициентов квадратного уравнения | Не требует особых усилий | Подходит только к определенному типу уравнений |
| Графическое решение квадратного уравнения | Наглядный способ | Могут быть не точности при построении графиков |
| Решение квадратных уравнений с помощью номограммы | Наглядный способ, прост в применении. | Не всегда под рукой имеется номограмма. |
3.2 Эксперимент с одноклассниками
После изучения различных способов решения квадратного уравнения я предложила десяти своим одноклассникам решить несколько уравнений. Мне было интересно: каким способом они будут пользоваться? Для решения я предложила им следующие уравнения:
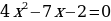 ,
,
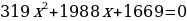 ,
,
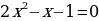 ,
,
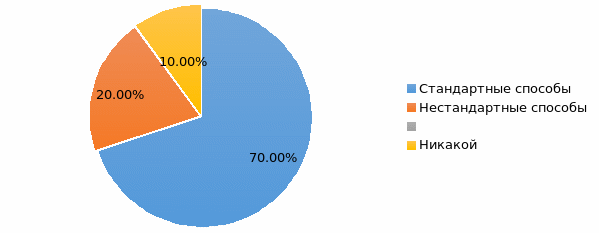 В ходе проведенного эксперимента я получила следующие результаты:
В ходе проведенного эксперимента я получила следующие результаты:
По данной полученной диаграмме можно сделать такие выводы:
-больше всего учеников (70%) решили воспользоваться формулой дискриминанта;
-20 % знали нестандартные способы решения.
Но были также и такие ученики, которые ничего и не решили вовсе (10%), что очень расстраивает.
3.3 Материал к занятию по теме «Решение квадратных уравнений способом «переброски»
Тема: «Решение квадратных уравнений способом «переброски»
Цель: Научить одноклассников решать квадратные уравнения нестандартным способом.
Это интересно. Биографическая миниатюра. Ф. Виет.
Формулы решения квадратных уравнений в Европе были впервые написаны в 1202 году. Вывод формулы решения квадратного уравнения встречается у французского математика Ф. Виета. Франсуа Виет родился в провинции Франции в 1540 году. Виет имел возможность получить хорошее образование и относился к обучению очень серьезно. Став юристом, он продолжал заниматься математикой, астрономией и космологией. В 1591 году Виет ввел буквенные обозначения не только для неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало впервые возможным выражение свойств уравнений и их корней формулами. Среди открытий сам Виет особенно высоко ценил установление зависимости между корнями и коэффициентами уравнений.
По праву достойна в стихах быть воспета.
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого,
Умножишь ты корни – и дробь уж готова.
В числителе С, в знаменателе А.
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда?
В числителе В, в знаменателе А.
А все могло быть по-другому. Эта замечательная теорема могла быть открыта совсем другим талантливым человеком. А знаете почему?
Испанские инквизиторы изобрели очень сложную тайнопись (шифр), которая все время изменялась и дополнялась. Благодаря этому шифру воинствующая и сильная в то время Испания могла свободно переписываться с противниками французского короля даже внутри Франции, и эта переписка оставалась неразгаданной. После бесплодных попыток найти ключ к шифру король обратился к Виету. Известно, что Виет, две недели подряд дни и ночи просидев за работой, все же нашел ключ к испанскому шифру. После этого неожиданно для испанцев Франция стала выигрывать одно сражение за другим. Испанцы долго недоумевали. Наконец им стало известно, что шифр для французов уже не секрет и что виновник его расшифровки – Виет. Будучи уверенными, в невозможности разгадать способ тайнописи людьми, они обвинили Францию перед Папой Римским и инквизицией в кознях дьявола, а Виета обвинили, что он был в союзе с дьяволом и приговорили его к сожжению на костре. К счастью для науки, он не был выдан инквизиции.
Изучение способа «переброски».
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2 х2 + а bх + ас = 0.
Пусть ах = у, откуда х = 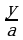 ; тогда приходим к уравнению
; тогда приходим к уравнению
у2 + by + ас = 0,
равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = 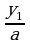 и х1 =
и х1 = 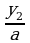 . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену и решим уравнение по теореме Виета: у2-11у+30=0
Согласно теореме Виета х1=  ; х2=
; х2=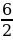 =3
=3
Пример 2 (один ученик решает на доске, остальные в тетрадях)
2х2 – 9х + 9 = 0
Решение:
у2 – 9у + 18 = 0
у1 = 6 х1 = 6/2 х1 = 3
у2 = 3 ↔ х2 = 3/2 ↔ х2 = 1,5
Ответ: 3; 1,5.
«Математическая эстафета». Работа по командам. На последней парте каждого ряда находится листок с 6 заданиями (по 2 задания на каждую парту). Ученики, получившие листок, выполняют первые 2 задания (разрешается совместная работа) и передают листок впереди сидящим ребятам.
Решите уравнения, используя метод «переброски»:
10х2 – 11х + 3 = 0 3. 3х2 + 11х + 6 = 0 5. 6х2 + 5х – 6 = 0
2х2 + х – 10 = 0 4. 5х2 – 11х + 6 = 0 6. 4х2 + 12х + 5 = 0
Работа считается оконченной, когда организатор получает три листка (по количеству рядов) с выполненными 6 заданиями.
Побеждают учащиеся того ряда, в котором раньше решат шесть примеров.
Проверка итогов работы осуществляется с помощью мультимедийного проектора.
Заключение
Человечество прошло длинный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание всё более полным и совершенным.
Уравнения – язык алгебры, квадратные уравнения – это фундамент, на котором построено величественное здание алгебры. Изученные способы решения квадратных уравнений будут применяться и при дальнейшем изучении математики, при решении уравнений, сводящихся к решению квадратных.
В ходе выполнения работы с поставленной целью и задачами я справилась, мне удалось обобщить и систематизировать изученный материал по вышеуказанной теме. Проанализировав все новые способы решения квадратных уравнений, я пришла к выводу, что нельзя однозначно сказать, какой именно метод наиболее удобен или совершенен. Некоторые способы удобно применять, когда коэффициенты невелики, другие – допускают большие коэффициенты ( например, учёт коэффициентов), графический не всегда точен, а геометрический понятен, но громоздок. Можно сделать вывод, что все способы надо иметь в своем арсенале и применять их по мере необходимости с точки зрения рациональности решения.
Данная работа помогла мне повторить известные мне способы решения квадратных уравнений, а также познакомиться с новыми, которые не изучают в школьном курсе математики.
Литература
Выгодский М.Я. Справочник по элементарной математике. – М. государственное издательство физико-математической литературы, 1970.
Галицкий М.Л., Гольдман М., Звавич Л.И. Сборник задач по алгебре для 8-9 классов: учебное пособие для учащихся школ и классов с углубленным изучением математики:4-е изд.-М.: Просвещение, 1997.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Учебник для 8 класса. М., Просвещение, 2021.
Макарычев Ю.Н., Миндюк Н.Г. Дополнительные главы к школьному учебнику. 8 класс М., Просвещение, 1996.
Штейнгауз В.Г. Математический калейдоскоп. – М.: Бюро «Квантум», 2005.
Энциклопедический словарь юного математика. – М.: Педагогика, 1985 7. Ресурсы сети Интернет
8. Программы «Advanced Grapher» и «Открытая математика».
Приложение
21







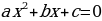 , причем, а ≠ 0, a, b, c - фиксированные действительные числа, которые задают квадратное уравнение. Эти числа имеют определенные названия: a - старший коэффициент (множитель при х2); b - второй коэффициент (множитель при х); c - свободный член (число без множителя-переменной).
, причем, а ≠ 0, a, b, c - фиксированные действительные числа, которые задают квадратное уравнение. Эти числа имеют определенные названия: a - старший коэффициент (множитель при х2); b - второй коэффициент (множитель при х); c - свободный член (число без множителя-переменной).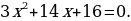
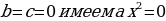 ;
;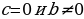 имеем
имеем 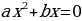 ;
;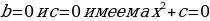 .
.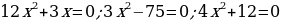 .
.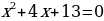 .
. 4ac.
4ac.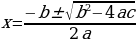 .
.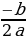 .
.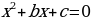 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е.
равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену, т.е.
 коэффициенты
коэффициенты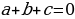 , то его корни равны:
, то его корни равны:  .
.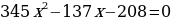 .
.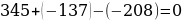 , то корни уравнения будут являться:
, то корни уравнения будут являться:  ;
; 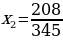 .
.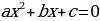 ,
, 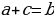 , то корни уравнения будут равны:
, то корни уравнения будут равны: 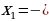 1,
1,  .
.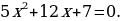
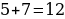 , то корни уравнения будут являться:
, то корни уравнения будут являться: 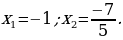
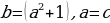 , то корни уравнения будут равны:
, то корни уравнения будут равны: 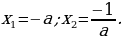
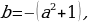
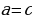 , то корни уравнения будут равны:
, то корни уравнения будут равны: 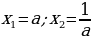 .
.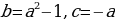 , то корни уравнения будут равны:
, то корни уравнения будут равны: 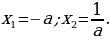
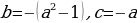 , то корни уравнения будут равны:
, то корни уравнения будут равны: 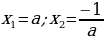 .
.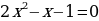 . Разложим левую часть на множители (коэффициент «b» разложить на два числа так, чтобы при их сложении или вычитании получилось прежнее число) и решим уравнение:
. Разложим левую часть на множители (коэффициент «b» разложить на два числа так, чтобы при их сложении или вычитании получилось прежнее число) и решим уравнение: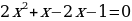 ,
,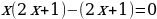 ,
,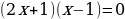 .
. 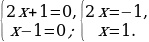
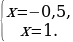
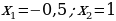 .
.
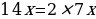 и в выражении
и в выражении 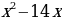 не хватает слагаемого 72, чтобы записать квадрат разности
не хватает слагаемого 72, чтобы записать квадрат разности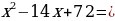 . Тогда к исходному квадратному уравнению добавим
. Тогда к исходному квадратному уравнению добавим 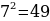 , и, чтобы получить равное выражение, отнимем 49, после чего выделим квадрат разности
, и, чтобы получить равное выражение, отнимем 49, после чего выделим квадрат разности  и суммируем оставшиеся подобные слагаемые:
и суммируем оставшиеся подобные слагаемые: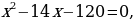
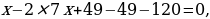
 .
.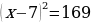 .
.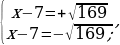
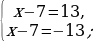
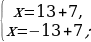

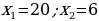 .
.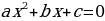 .
.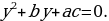
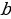 и совпадает со вторым коэффициентом уравнения. Свободный член уравнения равен
и совпадает со вторым коэффициентом уравнения. Свободный член уравнения равен 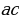 и получен как произведение первого коэффициента и свободного члена уравнения (т.е. можно сказать, что a «перебросилось» к «
и получен как произведение первого коэффициента и свободного члена уравнения (т.е. можно сказать, что a «перебросилось» к «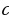 »). «
»). «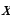 » меняется на «
» меняется на «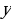 » (желательно для того, чтобы не запутаться дальше).
» (желательно для того, чтобы не запутаться дальше).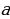 , на который мы умножали свободный коэффициент квадратного уравнения, при этом у нас возвращается
, на который мы умножали свободный коэффициент квадратного уравнения, при этом у нас возвращается 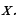
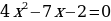 ;
;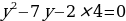 ,
,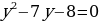 .
.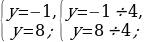
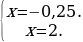
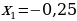 ;
; 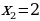 .
.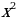 .
.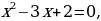
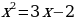 .
. , у нас получится два графика. Графики на одном чертеже будут выглядеть примерно так:
, у нас получится два графика. Графики на одном чертеже будут выглядеть примерно так:
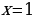 и
и 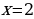 . Это и будут корни уравнения.
. Это и будут корни уравнения. Это старый и незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990). Он доволен сложен в самом изучении
Это старый и незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990). Он доволен сложен в самом изучении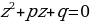 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.  Полагая, что ОС = р, ED = q, ОЕ = а из подобия треугольников САН и CDF получим пропорцию, откуда после подстановок и упрощений вытекает уравнение:
Полагая, что ОС = р, ED = q, ОЕ = а из подобия треугольников САН и CDF получим пропорцию, откуда после подстановок и упрощений вытекает уравнение: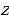 означает метку любой точки криволинейной шкалы.
означает метку любой точки криволинейной шкалы.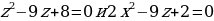 .
.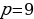 ,
, 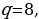 следовательно, соединяя точки, можно понять, что у первого уравнения точки будут
следовательно, соединяя точки, можно понять, что у первого уравнения точки будут 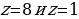 . Это и будет являться решением вышеизложенного квадратного уравнения.
. Это и будет являться решением вышеизложенного квадратного уравнения.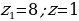 .
.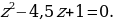
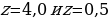 .
.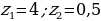
 .
.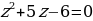 .
.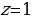 . Это и будет первый корень.
. Это и будет первый корень.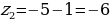 .
.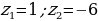 .
.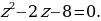
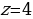 . Это и будет первый корень квадратного уравнения.
. Это и будет первый корень квадратного уравнения. 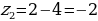 .
.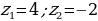 .
.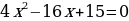
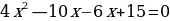
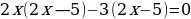
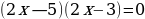

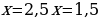
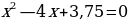
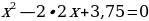
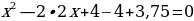
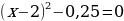
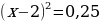
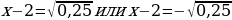
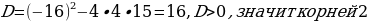
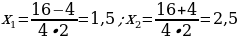
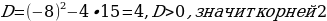
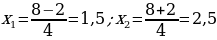

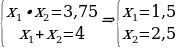

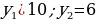
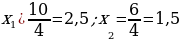
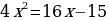
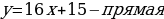


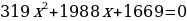 ,
,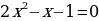 ,
, В ходе проведенного эксперимента я получила следующие результаты:
В ходе проведенного эксперимента я получила следующие результаты: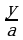 ; тогда приходим к уравнению
; тогда приходим к уравнению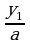 и х1 =
и х1 = 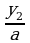 . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат. ; х2=
; х2=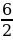 =3
=3









