Индивидуальный итоговый проект Тема: «Теория графов в рамках программы ФГОС»

Муниципальное автономное общеобразовательное учреждение г. Хабаровска

«Лицей инновационных технологий»

Индивидуальный итоговый проект

Тема:

«Теория графов в рамках программы ФГОС»

Выполнила:

Ученица 10 «А» класса

Гайфулина Алия

Руководитель: Дубинская Ирина Александровна

г. Хабаровск-2021

Введение………………………………………………………………………..…3

Написание теоретической части пособия..…………………………....….…….6

Работа над практической частью пособия………………...………...…….........9

Оформление учебно-методического пособия……..……………………..……12

Заключение……………………………………………………………………....14

Источники……………………………………………………………………......15

Приложение……………………………………………………………………...16

Основной пласт знаний, мировоззрение, способность обучаться и контактировать с обществом – всё это детям в немалой степени даёт школа. Здесь, без преувеличения, наравне с семьёй формируется личность ребёнка. Школа призвана развить таланты ученика, познакомить его с миром и его устройством, привить навыки общения и саморазвития. Невероятно важно уделить достаточно внимания каждой науке, каждому предмету, преподаваемому в школе, поскольку никто не может знать, в чём ребёнок заинтересуется и чему он захочет посвятить свою дальнейшую жизнь. Ученики нередко перенимают азарт и вдохновение педагога, запоминают сложные для них факты по интересным задачам или попросту нарабатывают важные в будущем навыки на множестве упражнений разной степени сложности. Сложно переоценить важность обучения, поэтому образование уже долгое время является одной из самых актуальных тем в обществе. Его цели, задачи, проблемы и методы всегда подвергаются критике и непрерывно меняются, поскольку меняется и мир вокруг. Каждый родитель или школьник в какой-то момент своей жизни возмущался, что его учат чему-то не тому и как-то не так. Школьную программу составляют и тщательно прорабатывают лучшие педагоги страны, она проходит множество проверок и однозначно внушает доверие в абсолютном большинстве случаев. Она хорошо раскрывает все базовые темы, но нередко внести в неё какие-либо изменения хотят даже сами учителя.

В чём дело? Ну, как уже было сказано мир вокруг нас меняется непрерывно, меняется востребованность отдельных тем по программе, меняются даже задания на экзаменах. Разумеется, ученики заинтересованы в том, чтобы быть готовыми к любому возможному сценарию. Отдельную речь необходимо вести об углублённом изучении школьных предметов. Год от года в нашей стране развивается олимпиадное движение. Чем раньше дети будут получать возможность приобщаться к олимпиадной подготовке, тем больше у них будет шансов достичь успеха в этом направлении. Особое место здесь занимают олимпиады по техническим предметам и, в частности, математике. Дети принимают в них участие со средней или даже начальной школы, эти олимпиады сильно разнятся по степени сложности, в них существует большая вариативность. Иногда в математике даже происходит так, что какая-то тема считается олимпиадной и не затрагивается в школьном курсе, тогда как на самом деле она уже получила широкое распространение и является весьма востребованной для изучения даже в основной общеобразовательной программе.

Когда так происходит, необходимую тему стараются постепенно вводить в школьную программу. Так, например, на сегодняшний момент уже несколько лет ходят разговоры о включении в школьную программу теории графов на базовом ознакомительном уровне. В школьной математике графам абсолютно не уделяется времени, в то время как они достаточно активно используются в информатике и олимпиадной математике. Графы – один из удобнейших способов представления информации в отдельных случаях, а также незаменимый инструмент рационального решения некоторых задач школьной программы по математике и информатике, не говоря уже об олимпиадном или углублённом уровне изучения.

Итак, в данном проекте я представляю Вашему вниманию процесс по созданию учебно-методического пособия «Теория графов в рамках программы ФГОС», направленному на введение теории графов на базовом уровне в школьную программу и постепенное изучение её школьниками 6-9 классов.

Актуальность моего проекта заключается в том, что на сегодняшний день включение теории графов в школьную программу необходимо, поскольку её использования требуют некоторые распространённые типы задач по математике и информатике. Однако до сих пор тема считается только олимпиадной, поэтому нужно тщательно проработать её включение в школьную программу для общего ознакомления с ней учеников.

Цель: изучить основные положения теории графов и создать учебно-методическое пособие для школьников 6-9 класса.

Для достижения цели мной были поставлены следующие задачи:

• изучить существующие пособия для математических кружков и олимпиадной подготовки;

• подготовить собственную теоретическую часть пособия на основе существующих книг и пособий по данной теме;

• составить подборку задач и упражнений к каждой главе теоретической части;

• при необходимости придумать упражнения нужного формата;

• оформить учебно-методическое пособие по всем правилам его составления.

Работа над теоретической частью моего проекта тоже в свою очередь поделилась на две части: анализ теории, представленной в существующих учебно-методических пособиях для школьников и математических кружков, и написание теоретического минимума к собственному пособию.

Работая с готовыми пособиями, я уделяла особое внимание отдельным книгам. Дело в том, что для введения тем теории графов в школьную программу недостаточно просто определений. Зачастую необходимо объяснение применения теорем, алгоритмов работы или даже способов представления информации. В качестве книги с доступным объяснением, на которую я часто равнялась при наборе текста теоретического минимума в главах моего проекта, была взята книга В. М. Гуровица и В. В. Ховриной «Графы», предназначенная для проведения математических кружков с учениками 6-8 классов. В этой книге даётся тот самый ознакомительный уровень, который и необходим ученикам школы для работы с графами в рамках школьной программы. При написании своего методического пособия я старалась сохранить доступность языка, не теряя точности при описании математических понятий и явлений. Книга «Графы» послужила мне отличным примером в данном вопросе. Помимо неё я активно использовала сайт foxford.ru для поиска определений и понятий. Он особенно пригодился при описании базовых понятий теории графов, которые также связаны с графическим строением самого графа.

Итак, проанализировав доступную теорию, я приступила к написанию теоретической части собственного учебно-методического пособия. Сначала в нём рассматривается применение графа как способа представления информации.

В начале первого раздела постаралась самостоятельно объяснить доступным языком предназначение графов и привести примеры ситуаций, когда использование графов удобно и рационально. Сразу после этого даётся определение графа и общее понятие о нём. В первой главе своего пособия я рассматриваю строение графа, его основные виды. Здесь вводится основная терминология теории графов и коротко говорится о двух больших «семействах» графов: разделяются неориентированные и ориентированные графы. Это важно сделать с самого начала, поскольку ориентированные и неориентированные графа выполняют отличную друг от друга роль при использовании их для решения задач. Основная мысль первой главы – познакомить ученика с графическим изображением ситуации при помощи графа. Во второй главе пособия к вниманию читателя представлено ещё одно важнейшее понятие теории графов, которое лежит в основе всего последующего изучения – степень вершины. Теоретический минимум этой главы рассказывает о степени вершины как её основной характеристике при описании графа и решении многих математических задач. Здесь же впервые формулируется Лемма о рукопожатиях, которая становится первым утверждением пособия, требующим доказательства. Полученные в первой главе знания о терминологии теории графов и применении графа уже активно используются во второй главе, где расширяется наше знание о вершинах и рёбрах как составляющих графа.

Во втором разделе пособия ученик знакомится с определёнными частями графа, состоящими из вершин и рёбер, содержащими их. Здесь вводятся новые определения, которые тоже будут основополагающими в следующих разделах. В первой главе раздела читатель знакомится с понятием связности и определением компоненты связности, во второй – с маршрутом, путём и циклом в пределах графа, а третья глава раздела посвящена изоморфным графам. После изучения данной главы читатель уже имеет достаточно полное понимание о строении графов, а также знает некоторые их свойства.

Третий раздел целиком посвящён базовым разновидностям неориентированных графов. В главах довольно основательно рассмотрены понятия полного графа, дерева, эйлерова графа и двудольного графа. Для каждого вида графов рассмотрено несколько основных свойств, признаков и теорем. Эти разновидности графов уже весьма и весьма часто используются в задачах школьной программы, а также и некоторых задачах олимпиадного уровня. Помимо прочего при помощи данных графов могут решаться и некоторые примеры классических комбинаторных задач. Знакомство читателей с данными графами является одной из основных задач моего пособия.

В следующем разделе пособия читатель знакомится с разновидностями ориентированных графов. Сначала ученик узнаёт основные свойства ориентированных графов в целом из первой главы раздела, затем знакомится с эйлеровым графом в ориентированных графах и гамильтоновым графом в ориентированных и неориентированных графах, а в последней главе раздела узнаёт о существовании турниров как аналогов полных графов в ориентированных графах. Ориентированные графы несколько отличаются от неориентированных, однако их использование не менее востребовано. Так, например, в заданиях ОГЭ по информатике есть задание на ориентированные графы и подсчёт числа путей из одной вершины в другую. После первой главы раздела читатель может увидеть на примере решение задачи такого типа.

Последний раздел методического пособия посвящён планарным графам. Введено определение планарного графа и несколько теорем, посвящённых ему. Как и всё, планарные графы рассмотрены ознакомительно. Тем не менее, сформулированы их базовые свойства, часть из которых предложены читателю для самостоятельного доказательства.

Структурно вся теория разделена на две большие части в соответствии с возрастом читателя. Так как темы усложняются, то на 6-7 класс ориентированными считаются первые три раздела, а четвёртый и пятый разделы рекомендованы для изучения школьниками 8-9 класса. Комплексное изучение теории из обеих частей позволяет сформировать у читателя достаточно ясное представление о предмете изучения теории графов.

Немалое место в составленном мной учебно-методическом пособии занимает практика, то есть практические задания, если быть точнее. Невозможно познакомить школьника с какой бы то ни было темой в каком бы то ни было предмете, не давая ему практики. Какие-то задания призваны помочь усвоить теорию, какие-то расширяют уже полученные теоретические сведения, а какие-то предлагают самому целиком построить логическое рассуждение, которое потом приводит к верному ответу, если повезёт.

Любое методическое пособие по математике содержит большое количество задач, можно даже сказать, что задачи – основная часть каждого учебно-методического пособия по математике. Теория направлена на то, чтобы познакомить читателя с основными понятиями, базовыми суждениями или распространёнными методами решения задач, но задачи позволяют глубже понять её, проработать способы решения и самостоятельно научиться развивать мысль. Благодаря задачной практике школьник развивает полученные знания, учится применять их, на что в конечном итоге и направлено обучение школьников какой бы то ни было теме…

Итак, мы поняли, насколько незаменим задачный практикум в подобных учебно-методических пособиях. Заметим также, что лучше иметь большую вариативность задач по сложности, формату выполнения и ключевой идее, чтобы тщательно отработать каждую тему. В моём учебно-методическом пособии задачи и упражнения приведены сразу после практически каждой главы. Чаще всего они следуют в порядке по усложнению, однако для удобства читателя существуют условные обозначения (см. далее). Для большинства из представленных тем существуют классические, типовые и распространённые задачи. Разумеется, для создания подборок задач к каждой главе я вновь прибегла к помощи специальной литературы. Вновь незаменимыми оказались «Графы» В. М. Гуровица и В. В. Ховриной, однако помимо них звание героев дня также заслужили книга С. А. Генкина, И. В. Итенберга и Д. В. Фомина «Ленинградские математические кружки», а также книга Н. Н. Горбачёва «Сборник олимпиадных задач по математике». Изучив материалы, представленные в этих книгах, я смогла подобрать подходящие для школьного уровня изучения задачи и прикрепить их к теоретическому минимуму по соответствующим темам. Однако на данном этапе я столкнулась с рядом проблем…

Во-первых, задачи из сборников безусловно обладают большой вариативностью в соответствии с идеей решения. Но большинство из задач сборников чересчур сложны для введения в школьную программу на ознакомительном уровне изучения. Может случиться так, что выбранные из сборников по темам и сложности задачи окажутся однотипными между собой. При таком раскладе может потеряться половина необходимости в них, задачи могут даже оказаться скучными для школьника.

С другой стороны, даже достаточно простые задачи с математических кружков и олимпиад не могут служить задачами по отработке теории для учеников общеобразовательной школы, не могут являться наглядной иллюстрацией к только что прочитанной теории и проверять, насколько ученик её усвоил. Итак, в используемых сборниках с классическими задачами олимпиад и кружков нет (или есть, но недостаточно) простых заданий на отработку теории. Общеобразовательная программа должна быть направлена на всех детей и подразумевать постепенное освоение ими материала, что не соответствует сжатым объяснениям на кружке, которые дают тебе только лёгкий толчок к решению задач. Нет, школьные задания должны иметь больший разброс сложности и наращивать её постепенно. К сожалению, как раз простые задания в сборниках пропускаются.

Последней отметим недостаточную вариативность в формате заданий. Упражнения и задачи в общеобразовательной программе часто бывают разных типов, в них стараются сформулировать любой возможный вопрос, а также развить у ученика и меж предметные навыки в том числе. Так, в задачах сборников почти никогда не встречаются тестовые задания и встречаются редко задания, где граф просят изобразить, привести пример или же изменить до определённого состояния. Эти задания кажутся простыми, однако разнообразие всегда добавляет интереса к процессу обучения, что тоже победа. Также можно заметить, что подобные задания можно усложнять дополнительными вопросами. Например, после выбора ответа в тесте можно ответить что-то про этот вариант ответа, охарактеризовать его или проанализировать. Подобные задания совместят наглядное применение теории с логическим рассуждением, которое однозначно пригодится в последующих задачах.

Таким образом, я сделала вывод о том, что было бы неплохо разнообразить подходящие задачи из сборников, где часто требуется доказательство или подсчёт и поиск ответа, тестовыми упражнениями и «творческими» заданиями. Графы – это, в первую очередь, про наглядность. Поэтому я снабдила своё пособие большим количеством картинок, среди которых необходимо найти нужный граф, или заданиями, которые формулируются как «Нарисуйте какой-нибудь граф такой, что…». Подобные задания справляются сразу с недостатком простых заданий на отработку теории и недостаточной вариативностью формата заданий. При этом мне показалось интересным разнообразить задачи и по идее решения, так что я придумала и несколько нестандартных задач посложнее (хоть их и значительно меньше, чем столь необходимых простых заданий). По паре «нестандартных» и простых задач моего сочинения вы можете найти в приложении.

Создание учебно-методического пособия не ограничивается написанием теоретической и практической части книги. Разумеется, необходимо подумать и о написании введения, указаний по работе с книгой, ответов и решений к задачам. Всё это также нашло отражение в моей работе.

Во введении мной было расписано, что данное пособие имеет целью познакомить учащихся 6-9 класса с основными положениями теории графов и помочь им научиться применять полученные знания. Здесь коротко описывается структура учебно-методического пособия, рассказывается о приводимых в книге задачах и их видах (см. подробнее далее). Немаловажно и то, что здесь указано, что пособие рассчитано на постепенное обучение. Это значит, что школьник, который по какой-либо причине начинает проходить материал учебно-методического пособия не с начала, обязан ознакомиться хотя бы с теоретическим минимумом по каждой из пропущенных тем.

Следующими после введения идут условные обозначения и советы по работе с пособием. Здесь часть, посвящённая советам, кажется мне достаточно классической. Внимания заслуживает, скорее, система условных обозначений. В теоретической части ими выделены основные теоремы и понятия, обособлена дополнительная информация. Условные обозначения также помогают читателю ориентироваться среди большого разнообразия задач. Так, мной были введены отдельные обозначения для базовых задач повышенной сложности, редких задач высокой сложности и базовых задач на доказательство второстепенных теорем или вспомогательных утверждений. Вся система условных обозначений призвана облегчить учащимся работу с пособием.

Далее по структуре как раз имеет место основная часть методического пособия: главы теории с задачами и иллюстрациями к ним.

В конце пособия содержатся ответы к абсолютному большинству задач, где требуется ответ, а в разделе указаний к решению приводятся решения или подсказки к самым сложным задачам, на мой взгляд, к задачам где могут потребоваться дополнительные знания или необычный подход.

В пособии большое внимание уделено иллюстрациям, поскольку одна из базовых мыслей, которые должны усвоить в самом начале школьники – «рисунок помогает решению». Иллюстрации тщательно проработаны в графической программе AutoCAD, они встречаются в качестве примера к теории или необходимы для решения и формулировки заданий. Так как графы могут являться наглядным способом представления информации, то без рисунков не обойтись ни при составлении глав учебно-методического пособия, ни при решении встретившихся в этом пособии задач.

В конце пособия содержится список литературы, а в самом начале оформлено содержание.

Я постаралась создать своё учебно-методическое пособие по всем правилам и оформить его с заботой о читателях. При работе над теоретической частью пособия я постаралась раскрыть нужным образом все необходимые темы, выбор и создание задач и упражнений призваны представить читателю разнообразные задачи, сложность в которых нарастает постепенно. Всё это оформлено в книгу, которая имеет целью сделать интересной и доступной для школьников теорию графов, по крайней мере – её основные положения.

При выполнении работы мной были изучены основные положения теории графов, после чего я использовала полученные знания при написании теоретической части своего учебно-методического пособия. Были созданы подборки задач к каждой главе теории. Во многих случаях подборки задач также дополнены упражнениями, которые я создала сама. Учебно-методическое пособие наполнено иллюстрациями, которые наглядно демонстрируют понятия, рассмотренные в теоретической части, или помогают при решении практических задач. К учебно-методическому пособию разработано введение, система условных обозначений, советы по работе с книгой, ответы и решения, список литературы. На заключительном этапе работы все перечисленные выше составляющие были собраны в одну книгу, которая и стала продуктом моего проекта. В будущем возможен выпуск дополненного издания, которое будет содержать больше теоретических тем для углублённого изучения и нестандартных задач к ним.

Итак, я считаю, что все поставленные задачи мной выполнены. Цель работы достигнута. В ходе работы над проектом я изучила основные положения теории графов и создала учебно-методическое пособие для школьников 6-9 класса под названием «Теория графов в рамках программы ФГОС».

1. А.А.Заславский, Б.Р.Френкин, А.В.Шалопалов. Задачи о турнирах. Издательство МЦНМО Москва, 2013.

2. Н.В.Горбачев. Сборник олимпиадных задач по математике. Издательство МЦНМО Москва, 2013.

3. А.Я.Канель-Белов, А.К.Ковальджи. Как решают нестандартные задачи. Издательство МЦНМО Москва, 2020

4. С.А.Генкин, И.В.Итенберг, Д.В.Фомин. Ленинградские математические кружки. Издательство МЦНМО Москва, 2021

5. В.М.Гуровиц, В.В.Ховрина. Графы. Издательство МЦНМО Москва, 2009.

6. https://foxford.ru/wiki/matematika/orientirovannye-grafy

7. https://stugum.files.wordpress.com/2014/03/harary-graph-theory.pdf

8. http://www.apmath.spbu.ru/grafomann/book-part1-par9.html

9. http://www.mi-ras.ru/~podolskii/files/chapters3-5.pdf

10. https://www.problems.ru/view_by_subject_new.php?parent=249&start=5

11. https://inf-oge.sdamgia.ru/test?theme=22

12. https://reshator.com/sprav/algebra/7-klass/reshenie-prostyh-kombinatornyh-zadach-s-pomoshchyu-grafov/

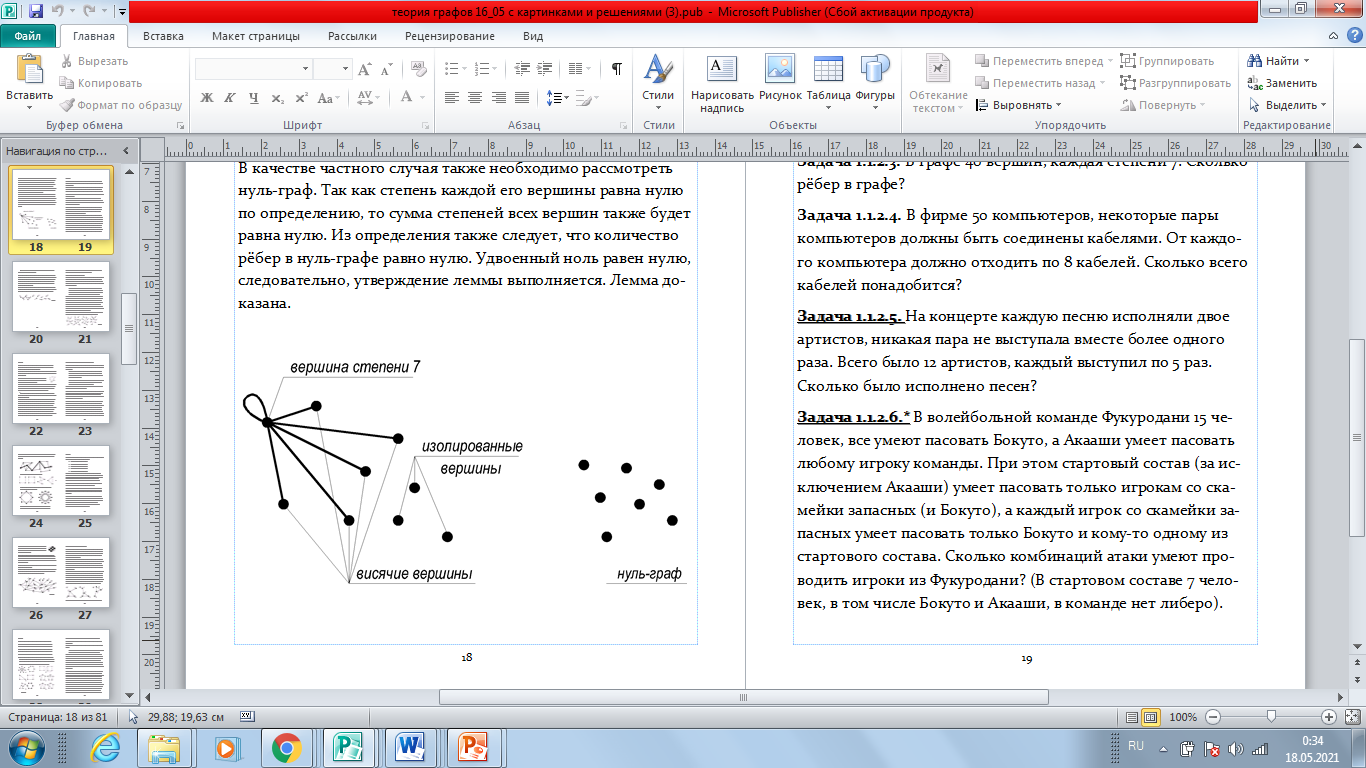
Рисунок 1. «Нестандартная» задача, придуманная мной (здесь и далее взяты картинки из цифрового варианта методического пособия)

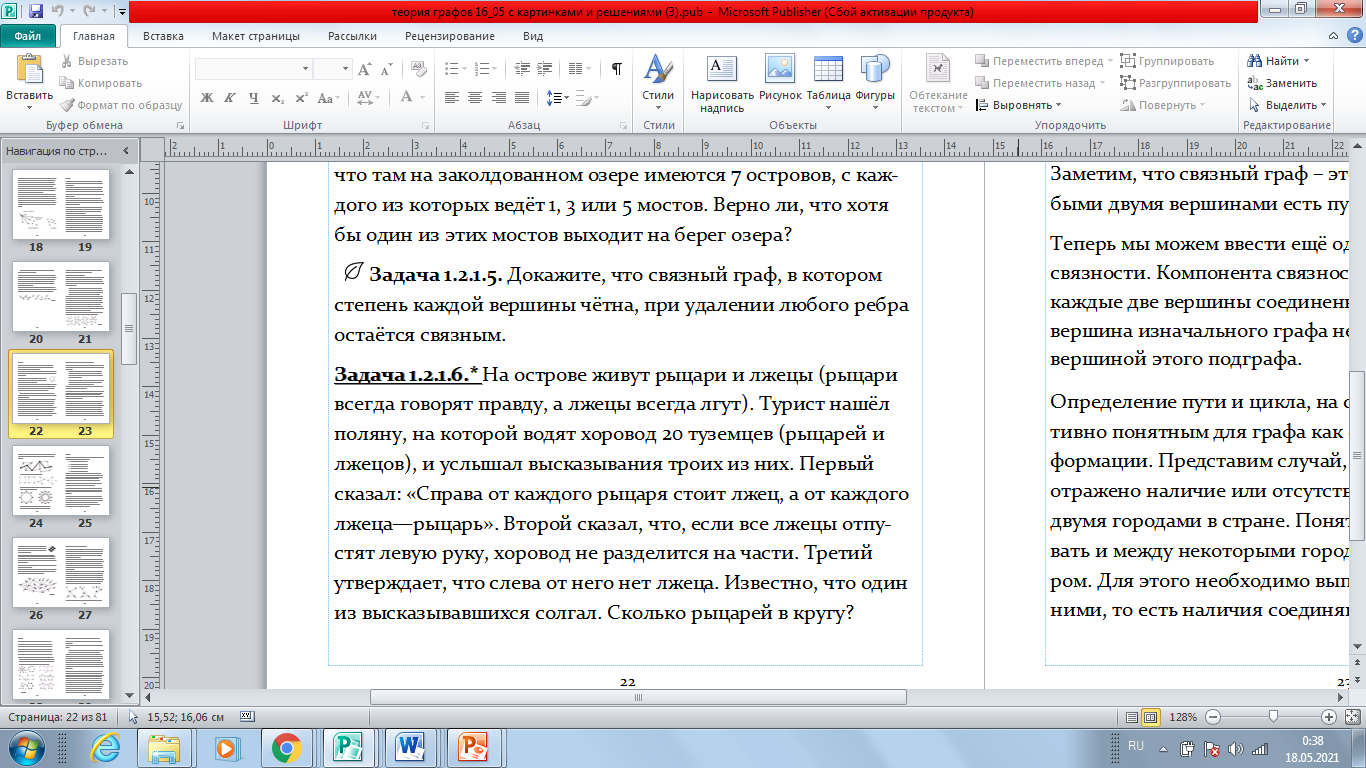
Рисунок 2. «Нестандартная» задача, придуманная мной

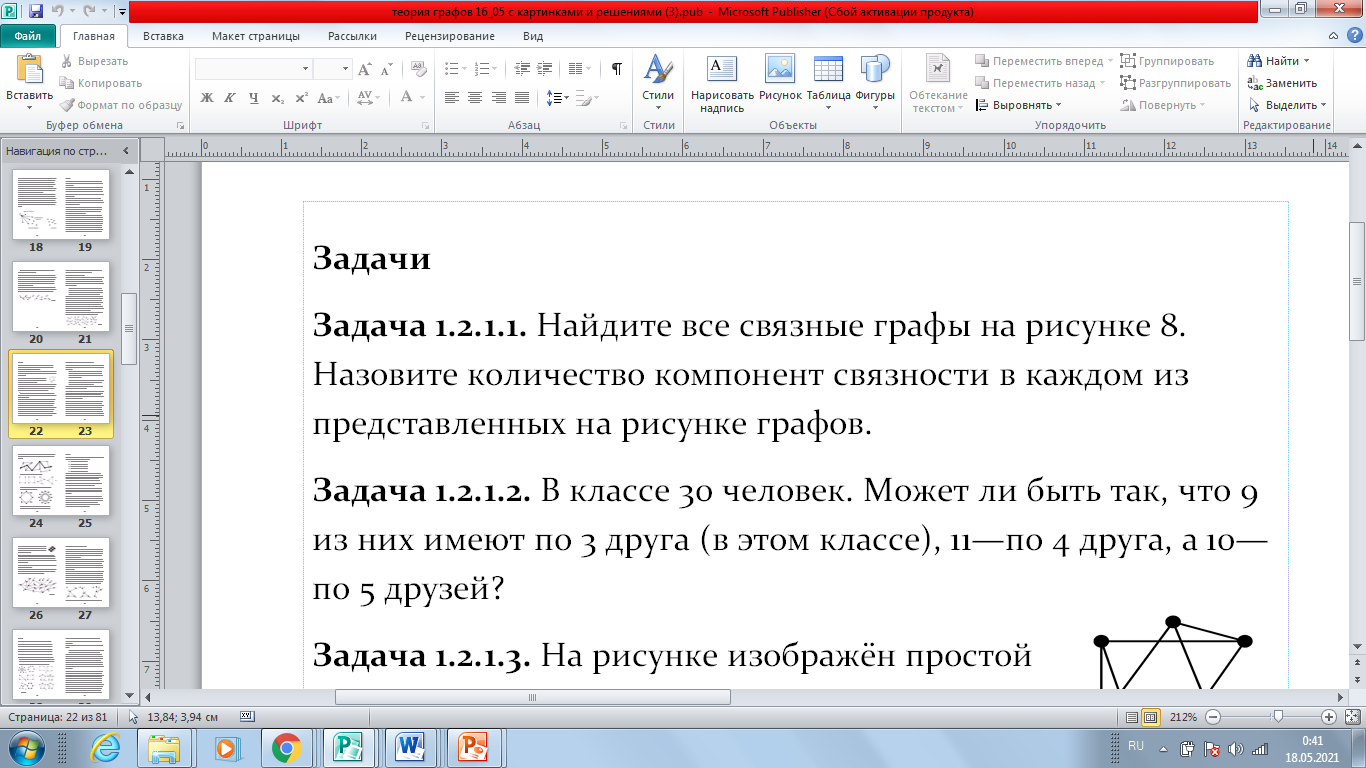
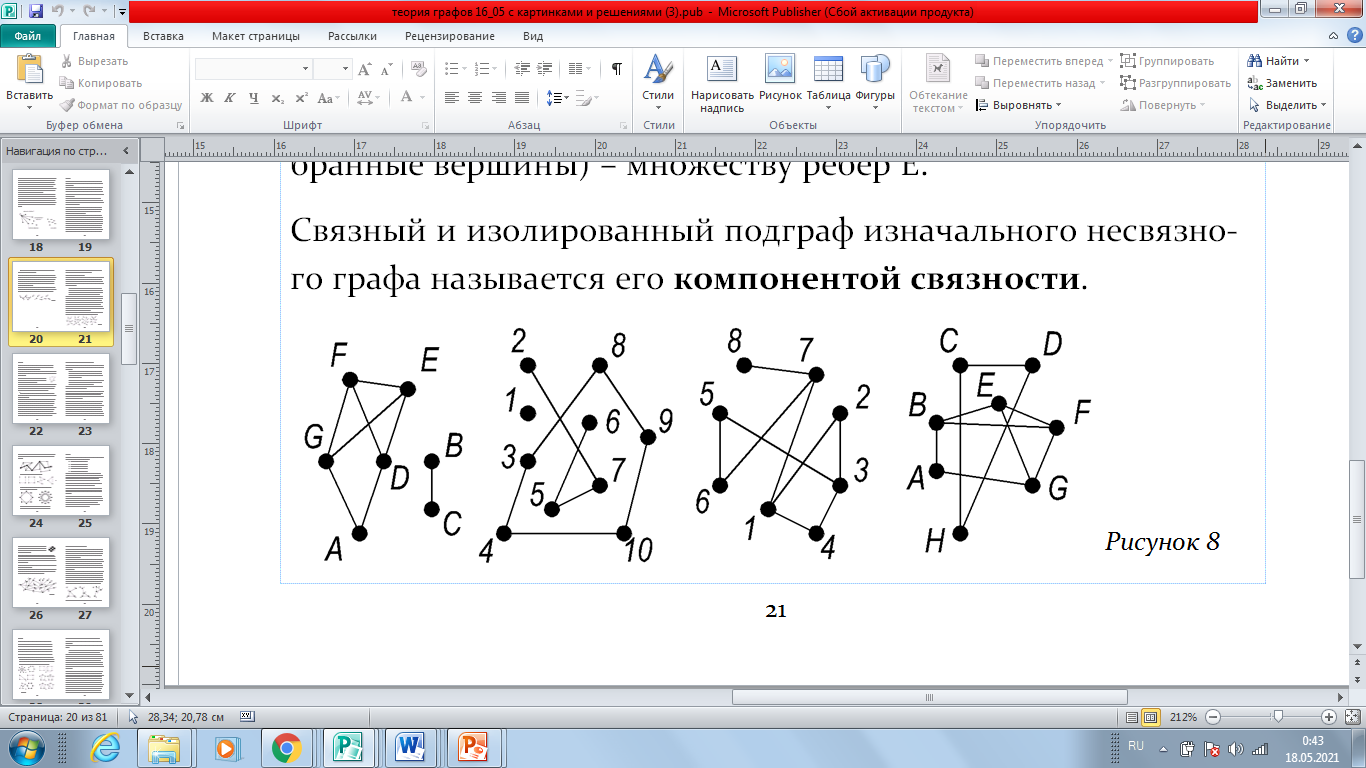
Рисунок 3. Простая задача с элементом тестового ответа, придуманная мной