Комитет образования и науки Курской области
Областное бюджетное профессиональное образовательное учреждение
«Рыльский аграрный техникум»
Индивидуальный проект
по предмету: «Информатика»
на тему: «Использование табличного процессора MS Excel в профессиональной деятельности»
Выполнила студентка
Толкачева Ирина Сергеевна,
очная форма, профессия
«Повар, кондитер»
Руководитель:
преподаватель Матюхина Ю.В.
Рыльск 2019г.
ОГЛАВЛЕНИЕ
Введение 3
1. Технология обработки числовых данных
1.1 Общая характеристика табличного процессора MS Excel 4
1.2. Вычисления в электронной таблице MS Excel 5
1.3. Надстройки MS Excel 7
2. Решение профессиональных задач средствами MS Excel
2.1. Калькуляция себестоимости готовой продукции 11
2.2. Решение задач оптимально планирования 13
Заключение 18
Библиографический список 19
Приложения 20
ВВЕДЕНИЕ
Современный период развития общества характеризуется сильным влиянием на него компьютерных технологий, проникающих во все сферы человеческой деятельности. Поэтому обязательным компонентом подготовки любого специалиста является умение использовать компьютер для решения профессиональных задач. Будущие специалисты должны обладать системой знаний и умений, позволяющих грамотно использовать компьютерные технологии в своей профессиональной деятельности.
Выпускникам по профессии «Повар, кондитер» необходимо уметь составлять калькуляционные карты, технологические карты, производить расчет количества продуктов для приготовления блюд, осуществлять оптимальное планирование выпуска продукции и решать другие вычислительные задачи.
Цель проекта – рассмотреть возможности табличных процессоров для решения профессиональных задач повара, кондитера.
Задачи:
• Изучить теоретический материал о вычислительных возможностях табличных процессоров;
• Разработать ассортимент блюд, рассчитать и составить технологические карты;
• Создать калькуляционные карты с автоматическим расчетом себестоимости блюд и цены продажи блюда;
• Познакомиться с использование электронной таблицы для решения задач оптимального планирования.
Объект исследования – табличный процессор. Предмет исследования – программа MS Excel.
-
ТЕХНОЛОГИЯ ОБРАБОТКИ ЧИСЛОВЫХ ДАННЫХ
1.1 Общая характеристика табличного процессора MS Excel
Табличный процессор Microsoft Excel представляет собой электронную таблицу, которая предназначена не только для составления таблиц различной степени сложности, но и для ведения различного рода отчетности (бухгалтерской, складской и др.). Помимо этого Microsoft Excel позволяет легко производить различные расчеты, строить графики и диаграммы, вести базы данных.
Microsoft Excel предназначен для работы с электронными таблицами (Sheets), позволяющими собирать, анализировать и представлять в удобном виде количественную и текстовую информацию.
Электронная таблица – самая распространенная и мощная технология для профессиональной работы с данными. В ячейках таблицы могут быть записаны данные различных типов: текст, даты, числа, формулы и др. Главное достоинство электронной таблицы – возможность мгновенного автоматического пересчета всех данных, связанных формульными зависимостями, при изменении значения любого компонента таблицы.
Основные возможности электронных таблиц:
1. Проведение однотипных сложных расчётов над большими наборами данных.
2. Автоматизация итоговых вычислений.
3. Решение задач путём подбора значений параметров.
4. Обработка (статистический анализ) результатов экспериментов.
5. Проведение поиска оптимальных значений параметров (решение оптимизационных задач).
6. Подготовка табличных документов.
7. Построение диаграмм по имеющимся данным.
8. Создание и анализ баз данных (списков).
Программа обработки электронных таблиц MS Excel обеспечивает пользователя богатым набором возможностей создания и изменения таблиц, которые могут содержать числа, текст, даты, денежные единицы, графику, а также математические и иные формулы для выполнения вычислений. Ввод данных в таблицы, их форматирование и выполнение различного рода вычислений в значительной степени автоматизированы. Предусмотрены средства представления числовых данных в виде диаграмм, создания, сортировки и фильтрации списков, статистического анализа данных и решения оптимизационных задач.
Кроме специфических инструментов, характерных для работы с электронными таблицами, MS Excel обладает стандартным для приложений Windows набором файловых операций, имеет доступ к буферу обмена и механизмам отмены и возврата.
Документы MS Excel записываются в файлы, имеющие расширение .xlsx. Кроме того, MS Excel может работать с электронными таблицами и диаграммами, созданными в других распространенных пакетах (например, Lotus 1-2-3), а также преобразовывать создаваемые им файлы для использования их другими программами.
-
Вычисления в электронной таблице MS Excel
Вычисления в таблицах программы Excel осуществляются при помощи формул. Формулой в Excel называется последовательность символов, начинающаяся со знака равенства “=“. В эту последовательность символов могут входить постоянные значения, ссылки на ячейки, имена, функции или операторы. Результатом работы формулы является новое значение, которое выводится как результат вычисления формулы по уже имеющимся данным.
Операторами обозначаются операции, которые следует выполнить над операндами формулы. В Microsoft Excel включено четыре вида операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Арифметические операторы служат для выполнения арифметических операций, таких как сложение, вычитание, умножение. Операции выполняются над числами. Операторы сравнения используются для сравнения двух значений. Результатом сравнения является логическое значение: либо ИСТИНА, либо ЛОЖЬ. Текстовый оператор конкатенации (&) используется для объединения нескольких текстовых строк в одну строку. Операторы ссылки применяют для описания ссылок на диапазоны ячеек.
Формулы вычисляют значения в определенном порядке. Формула вычисляется слева направо, в соответствии с определенным порядком для каждого оператора в формуле. Для того чтобы изменить порядок выполнения, заключите часть формулы, которая должна выполняться первой, в скобки.
Для выполнения табличных вычислений нужны формулы. Поскольку некоторые формулы и их комбинации встречаются очень часто, то программа Excel предлагает более 200 заранее запрограммированных формул, которые называются функциями.
Все функции разделены по категориям, чтобы в них было проще ориентироваться. Встроенный Конструктор функций помогает на всех этапах работы правильно применять функции. Он позволяет построить и вычислить большинство функций за два шага.
В программе имеется упорядоченный по алфавиту полный список всех функций, в котором можно легко найти функцию, если известно ее имя; в противном случае следует производить поиск по категориям. Многие функции различаются очень незначительно, поэтому при поиске по категориям полезно воспользоваться краткими описаниями функций, которые предлагает Конструктор функций. Функция оперирует некоторыми данными, которые называются ее аргументами. Аргумент функции может занимать одну ячейку или размещаться в целой группе ячеек. Конструктор функций оказывает помощь в задании любых типов аргументов.
Функции в Excel используются для выполнения стандартных вычислений в рабочих книгах. Значения, которые используются для вычисления функций, называются аргументами. Значения, возвращаемые функциями в качестве ответа, называются результатами. Помимо встроенных функций вы можете использовать в вычислениях пользовательские функции, которые создаются при помощи средств Excel. Чтобы использовать функцию, нужно ввести ее как часть формулы в ячейку рабочего листа.
Последовательность, в которой должны располагаться используемые в формуле символы, называется синтаксисом функции. Все функции используют одинаковые основные правила синтаксиса. Аргументы функции записываются в круглых скобках сразу за названием функции и отделяются друг от друга символом точка с запятой “;”. В качестве аргументов можно использовать числа, текст, логические значения, массивы, значения ошибок или ссылки. Аргументы могут быть как константами, так и формулами.
В свою очередь формулы могут содержать другие функции. Функции, являющиеся аргументом другой функции, называются вложенными. В формулах Excel можно использовать до семи уровней вложенности функций. Задаваемые входные параметры должны иметь допустимые для данного аргумента значения. Некоторые функции могут иметь необязательные аргументы, которые могут отсутствовать при вычислении значения функции.
-
Надстройки MS Excel
Надстройки — это программы, входящие в состав Microsoft Excel и расширяющие его возможности.
Рассмотрим надстройки Подбор параметра и Поиск решения.
Команда Подбор параметра меню Сервис позволяет определить неизвестное значение (параметр), которое будет давать желаемый результат. Технология использования команды следующая:
-
решить нужную задачу с каким-либо начальным значением параметра;
-
выбрать команду Подбор параметра меню Сервис;
-
в окне диалога Подбор параметра в поле Установить в ячейке задать абсолютную ссылку на ячейку, содержащую расчетную формулу, а в поле Значение — то значение, которое следует получить в качестве результата формулы;
-
в поле Изменяя значение ячейки ввести ссылку на ячейку с параметром;
-
нажать кнопку ОК или клавишу Enter, на экране появится окно диалога Результат подбора параметра;
-
для сохранения найденного значения нажать кнопку ОК. Для восстановления значения, которое было в ячейке с параметром до использования команды Подбор параметра нажать кнопку Отмена.
При подборе параметра Excel использует итерационный процесс. Он проверяет для изменяемой ячейки одно значение за другим, пока не получит нужное решение.
Если задача подбора параметра занимает много времени, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы просмотреть результаты последовательных итераций.
По умолчанию команда Подбор параметра прекращает вычисления, когда выполняется 100 итераций, или при получении результата, который находится в пределах 0,001 от заданного целевого значения. Если нужна большая точность, можно изменить используемые по умолчанию параметры на вкладке Вычисления команды Параметры меню Сервис.
Команда Подбор параметра находит только одно решение, даже если задача имеет несколько решений.
Поиск решений может применяться для решения задач, которые включают много изменяемых ячеек, и помогает найти комбинацию переменных, которые максимизируют или минимизируют значение в целевой ячейке. Он также позволяет задать одно или несколько ограничений условий, которые должны выполняться при поиске решений. Для запуска этого инструмента следует выполнить команду Поиск решения меню Сервис.
В диалоговом окне Поиск решения в поле Установить целевую ячейку задается цель, которую должен достичь поиск решения. Целевая ячейка может быть задана ссылкой или именем. Поиск решения может находить конкретное значение целевой функции. В этом случае, задав только изменяемую ячейку без указания ограничений, можно использовать Поиск решения вместо команды Подбор параметра.
Цель поиска решений может не задаваться. Тогда поле Установить целевую ячейку следует оставить пустым, нажать кнопку Параметры и установить флажок Показывать результаты итераций. Поиск решения будет перебирать комбинации изменяемых ячеек, которые удовлетворяют заданным ограничениям. Пользователь может выбрать нужное решение, но оно необязательно будет оптимальным.
В поле Изменяя ячейки следует задать ячейки с переменными. Можно указать ссылки на ячейки или их имена. Если ячейки находятся в несмежных диапазонах, их следует разделять точкой с запятой. Вместо ввода ячеек можно нажать кнопку Предположить, и поиск решения сам предложит изменяемые ячейки, исходя из заданной целевой функции. Поле Изменяя ячейки нельзя оставить пустым, и указанные в нем ячейки обязательно должны влиять на значение целевой ячейки.
Последний шаг определения поиска решений — задание ограничений. Он не является обязательным. Чтобы задать ограничения, следует в окне Поиск решения нажать кнопку Добавить и заполнить окно диалога Добавление ограничений. Ограничение состоит из трех компонентов: ссылки на ячейку, оператора сравнения и значения ограничения. В левой части от оператора сравнения кроме ссылки на ячейку может также задаваться ссылка на диапазон. В правой части может задаваться диапазон (той же размерности, что и в левой части), ссылка на ячейку или константное значение.
После заполнения диалогового окна Поиск решения следует нажать кнопку Выполнить. При нахождении оптимального решения на экран выводится диалоговое окно Результаты поиска решения. Значения, отображаемые в рабочем листе, представляют собой оптимальное решение задачи. Можно либо оставить эти значения на листе, если установить переключатель Сохранить найденное решение и нажать кнопку ОК, либо восстановить исходные значения, если нажать кнопку Отмена или установить переключатель Восстановить исходные значения и нажать кнопку ОК. Можно также сохранить найденные значения в качестве сценария.
Поиск решений может решить не каждую предложенную задачу. Если оптимальное решение не найдено, в окне диалога Результаты поиска решений выводится сообщение о неуспешном завершении.
2. Решение профессиональных задач средствами MS Excel
2.1. Калькуляция себестоимости готовой продукции
Задача калькуляции себестоимости готовой продукции является одной из важнейших в сфере финансового и управленческого учета предприятия. Достоверная информация о фактической себестоимости выпуска, нормативных и фактических затратах товарно-материальных ресурсов дает возможность менеджменту компании принимать адекватные управленческие решения в сфере ценообразования готовой продукции тем самым, обеспечивая прибыльную деятельность предприятия.
Помимо выполнения главной задачи ценообразования калькуляция себестоимости также обеспечивает контроль движения основных позиций товарно-материальных запасов предприятия.
Вопрос калькуляции себестоимости готовой продукции является особо актуальным для предприятий общественного питания: кафе, ресторанов, баров и т.д.
Расчет отпускных цен на готовые блюда предприятий общепита производят на основе специальных калькуляционных карточек формы ОП-1 для каждого вида продукции. Калькуляцию составляют в расчете на одно или сто блюд. Чтобы наиболее точно определить цены реализации, рекомендуется производить калькуляцию на сто блюд.
Расчет продажных цен производится на каждое блюдо. Перед составлением калькуляции необходимо иметь ассортиментный перечень блюд, состав и нормы ингредиентов по списку рецептур или технологическим картам, закупочные цены на продукты.
Калькуляция производится в следующем порядке:
-
Определяется перечень блюд, на которые составляется калькуляция.
-
На основании сборника рецептур и технологических карт устанавливаются нормы вложений всех ингредиентов в готовое блюдо.
-
Определяются закупочные цены на сырье и ингредиенты.
-
Производится расчет стоимости сырьевого набора блюд путем умножения количества сырья на продажную цену и суммированием по всем позициям номенклатуры ингредиентов.
-
Сырьевая стоимость одного блюда получается путем деления общей суммы на 100.
-
Цена продажи готового блюда исчисляется путем увеличения сырьевой стоимости на величину торговой наценки (в %), устанавливаемой приказом руководителя предприятия общепита.
Наиболее оптимальным вариантом организации системы калькуляции является внедрение автоматизированной системы финансового учета, связывающей воедино все материально-финансовые потоки заведения.
Например, к таким системам можно отнести MS Excel. На первом этапе определяем ассортимент блюд из рубленного мяса. Затем составляем технологические карты для каждого блюда в соответствии с нормативами по Сборнику рецептур, выполняем расчет сырья на 100 порций по формулам. После чего оформляем калькуляционные карты блюда, выполнив необходимые расчеты себестоимости и продажной цены.
Разработанная в проекте система таблиц калькуляции блюд может быть использована:
1. при изучении теоретического материала и подготовке к практическим и лабораторным работам по профессиональным модулям
2. при подготовке выпускной квалификационной работы;
3. на предприятиях общественного питания.
2.2. Решение задач оптимально планирования
Постановка задачи планирования выглядит следующим образом:
• Имеются некоторые плановые показатели.
• Имеются некоторые ресурсы, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены.
• Имеется определенная стратегическая цель, зависящая от плановых показателей, на которую следует ориентировать планирование.
Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.
Рассмотрим пример: Кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 изделий. Рабочий день в кондитерском цехе длится 8 часов. Если выпускать только пирожные, за день можно произвести не более 250 штук, пирожков же можно произвести 1000, если при этом не выпускать пирожных. Стоимость пирожного вдвое выше, чем пирожка. Требуется составить дневной план производства, обеспечивающий кондитерскому цеху наибольшую выручку.
Чтобы составить дневной план производства, составим математическую модель задачи.
Плановыми показателями являются:
• х — дневной план выпуска пирожков;
• у — дневной план выпуска пирожных.
Ресурсы производства это:
• длительность рабочего дня — 8 часов;
• вместимость складского помещения — 700 мест.
Предполагается для простоты, что другие ресурсы (сырье, электроэнергия и пр.) не ограничены. Формализацию цели (достижение максимальной выручки цеха) мы обсудим позже.
Получим соотношения, следующие из условий ограниченности времени работы цеха и вместимости склада, т. е. суммарного числа изделий.
Из постановки задачи следует, что на изготовление одного пирожного затрачивается в 4 раза больше времени, чем на выпечку одного пирожка. Если обозначить время изготовления пирожка как t мин, то время изготовления пирожного будет равно 41 мин. Значит, суммарное время на изготовление х пирожков и у пирожных равно
tx + 4ty = (х + 4y)t.
Но это время не может быть больше длительности рабочего дня. Отсюда следует неравенство:
(х + 4y)t ≤ 8 • 60,
или
(х + 4y)t ≤ 480.
Легко посчитать t — время изготовления одного пирожка. Поскольку за рабочий день их может быть изготовлено 1000 штук, на один пирожок тратится 480/1000 = 0,48 мин. Подставляя это значение в неравенство, получим:
(х + 4у) • 0,48 ≤ 480.
Отсюда
х + 4у ≤ 1000.
Ограничение на общее число изделий дает совершенно очевидное неравенство:
х + у ≤ 700.
К двум полученным неравенствам следует добавить условия положительности значений величин х и у (не может быть отрицательного числа пирожков и пирожных). В итоге получим систему неравенств:

А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка — r рублей. По условию задачи, цена пирожного в два раза больше, т. е. 2r рублей. Отсюда стоимость всей произведенной за день продукции равна
rх + 2rу = r(х + 2у).
Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:
F(x, у) = r(х + 2у).
Она называется целевой функцией.
Поскольку значение r — константа, максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять
f(x, у) = х + 2у. (2)
Следовательно, получение оптимального плана свелось к следующей математической задаче:
Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств (1) и придающих максимальное значение целевой функции (2).
Итак, математическая модель задачи оптимального планирования для кондитерского цеха построена.
Реализуем поиск оптимального решения для задачи планирования работы кондитерского цеха в MS Excel.
Подготовим электронную таблицу:
|
| A | B | C | D |
| 1 | Оптимальное планирование |
| 2 | Плановые показатели | X (пирожки) | Y (пирожные) |
|
| 3 |
|
|
|
|
| 4 | Ограничения |
|
|
|
| 5 |
| левая часть | знак | правая часть |
| 6 | время производства | =B3+4*C3 | | 1000 |
| 7 | общее количество | = B3+C3 | | 700 |
| 8 | положительность Х | =B3 | = | 0 |
| 9 | положительность Y | =C3 | = | 0 |
| 10 | Целевая функция | = B3+2*C3 |
|
|
Воспользуемся программой оптимизации «Поиск решения».
Для этого выполним команду Сервис — Поиск решения (если такой команды нет, то ее можно добавить Сервис — Настройки — установить флажок Поиск решения)
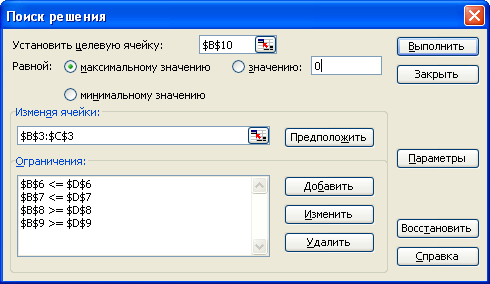
В диалоговом окне Поиск решения укажем:
-
адрес ячейки с целевой функцией, установить переключатель максимальное значение
-
в поле «изменяя ячейки» адреса ячеек, содержащих плановые показатели
-
в поле «ограничения», пользуясь кнопкой Добавить указать все имеющиеся ограничения
-
т.к. задача является линейной, то щелкнуть по кнопке Параметры и в открывшимся диалоговом окне установить флажок Линейная модель.
-
для получения решения щелкнуть по кнопке Выполнить.
В результате применения инструмента Поиск решения получен следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных.
ЗАКЛЮЧЕНИЕ
Табличный процессор – это прикладная программа, предназначенная для организации табличных вычислений на компьютере.
Вычислительная таблица, которая создаётся с помощью табличного процессора, называется электронной таблицей.
Одним из самых популярных табличных процессоров сегодня является MS Excel, входящий в состав MicrosoftOffice.
В данной работе были изучены основные характеристики табличного процессора MS Excel, раскрыты его основные функции, вычислительные возможности, надстройки. А также во второй главе рассмотрели возможности табличных процессоров для решения профессиональных задач повара, кондитера.
Таким образом, для решения ряда профессиональных задач целесообразно использовать многочисленные возможности табличных процессоров. Знание табличного процессора облегчит наш труд по созданию и заполнению калькуляционных карт и тех документов, где необходимы расчеты для осуществления профессиональной деятельности.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
-
Информатика и ИКТ: учебник для нач. и сред. проф. образования/ М.С. Цветкова, Л.С. Великович. – 3-е изд., стер. – М.: Издательский центр «Академия», 2012. – 352 с.: ил.
-
Информатика. 11-й класс/ И.Г. Семакин, Е.К. Хеннер. – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2005. – 139 с.: ил.
-
Информатика и информационные технологии. Учебник для 10-11 классов/ Н.Д. Угринович. - М.: БИНОМ. Лаборатория знаний, 2003. – 512 с.: ил.
-
http://www.studfiles.ru/preview/5999270/





























