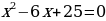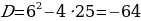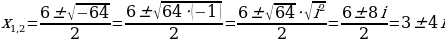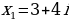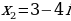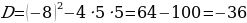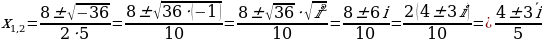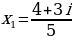| МИНИСТЕРСТВО ОБРАЗОВАНИЯ ЯРОСЛАВСКОЙ ОБЛАСТИ
ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ЯРОСЛАВСКОЙ ОБЛАСТИ
ЯРОСЛАВСКИЙ КОЛЛЕДЖ ИНДУСТРИИ ПИТАНИЯ |
|
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
тема
|
| «Комплексные числа» |
| учебный предмет | ОУПП.12 МАТЕМАТИКА |
|
| (код и название дисциплины по учебному плану) |
|
|
| специальность/ профессия | 19.02.03 Технология хлеба, кондитерских и макаронных изделий |
|
| (код. название специальности/профессии) |
|
| Работу выполнил | | студент гр. |
| |
| | (фамилия, инициалы студента) | |
| | Руководитель проекта | |
| | (фамилия, инициалы преподавателя) | |
| | « |
| .» |
| 2023 г. | |
| | По итогам защиты проекта | | оценка |
| | Председатель комиссии | |
|
|
| | (подпись) |
| (расшифровка) |
|
|
г. Ярославль, 2023 |
ПАСПОРТ ПРОЕКТА
| Тема проекта | Комплексные числа |
| Цель | Изучение истории возникновения и применения комплексных чисел. |
| Задачи | 1. Проанализировать литературу по данному вопросу. 2. Ознакомиться с историей чисел и комплексных чисел. 3. Исследовать действия над комплексными числами. 4. Оценить значение и роль комплексных чисел в математике. 5. Научиться решать квадратные уравнения с отрицательным дискриминантом. |
| Продукт
проектной деятельности | Буклет |
| Тип проекта | Исследовательский |
| Учебные предметы,
к которым проект имеет отношение | Математика |
| Разработчик проекта (ФИО полностью) |
|
| Руководитель проекта (ФИО полностью) |
|
| Учебный год, в котором разрабатывался проект | 2022 / 2023 учебный год |
СОДЕРЖАНИЕ
ВВЕДЕНИЕ………………………………………………………………………4
ГЛАВА I. КОМПЛЕКСНЫЕ ЧИСЛА……………………………………….6
-
История чисел……………………………………………………………….6
-
История открытия комплексных чисел……………………………………6
-
Понятие комплексного числа………………………………………………7
ГЛАВА II. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕННИЙ В ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ…………………………………………………..9
-
Действия над комплексными числами……………………………………9
-
Решение квадратных уравнений…………………………………………..9
ЗАКЛЮЧЕНИЕ………………………………………………………………12
СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ……………………13
ВВЕДЕНИЕ
В незапамятные времена, научившись считать, люди познали меру количества - числа. Число одно из основных понятий математики, зародилось в глубокой древности и постепенно расширялось, и обобщалось. В течении тысячелетий люди использовали пальцы рук и ног, но это было не очень удобно при обозначении большого количества. Возникла необходимость более удобного способа выражения количества. Таким способом является запись чисел при помощи специальных знаков - цифр. Каждый из нас в жизни сталкивается с числами. Курс школьной программы, да и дальнейшую жизнь, трудно представить без них. Давайте рассмотрим в проекте историю развития комплексных чисел, различные формы записи комплексных чисел, операции, выполнимые на множестве комплексных чисел, применение их в математике.
Цель моего проекта:
Изучение истории возникновения и применения комплексных чисел.
Задачи проекта:
1. Проанализировать литературу по данному вопросу.
2. Ознакомиться с историей чисел и комплексных чисел.
3. Исследовать действия над комплексными числами.
4. Оценить значение и роль комплексных чисел в математике.
5. Научиться решать квадратные уравнения с отрицательным дискриминантом.
Гипотеза:
Квадратные уравнения с отрицательным дискриминантом имеют решение.
Методы исследования:
1. Изучение и анализ литературных источников.
2. Сбор информации по теме.
3. Анализ проделанной работы.
ГЛАВА 1. КОМПЛЕКСНЫЕ ЧИСЛА
1.1. История чисел
В древние времена, когда человек хотел показать сколькими животными он владел, он клал в большой мешок столько камешков, сколько у него было животных. Чем больше животных, тем больше камешков. Отсюда и произошло слово «калькулятор», «калькулюс» по-латински означает «камень».
Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги. Поэтому, если в те времена кто-то хвалился, что у него «две руки и одна нога кур», это означало, что у него пятнадцать кур, а если это называлось «весь человек», то есть две руки и две ноги.
Жизнь текла свои чередом, всё менялось, людям нужны были какие-то ещё знаки, кроме пальцев. Числа становились всё больше, трудно было удерживать их в голове, следовало как-то их обозначить и записать. Так появились цифры, первыми были египтяне, потом греки и ремляне. Сейчас мы иногда пользуемся римскими цифрами. Однако самыми популярными и используемыми нами по сей день являются цифры, изобретённые в Индии ещё до начала V века. Почему же привычные цифры называются арабскими, ведь они был придуманы в Индии? А всё потому, что распространение они получили именно благодаря арабским странам, которые их начали активно использовать. Среди тех, кто помогал миру открыть хорошо знакомые нам арабские цифры, был француз Александр де Виллие, британский учитель Джон Галефакс и знаменитый математик Фибоначчи, которые часто путешествовали на Восток и изучали труды арабских ученых.
Само слово «цифра» арабского происхождения. Созвучное арабское слово «сифир» обозначает те значки, которые мы привыкли использовать 0, 1, 2 ... 9.
1.2. История открытия комплексных чисел
История комплексных чисел, как считается, начинается в XVI веке, когда итальянский математик Джелорамо Кардано при решении кубических уравнений получил весьма интересные значения с отрицательным подкоренным выражением.
Но только через 300 лет началось использование комплексных чисел в науке и технике. Старт применению комплексных чисел в электротехнике положил доклад знаменитого электротехника Штейнмеца на Международном конгрессе по электротехнике в г. Чикаго (1893 г.)
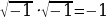
Комплексные числа применяются в электротехнике для расчёта электрических цепей переменного и постоянного тока. Причём как для упрощения расчётов, так и как единственный способ расчёта. Они позволяют заменить графические векторные решения на привычные нам алгебраические.
1.3. Понятие комплексного числа
В множестве действительных чисел действие извлечения корня четной степени из отрицательного числа невыполнимо.
Выражение 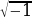 ,
, 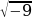 ,
, 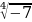 не имеют смысла и, поэтому, уравнения
не имеют смысла и, поэтому, уравнения
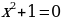 ,
, 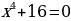 ,
, 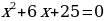
на этом множестве решений не имеют.
Для того, чтобы сделать возможным извлечение корня четной степени из отрицательного числа множество действительных чисел было расширено добавлением к нему множества мнимых чисел.
Определение 1.
Число, квадрат которого равен -1, называется мнимой единицей и обозначается буквой 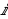
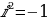
Комплексное число имеет вид z = a +bi, где a и b – действительные числа, i – так называемая мнимая единица. Число a называется действительной частью комплексного числа z, число b называется мнимой частью комплексного числа z.
a + bi – это единое число, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: 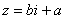 или переставить мнимую единицу:
или переставить мнимую единицу: 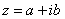 – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:
– от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: 
ГЛАВА 2. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕННИЙ В ПОЛЕ КОМПЛЕКСНЫХ ЧИСЕЛ
2.1. Действия над комплексными числами
Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания, умножения и деления.
Сложение и умножение комплексных чисел подчиняется тем же законам, что и сложение и умножение действительных чисел!
Пример: Пусть 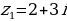
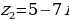
Найдем: 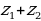 ;
; 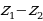 ;
; 

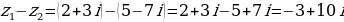

С делением немного сложнее. Для начала нужно ввести новое понятие, а именно сопряженное комплексное число данному комплексному числу.
Сопряженным числом z числу 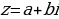 называется такое число, что
называется такое число, что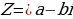 . То есть в сопряженном числе знак между действительной и мнимой частями всегда противоположен знаку того числа, с которым он сопряжен.
. То есть в сопряженном числе знак между действительной и мнимой частями всегда противоположен знаку того числа, с которым он сопряжен.
Пример: 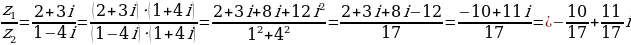
Возведение комплексных чисел в степень. Что делать, если комплексное число нужно возвести в какую-либо степень? Ясно, что в алгебраической форме проделать такое действия практически невозможно. Тогда можно воспользоваться можно использовать так называемою формула Муавра. Из операции умножения комплексных чисел следует, что
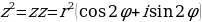
В общем случае получим:
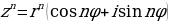
Где n – целое положительное число.
Пример: Дано комплексное число 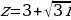 , найти
, найти 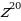
Сначала нужно представить данное число в тригонометрической форме
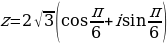
Тогда, по формуле Муавра:
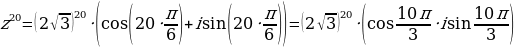
2.2 Решение квадратных уравнений
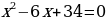
Дискриминант: 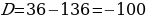
D
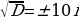
Получаются два корня:
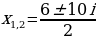
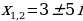 -сопряженные комплексные корни
-сопряженные комплексные корни
Таким образом, уравнение 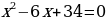 имеет два сопряженных комплексных корня:
имеет два сопряженных комплексных корня:
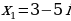 ,
, 
Ответ: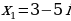 ,
, 
Рассмотрим еще один пример: 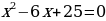
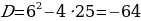
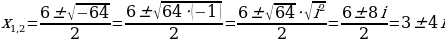
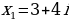
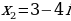
Ответ: 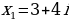
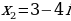
В принципе не сильно отличаются эти примеры от обычных. Только в конце дописывается мнимая единица.

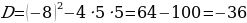
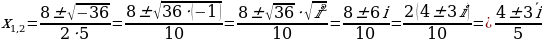
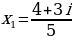
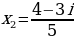
Ответ: 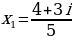
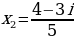
ЗАКЛЮЧЕНИЕ
В данной работе мне удалось решить все поставленные задачи, проанализировать литературные источники, которые раскрыли представление о понятии комплексного числа. Узнала много интересных фактов из истории происхождения цифр. Подобраны и решены примеры с использованием комплексных чисел, ходящие в курс математики. Работая над проектом, я убедилась, что квадратные уравнения с отрицательным дискриминантом имеют решение в поле комплексных чисел. Гипотеза о том, что квадратные уравнения с отрицательным дискриминантом умеют решение в поле комплексных чисел, подтвердилась.
Определений и свойств у комплексных чисел очень много, все не перечислишь. Я бы отметила такой аспект: комплексные числа можно понимать, как алгебраическое замыкание вещественных чисел. Если по-просту, то это такая (минимальная) система в которой все алгебраические уравнения разрешимы. Я считаю, что моя работа полезная и актуальная, изложена кратко и просто.
СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ
1. Википедия статья комплексные числа. https://ru.wikipedia.org/wiki/Комплексное_число (дата обращения: 08.01.2023)
2. Комплексные числа простыми словами. http://www.mathprofi.ru/kompleksnye_chisla_dlya_chainikov.html (дата обращения: 08.01.2023)
3. Лекция комплексных чисел. https://vk.com/doc672567631_652197675?hash=ZNijR77ifbebbxoeBgzO1ei4HhpWwppjRQLre7fZQts&dl=QjRzZkxds5V912zhiMaPMiZNDjLZyN7LXsW3WsrUbyg (дата обращения: 13.01.2023)
4. Википедия статья о числах. https://ru.wikipedia.org/wiki/Число (дата обращения: 15.01.2023)
5. История возникновения чисел и систем счисления. https://www.sites.google.com/site/istoriaciselisistemscislenia/istoria-vozniknovenia-cisel (дата обращения: 28.01.2023)
6. Тема 4. Комплексные числа Лекция 4. Комплексные числа. https://studfile.net/preview/7830079/ (дата обращения: 02.02.2023)
7. Шахмейстер А. Х. Комплексные числа; МЦНМО, Петроглиф, Виктория плюс - Москва, 2011.
8. Дадаян А.А., Новик И.А. Алгебра и начала анализа. - М.: Просвещение, 1987
9. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Шабунин М.Ш. Алгебра и начала анализа. Пробный учебник 9-10 классов средней школы. - М.: Просвещение, 1975.
10. Гордиенко Н.А., Беляева Э.С., Фирстов В.Е., Серебрякова И.В. Комплексные числа и их приложения: Учебное пособие. - Воронеж: ВГПУ, 2004.
10





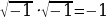
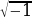 ,
, 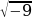 ,
, 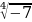 не имеют смысла и, поэтому, уравнения
не имеют смысла и, поэтому, уравнения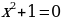 ,
, 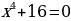 ,
, 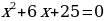
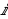
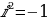
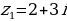
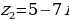
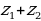 ;
; 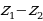 ;
; 

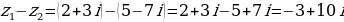

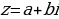 называется такое число, что
называется такое число, что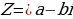 . То есть в сопряженном числе знак между действительной и мнимой частями всегда противоположен знаку того числа, с которым он сопряжен.
. То есть в сопряженном числе знак между действительной и мнимой частями всегда противоположен знаку того числа, с которым он сопряжен. 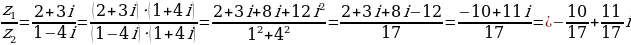
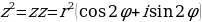
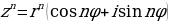
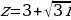 , найти
, найти 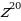
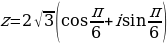
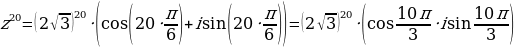
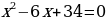
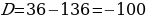
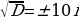
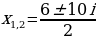
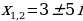 -сопряженные комплексные корни
-сопряженные комплексные корни 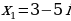 ,
,