© 2022, Никитина Марина Владимировна 3142 37
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 18.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 02.01.2025 17:34
Никитина Марина Владимировна
преподаватель математики и информатики
4 558
11 951 
Специализация
Индивидуальный проект "Жизнь и творчество Б. Паскаля"
Категория:
Математика
09.04.2022 15:12
Просмотр содержимого документа
«Индивидуальный проект "Жизнь и творчество Б. Паскаля"»
Министерство образования Тульской области
ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ТУЛЬСКОЙ ОБЛАСТИ
«ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ КОММУНАЛЬНО-СТРОИТЕЛЬНЫЙ ТЕХНИКУМ»
ИДИВИДУАЛЬНЫЙ ПРОЕКТ
ЖИЗНЬ И ТВОРЧЕСТВО БЛЕЗА ПАСКАЛЯ
Выполнил:
студент группы Д1-3 Д. А. Ткачёв
Проверил:
преподаватель М.В. Никитина
Тула 2021
Введение 3
1 Биография Б. Паскаля 4
2 Первые работы 7
3 Счетная суммирующая машина Паскаля 8
4 Треугольник Паскаля и его свойства 10
5 Вклад Паскаля в физику 13
6 Философские труды Блеза Паскаля 15
7 Результаты социологического опроса 18
Заключение 20
Список использованных источников 21
Математика появилась одновременно со стремлением человека изучить мир вокруг себя. Изначально она входила в состав философии - матери наук - и не была выделена как отдельная дисциплина наравне с той же астрономией, физикой. Однако с течением времени ситуация изменилась.
Актуальность темы: Блез Паскаль – выдающийся математик, физик, механик, философ, литератор. Стоял у истоков основания математического анализа, теории вероятности и проективной геометрии, создал первую счетную машину, прототип современного калькулятора, сформулировал основной закон гидростатики, автор нескольких философских сочинений.
Он обладал уникальной способностью проникать в самую суть вещей, и благодаря этому стать одним из величайших мировых ученых. Его литературные творения бессмертны, в них содержатся его мысли, высказывания, цитаты. Паскаль твердо верил в бесконечность предмета познания, и утверждал, что познаниям нет конца.
Проблема исследования: в какой мере научные труды Б. Паскаля повлияли на современную науку.
Цель исследования: изучение биографии Б. Паскаля
Задачи исследования:
- познакомиться с жизнью и творчеством Б. Паскаля,
-перечислить его научные труды;
- проанализировать вклад Б. Паскаля в развитие математики;
Объект исследования: биография Б.Паскаля
Предмет исследования: научные достижения Б.Паскаля в различных областях науки.
Методы исследования:
-поиск информации в сети Интернет;
- анализ литературных источников;
- обобщить и систематизировать теоретические сведения по теме;
- анализ данных социологического опроса;
Гипотеза: если бы в свое время Блез Паскаль не достиг таких успехов в науках, то человечество не находилось бы на таком уровне развития, который мы сейчас имеем.
Величие человека – в его способности мыслить.
Блез Паскаль
Блез Паскаль (рисунок 1) родился 19 июня 1623 года в городке Клермон-Ферран в центре Франции. Он был вторым ребенком в семье, кроме него родители воспитывали старшую дочь Жильберту и младшую Жаклин. Отца семейства звали Этьен Паскаль, он занимал должность председателя в налоговом управлении. Мама – Антуанетта Бегон, родом из богатой семьи сенешаля Оверни, занималась домом и воспитанием детей.
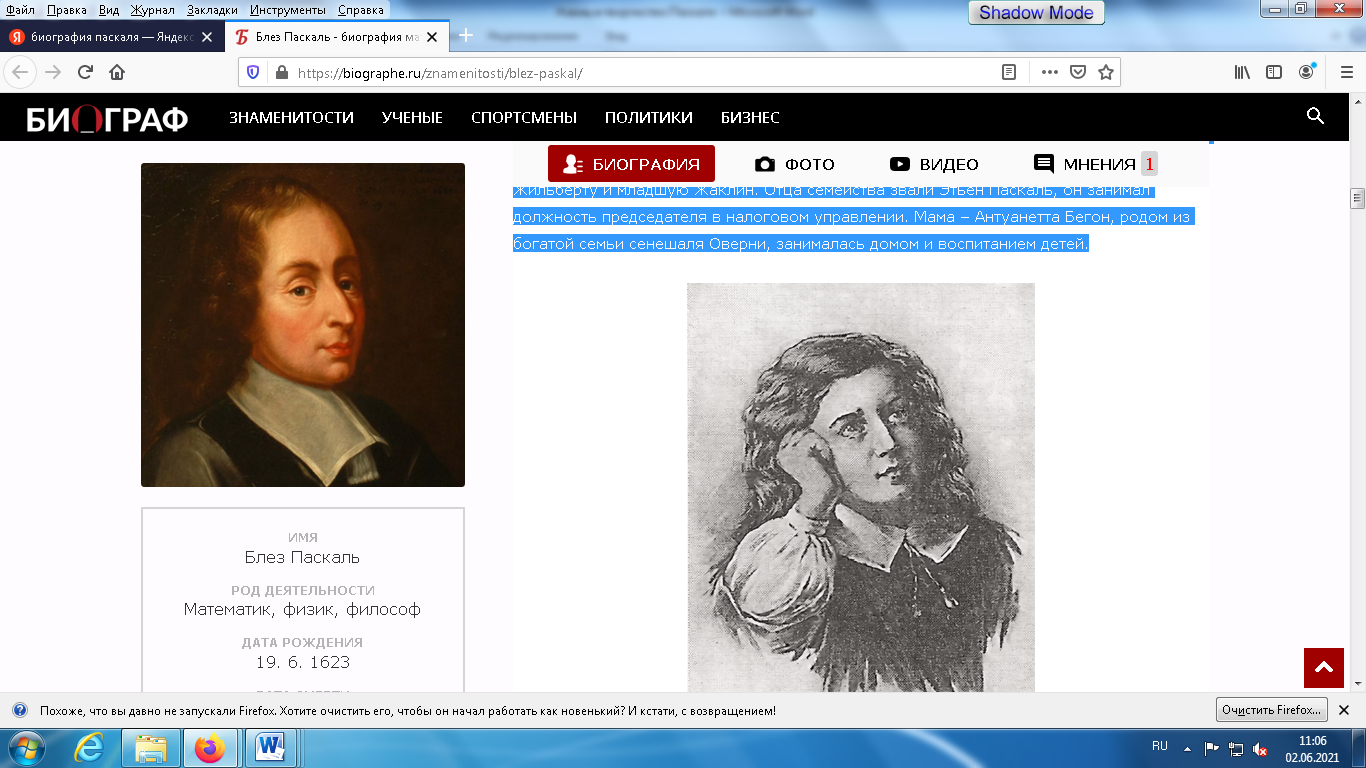
Рисунок 1- Блез Пскаль
Блез рос одарённым ребёнком. Отец самостоятельно занимался образованием мальчика, он сам неплохо разбирался в математике — дружил с Мерсенном и Дезаргом, открыл и исследовал неизвестную ранее алгебраическую кривую, с тех пор получившую название «улитка Паскаля», входил в комиссию по определению долготы, созданную Ришелье. Паскаль-отец придерживался принципа соответствия сложности предмета умственным способностям ребёнка. По его плану древние языки Блез должен был изучать с 12-ти, а математику с 15-16-летнего возраста. Метод обучения состоял в объяснении общих понятий и правил и последующем переходе к изучению отдельных вопросов. Так, знакомя восьмилетнего мальчика с законами грамматики, общими для всех языков, отец преследовал цель научить его мыслить рационально. В доме постоянно велись беседы по вопросам математики и Блез просил познакомить его с этим предметом. Отец, опасавшийся, что математика помешает сыну изучать латинский и греческий языки, обещал в будущем сделать это. Как-то раз, на очередной вопрос сына о том, что такое геометрия, отец кратко ответил, что это способ чертить правильные фигуры и находить между ними пропорции, однако запретил ему всякие исследования в этой области. Однако Блез, оставаясь один, принялся углём чертить на полу различные фигуры и изучать их. Не зная геометрических терминов, он называл линию «палочкой», а окружность «колечком». Когда отец случайно застал Блеза за одним из таких самостоятельных уроков, он был потрясён: мальчик, не знавший даже названий фигур, самостоятельно доказал 32-ю теорему Евклида о сумме углов треугольника. Тогда Паскаль-отец отказался от своего первоначального плана обучения и разрешил читать сыну математические книги. В часы отдыха Блез изучал Евклидову геометрию, позднее, с помощью отца, перешёл к работам Архимеда, Аполлония и Паппа, потом — Дезарга. Когда Блезу было 11 лет, кто-то за обеденным столом зацепил ножом фаянсовое блюдо. Оно зазвучало. Мальчик обратил внимание, что стоило прикоснуться к блюду пальцем, как звук исчез. Чтобы найти этому объяснение, Паскаль провёл серию опытов, результаты которых позднее изложил в «Трактате о звуках». С 14 лет Паскаль участвовал в еженедельных семинарах Мерсенна, проводимых по четвергам. Здесь он познакомился с Дезаргом. Юный Паскаль был одним из немногих, кто изучал его труды, написанные сложным языком и насыщенные новоизобретёнными терминами. Он совершенствовал идеи, высказанные Дезаргом, обобщая и упрощая обоснования. В январе 1640 года семья Паскалей переезжает в Руан. В эти годы здоровье Паскаля, и без того неважное, стало ухудшаться. Тем не менее он продолжал работать. Отец Блеза по роду службы в Руане часто занимался утомительными расчётами, сын также помогал ему в распределении податей, пошлин и налогов. Столкнувшись с традиционными способами вычислений и, находя их неудобными, Паскаль задумал создать вычислительное устройство, которое могло бы помочь упростить расчёты. В 1642 году (в 19 лет) Паскаль начал создание своей суммирующей машины «паскалины», в этом, по его собственному признанию, ему помогли знания, полученные в ранние годы.
Привычная жизнь Паскаля закончилась. Ухудшается и состояние его здоровья: врачи предписывают уменьшить умственную нагрузку. Паскаль бывает в обществе, завязывает светские отношения. Весной 1652 года в Малом Люксембургском дворце он свою арифметическую машину и ставил физические опыты, заслужив всеобщее восхищение. Машина Паскаля вызвала интерес у шведской королевы Кристины — по просьбе аббата Бурдело учёный преподнёс ей один экземпляр своего изобретения.
Самым близким из друзей-аристократов для учёного стал герцог де Роанне, увлекавшийся математикой. В доме герцога, где Паскаль подолгу жил, ему была отведена особая комната. Через Роанне Паскаль познакомился с богачом и страстным игроком Дамье Миттоном, эрудитом кавалером де Мере. Размышления, основанные на наблюдениях, сделанных Паскалем в светском обществе, позднее вошли в его «Мысли
У Паскаля множество планов на будущее. В письме Парижской академии (1654) он сообщил, что готовит фундаментальный труд под названием «Математика случая».
Отказавшись от систематических занятий наукой, Паскаль тем не менее изредка обсуждает математические вопросы с друзьями, но не собирается более заниматься научным творчеством. Единственным исключением стало фундаментальное исследование циклоиды (как рассказывали друзья, он занялся этой проблемой, чтобы отвлечься от зубной боли). За одну ночь Паскаль решает задачу Мерсенна о циклоиде и делает ряд открытий в её изучении.
С 1658 года здоровье Паскаля быстро ухудшается. Согласно современным данным, в течение всей жизни Паскаль страдал от комплекса заболеваний: рака мозга, кишечного туберкулёза, ревматизма. Его одолевает физическая слабость, появляются ужасные головные боли. Гюйгенс, посетивший Паскаля в 1660 году, нашёл его глубоким стариком, хотя Паскалю было всего 37 лет.
Осенью 1661 года Паскаль поделился с герцогом де Роанне идеей создания дешёвого и доступного всем способа передвижения в многоместных каретах. Герцог создал акционерное общество для реализации этого проекта и 18 марта 1662 года в Париже открылся первый маршрут общественного транспорта, названного впоследствии омнибусом (повозка на конной тяге, предшественник автобуса).
19 августа 1662 года после мучительной продолжительной болезни Блез Паскаль скончался. Похоронен в приходской церкви Открытия Паскаля до сегодняшнего дня служат в сфере гидравлики и вычислительной техники
Первое знаменательное событие в биографии молодого ученого случилось в 1640 году, когда ему исполнилось всего 17 лет. Паскаль издал свой первый трактат под названием «Опыт теории конических сечений» (рисунок 2), ставший основой для дальнейших разработок в геометрии. Третью лемму этого трактата назвали в честь ее создателя – теорема Паскаля. С ее помощью можно по пяти точкам построить каноническое сечение.
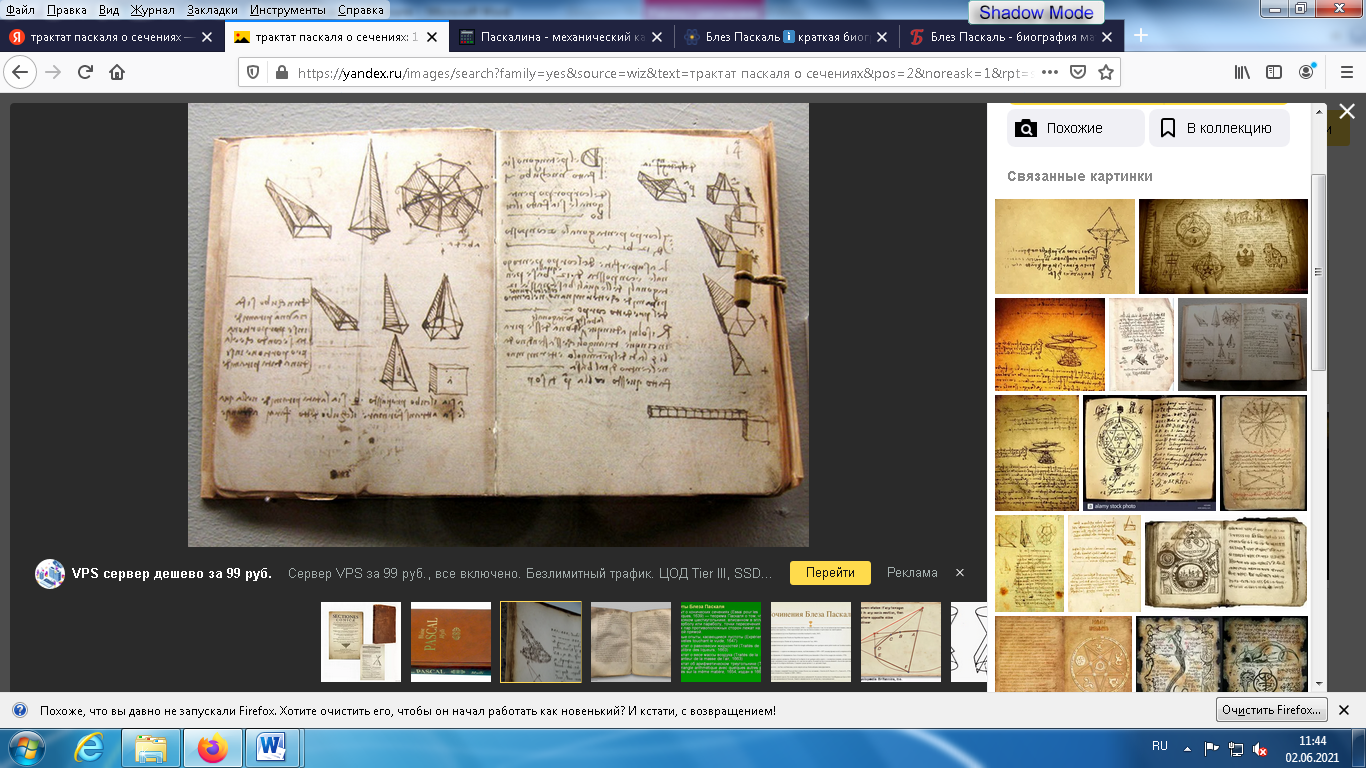
Рисунок 2 – Трактат «Опыт теории конических сечений»
В это сочинение автор включил теоремы (доказательства не приводятся), три определения, три леммы и указал главы планируемого труда, посвящённого коническим сечениям. Третья лемма из «Опыта…» является теоремой Паскаля: если вершины шестиугольника лежат на некотором коническом сечении, то три точки пересечения прямых, содержащих противоположные стороны, лежат на одной прямой. Этот результат и 400 следствий из него Паскаль изложил в «Полном труде о конических сечениях», о завершении которого Паскаль сообщил пятнадцать лет спустя и который сейчас отнесли бы к проективной геометрии. «Полный труд…» так и не был опубликован: в 1675 году его прочёл в рукописи Лейбниц, рекомендовавший племяннику Паскаля Этьену Перье срочно напечатать его. Однако Перье не прислушался к мнению Лейбница и впоследствии рукопись была утеряна.
Счетная суммирующая машина Блеза Паскаля – это изобретение, удивившее современников, но так и не нашедшее свой круг клиентов. Механизм, в основе имеющий зубчатые колесики, считается одним из прародителей калькулятора.
Паскаль уже в 19-летнем возрасте начал заниматься разработкой своей счетной машины, о которой сейчас можно прочитать на страницах учебников. Это изобретение считается одним из прообразов калькулятора.
«Паскалина» (рисунок 3) - это небольшой ящичек, в котором находится множество соединенных между собой зубчатых колесиков (шестеренок). На каждом колесике были разметки от нуля до девяти. Для того, чтобы произвести операцию сложения необходимо было набрать суммирующиеся числа с помощью нужного количества оборотов шестеренок. Колесики двигались до того момента, пока не появилось нужное число. При полном обороте появившейся остаток (больше 9) шестеренка перекидывала на другой разряд, передвигая соседнее колесо на одно деление.
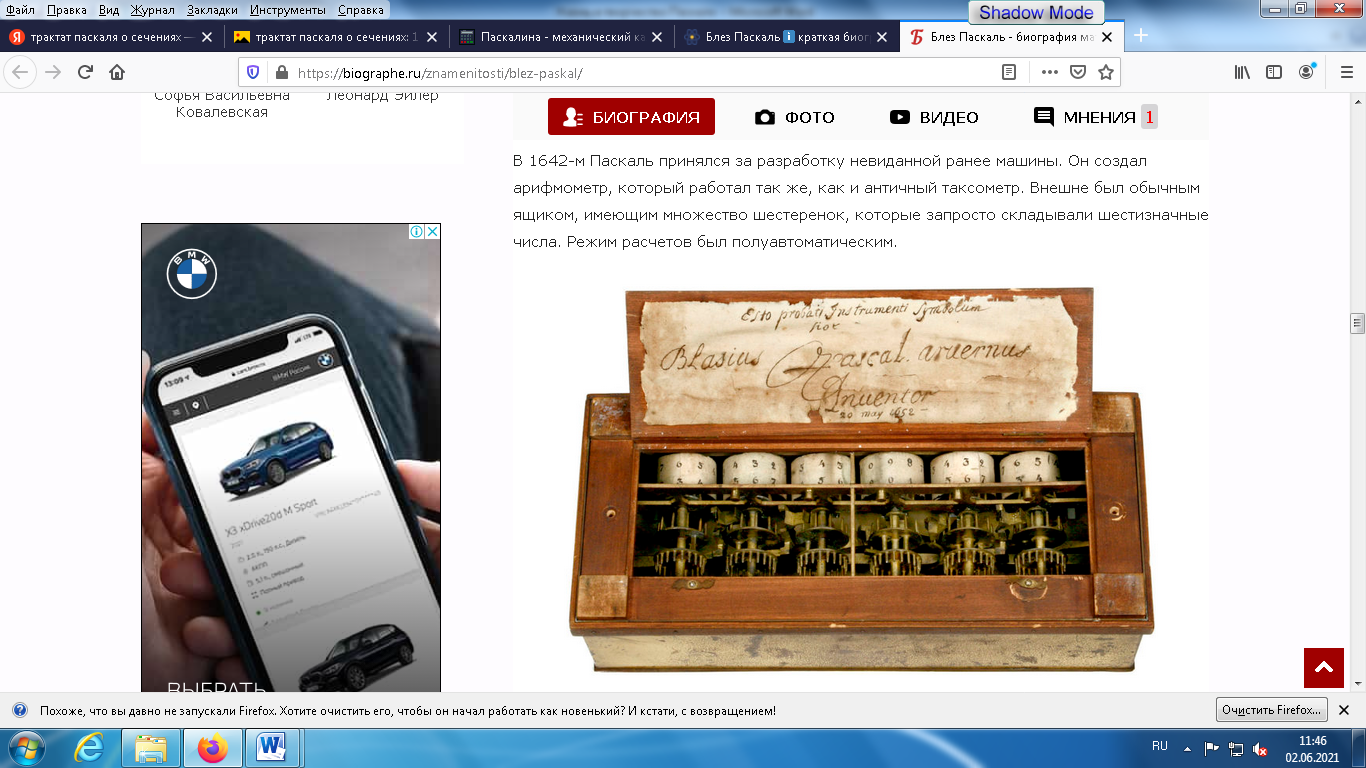
Рисунок 3 - Паскалина
В данной вычислительной машине колеса могли вращаться только в одном направлении. Производить суммирующие операции на такой машине было легко. Например, нам необходимо высчитать сумму 10+15=? Для этого необходимо вращать колесо пока не выставится значение первого слагаемого 10, потом крутим это же колесо до значения 15. При этом указатель сразу же показывает 25. То есть подсчет происходит в полуавтоматическом режиме.
Вычитание на такой машине невозможно произвести, так как колеса не вращаются в обратном направлении. Делить и умножать арифмометр Паскаля не умел. Но даже в таком виде и с такими функциональными возможностями эта машина была полезной и ей с радостью пользовался Паскаль-старший. Машина производила быстрые и безошибочные математические действия по суммированию вложил.
Использование оборотов колеса для процесса сложения не был новшеством в научной деятельности Паскаля, так как эту идею озвучил еще в 1623 году Вильгельм Шиккард. А действительно изобретением Блеза считается перенос остатка в следующий разряд при полном вращении шестеренки.
В первых «паскалинах» было по пять зубчатых колесиков, а уже с дальнейшей модернизацией технологии в механизме их число доходило до восьми штук, что позволяло работать с большими числами (до 9999999).
Этот механизм активно использовался в разных технических приборах до ХХ века. Его преимуществом было умение автоматического складывания многозначных чисел самим прибором.
Исследователи истории возникновения счетных механизмов считают, что Паскаль создал свою суммирующую машину практически с нуля, так как не был ознакомлен с проектом Шиккарда.
В 18 столетии арифмометры Паскаля широко использовались моряками, артиллеристами и ученными для арифметических сложений.
Прибор удивил современную науку, однако из-за высокой стоимости и сложности в эксплуатации так и не смог обрести свою аудиторию. Все же изобретение Паскаля внесло огромный вклад в историю развития вычислительной техники.
Треугольник Паскаля арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.
Если очертить треугольник Паскаля (рисунок 4), то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятности и обладает занимательными свойствами.
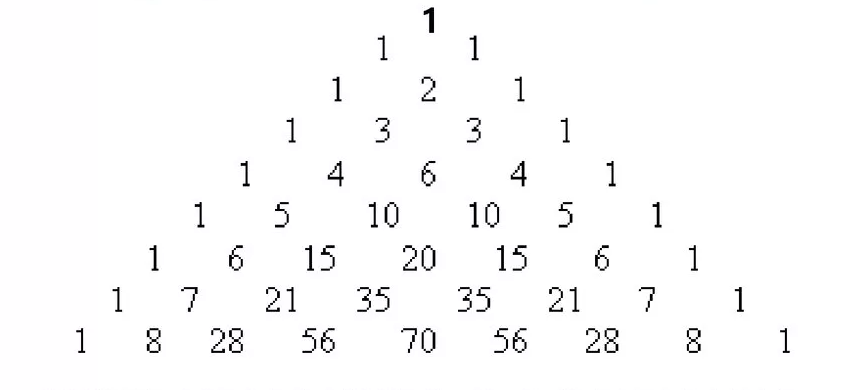
Рисунок 4 – Треугольник Паскаля
Мартин Гарднер пишет в книге "Математические новеллы" (М., Мир, 1974): "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике".
Треугольник Паскаля обладает следующими свойствами (рисунок 5)
Второе число каждой строки соответствует её номеру.
Третье число каждой строки равно сумме номеров строк, ей предшествующих.
Четвертое число каждой строки является тетраэдрическим.
Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.
Сумма чисел n-й строки треугольника Паскаля равна 2n
Простые делители чисел треугольника Паскаля образуют симметричные самоподобные структуры.
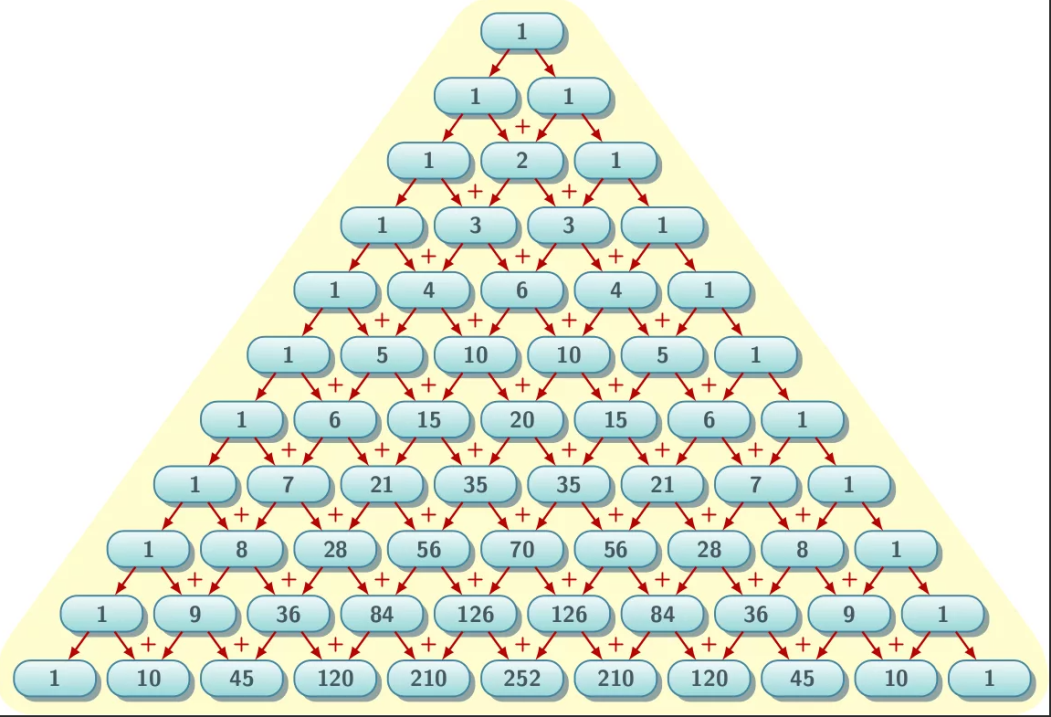
Рисунок 5 -Свойства треугольника
Треугольные числа в самом обычном и привычном нам виде показывают, сколько касающихся кружков можно расположить в виде треугольника - как классический пример начальная расстановка шаров в бильярде. К одной монетке можно прислонить еще две - итого три - к двум можно приладить еще три - итого шесть. Продолжая наращивать ряды с сохранением формы треугольника, получим ряд 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66..., что и показывает вторая зеленая линия. Этот замечательный ряд, каждый член которого равен сумме натурального ряда чисел (55=1+2+3+4+5+6+7+8+9+10), содержит также множество знакомцев, хорошо известных любителям математики: 6 и 28 - совершенные числа, 36 - квадратное число, 8 и 21 - числа Фибоначчи.
Биномиальные коэффициенты есть коэффициенты разложения многочлена по степеням x и y.
Каждая строчка имеет определенную структуру:
-
по краям стоят единицы
-
количество элементов в каждой строчке равно номеру строчки
-
каждый элемент строчки, кроме стоящих по краям равен сумме двух стоящих над ним.
В треугольнике представлены коэффициенты в разложении (a+b)n (рисунок 6). Номер строчки в этом треугольнике соответствует n+1. Теперь разберемся со степенями одночленов в разложении.
Степени всех одночленов, входящих в состав разложения равны n, причем степень первого слагаемого a уменьшается с n до 0, а степень второго слагаемого b увеличивается с 0 до n. Коэффициенты разложения совпадают с числами, стоящими в пятой строчке треугольника Паскаля.
Пользуясь треугольником Паскаля, мы можем возвести двучлен (a+b) в любую степень, не заучивая сложные формулы.
Рисунок 6 – Возведение многочлена в степень
Физикой Паскаль начал увлекаться в 1646 году, когда он узнал о трубке, которую изобрел Торричели. Блез начал проводить опыты и эксперименты, стремясь доказать на практике, что гипотеза Аристотеля о «боязне пустоты» ограничена определенными пределами. Проводя опыты с трубкой Торичелли – сосудом, заполненным ртутью – он доказал существование атмосферного давления, подтвердив существовавшие ранее гипотезы. Сам Паскаль писал, что с помощью такого прибора можно было бы узнать, как две разных точки земного шара смещены относительно друг друга. Эти исследования стали важным этапом усовершенствования барометров.
Продолжая развивать работы Симона Стевина и Галилео Галилея, Паскаль сформулировал закон о распределении давления в жидкой среде, получивший затем его имя. Выведенное им уравнение служит основой гидростатики. Кроме того, в своем трактате «О равновесии жидкостей» Блез впервые опубликовал идею гидравлического пресса. Изобретение долгое время оставалось невостребованным, и только в 1975 году английский инженер Джозеф Брама запатентовал прототип устройства.
Занимаясь проблемами физики, ученый сформулировал закон, который в настоящее время носит имя "закон Паскаля". В честь Блеза Паскаля была названа физическая единица 1Паскаль - единица измерения давления. Опыты Паскаля 1647 г. со столбами различных жидкостей доказали существование атмосферного давления. . Для проведения опытов Паскалю понадобилась помощь искусных стеклодувов, много вина, масла и воды и в придачу трехмачтовое судно, причем даже неизвестно, потребовалось ли этому судну отходить от причала. Ведь для опытов с этими жидкостями ученому были необходимы трубки длиной около 15 м, которые поддерживались в вертикальном положении привязанными к мачтам. В ходе проведенных экспериментов Паскалю удалось изобрести шприц и гидравлический пресс и усовершенствовать барометр. Увлекшись философией, Блез Паскаль продолжил учение Декарта о методе логического мышления, в "Письмах к провинциалу" остро критиковал иезуитов, склонялся к превосходству веры над разумом. Основное его философское сочинение "Мысли о религии" было издано в 1669 году. Блез Паскаль сравнивал Вселенную со сферой. Он писал о Вселенной как о не имеющей границ сфере, центр которой всюду, поверхность – нигде! Блез Паскаль считал, что эти три состояния разума и души могут описать отношение человека к любому явлению или к любой информации. Это - вера, отрицание и сомнение. Блез Паскаль писал: "Самые лучшие книги - те, при чтении которых каждый верил бы, что сам бы мог их написать ". Паскаль утверждал, что человек никогда не сможет стать счастливым, так как " мы никогда не живем, мы только надеемся жить и постоянно надеемся быть такими". Блез Паскаль говаривал: «Величие человека тем и велико, что он сознает свое ничтожество». Блез Паскаль говорил: "Не огромность мира звезд вызывает восхищение, а человек который этот мир измерил". Паскаль считает, что есть только три типа людей: одни обрели Бога и служат ему - эти люди разумны и счастливы. Другие же не нашли и не ищут Его - эти безумны и несчастны. Третьи не обрели, но ищут Его - эти люди разумны, но еще несчастны". Блез Паскаль назвал молчание "величайшим из человеческих страданий". Многие выдающиеся ученые прошлого стремились создать вечный двигатель. Не избежал этой участи и великий Блез Паскаль. Он рассматривал в качестве прообраза вечного двигателя груз, движущийся по тяжелому вращающемуся маховику. Однако в отличие от большинства других проектов перпетуум-мобиле, разработка Паскаля нашла выход в практику, правда, не для тех целей, для которых ее создавал автор. Это – рулетка казино. Паскаль, много занимавшийся теорией азартных игр, вывел "формулу игрока".
Блез Паскаль оставил след в истории как математик и физик, однако мало кто знает, что Паскаль отстранился от научной деятельности, отдав предпочтение философии.
Дело в том, что в 1654 году Блез Паскаль, который планировал написать трактат «Математика случая», решил отстраниться от светской жизни из-за озарения, случившегося в половину двенадцатого вечера. После бессознательного потока мысли пришедший в чувство Блез начал записывать на первом попавшемся кусочке пергамента свои идеи, зашив этот черновик в подкладку одежды. Эта запись, названная «Мемориалом» и изменившая судьбу ученого, была обнаружена только после смерти Паскаля.
Блез решил покинуть столицу Франции и сделаться духовником в монастыре Пор-Рояль, приравняв все светские связи, которые ранее давали ему надежду на счастливую жизнь, к греху. Паскаль был принят в обитель и стал придерживаться сурового образа жизни. Несмотря на тяжелый распорядок дня, малое количество сна и постоянные молитвы, ученый почувствовал улучшение здоровья и возвышение духа.
Помимо прочего, Блез Паскаль, после дискуссии с янсенистами и иезуитами, которые в духе рационализма излагали пропаганду моральных ценностей, создал «Письма к провинциалу». Трактат Паскаля, опубликованный под псевдонимом и осуждающий казуистику, вызвал скандал в общественности, поэтому ученый, рискуя попасть за решетку, вынужден был некоторое время скрываться и жить под чужой фамилией.
Основное философское произведение Блеза Паскаля носит название «Мысли» (рисунок 7) и представляет собой собрание коротких заметок и афоризмов, в которых он выразил свое отношение к природе и сущности человека.
Рисунок 7 – Книга «Мысли»
Однако этот знаменитый труд был издан только спустя несколько десятилетий после смерти автора, так как власть ранее вынесла приговор осуждения предыдущей книге Паскаля, направленной против иезуитов. Книга была публично сожжена, и это негативно отразилось на восприятии творчества Паскаля современниками. Этот факт позволил Ницше в середине XIX века писать о том, как христианство порой было жестоко по отношению к гениальным людям.
Для философии Паскаля наиболее характерным мотивом является стремление поставить в центр человека. Его чрезвычайно занимает вопрос, как мы можем получать истинное знание об окружающей нас реальности и о самих себе. Ответом на этот вопрос он считает особую возможность познания, а именно – так называемую «интуицию сердца». Именно сердце, как считает Паскаль, чувствует первичные аксиомы и термины, при помощи которых существует знание
Интуиция сердца обладает способностью выводить человека за пределы ограниченного мира обыденности, даже за пределы его разума, проблематичного и склонного к ошибкам. У сердца свои законы, считает философ, и они не совпадают с законами разума. Этот новый вид чувственной интуиции есть исходный пункт размышления, на который следует опираться каждому, кто стремится мыслить и искать истину. Помимо интуиции сердца, для Паскаля, как человека и как философа, очень важной является эмоциональная жизнь, которая, как он считает, дает истинное знание и истинное переживание происходящего.
Здесь, в сфере размышлений, касающейся человека и его сущности, перед Паскалем встает проблема бесконечности. Бесконечное для него – это то, что не в состоянии преодолеть человеческий рассудок, то, перед чем индивид пасует, находится в состоянии растерянности и страха. И только при помощи сердца и интуиции сердца мы можем осмыслить бесконечное, проникнуть в него взором, смириться с ним. Проявлением бесконечности в реальности для Паскаля является природа во всем ее многообразии. Поэтому изучение природы и своеобразное в чувствование в нее – это важный и существенный шаг на пути познания бесконечности.
Другой стороной бесконечности является та сложность, с которой устроен каждый живой организм, каждое существо и особенно человек. Как считает Паскаль, в каждом субъекте ведут войну разум и чувства. Разум считает, что только он способен познавать истину и открывать своему обладателю – человеку – тайные стороны реальности. Однако и чувства считают аналогично, стремясь дать истинное знание из собственного опыта. На самом же деле, они не должны конфликтовать между собой, так как знание, даруемое ими, взаимодополняемо и не является полным, существуя одно без другого. Взятые же по отдельности данные чувств и разума легко могут обмануть человека, оставить его в заблуждении.
Но даже то знание, которое возникает в результате соединения данных разума и информации, получаемой чувствами, не является безусловно истинным. Это происходит потому, что окружающий нас мир бесконечен и многообразен, а человек по сравнению с ним ничтожен, подобен крохотной песчинке на берегу океана. Паскаль называет его в своей книге «мыслящим тростником», имея в виду под этими словами хрупкость человеческого существа, колышемого ветром истории. Однако несмотря на свою хрупкость, человек наделен сознанием и стремлением к истине. Его постоянный интерес к происходящему вокруг позволяет хрупкому существу выживать в суровых природных условиях и не только сохранять жизнь, но и побеждать природу, становиться ее господином и повелителем.
Поэтому при всей своей ничтожности человек в то же время велик и могуществен. Он не может знать всего, но стремится к знанию, он не может пересилить стихию, но при помощи созданных своим гением приспособлений он преодолевает ее. Величие человека состоит также в том, что в основе его стремлений всегда лежат добро, красота и любовь. Ни одному другому существу на земле не дано понимание этих трех понятий. Поэтому только человек способен воплотить в жизнь множество прекрасных проектов, изменить мир и самого себя к лучшему.
Только человек может отрешиться от самолюбия и нести любовь другим людям и живым существам. Способность к любви, как считает Паскаль, является самой важной из человеческих способностей. Именно посредством любви мы можем жить и выживать, только через нее мы порождаем новые поколения и создаем произведения искусства, которыми будут восторгаться потомки спустя сотни лет. Только любящий индивид может разглядеть красоту в некрасивом, только любящий может творить добро без корысти и тайного умысла. Именно поэтому добродетель настоящей личности для Паскаля – это ненависть к себе как ничтожному существу и уважение себя как творящего добро, создающего красоту и дарящего любовь
Паскаль был очень впечатлительным человеком, который мог после какого-нибудь события, заставившего его пережить эмоциональное потрясение, по нескольку дней пребывать в состоянии ступора, не видя ничего вокруг и не обращая внимания на людей и происходящее.
В социальной сети «В контакте» мной был проведен социологический опрос по следующим вопросам:
1.Знаете ли вы, кто такой Б.Паскаль?
2 Что такое Паскалина?
3 Где применяется треугольник Паскаля?
. На вопрос «Знаете ли вы, кто такой Б.Паскаль?» были получены следующие результаты: 95% опрошенных ответили – физик, математик, философ и 5% опрошенных ответили нет.
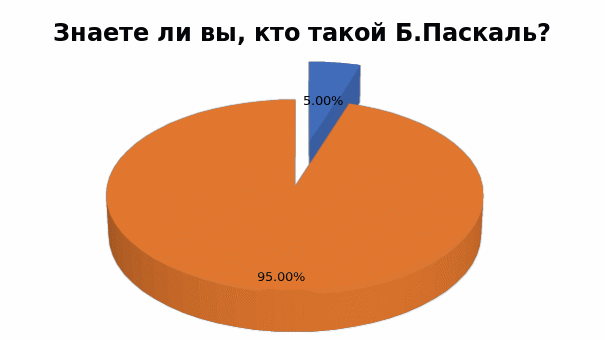
Рисунок 8
На вопрос, что такое Паскалина, 75% ответили не знают, что это, 20% сказали, что это счетное устройство, а 5% пояснили для чего оно использовалось.
Рисунок 9
На вопрос где применяется треугольник Паскаля (рисунок 10) 50% опрошенных ответили, что в какой-то математической формуле, 38% сказали, что первый раз слышат о таком треугольнике и лишь 12% опрошенных сказали, что данный треугольник используется для определении коэффициентов при возведении многочлена в степень.
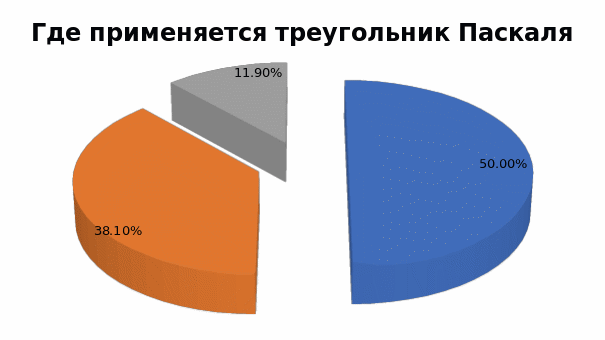
Рисунок10 ЗАКЛЮЧЕНИЕ Из века в век математика привлекала ученых своей неестественностью, которая удивительным образом могла описать все то, что происходит в мире вокруг нас.
Имена великих математиков - это не просто перечень людей, которые увлекались своим делом, расширяя и углубляя научную базу. Это звенья, которые способны связать настоящее и будущее, показать человечеству перспективу.
Научные открытия Б. Паскаля используют и по сей день.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
