муниципальное общеобразовательное учреждение
“Гимназия №1”
Информационно-исследовательский проект:
“Вневписанная в треугольник окружность”
Автор проекта:
Ученик 9 “В” класса
Муханов Матвей
Руководитель проекта:
Учитель математики
Бородкина Татьяна Ивановна
Железногорск
2018
Содержание:
1.Введение…………………………………………………………......3
2.Историческаясправка…………………….........................................4
3.Целипроекта……………………………………………………........5
4.Актуальность темы……………………………………………........5
5.Задачи проекта………………………………………………………5
6.Определение вневписанной окружности....……………………….6
7.Свойства вневписанной окружности….…………………………..7
7.1. Свойство 1…………………………………………………..7
7.2. Свойство 2…………………………………………………..8
7.3. Свойство 3…………………………………………………..9
7.4. Свойство 4…………………………………………………10
7.5. Свойство 5…………………………………………………11
8.Задачи на свойства вневписанной окружности……………….....12
8.1. Задача 1…………………………………………………….12
8.2. Задача 2…………………………………………………….13
8.3. Задача 3…………………………………………………….14
8.4. Задача 4……………………………………...………….15-16
8.5. Задача 5…………………………………………………….17
8.6. Задача 6…………………………………………………….18
9.Заключение…………………………………………………….......19
10.Список использованной литературы и Интернет-ресурсов.......20
Введение:
Чем же выделяется геометрия среди других разделов мaтематики? Во-первых, геометрия - это древнейшая наука. А термин «математика» появился относительно недавно, поэтому древние учёные, которые в нашем представлении занимались математикой, называли себя геометрами. Некоторые теоремы геометрии стали памятниками мировой культуры. Ярким примером является “Теорема Пифагора”, которая используется при доказательстве и решении большинства задач, связанных с прямоугольным треугольником.
Моя работа посвящается одному из интереснейших понятий геометрии, которое обычно остаётся в стороне из-за своей сложности. Речь идёт о вневписанной окружности. В этом проекте я собрал всю самую важную информацию об этой теме. Благодаря этому она станет проще для понимания.
Историческая справка
Многие из вас наверное знают про окружность девяти точек(она названа так, потому что проходит через три тройки точек: через основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с точкой пересечения высот). Эта окружность, найденная в XVIII в. великим ученым Л. Эйлером (поэтому ее часто также называют окружностью Эйлера), была заново открыта немецким математиком XIX века К. Фейербахом (братом известного философа).
Дополнительно К. Фейербах выяснил, что окружность девяти точек имеет еще четыре точки, тесно связанные с геометрией любого данного треугольника. Это – точки ее касания с четырьмя окружностями. Одна из этих окружностей вписанная, остальные три – ВНЕВПИСАННЫЕ. Таким образом, окружность девяти точек в действительности является окружностью тринадцати точек. Прямые в треугольнике, соединяющие его вершины с точками касания вневписанных окружностей, пересекаются в одной точке, которая называется точкой Нагеля в честь открывшего ее немецкого математика Августа Нагеля (1821-1903).
Цель проекта:
Ввести определение вневписанной окружности, рассмотреть её свойства и применить их при решении задач на вычисление и доказательство.
Актуальность темы:
Задачи на данную тему представлены на экзаменах в 9-х и 11-х классах. При их решении выпускники испытывают наибольшие затруднения. Многие из них даже не приступают к решению. Поэтому я хочу изучить свойства вневписанных окружностей и познакомить с ними старшеклассников, а также решить задачи на данную тему, предлагаемые на ОГЭ и ЕГЭ.
Задачи проекта:
Изучить математическую литературу по данной теме.
Ввести определение вневписанной окружности треугольника.
Рассмотреть свойства вневписанных окружностей треугольника.
Доказать свойства вневписанной окружности и показать её связь с элементами треугольника.
Показать применение свойств вневписанной окружности при решении задач на доказательство, построение и вычисление.
Вневписанная окружность:
Окружность называют вневписанной в треугольнике, если она касается одной из сторон треугольника и продолжений двух других сторон этого треугольника. Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных
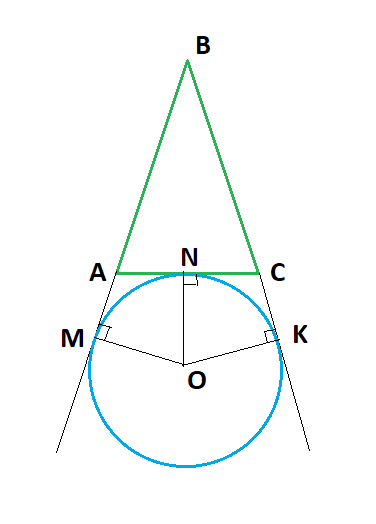
Свойства вневписанной окружности:
Свойство 1. Центр вневписанной окружности в треугольнике есть точка пересечений биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается и биссектрис двух внешних углов треугольника.
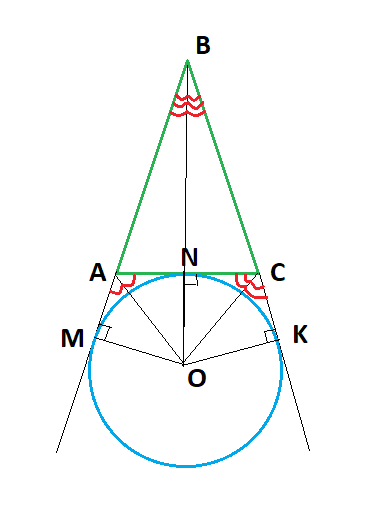
Доказательство:
Т.к. окружность касается сторон ∠CAM, то точка О - центр окружности равноудалённая от сторон этого угла, значит он лежит на биссектрисе ∠СAM. Аналогично, точка О равноудалена от сторон ∠ACK , значит О лежит на биссектрисе ∠ACK . Окружность касается прямых BA и BC, значит она вписана в ∠ABC, а следовательно центр лежит на биссектрисе ∠ABC.
Свойство 2. Расстояния от вершины угла треугольника до точки касания вневписанной окружности со сторонами этого угла равны полупериметру этого треугольника
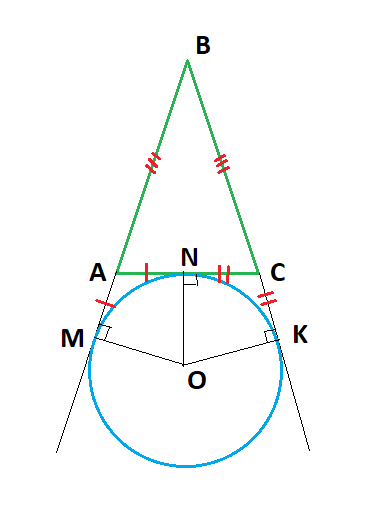
Докажем, что BM = BK= 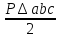
Доказательство:
О – центр вневписанной окружности. По свойству отрезков касательных, проведенных из одной точки, имеем: BM=BK, AM=AN, CN=CK. Значит 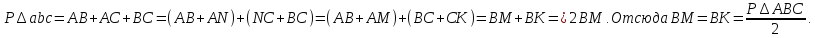
Свойство 3. Радиус вневписанной окружности, касающийся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны.
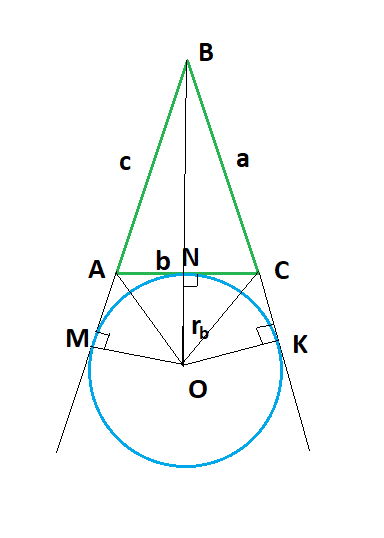
Докажем, что 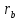 =
=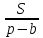
Доказательство:
Пусть AB=c, AC=b, BC=c, BM=BK=b .
S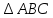 =S
=S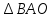 +S
+S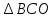 -S
-S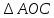 .Т.к.
.Т.к. 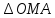 =
=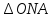 ,
, 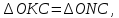
То S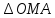 = S
= S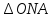 , S
, S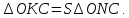 Значит S∆ABC= S
Значит S∆ABC= S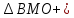
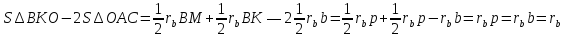 (p-b). Отсюда
(p-b). Отсюда 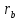 =
=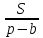 .
.
Свойство 4. Сумма всех попарных произведений радиусов вневписанных окружностей равна квадрату полупериметра треугольника.
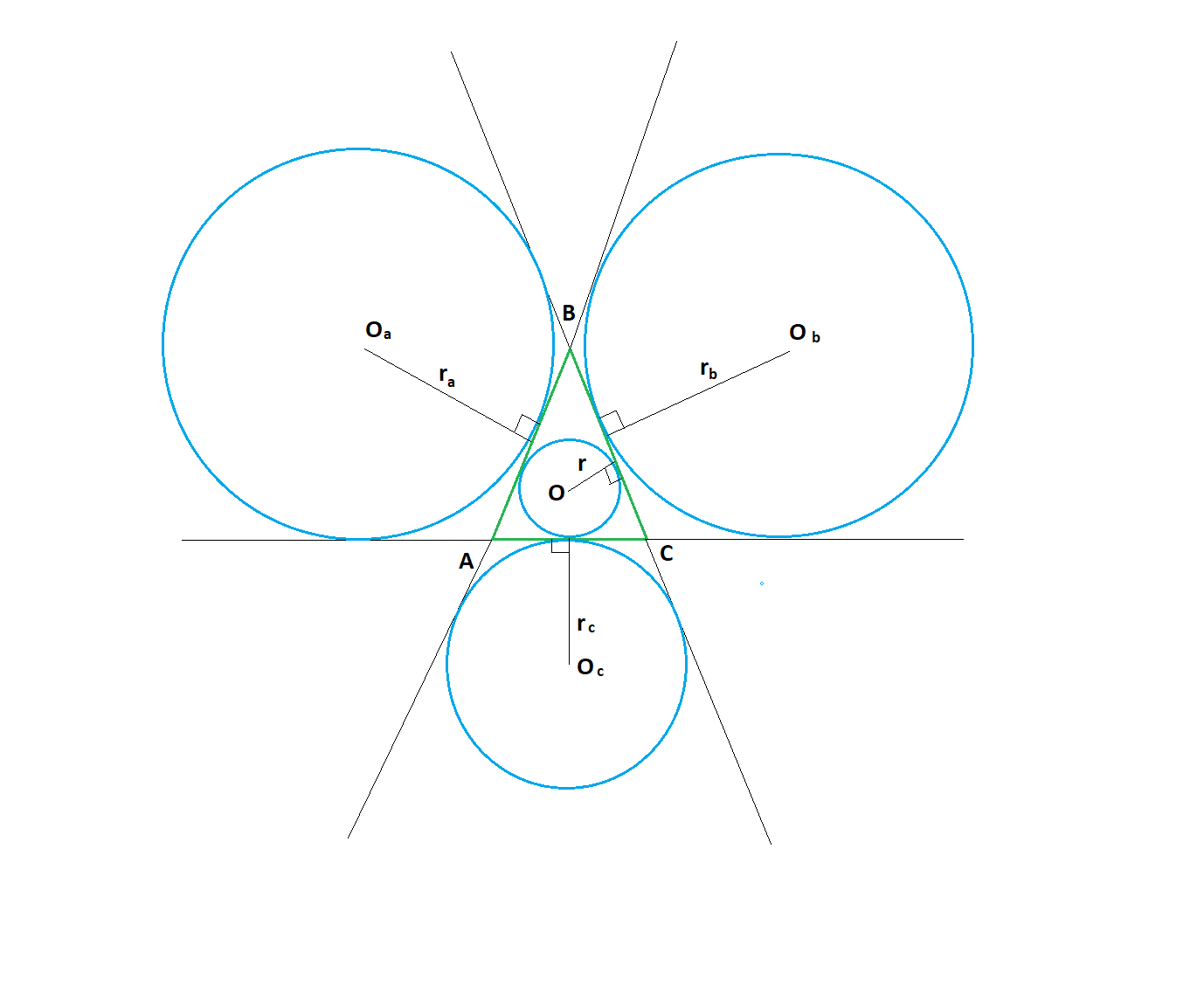 Докажем , что
Докажем , что 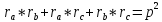
Доказательство:
Мы знаем : r =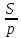 ;
; 
 ;
; 
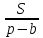 ;
; 
 .
.
Имеем, + = = = = = =  =
=  . (Заметим, что a+b+c=2p).
. (Заметим, что a+b+c=2p).
Свойство 5. Сумма величин, обратных радиусам вневписанных окружностей треугольника, равна обратному радиусу вписанной в этот треугольник окружности.

Докажем, что 
Доказательство:
Поскольку ,
, то
то  ,
, 
 . Складывая эти формулы и воспользовавшись формулой для радиуса окружности
. Складывая эти формулы и воспользовавшись формулой для радиуса окружности  , получим =
, получим = =
= Что и требовалось доказать.
Что и требовалось доказать.
Задачи на свойства вневписанной окружности
Задача 1. Условие: Дан ABC. Центры вневписанных окружностей O1, O2 и O3 соединены прямыми. Доказать, что  O1O2O3 — остроугольный.
O1O2O3 — остроугольный.
Решение: Центр O1 вневписанной окружности, касающейся стороны BC, является точкой пересечения биссектрис внешних углов при вершинах B и C. Поэтому
∠ O1CB =  и ∠ O1BC =
и ∠ O1BC =  . Следовательно, ∠BO1C =
. Следовательно, ∠BO1C =  o.
o.
Задача 2. Условие: Докажите, что прямая, проходящая через центры вневписанных окружностей треугольника ABC, касающихся сторон AB и AC, перпендикулярна прямой, проходящей через центр вписанной окружности и вершину A.
Решение: Пусть O1 и O2 – центры вневписанных окружностей треугольника ABC, касающихся сторон AB и AC соответственно; O — центр вписанной окружности треугольника ABC. Поскольку точкиO1 и O2 расположены на биссектрисах вертикальных углов с вершиной A, то прямая O1O2 проходит через точку A. ∠ O1AO – это угол между биссектрисами смежных углов, поэтому ∠O1AO = 90°.
Задача 3. Условие: Дан равнобедренный треугольник ABC с основанием AC. Доказать, что конец D отрезка BD, выходящего из вершины B, параллельного основанию и равного боковой стороне треугольника, является центром вневписанной окружности треугольника.
Решение: BD – биссектриса внешнего угла ∠ B .Треугольник CBD – равнобедренный, поэтому ∠GCD = ∠BDC = ∠DCB (G – точка на продолжении отрезка AC за точку C), то есть CD – биссектриса ∠ C. D –точка пересечения биссектрис BD и CD , она, как известно, является центром вневписанной окружности.
Задача 4. Условие: Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание. б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?
Решение:
а) Вневписанной окружностью называется окружность, которая касается стороны треугольника и продолжений двух других его сторон. Пусть угол ∠А = ∠С = α, так как треугольника ∆АВС — равнобедренный. Угол ∠DBC – внешний угол треугольника ∆АВС, поэтому ∠DBC = ∠А + ∠С = 2α.Окружность касается сторон угла ∠DBC, значит, ВО – биссектриса угла ∠DBC, т. е. угол ∠DBО = ∠ОBC = α.Получаем, что ∠DBО = ∠А = α. Соответственные углы ∠DBО и ∠А при пересечении прямых ВО и АМ секущей AD равны, то прямые ВО и АМ параллельны. BH – высота треугольника ∆АВС, следовательно, BH перпендикулярна АМ. АМ – 15 касательная к окружности, следовательно, ОМ перпендикулярна АМ (ОМ – радиус окружности). Значит, ВН параллельна ОМ. Получаем, ВОМН – прямоугольник. Следовательно, радиус окружности равен высоте треугольника, опущенной на основании, т. е. R = BH.
б) Пусть радиус вневписанной окружности ОМ = R, а радиус вписанной в треугольник окружности QK = QH = r. Тогда по условию R = 4r. Треугольники ∆АВН и ∆QВК – подобные треугольники (∠В – общий, ∠ВКQ = ∠ВНА), следовательно,
 AB=
AB=
BH = OM = R = 4r QB = BH – QH = 4r – r = 3r
Из прямоугольного треугольника ∆QBK по теореме Пифагора найдем BK:
BK2 = QB2 – KQ2 =(3r)2 – r2 = 8 . BK = 2√2r.
. BK = 2√2r.
AB= AK = AB – BK=3√2r – 2√2r = √2r. Тогда отношение, в котором точка касания вписанной окружности с боковой стороной треугольника делит эту сторону, равно Ответ:  .
.
Задача 5. Условие: Найдите периметр треугольника ABC, если расстояние от вершины A до точки касания с вневписанной окружностью равно 17, расстояние от вершины B до точки касания окружности со стороной BC равно 6, расстояние от вершины C до точки касания окружности со стороной AC равно 4.
Решение:
1)Рассмотрим 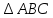
a) Т.к. BL=B =6 (как отрезки касательный, проведенных из одной точки), то AB=A
=6 (как отрезки касательный, проведенных из одной точки), то AB=A -B
-B = AB=17-6=11. b) Т.к. CL=C
= AB=17-6=11. b) Т.к. CL=C =4 (как отрезки касательный, проведенных из одной точки), то BC=BL+LC = BC=6+4=10. c) Т.к. A
=4 (как отрезки касательный, проведенных из одной точки), то BC=BL+LC = BC=6+4=10. c) Т.к. A =A
=A =17(как отрезки касательный, проведенных из одной точки), то AC=A
=17(как отрезки касательный, проведенных из одной точки), то AC=A -C
-C = AC=17-4=13
= AC=17-4=13
2) P=AB+BC+AC = P=11+10+13=34 Ответ: 34.
Задача 6 Условие: Найдите радиус вневписанной окружности треугольника, если радиусы двух других вневписанных окружностей равны 2002 и 4004, а радиус вписанной окружности равен 1001.

Решение:
Т.к. сумма величин обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, а именно
 , то составим равенство:
, то составим равенство: =
=
 =
=  .
.
Ответ: .
.
Заключение:
1.Изучив свойства вневписанной окружности, я:
А)Кратко изложил понятия, приводящие к пониманию вневписанной окружности
Б)Доказал её свойства и применил их к решению геометрических задач.
2.Работая над данной темой, я научился лучше рассуждать, анализировать и систематизировать данные. Надеюсь, что опыт выполнения этой работы пригодится вам в будущем. Данный материал выходит за рамки школьной программы и будет полезен учащимся при подготовке к ЕГЭ и ОГЭ.

Список литературы и Интернет-ресурсов:
https://www.uchmet.ru/library/material/142952/91879/
5









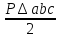
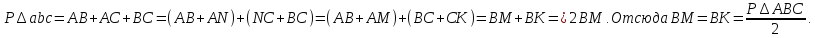

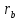 =
=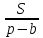
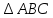 =S
=S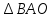 +S
+S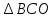 -S
-S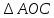 .Т.к.
.Т.к. 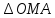 =
=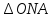 ,
, 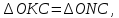
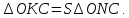 Значит S∆ABC= S
Значит S∆ABC= S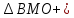
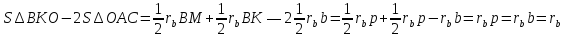 (p-b). Отсюда
(p-b). Отсюда  Докажем , что
Докажем , что 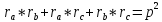
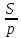 ;
; 

















