Приложение 3
Районная научно – практическая конференция «Шаг в науку».
Группа «Юниор».
Информационный сборник
«ПРИЗНАКИ ДЕЛИМОСТИ НАТУРАЛЬНЫХ ЧИСЕЛ»
Авторы: Аксененко София, Калугина Дарья.
пос. Карымское, Забайкальский край
2018 г.
Приложение 3
Содержание:
Стр.
Признаки делимости, изучаемые в школьной программе. 3
Классификация признаков делимости. Свойства делимости. 4 - 5
Признак Паскаля. 6 - 7
Библиографические сведения. 8
Доказательство некоторых признаков делимости. 9 - 10
Сводная таблица признаков делимости. 11 - 12
Примеры с решением. 13 - 15
Задачи с решением. 16 - 19
Примеры и задачи для самостоятельного решения. 20 - 24
Список использованной литературы. 25
Интернет – ресурсы. 25
Старинная притча. 26
1.
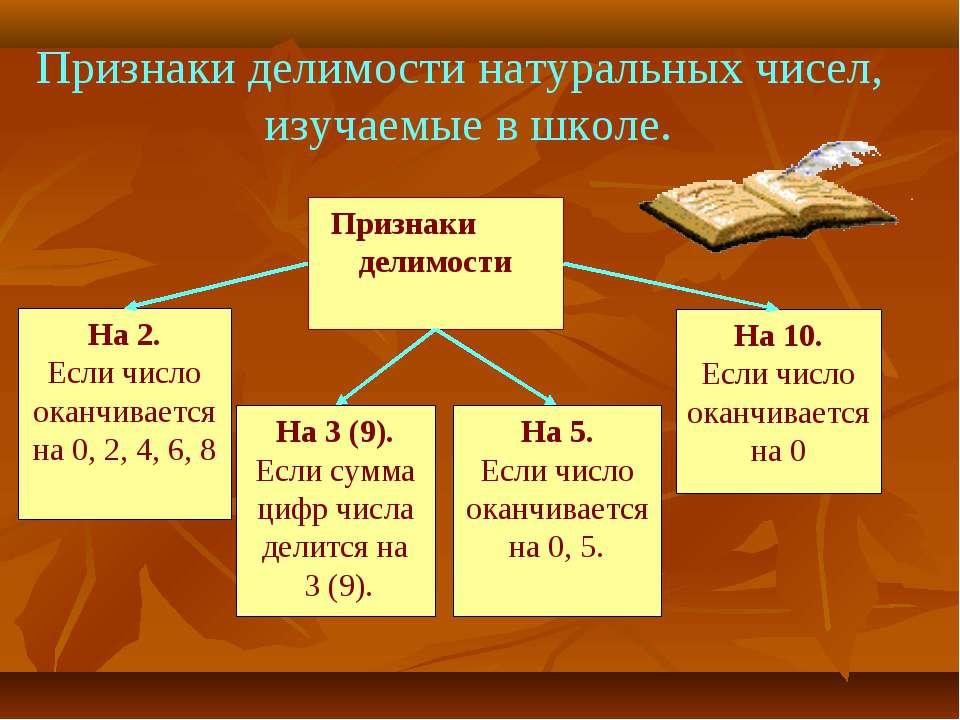
Классификация признаков делимости. Свойства делимости.


Признак Паскаля.
Натуральные числа можно записать в виде суммы разрядных слагаемых. Например, число 756 = 6*1 + 5*10 + 7*102; число 2354 = 4*1 + 5*10 + 3*102 + 103;
2835102 = 2*1 + 1*102 + 5*103 + 3*104 + 8*105 + 2*106 и т.д.
Вообще, если мы имеем некоторое (n + 1) – значное число А, то его можно записать в виде А = a0*1 + a1*10 + a2*102 + … + an*10n, где a0, a1, a2, …, an – его разрядные единицы. Установим делимость натурального числа А на натуральное число b ≠ 1. Пусть q0 и r0, q1 и r1, q2 и r2, …, qn и rn – соответственно частные и остатки от деления чисел 1 = 100, 10, 102, …, 10n на b (0 ≤ rn ˂ b).
Тогда
1 = bq0 + r0,
10 = bq1 + r1,
102 = bq2 + r2,
………………
10n = bqn + rn и
А = a0* (bq0 + r0) + a1* (bq1 + r1) + a2* (bq2 + r2) + ... + an* (bqn + rn), или, учитывая q0 = 0, имеем:
A = b (a1q1 + a2q2 + … + anqn ) + (a0r0 + a1r1 + … + anrn).
Первое слагаемое в правой части равенства делится на b. Поэтому если А делится на b, то и второе слагаемое делится на b. Наоборот, если второе слагаемое делится на b, то и А делится на b. Это и есть «признак Паскаля»: если число А делится на число b ≠ 1, то сумма a0r0 + a1r1 + … + anrn делится на b; если сумма a0r0 + a1r1 + … + anrn делится на b, то и А делится на b.
Пример.
Не выполняя деления, установим, делится ли число 5641713 на число 29.
r0 = 1, r1 = 10, r2 = 13, r3 = 14, r4 = 24, r5 = 8, r6 = 22.
Число 3*1 + 1*10 + 7*13 + 1*14 + 4*24 + 6*8 + 5*22 = 372 не делится на число 29,
то и число 5641713 не делится на число 29.
Пример.
Не выполняя деления, установим, делится ли число 2835102 на число 6.
r0 = 1, r1 = 4, r2 = 4, r3 = 4, r4 = 4, r5 = 4, r6 = 4.
Число 2*1 + 0*4 + 1*4 + 5*4 + 3*4 + 8*4 + 2*4 = 78 делится на число 6,
то и число 2835102 делится на число 6.
Таким образом «признак Паскаля» сводится к вычислению суммы a0r0 + a1r1 + … + anrn.
Пример.
Пусть b = 2, тогда r0 = 1, r1 = r2 = …= rn = 0, и поэтому a0*1 + a1*0 + a2*0 + … + an*0 = a0.
Число делится на 2, если оно четно, т.е. последняя его цифра делится на 2. Получаем признак делимости на 2.
Пример.
Пусть b = 9, тогда r0 = r1 = r2 = …= rn = 1 и поэтому a0*1 + a1*1 + a2*1 + … + an*1 = a0 + a1 + a2 + … + an. Это сумма цифр числа А. Она и определяет признак делимости числа А на 9.
Пример.
Пусть b = 11, тогда r0 = 1, r1 = 10, r2 = …= rn-1 = 1, rn = 10, и мы имеем:
a0*1 + a1*10 + a2*1 + … + an-1*1 + an*10 = (a0 + a2 + … + an-1) + 10*( a1 + a3 + … + an) в случае четного количества цифр делимого. Если в делимом нечетное количество цифр, то в первой скобке в равенстве будет на одно слагаемое больше, чем во второй.
Попробуем упростить полученное равенство. Замечаем, что при делении чисел 10, 103, 105, … на 11 остаток равен 10, то есть не хватает единицы до числа, делящегося на 11. Эту недостающую единицу попробуем взять со знаком «минус». Обозначив недостатки через rn’, вместо выражения a0*1 + a1*10 + a2*1 + … + an-1*1 + an*10 = (a0 + a2 + … + an-1) + 10*( a1 + a3 + … + an) получаем
(a0 + a2 + … + an-1) - ( a1 + a3 + … + an). Данное соотношение можно определить как признак делимости на 11.
На 11 делится число, в котором разность между суммами цифр, стоящих на четных и нечетных местах, делится на 11.
4. Библиографические сведения.
Блез Паскаль.

Блез Паскаль – один из самых знаменитых людей в истории человечества. Паскаль умер, когда ему было 39 лет, но, несмотря на столь короткую жизнь, вошел в историю как выдающийся математик, физик, философ и писатель. Паскаль родился 19 июня 1623 года в Клермон-Ферран, в семье высокообразованного юриста. Отец Паскаля имел хорошее образование и решил самостоятельно заниматься образованием мальчика. Блез рос одарённым ребёнком и рано проявил выдающиеся математические способности. Его отец старался обучить мальчика древним языкам, настаивая, чтобы тот не отвлекался «на разного рода пустяки». Как-то раз, на очередной вопрос сына о том, что такое геометрия, отец кратко ответил, что это способ чертить правильные фигуры и находить между ними пропорции. Однако тут же запретил ему всякие исследования в этой области. Но запретный плод сладок, и Блез, закрывшись в своей спальне, принялся углем выводить на полу различные фигуры и изучать их. Когда отец случайно застал его за одним из таких самостоятельных уроков, он был потрясен: не знавший даже названий фигур, мальчик доказывал их свойства. Так постепенно раскрывался гений Блеза Паскаля.
Отец Блеза был сборщиком налогов, и, наблюдая за его бесконечными утомительными расчетами, Паскаль, в возрасте 19 лет, задумал создать вычислительное устройство, которое могло бы помочь этой работе. Он работал над этим устройством в течение трех лет. Устройство, называющееся "Паскалиной", выглядело как ящик, наполненный многочисленными связанными друг с другом шестерёнками. Складываемые числа вводились соответствующим поворотом колес. За несколько лет Паскаль построил около 50 вариантов своей машины. Паскаль получил лично от короля Патент на изобретение с сохранением авторских прав на ее изготовление и продажу. Несмотря на вызываемый «Паскалиной» всеобщий восторг, машина не принесла богатства своему создателю. Однако изобретённый Паскалем принцип связанных колёс почти на три столетия стал основой создания большинства вычислительных устройств. Во Франции она оставалась в употреблении до 1799г., а в Англии даже до 1971 года.
5. Доказательство некоторых признаков делимости.
Признаки делимости на составное число.
Чтобы узнать, делится ли заданное число на составное, нужно разложить это составное число на взаимно простые множители, признаки делимости которых известны. Взаимно простые числа - это числа, не имеющие общих делителей кроме 1.
Например, число делится нацело на 15, если оно делится нацело на 3 и на 5. Рассмотрим другой пример составного делителя: число делится нацело на 18, если оно делится нацело на 2 и 9. В данном случае нельзя раскладывать 18 на 3 и 6, поскольку они не являются взаимно простыми, так как имеют общий делитель 3. Убедимся в этом на примере. Число 456 делится на 3, так как сумма его цифр равна 15, и делится на 6, так как оно делится и на 3 и на 2. Но если разделить 456 на 18 вручную, то получится остаток. Если же для числа 456 проверять признаки делимости на 2 и 9, сразу же видно, что оно делится на 2, но не делится на 9, так как сумма цифр числа равна 15 и она не делится на 9.
Признак делимости на 8.
Умножая многозначные натуральные числа на 8, заметим такую закономерность, числа, являющиеся произведением, оканчиваются на три нуля или три их последние цифры составляют число, которое делится на 8.
Значит, признак деления на 8 может быть таким:
Натуральное число делится на 8 тогда и только тогда, когда три его последние цифры 0 или составляют число, делящееся на 8.
Проверим: число 45000:8 = 5625. 96008:8= 12001.
Объединенный признак делимости на 7, 11 и 13.
Число делится на 7, 11 или 13, если алгебраическая сумма чисел, образованных тройками цифр данного числа в десятичной записи с чередующимися знаками делится соответственно на 7, 11 или 13.
Заметим, что произведение чисел 7, 11 и 13 равно 1001. Поэтому число 1000 при делении на 7, 11 или 13 равноостаточно с –1. Далее поступаем как и в признаке делимости на 11.
В качестве примера рассмотрим число 286 = 623 – 295 - 42 делится на 11 и 13, но не делится на 7. Следовательно, и данное число делится на 11 и 13, но не делится на 7.
Признак делимости на 37.
Число делится на 37, если сумма чисел, образованных тройками цифр данного числа в десятичной записи делится соответственно на 37.
Доказательство вытекает из того, что число 1000 при делении на 37 равноостаточно с 1.
Заметим также, что трехзначные числа 111, 222, …, 999 делятся на 37.
Признак делимости на 101.
Разобьем число на группы по 2 цифры справа налево ( в самой левой группе может быть одна цифра) и найдем сумму этих групп с переменными знаками, считая их двузначными числами. Эта сумма делится на 101 тогда и только тогда, когда само число делится на 101.
Например: 590547 делится на 101, так как 59 – 05 + 47 = 101 делится на 101, значит и число 590547 делится на 101.
Усовершенствованный признак делимости на 7
Чтобы проверить, делится ли число на 7, надо от числа отбросить последнюю цифру и от получившегося результата эту цифру дважды отнять. Если результат делится на 7, то и само число делится на 7.
6. Сводная таблица признаков делимости чисел
| Число  | Число а делится на число b тогда и только тогда, когда |
| 2 | Последняя цифра числа  делится на 2 делится на 2 |
| 3 | Сумма цифр числа  делится на 3 делится на 3 |
| 4 | Число, составленное из двух последних цифр числа  , делится на 4 , делится на 4 |
| 5 | Число  оканчивается цифрой 0 или 5 оканчивается цифрой 0 или 5 |
| 6 | Число  делится на 2 и на 3 делится на 2 и на 3 |
| 7 | Знакочередующаяся сумма трёхзначных граней* числа  делится на 7 делится на 7 |
|
| Если результат вычитания удвоенной последней цифры числа из этого числа без последней цифры делится на 7, то и само число делится на 7. |
| 8 | Число, составленное из трёх последних цифр числа  , делится на 8 , делится на 8 |
| 9 | Сумма цифр числа  делится на 9 делится на 9 |
| 10 | Число  оканчивается цифрой 0 оканчивается цифрой 0 |
| 11 | Знакочередующаяся сумма цифр числа  делится на 11 делится на 11 |
|
| На 11 делится число, в котором разность между суммами цифр, стоящих на четных и нечетных местах, делится на 11. |
| 12 | Число  делится на 3 и на 4 делится на 3 и на 4 |
| 13 | Знакочередующаяся сумма трёхзначных граней*  делится на 13 делится на 13 |
|
| Если разность числа тысяч и числа, образованного последними тремя цифрами, делится на 13, то и само число делится на 13. |
| 25 | Число, составленное из двух последних цифр числа  , делится на 25 , делится на 25 |
| 19 | Если в натуральном числе число его десятков, сложенное с удвоенным числом единиц, делится на 19, то и само число делится на 19. |
|
|
|
|
|
|
|
|
|
7. Примеры с решением.
1. Является ли 13 делителем числа 116519?
Решение: В числе 116519 последние три цифры образую число 519, а оставшиеся 116.
Найдем разность 519 – 116 = 403.
Чтобы узнать делится ли оно на 13, найдем сумму его десятков и учетверённое число единиц: 40 + 4 * 3 = 52.
Число 52 делится на 13, а, значит, 13 является делителем 116519.
Ответ: Да.
2. Делится ли число 110213608442 на 7?
Решение:
Найдем суммы
 110 + 608 = 718
110 + 608 = 718
213 + 442 = 655
и разность полученных результатов
718 – 655 = 63.
Число 63 делится на 7, а значит и 110213608442 делится на 7
Ответ: Да.
3. Делится ли число 175 на 7?
Решение:
В числе 175 имеется 17 десятков и 5 единиц, поэтому найдем следующую сумму
17 * 3 + 5 = 56,
а число 56 делится на 7. Следовательно число 175 делится на 7.
Ответ: Да.
4. Не выполняя деления, установим, делится ли число 5641713 на число 29.
Решение:
r0 = 1, r1 = 10, r2 = 13, r3 = 14, r4 = 24, r5 = 8, r6 = 22.
Число 3*1 + 1*10 + 7*13 + 1*14 + 4*24 + 6*8 + 5*22 = 372 не делится на число 29,
то и число 5641713 не делится на число 29.
5. Не выполняя деления, установить, делится ли число 543675 на 11.
Решение:
Вычислим суммы цифр числа, стоящие на четных и нечетных местах, и найдем их разность.
5 + 6 + 4 = 15, 7 + 3 + 5 = 15, 15 – 15 = 0, 0 делится на 11, значит, число 543675 делится на 11.
6. Не выполняя деления, установим, делится ли число 2835102 на число 6.
r0 = 1, r1 = 4, r2 = 4, r3 = 4, r4 = 4, r5 = 4, r6 = 4.
Решение:
Число 2*1 + 0*4 + 1*4 + 5*4 + 3*4 + 8*4 + 2*4 = 78 делится на число 6,
то и число 2835102 делится на число 6.
7. Трёхзначное число при делении на 10 даёт в остатке 3. Если последнюю цифру числа перенести в начало его записи, то полученное число будет на 72 больше первоначального. Найдите исходное число.
Решение:
Для удобства назовем наше число abc, где каждая буква обозначает конкретный разряд числа: a – сотни, b – десятки и c – единицы. По условию задачи при делении на 10 числа в остатке получается 3. Это возможно только в одном случае: если число заканчивается на 3, то есть c = 3, а число на данный момент равно ab3. Если перенесем последнюю цифру в начало, то получим число 3ab. Прибавим к числу ab3 число 72 столбиком и получим результат:
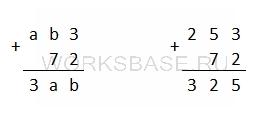
Цифры a и b вычисляются достаточно быстро. В разряде единиц к 3 прибавляем 2 и получаем, что b = 5. Заменяем все b в примере. В разряде десятков к найденному b прибавляем 7 и получаем 12. Таким образом,
а = 2, а единица переходит в разряд сотен, так как разряд десятков переполнен. Заменили в примере все a и убедились, что если к 2 прибавить единицу, которая перешла из разряда десятков, получится 3. Таким образом, искомое число равно 253.
ОТВЕТ: 253
8. Число яблок в ящике меньше 200. Их можно разделить поровну между 2,3,4,5 и 6 детьми. Какое максимальное количество яблок может быть в ящике?
Решение.
НОК(2,3,4,5,6) = 60.
60х
Ответ: 180 яблок.
9. Можно ли 2006 представить как разность квадратов двух натуральных чисел?
Если бы 2006 = a2 – b2 = (a – b)(a + b), то или a – b или a + b было бы четным числом. Но тогда и другое число было бы четным, а значит, a2 – b2 делилось бы на 4. Но 2006 не делится на 4.
Ответ. Нет.
8. ЗАДАЧИ с решением.
1. Найдите четырёхзначное натуральное число, меньшее 1360, которое делится на каждую свою цифру и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
РЕШЕНИЕ: Для удобства назовем наше число abcd, где каждая буква обозначает конкретный разряд числа: a – тысячи, b – сотни, c – десятки и d – единицы. По условию задачи abcd ⇒ число равно 1264, c = 7: 74 не делится на 4, c = 8: 84 / 4 = 21 ⇒ число равно 1284, c = 9: 94 не делится на 4. Если число равно 1264, оно должно делиться на 6 (быть четным, и сумма цифр числа должна делиться на 3). Число является четным, однако сумма цифр равна 13, и она не делится на 3. То есть число 1264 не подходит. Если число равно 1284, оно должно делиться на 8 (число, составленное из 3 последних цифр, должно делиться на 8). 284 на 8 нацело не делится. То есть число 1284 не подходит. Если d равно 6, текущее число равно 12c6. Чтобы число делилось на 6, нужно, чтобы оно было четным, и сумма цифр делилась на 3. Число четным является, сумма цифр числа равна: 1 + 2 + c + 6 = c + 9. Получается, что цифра c может быть равна 3 или 9, тогда сумма цифр будет делиться на 3 (6 не подходит, так как уже d = 6). Если c = 3, число равно 1236, оно должно делиться на 3, то есть сумма цифр числа должна делиться на 3. Сумма цифр числа равна 12, она делится на 3, значит, число 1236 подходит в качестве ответа. Если c = 9, число равно 1296, оно должно делиться на 9, то есть сумма цифр должна делиться на 9. Сумма цифр числа равна 18, она делится на 9, значит, число 1296 подходит в качестве ответа. Если d равно 8, текущее число равно 12c8. Чтобы число делилось на 8, нужно чтобы число 2c8, составленное из 3 последних цифр, делилось на 8. Не забываем, что цифры в числе не могут повторяться. Таким образом, c может быть равно: c = 3: 238 не делится на 8, c = 4: 248 / 8 = 31 ⇒ число равно 1248, c = 5: 258 не делится на 8, c = 6: 268 не делится на 8, c = 7: 278 не делится на 8, c = 9: 298 не делится на 8. Если число равно 1248, оно должно делиться на 4. Так как это число делится на 8, то оно делится и на 4 (4 является множителем для 8). Значит, число 1248 подходит в качестве ответа. Пусть b равно 3, тогда в данный момент число равно 13cd. Чтобы число делилось на 3, нужно чтобы сумма цифр числа делилась на 3. Сумма цифр числа равна: 1 + 3 + c + d = 4 + c + d. Цифра c может быть равна 2, или 4, или 5 (не больше, так как число должно быть меньше 1360, а цифры 1 и 3 уже использованы). Если c равно 2, текущее число равно 132d. Текущая сумма цифр равна 6 + d. Чтобы число делилось на 2, нужно чтобы оно было четным. Значит d может быть равно: d = 4: число равно 1324, сумма цифр равна 10, не делится на 3,
d = 6: число равно 1326, сумма цифр равна 12, делится на 3, d = 8: число равно 1328, сумма цифр равна 14, не делится на 3. Если число равно 1326, оно должно делиться на 6. Чтобы число делилось на 6, нужно, чтобы оно было четным, и сумма цифр делилась на 3. Число является четным, сумма цифр на 3 делится. Значит, число 1326 подходит в качестве ответа. Если c равно 4, текущее число равно 134d. Текущая сумма цифр равна 8 + d. Чтобы число делилось на 4, нужно, чтобы число 4d, составленное из 2 последних цифр, делилось на 4.То есть, d может быть равно 8 (цифра 4 уже используется, 0 использовать нельзя по условию). Однако сумма цифр числа равна 16, и она не делится на 3. Значит, это число не подойдет в качестве ответа. Если c равно 5, текущее число равно 135d. Текущая сумма цифр равна 9 + d. Чтобы число делилось на 5, нужно чтобы оно заканчивалось на 5 или 0. Однако, по условию в числе не может быть цифры 0, а цифра 5 уже использована. Таким образом, в ответе можно указать одно из следующих чисел: 1236, 1248, 1296 или 1326.
ОТВЕТ: 1236, или 1296, или 1248, или 1326.
2. Найдите натуральное число, большее 1340, но меньшее 1640, которое делится на каждую свою цифру и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
Решение: Для удобства назовем наше число abcd, где каждая буква обозначает конкретный разряд числа: a – тысячи, b – сотни, c – десятки и d – единицы. По условию задачи 1340
В данном случае сумма цифр равна: 1 + 3 + c + d = 4 + c + d. Чтобы попадать в интервал, нужно, чтобы c было равно 4, 5, 6, 7, 8 или 9. Если c равно 4, число будет равно 134d. Сумма цифр будет равна 8 + d. Чтобы число делилось на 4, нужно, чтобы число 4d, составленное из 2 последних цифр, делилось на 4. На 4 делятся числа 40, 44 или 48. Цифра d может быть равна только 8, так как по условию 0 не может быть в числе, а 4 уже есть в числе. Если d равно 8, число равно 1348, сумма цифр равна 16, она не делится на 3, поэтому число не подойдет. Если c равно 5, число будет равно 135d. Чтобы число делилось на 5, оно должно заканчиваться на 0 или 5, но ни то, ни другое невозможно. Если c равно 6, число будет равно 136d. Сумма цифр будет равна 10 + d. Чтобы число делилось на 6, оно должно быть четным и делиться на 3. Значит, d может быть равно 2, 4 или 8 (6 уже использовано, 0 нельзя использовать). Если d равно 2, число равно 1362, сумма его цифр равна 12 и она делится на 3. Также это число является четным. Таким образом, число делится на каждую свою цифру и может быть указано в качестве ответа. Если d равно 4, число равно 1364, сумма его цифр равна 14, она не делится на 3. Если d равно 8, число равно 1368, сумма его цифр равна 18 и она делится на 3. Также это число должно делиться на 8, для этого число 368, составленное из 3 последних цифр, должно делиться на 8. Оно делится на 8, значит, это число можно указать в качестве ответа. Если c равно 7, число будет равно 137d. Сумма его цифр будет равна 11 + d. Попробуем подобрать такую цифру d, чтобы сумма цифр делилась на 3. А уже потом разделим получившееся число на 7 для проверки. Цифра d может быть равна только 4 ( 1 и 7 уже использованы), так как сумма будет равна 15, и она делится на 3,число равно 1374. Чтобы оно делилось на 4, нужно, чтобы число, составленное из 2 последних цифр, делилось на 4, а 74 на 4 не делится. То есть число 1374 не подойдет. Если c равно 8, число будет равно 138d. Сумма цифр числа будет равна 12 + d. Чтобы число делилось на 8, нужно, чтобы число 38d делилось на 8. Значит цифра d может быть равна 4 (384/8 = 48). В этом случае число равно 1384. Сумма его цифр равна 16, она не делится на 3, значит число не подойдет. Если c равно 9, число будет равно 139d. Сумма цифр числа будет равна 13 + d. Чтобы число делилось на 9, нужно чтобы сумма его цифр делилась на 9. Цифра d в данном случае может быть равна только 5. Если число равно 1395, сумма его цифр также делится и на 3. Число также должно делиться на 5, то есть заканчиваться на 5. Это условие также соблюдается. Значит, число 1395 подойдет в качестве ответа. Пусть b равно 4, тогда в данный момент число равно 14cd. Чтобы число 14cd делилось на 4, нужно чтобы число cd делилось на 4.
Подберем возможные числа cd, чтобы в них не было цифр 1,4 и 0 и цифры были разными, которые будут делиться на 4: 28, 32, 36, 52, 56, 68, 72, 76, 92, 96. Пусть итоговое число равно: 1428: оно делится на 2, так как четное. Но 428 не делится на 8, значит и само число на 8 не делится. 1432: оно делится на 2, так как четное. Сумма цифр числа равна 10, она не делится на 3. Значит и число 1432 на 3 не делится. 1436: достаточно проверить, делится ли оно на 6, так как 3 является множителем у 6. Число делится на 6, если оно делится на 2 и на 3. Число четное (делится на 2), а сумма цифр равна 14, она не делится на 3. 1452 или 1456: оно не делится на 5, так как заканчивается не на 5. 1468: оно четное (делится на 2), сумма цифр равна 19, она не делится на 3. Значит, число на 6 не делится. 1472: оно делится на 2, так как четное. Однако число не делится нацело на 7. 1476: оно четное, сумма цифр равна 18, значит, число делится на 6. Однако это число не делится на 7. 1492: оно делится на 2, так как четное. Сумма цифр числа равна 16, она не делится на 9. 1496: сумма цифр числа равна 20, она не делится на 9. Пусть b равно 5, тогда в данный момент число равно 15cd. Чтобы число делилось на 5, нужно чтобы оно заканчивалось на 5 или 0. Число не может заканчиваться на 0 по условию задачи, а также цифра 5 не может повторяться в числе. Пусть b равно 6, тогда в данный момент число равно 16cd. Чтобы число делилось на 6, нужно чтобы число было четным и сумма цифр числа делилась на 3. В данном случае сумма цифр равна: 1 + 6 + c + d = 7 + c + d. Чтобы попадать в интервал, нужно, чтобы c было равно 2 или 3. Если c равно 2, число будет равно 162d. Сумма цифр числа равна 9 + d. Значит, d может быть равно 3 или 9 (чтобы сумма делилась на 3). Однако ни тот, ни другой вариант не подойдет, так как число должно быть четным. Если c равно 3, число будет равно 163d. Сумма цифр числа равна 10 + d. Значит, d может быть равно 2, 5 или 8 (чтобы сумма делилась на 3). Цифра 5 не подойдет, так как число не будет четным. Этим мы сразу же проверили делимость числа на 3 и на 6. Осталось проверить цифры 2 и 8. Если число равно 1632, оно является четным (делится на 2), значит, его можно указать в качестве ответа. Если число равно 1638, то нужно проверить, делится ли оно на 8. Однако на 8 оно не делится, так как 638 на 8 нацело не делится. Таким образом, в ответе можно указать одно из следующих чисел: 1362, 1368, 1395 или 1632. Достаточно было получить первое число и закончить на этом решение, но мы показали, как можно отыскать все возможные варианты.
ОТВЕТ: 1362, или 1368, или 1395, или 1632.
3.Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое – нибудь одно такое число.
Решение: Раскладываем делитель – число 12 на простые множители. 12 = 3 * 2 * 2. Делаем вывод, что заданное число после вычеркивания цифр должно делиться на 2, 2 и 3. На два делятся четные числа, следовательно, вычеркиваем цифру 1 в конце числа. Останется 18161512. Но нам нужно, чтобы искомое число делилось на 2 дважды, то есть на 4. Признак делимости на 4 утверждает, что для этого на 4 должно делиться двузначное число, образованное последними двумя цифрами. 12:4 = 3, поэтому две последние цифры числа 18161512 вычеркивать нельзя. Они гарантируют делимость числа на обе двойки.
Чтобы число делилось на 3, нужно, чтобы сумма цифр числа делилась на 3. 1+8+1+6+1+5+1+2 = 25, 25 = 3*8 + 1 – можно вычеркнуть одну из единиц, но по условию задачи нужно вычеркнуть еще две цифры. 25 = 3*7 + 4 – нет двух цифр для вычеркивания, сумма которых равнялась бы 4, так как последние цифры 1 и 2 трогать нельзя. 25 = 3*6 + 7 – сумма двух вычеркнутых цифр будет равна 7, если вычеркнуть цифру шесть и любую из цифр 1, кроме последней. Итак, возможные ответы 811512 или 181512. Выбираем один из вариантов и записываем ответ.
4. Вычеркните в числе 85417627 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите ровно одно получившееся число.
Решение: Чтобы заданное число 85417627 делилось на 18, нужно чтобы оно делилось на 2 и на 9. Чтобы число делилось на 2, оно должно быть четным. Чтобы число делилось на 9, сумма его цифр должна делиться на 9. Число 85417627 четным не является. Чтобы оно стало четным, из него нужно вычеркнуть последнюю цифру 7. Осталось вычеркнуть 2 цифры. После этого получилось число 8541762. Найдем сумму его цифр: 8 + 5 + 4 + 1 + 7 + 6 + 2 = 33 Чтобы число делилось на 9, сумма его цифр должна составлять 27 или 18 или 9. Число 27 отличается от 33 на 6 — это 4 + 2 или 5 + 1. Если вычеркнуть цифры 4 и 2, новое число 85176 останется четным и сумма его цифр равна 27, поэтому оно делится нацело на 18. Если вычеркнуть цифры 5 и 1, новое число 84762 останется четным и сумма его цифр равна 27, поэтому оно также делится нацело на 18. В качестве ответа можно выписать любое из них. Число 18 отличается от 33 на 15 — это 8 + 7. Если вычеркнуть цифры 8 и 7, новое число 54162 останется четным и сумма его цифр равна 18, поэтому оно делится нацело на 18. И это число также подойдет в качестве ответа. Сумму цифр числа, равную 9, получить вычеркиванием двух цифр не получится.
ОТВЕТ: 85176, или 84762, или 54162
9. Примеры и задачи для самостоятельного решения.
1. Найдите наименьшее трёхзначное число, которое при делении на 2 даёт остаток 1, при делении на 3 даёт остаток 2, при делении на 5 даёт остаток 3 и которое записано тремя различными нечётными цифрами.
2. Будет ли число 6375 делиться на 15?
3. Записать, используя по одному разу цифры 0, 1, 4, 7, наибольшее и наименьшее четырехзначные числа, кратные 15.
4. Найдите наименьшее трёхзначное число, которое при делении на 2 даёт остаток 1, при делении на 3 даёт остаток 2, при делении на 5 даёт остаток 3 и которое записано тремя различными нечётными цифрами.
5. Приведите пример трёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
6. Найдите наименьшее пятизначное число, кратное 55, произведение цифр которого больше 50, но меньше 75.
7. К числу 26 допиши левее и правее по цифре, чтоб полученное число было кратным 45.
8. Маугли попросил своих друзей – обезьян принести ему орехов. Обезьяны набрали поровну орехов и понесли Маугли. Но по дороге поссорились, и каждая обезьяна бросила в каждую по ореху. В результате Маугли достались лишь 35 орехов. По сколько орехов обезьяны собрали, если известно, что каждая из них принесла больше одного ореха?
9. Не выполняя деления, установить, делится ли число 352835 на 7.
10. Покупатель взял в магазине пакет молока, стоимостью 34,5 рубля, коробку творога, стоимостью 36 рублей, 6 пирожных и 3 килограмма сахара. Когда кассир выбила чек на 296 рублей, покупатель потребовал проверить расчет и исправить ошибку. Как определил покупатель, что счёт неверен?
11. Докажите, что произведение любых трех последовательных натуральных чисел делится на 6.
12. Не выполняя вычитания, установите, делится ли разность на 9.
а) 360- 144; 6) 946-540; в) 30240-97.
13. Не выполняя сложения, установите, делится ли значение выражения на 4:
а) 284 + 1440 + 113; в) 284 + 1441+ 113;
б) 284+ 1440 + 792224; г) 284+ 1441 + 113+ 164.
14. Записать, используя по одному разу цифры 0, 1, 4, 7, наибольшее и наименьшее четырехзначные числа, кратные 15.
15. Туристическое агентство «Дуремар» предложило Карабасу три путевки «в страну Дураков» - две взрослые и одну детскую за 3543 золотые монеты. Известно, что детская путевка на 500 золотых монет дешевле. Каким образом Карабас смог понять, что его обманывают?
16. У одного гражданина было 7 друзей.
Первый посещал его каждый вечер, второй - каждый второй вечер, третий - каждый третий вечер, четвертый – каждый четвертый вечер и так до седьмого друга, который являлся каждый седьмой вечер.
Часто ли случалось, что все семеро друзей встречались у хозяина в один и тот же вечер? (Решается с использованием признаков делимости на 2, на 3, на 4, на 5, на 6, на 7).
17. Ваня задумал простое трехзначное число, все цифры которого различны. На какую цифру оно может заканчиваться, если его последняя цифра равна сумме первых двух. Приведите примеры таких чисел.
18. Катя утверждает, что она придумала признак делимости на 81: «Если сумма цифр числа делится на 81, то и само это число делится на 81.» Верно ли Катино утверждение? Если да, то докажите его. Если нет, приведите пример опровергающий пример Кати.
19. Вовочка написал в тетради число 65349*0712 в качестве примера числа, которое делится: а) на 9; б) на 3. (На месте звёздочки когда-то была написана цифра, а теперь там пятно от сладкого чая.) Помогите Вовочке восстановить пропущенную цифру. Укажите все возможные варианты!
20. В магазин привезли меньше 600, но больше 500 тарелок. Когда стали раскладывать их десятками, то не хватило трех тарелок до полного числа десятков, а когда стали раскладывать по 12 тарелок, то осталось 7 тарелок. Сколько было тарелок?
21. Если из задуманного трехзначного числа вычесть .Если из задуманного трехзначного числа вычесть 7, то полученная разность разделится на 7, если вычесть 7, то полученная разность разделится на 7, если вычесть 8, то полученная разность разделится на 8; если вычесть 8, то полученная разность разделится на 8; если вычесть 9, то полученная разность разделится на 9. Какое 9, то полученная разность разделится на 9. Какое наименьшее из возможных чисел задумано? наименьшее из возможных чисел задумано?
22. Вычеркните в числе 51488704 три цифры так, чтобы получившееся число делилось на 15. В ответе укажите ровно одно получившееся число.
23. Приведите пример четырёхзначного числа, кратного 12, произведение цифр которого равно 10. В ответе укажите ровно одно такое число.
24. Приведите пример трёхзначного числа А, обладающего следующими свойствами: 1) сумма цифр числа А делится на 6; 2) сумма цифр числа А+3 также делится на 6; 3) число А больше 350 и меньше 400. В ответе укажите ровно одно такое число.
25. Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из первого числа вычли второе и получили 1458. Приведите ровно один пример такого числа.
26. Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 6 прыжков, начиная прыгать из начала координат?
27. Пять участников олимпиады стали её победителями, набрав по 15, 14, 13 баллов и заняв соответственно первое, второе и третье места. Сколько участников завоевали каждое призовое место, если вместе они набрали 69 баллов?
28. Сколько имеется четырёхзначных чисел, которые делятся на 45, а две средние цифры у них 97?
29. Ученики 5 класса купили 203 учебника. Каждый купил одинаковое количество книг. Сколько было пятиклассников, и сколько учебников купил каждый из них?
30. Напишите какое – нибудь девятизначное число, в котором нет повторяющихся цифр (все цифры разные) и которое делится без остатка
на 11. Напишите наибольшее из таких чисел, наименьшее из них.
31. Перед походом за покупками у Матроскина и Шарика денег было поровну. Матроскин израсходовал в 8 раз меньше денег, чем Шарик, а осталось у него в 9 раз больше денег, чем у Шарика. Доказать, что изначально количество денег у Матроскина делилось на 71 (имеется в виду, что у Матроскина и Шарика во всех ситуациях было целое количество денег).
32. К числу 10 слева и справа припишите по 1 цифре так, чтобы число делилось на 72.
33. Найдите наибольшее натуральное число, кратное 36, в записи которого участвуют все цифры по 1 разу.
34. Крестьянка несла на базар в корзине яйца. Проезжающий мимо всадник нечаянно толкнул ее, и все яйца разбились. На вопрос, сколько было яиц, она ответила: «Когда я их раскладывала по 2, то одно яйцо осталось. То же самое произошло, когда я их раскладывала по 3, по 4, по 5 и по 6. Когда я их разложила по 7, то остатка не оказалось». Сколько было яиц у крестьянки?
35. Докажите, что число 49100 – 1450 кратно 5.
36. Доказать, что 9110+4210 – 8510 кратно 10.
37. Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, или в 10 раз больше, или в 10 раз меньше предыдущего. Сумма всех членов последовательности равна 1860.
38. Найдите наибольшее шестизначное число в записи которого есть только цифры 1 и 5 и оно делится на 3 и на 5.
39. Найти наименьшее число, которое при делении на 2 дает остаток 1, при делении на 3 - 2, на 4 - 3, на 5 - 4, на 6 - 5, на 7 - 6, на 8 - 7, на 9 - 8, на 10 – 9.
40. На складе имеются ножи и вилки. Общее число тех и других больше 300, но меньше 400. Если ножи и вилки вместе считать десятками или дюжинами, то в обоих случаях получается целое число десятков и целое число дюжин. Сколько было ножей и вилок на складе, если ножей было на 160 меньше, чем вилок?
10. Список использованной литературы.
Булавко И. Делимость чисел.– Квант для младших школьников, №9, 1974. Лепёхин Ю. В. Олимпиадные задания по математике. 5 – 6 классы – Волгоград: Учитель, 2011. – 236 с.
Сергеев И.Н. Примени математику. - М.:1989.
Энциклопедический словарь юного математика. А. П. Савин М:Педагогика,1985-352с.
Математика. Школьная энциклопедия. С.М. Никольский.- М: Большая Российская энциклопедия: Дрофа 1997-527с.
Делимость чисел. Простые и составные числа. Генрих Г.Н. ФМШ №146 г. Пермь.
Московские математические олимпиады 1993 – 2005 г. Под редакцией . – М.: МЦНМО, 2006.
11. Интернет- ресурсы.
1. http://festival.1september.ru/2004_2005/index.php?numb_artic=213063-
2. Источник: http://worksbase.ru/matematika/kak-reshat/859-naidite-naimenshee-chislo.html
3. Признаки делимости. Материал из Википедии – свободной энциклопедии. –http://ru.wikipedia.org/wiki/%CF%F0%E8%E7%ED%E0%EA%E8_%E4%E5%EB%E8%EC%EE%F1%F2%E8
Старинная восточная притча:
Давным-давно жил-был старик, который, умирая, оставил своим трем сыновьям 19 верблюдов. Он завещал старшему сыну половину, среднему – четвертую часть, а младшему – пятую. Не сумев найти решения самостоятельно (ведь задача в «целых верблюдах» решения не имеет), братья обратились к мудрецу.
- О, мудрец!- сказал старший брат. - Отец оставил нам 19 верблюдов и велел разделить между собой: старшему – половину, среднему – четверть, младшему – пятую часть. Но 19 не делится ни на 2, ни на 4, ни на 5. Можешь ли ты, о, достопочтенный, помочь нашему горю, ибо мы хотим выполнить волю отца?
- Нет ничего проще, - ответил им мудрец. – Возьмите моего верблюда и идите домой.
Братья дома легко разделили 20 верблюдов пополам, на 4 и на 5.Старший брат получил 10, средний – 5, а младший – 4 верблюда. При этом один верблюд остался (10+5+4=19). Раздосадованные, братья вернулись к мудрецу и пожаловались:
- О, мудрец, опять мы не выполнили волю отца! Вот этот верблюд – лишний.
- Это не лишний, - сказал мудрец,- это мой верблюд. Верните его и идите домой.
Желаем вам успехов в изучении темы
«Делимость чисел. Признаки делимости»!
7