

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока


ИНСТРУКЦИЯ К ЛАБОРАТОРНОЙ РАБОТЕ ПО ВЫСШЕЙ ФИЗИКЕ № 7 Вычисление магнитных полей в магнетиках.
Инструкция к выполнению лабораторной работы по физике
Просмотр содержимого документа
«ИНСТРУКЦИЯ К ЛАБОРАТОРНОЙ РАБОТЕ ПО ВЫСШЕЙ ФИЗИКЕ № 7 Вычисление магнитных полей в магнетиках.»
Цель работы: 1) определить по результатам измерения
п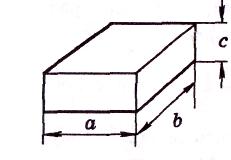 лотность, материала из которого изготовлен прямоугольный брусок (рис. 1.);
лотность, материала из которого изготовлен прямоугольный брусок (рис. 1.);
2) научиться пользоваться штангенциркулем.


 (3)
(3)
Vnp = Апр Впр Спр , (2)

Примечания: 1. Формула (3), взятая в рамку, называется расчетной. расчетная формула приводится всегда к такому виду, чтобы левая ее часть содержала только искомую величину, а правая — только величины, измеряемые прямым способом, и постоянные.
Величина ρ вычисляется по формуле (3).
Обычно индекс *пр» у измеренных значений величин mnp, Aпр, Bпр, Спр опускают (но подразумевают), что мы и будем делать в дальнейшем.
| m | A | B | C |
|
|
|
|
|
|
|
| | △А
|
|
| | | | | | | | | | | | | | | |
ОБРАЗЕЦ:
 = (8,0 ± 0,3) • 103 кг/м3,
= (8,0 ± 0,3) • 103 кг/м3,  = 4 %.
= 4 %.
Вывод: брусок изготовлен из стали, поскольку полученный результат совпадает с табличным значением плотности стали
КОНТРОЛЬНЫЕ ВОПРОСЫ.
Как определить погрешность прибора?
Что такое систематические погрешности?
Что такое случайные погрешности?
Что такое абсолютная и относительная погрешность?
Практическая работа № 2
Тема. Скатывание тел с наклонной плоскости. Определение ускорения, момента инерции и силы трения сцепления разных тел с деревянной наклонной плоскостью.
Цель. Научиться определять ускорение, момент инерции и силу трения сцепления различных тел с деревянной наклонной плоскости.
Оборудование. Наклонная плоскость (из березы, сосны, дуба, ели), рычажные весы, секундомер, линейка, транспортир, сантиметровая лента, сплошной металлический цилиндр, полый цилиндр без торцов, сплошной шар, полый шар.
Теоретические сведения
Пусть тело радиуса R и массой m скатывается с наклонной плоскости, образующей угол α с горизонтом (рис. 1). На тело действуют три силы: сила тяжести P = mg, сила нормального давления плоскости на тело N и сила трения цилиндра о плоскость Fтр., лежащая в этой плоскости. Тело участвует одновременно в двух видах движения: поступательном движении центра масс O и вращательном движении относительно оси, 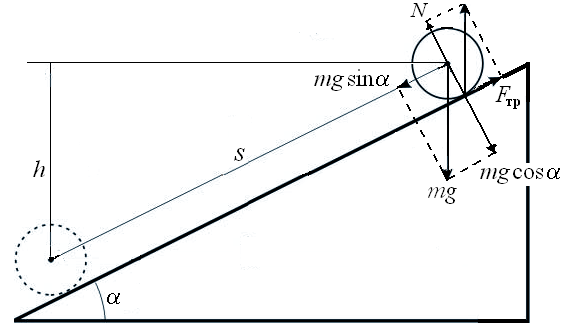 проходящей через центр масс. Так как тело во время движения остается на плоскости, то ускорение центра масс в направлении нормали к наклонной плоскости равно нулю, следовательно
проходящей через центр масс. Так как тело во время движения остается на плоскости, то ускорение центра масс в направлении нормали к наклонной плоскости равно нулю, следовательно
P∙cosα − N = 0. (1)
Уравнение динамики поступательного движения вдоль наклонной плоскости определяется силой трения Fтр. и составляющей силы тяжести вдоль наклонной плоскости mg∙sinα: ma = mg∙sinα − Fтр., (2)
где a – ускорение центра тяжести тела вдоль наклонной плоскости.
Уравнение динамики вращательного движения относительно оси, проходящей через центр масс имеет вид Iε = Fтр.R, (3)
где I – момент инерции, ε – угловое ускорение. Момент силы тяжести и ![]() относительно этой оси равен нулю.
относительно этой оси равен нулю.
Уравнения (2) и (3) справедливы всегда, вне зависимости от того, движется тело по плоскости со скольжением или без скольжения. Но из этих уравнений нельзя определить три неизвестные величины: Fтр., a , необходимо еще одно дополнительное условие.
Если сила трения имеет достаточную величину, то качение тела по наклонной происходит без скольжения. Тогда точки на окружности тела должны проходить ту же длину пути, что и центр масс. В этом случае линейное ускорение a и угловое ускорение ε связаны соотношением a = Rε. (4)
Из уравнения (4) ε = a/R. После подстановки в (3) получаем![]() (5)
(5)
Заменив в (2) Fтр. на (5), получаем![]()
Из последнего соотношения определяем линейное ускорение
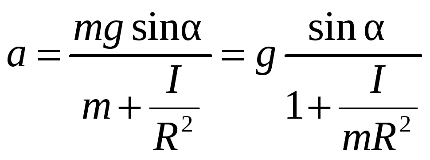 (6)
(6)
Из уравнений (5) и (6) можно вычислить силу трения:
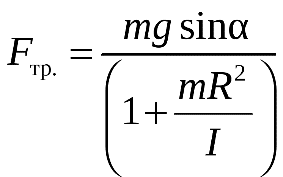 (7)
(7)
Сила трения зависит от угла наклона α, силы тяжести P = mg и от отношения I/mR2. Без силы трения качения не будет. При качении без скольжения играет роль сила трения покоя. Сила трения при качении, как и сила трения покоя, имеет максимальное значение, равное μN. Тогда условия для качения без скольжения будут выполняться в том случае, если Fтр. ≤ μN. (9)
В общем случае момент инерции однородных симметричных тел вращения относительно оси, проходящей через центр масс, можно записать как
I = kmR2, (12)
где k = 0,5 для сплошного цилиндра (диска); k = 1 для полого тонкостенного цилиндра (обруча); k = 0,4 для сплошного шара, k = 0,66 для полого шара
Где s – путь, пройденный центром масс.
Движение по наклонной плоскости является равноускоренным:
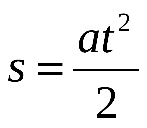
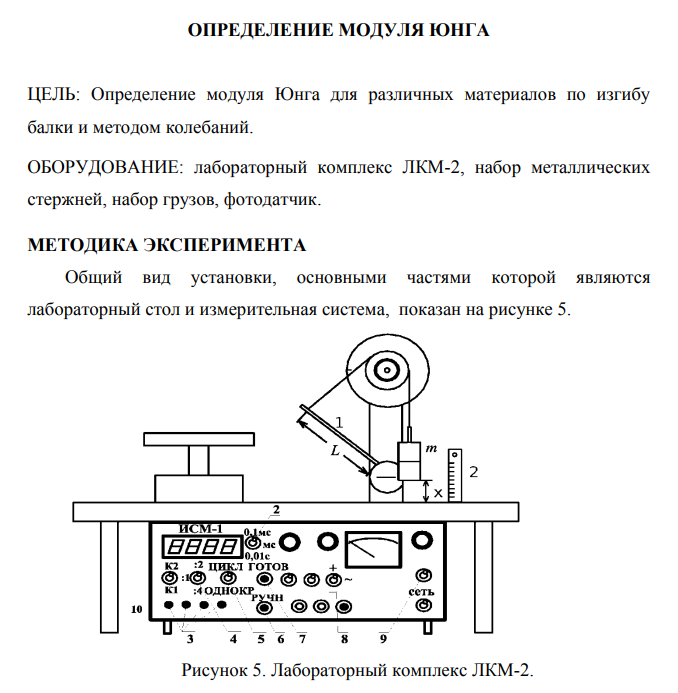
Описание установки и метода измерений
Исследовать качение разных тел по наклонной плоскости можно с помощью наклонной плоскости и электронного секундомера, установка представляет собой наклонную плоскость 1, которую устанавливаем под разными углами α к горизонту. Угол α измеряется с помощью транспортира. На плоскость помещаем различные тела массой m. Время скатывания измеряем секундомером. Пройденное телами расстояние измеряем линейкой , закрепленной вдоль плоскости.
Порядок выполнения работы
1. Установите плоскость под некоторым углом α к горизонту. Поместите тело на наклонную плоскость.
2. Нажмите кнопку «Пуск» секундомера. Измерьте время скатывания.
3. Найдите ускорение тел, массу их на рычажных весах, радиус инерции, момент инерции и силу трения.
4. Ответьте на контрольные вопросы.
5. Сделайте выводы.
Таблица 1
| Название тела | Длина плоскости,м S | Время скатывания с t | Ускорение тела, м\с2 a | Масса тела, кг m | Радиус инерции, м ρ | Радиус тела,м r | Момент инерции, кг*м2 I | Угол наклона плоскости, град α | Сила трения сцепления, Н F |
| Сплошной цилиндр |
|
|
|
|
|
|
|
|
|
| Полый цилиндр |
|
|
|
|
|
|
|
|
|
| Сплошной шар |
|
|
|
|
|
|
|
|
|
| Полый шар |
|
|
|
|
|
|
|
|
|
Под таблицей выполняем вычисления для каждого тела
 вычислите ускорение тела
вычислите ускорение тела
ρ = r – полый цилиндр, ρ =  – сплошной цилиндр ( ρ - радиус инерции)
– сплошной цилиндр ( ρ - радиус инерции)
ρ =  – полый шар, ρ =
– полый шар, ρ =  r - сплошной шар
r - сплошной шар
Ic = ρ2m вычислите момент инерции тела
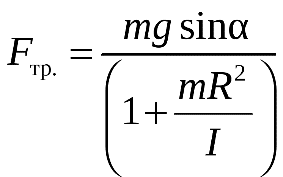 вычислите силу трения качения
вычислите силу трения качения
Сделайте выводы.
Контрольные вопросы
Что называется твердым телом?
Какое движение называют мгновенным вращением?
Сформулируйте теорему Эйлера- Даламбера.
Запишите и сформулируйте условия равновесия твердого тела.




Таким образом модуль Юнга имеет физический смысл коэффициента пропорциональности между механическим напряжением и относительной деформацией. E = 64KL3 \ 3πd4 ; К = (m2 – m1)g \ △ Х
Таблица
| № пп и название | Образец 1 | Образец 2 | Образец 3 |
| Материал | Алюминий | Сталь | Медь |
| Диаметр сечения проволоки, м | 0.002 | 0.002 | 0.002 |
| Длина проволоки, м | 0.2 | 0.2 | 0.2 |
| Масса груза 1, кг | 0.1 | 0.1 | 0.1 |
| Масса груза 2, кг | 0.2 | 0.2 | 0.2 |
| Разность между положением груза х1 и х2, (х2 – х1) | 0.0095 | 0.0175 | 0.4942 |
| К, коэффициент жесткости проволоки, Н\м |
|
|
|
| Е, Модуль Юнга, Н\м2 |
|
|
|
И посчитайте коэффициент жесткости, внутреннее напряжение и модуль Юнга.


Практическая работа № 4
Определение скорости звука в случае продольных и поперечных волн по критическим углам полного отражения
Цель работы: определить скорость звука продольных волн в твердом теле по времени распространения; найти скорости продольной и поперечной звуковых волн с помощью наклонной плоскопараллельной пластины; определить упругие константы алюминия и полиакрила.
Оборудование: ультразвуковой эхоскоп, измерительные датчики-преобразователи, комплект оборудования для исследования продольных и поперечных волн, компьютер.

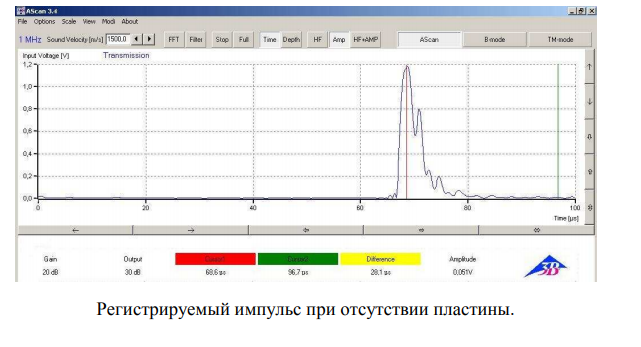
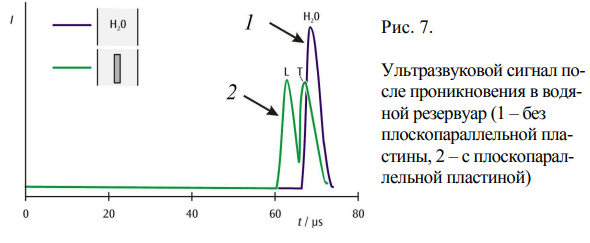 Имеется резервуар с водой. Акустический излучатель крепится к одной его грани, приемник акустического сигнала – к другой. Схема позволяет измерять время прохождения сигнала между излучателем и приемником. Если на пути волны в резервуар поместить пластину из твердого материала (в работе это алюминий и полиакрил), то время прохождение волны через резервуар уменьшится на ∆t , поскольку скорость звука в твердом теле больше, чем в жидкости. Причем, появится два сигнала – от продольной и поперечных волн в пластине (рис. 6).
Имеется резервуар с водой. Акустический излучатель крепится к одной его грани, приемник акустического сигнала – к другой. Схема позволяет измерять время прохождения сигнала между излучателем и приемником. Если на пути волны в резервуар поместить пластину из твердого материала (в работе это алюминий и полиакрил), то время прохождение волны через резервуар уменьшится на ∆t , поскольку скорость звука в твердом теле больше, чем в жидкости. Причем, появится два сигнала – от продольной и поперечных волн в пластине (рис. 6).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ •
Установить переключатель режима в положение TRANS (попер.).
Нанести на передние поверхности ультразвуковых датчиков преобразователей толстый слой связующего геля и плотно прижать ультразвуковые преобразователи к двум длинным сторонам резервуара.
Заполнить резервуар водой.
На ультразвуковом эхоскопе установить регуляторы OUTPUT dB (выходной сигнал, дБ) и GAIN dB (коэффициент усиления, дБ), а также THRESHOLD (порог), WIDE (ширина) и SLOPE (наклон) в такие положения, чтобы получить максимальный уровень звукового сигнала, однако без перегрузки.
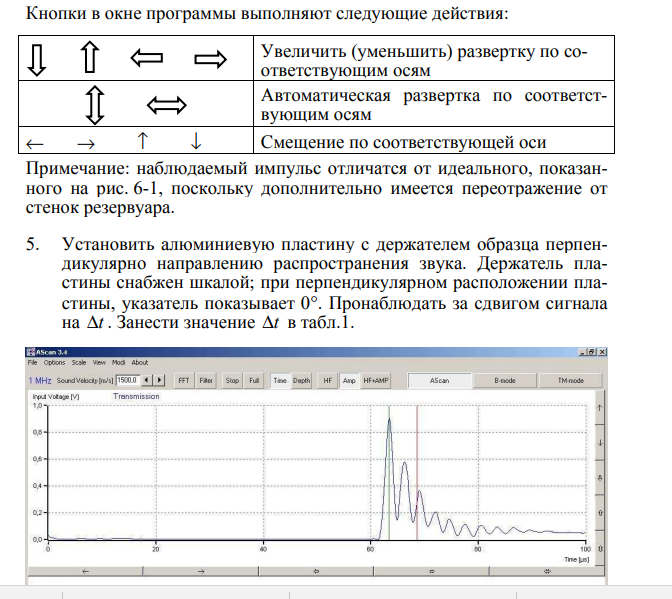
 В окне программы эхоскопа при помощи курсора отметить момент начала регистрации импульса приемником. (В программе имеется два курсора – красный и зеленый, их положение на временной шкале показывается в микросекундах под указателями Cursor 1 и Cursor 2; также показывается разница во времени между курсорами – Difference).
В окне программы эхоскопа при помощи курсора отметить момент начала регистрации импульса приемником. (В программе имеется два курсора – красный и зеленый, их положение на временной шкале показывается в микросекундах под указателями Cursor 1 и Cursor 2; также показывается разница во времени между курсорами – Difference).
Примечание: наблюдаемый импульс отличатся от идеального, показанного на рис. 6-2. 1) Генерируемый эхоскопом импульс имеет длительность ~ 5 мкс. Поэтому, если поперечная волна отстанет от продольной меньше, чем на это время, они будут неразличимы. Их суперпозицией является левый импульс на рисунке. 2) Остальные, затухающие импульсы, являются отражениями волн от границ пластины.
Повернуть алюминиевую пластину и определить угол поворота L α кр , при котором наблюдается исчезновение сигнала продольной волны. Левая часть импульса будет уменьшаться, а правая увеличиваться, поскольку начнет проявляться поперечная волна.
Продолжать поворачивать алюминиевую пластину и определить угол поворота T α кр , при котором наблюдается исчезновение сигнала поперечной волны.
Проделать пункты 6-7 три раза.
Заменить алюминиевую пластину полиакриловой пластиной с держателем образца, которую установить перпендикулярно направлению распространения звука. Определить ∆t
Учитывая примечание п.5., повернуть полиакриловую пластину и определить угол поворота L α кр , при котором наблюдается исчезновение сигнала продольной волны (слева).
Продолжать поворачивать полиакриловую пластину и определить угол поворота T α кр , при котором наблюдается исчезновение сигнала поперечной волны (справа).
Проделать пункты 10-11 три раза.
Результаты измерений занести в таблицу 1.
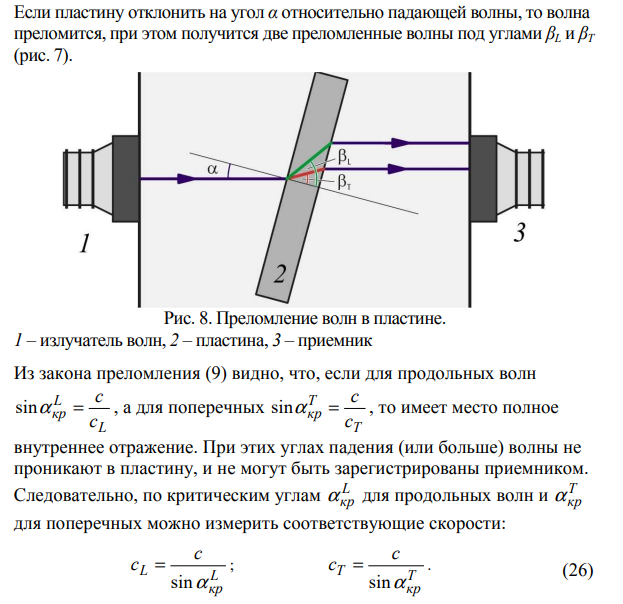
Воспользовавшись данными Приложения, рассчитать скорости распространения продольных и поперечных звуковых волн в полиакриле и алюминии по критическим углам полного отражения по уравнениям (26) и по сдвигу сигнала (27). Результаты занести в таблицу 1 и сравнить их.
Воспользовавшись данными Приложения плотности веществ, рассчитать постоянные упругости, по уравнениям 23-25. Результаты занести в таблицу 2.
|
|
| С L1, м/с | αL | Sinα L | СL м/с | αT | Sinα T | СT, м/с |
| Полистирол | 6*10-5 |
| 8,63 |
|
| 17,45 |
|
|
| Алюминий | 9*10-5 |
| 2,86 |
|
| 5,74 |
|
|
Таблица1
Таблица2
|
| С 1L, м/с | С L, м/с | С T, м/с | ⴜ | G, MПа | E, MПa |
| Полистирол |
|
|
| 0,35 |
|
|
| Алюминий |
|
|
| 0,34 |
|
|
 КОНТРОЛЬНЫЕ ВОПРОСЫ
КОНТРОЛЬНЫЕ ВОПРОСЫ
Запишите уравнение плоской волны.
В чем отличие продольных волн от поперечных?
В чем суть метода определение скорости звука по критическим углам? Каков физический смысл модуля упругости, модуля сдвига и коэффициента Пуассона?










ЛАБОРАТОРНОЙ РАБОТЫ ПО ВЫСШЕЙ ФИЗИКЕ № 6
ТЕМА. Вычисление электрических полей
с помощью теоремы Гаусса.
ЦЕЛЬ. Научиться вычислять различные электрические поляс помощью теоремы Гаусса.
ОБОРУДОВАНИЕ. Наэлектризованный шарик,
металлическая пластинка,
цилиндр, калькулятор, компьютер.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Теорема Гаусса позволяет в ряде случаев найти напряженность поля простыми средствами. Продемонстрируем возможности теоремы Гаусса на нескольких полезных для дальнейшего примерах. Прежде чем приступить к рассмотрению этих примеров, введем понятия поверхностной и линейной плотностей заряда.
Если заряд сосредоточен в тонком поверхностном слое несущего заряд тела, распределение заряда в пространстве можно охарактеризовать с помощью поверхностной плотности , которая определяется выражением
, которая определяется выражением

Здесь dq — заряд, заключенный в слое площади dS. Под dS подразумевается физически бесконечно малый участок поверхности. Если заряд распределен по объему или поверхности цилиндрического тела (равномерно в каждом сечении), используется линейная плотность заряда

(dl —длина физически бесконечно малого отрезка цилиндра, dq — заряд, сосредоточенный на этом отрезке).
Поле бесконечной однородно заряженной плоскости.
П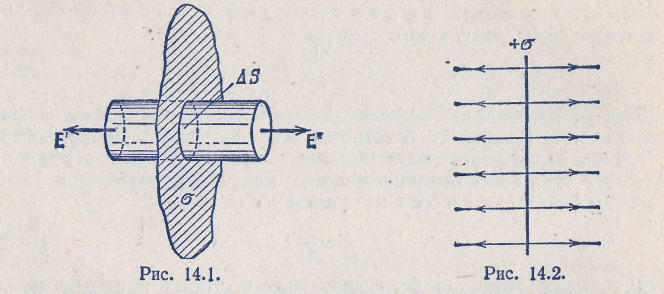 усть поверхностная плотность заряда во всех точках плоскости одинакова и равна
усть поверхностная плотность заряда во всех точках плоскости одинакова и равна  ; для определенности будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность поля в любой точке имеет направление, перпендикулярное к плоскости. Действительно, поскольку плоскость бесконечна и заряжена однородно, нет никаких оснований к тому, чтобы вектор Е отклонялся в какую-либо сторону от нормали к плоскости. Далее очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна по направлению.
; для определенности будем считать заряд положительным. Из соображений симметрии вытекает, что напряженность поля в любой точке имеет направление, перпендикулярное к плоскости. Действительно, поскольку плоскость бесконечна и заряжена однородно, нет никаких оснований к тому, чтобы вектор Е отклонялся в какую-либо сторону от нормали к плоскости. Далее очевидно, что в симметричных относительно плоскости точках напряженность поля одинакова по величине и противоположна по направлению.
Представим себе мысленно цилиндрическую поверхность с образующими, перпендикулярными к плоскости, и  основаниями величины
основаниями величины  S, расположенными относительно плоскости симметрично (рис. 14.1). В силу симметрии Е'=Е"=Е. Применим к поверхности теорему Гаусса. Поток через боковую часть поверхности будет отсутствовать, поскольку Еп в каждой ее точке равна нулю. Для оснований Еп совпадает с Е. Следовательно, суммарный поток через поверхность равен 2Е
S, расположенными относительно плоскости симметрично (рис. 14.1). В силу симметрии Е'=Е"=Е. Применим к поверхности теорему Гаусса. Поток через боковую часть поверхности будет отсутствовать, поскольку Еп в каждой ее точке равна нулю. Для оснований Еп совпадает с Е. Следовательно, суммарный поток через поверхность равен 2Е S. Внутри поверхности заключен заряд о
S. Внутри поверхности заключен заряд о S. Согласно теореме Гаусса должно выполняться условие
S. Согласно теореме Гаусса должно выполняться условие
2E S=
S= , из которого
, из которого
E=
Полученный нами результат не зависит от длины цилиндра. Это означает, что на любых расстояниях от плоскости напряженность поля одинакова по величине. Вид линий напряженности показан на рис. 14.2. Для отрицательно заряженной плоскости результат будет таким же, лишь направление вектора Е и линий напряженности изменится на обратное.
Е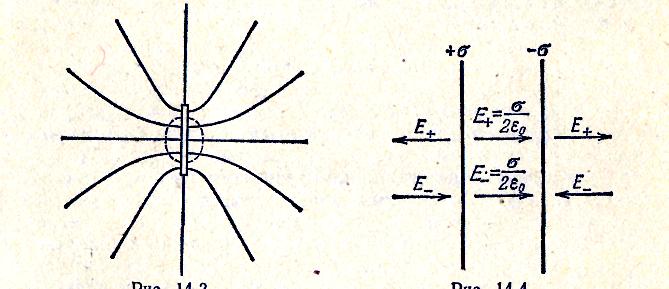 сли взять плоскость конечных размеров, например заряженную тонкую пластинку 1), то полученный выше результат будет справедливым только для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки (на рис. 14.3область этих точек обведена пунктирной кривой). По мере удаления от плоскости или приближения к ее краям поле будет все больше отличаться от поля бесконечной заряженной плоскости. Характер поля на больших расстояниях легко представить, если учесть, что на расстояниях, значительно превышающих размеры пластинки, создаваемое, ею, поле можно рассматривать как поле точечного заряда.
сли взять плоскость конечных размеров, например заряженную тонкую пластинку 1), то полученный выше результат будет справедливым только для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки (на рис. 14.3область этих точек обведена пунктирной кривой). По мере удаления от плоскости или приближения к ее краям поле будет все больше отличаться от поля бесконечной заряженной плоскости. Характер поля на больших расстояниях легко представить, если учесть, что на расстояниях, значительно превышающих размеры пластинки, создаваемое, ею, поле можно рассматривать как поле точечного заряда.
Поле двух разноименно заряженных плоскостей.
Поле двух параллельных бесконечных плоскостей, заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью а, можно найти как суперпозицию полей, создаваемых каждой из плоскостей в отдельности (рис. 14.4). В области между плоскостями складываемые поля имеют одинаковое направление, так что результирующая напряженность равна
E= (14.4)
(14.4)
Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю.
Таким образом, поле оказывается сосредоточенным между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению; следовательно, поле однородно. Линии напряженности представляют собой совокупность параллельных , равноотстоящих прямых. Полученный нами результат приближенно справедлив и для плоскостей конечных размеров, если расстояние между плоскостями много меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности наблюдаются только вблизи краев пластин (рис. 14.5).
П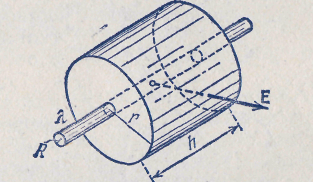 оле бесконечного заряженного цилиндра.
оле бесконечного заряженного цилиндра.
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью.
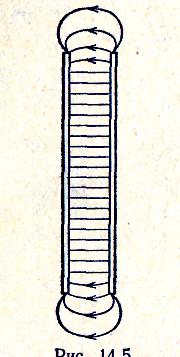 Из соображений симметрии следует, что напряженность поля в любой точке должна быть направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а величина напряженности может зависеть только от расстояния r от оси цилиндра. Представим себе мысленно коаксиальную с заряженной поверхностью замкнутую цилиндрическую поверхность радиуса г и высоты h (рис. 14.6). Для оснований цилиндра En=0, для боковой поверхности Еп =Е(r) (заряд предполагаем положительным). Следовательно, поток вектора Е через рассматриваемую поверхность равен E(r)-2nrh. Если гR, внутрь поверхности попадает заряд q=
Из соображений симметрии следует, что напряженность поля в любой точке должна быть направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а величина напряженности может зависеть только от расстояния r от оси цилиндра. Представим себе мысленно коаксиальную с заряженной поверхностью замкнутую цилиндрическую поверхность радиуса г и высоты h (рис. 14.6). Для оснований цилиндра En=0, для боковой поверхности Еп =Е(r) (заряд предполагаем положительным). Следовательно, поток вектора Е через рассматриваемую поверхность равен E(r)-2nrh. Если гR, внутрь поверхности попадает заряд q= h (
h ( — линейная плотность заряда). Применив теорему Гаусса, получим
— линейная плотность заряда). Применив теорему Гаусса, получим
E(r)2 rh=
rh= , отсюдаE ( r )=
, отсюдаE ( r )=
Если rR, рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего Е(r)=0.
Таким образом, внутри равномерно заряженной цилиндрической поверхности бесконечной длины поле отсутствует. Напряженность поля вне поверхности определяется линейной плотностью заряда  и расстоянием r от оси цилиндра.
и расстоянием r от оси цилиндра.
П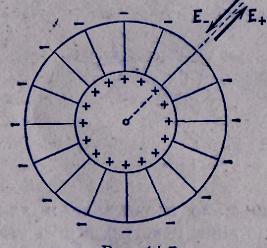 оле отрицательно заряженного цилиндра отличается от поля цилиндра, заряженного положительно, только направлением вектора Е.
оле отрицательно заряженного цилиндра отличается от поля цилиндра, заряженного положительно, только направлением вектора Е.
Из формулы (14.5) следует, что, уменьшая радиус цилиндра R (при неизменной линейной плотности заряда 1), можно получить вблизи поверхности цилиндра поле с очень большой напряженностью.
Подставив в (14.5)  = 2
= 2 R
R и положив r=R, получим для напряженности поля в непосредственной близости к поверхности цилиндра значение.
и положив r=R, получим для напряженности поля в непосредственной близости к поверхности цилиндра значение.
E( R )=
С помощью принципа суперпозиции легко найти поле двух коаксиальных цилиндрических поверхностей, заряженных с одинаковой по величине,
но отличающейся знаком линейной плотностью  (рис. 14.7). Внутри меньшего и вне большего цилиндров
(рис. 14.7). Внутри меньшего и вне большего цилиндров
ми много меньше их длины (цилиндрический конденсатор). Заметные отступления от поля поверхностей бесконечной длины будут наблюдаться только вблизи краев цилиндров.
Поле заряженной сферической поверхности.
Поле, создаваемое сферической поверхностью радиуса R, заряженной с постоянной поверхностной плотностью  будет, очевидно, центрально-симметричным. Это означает, что направление вектора Е в любой точке проходит через центр сферы, а величина напряженности является функцией расстояния r от центра сферы. Вообразим концентрическую с заряженной сферой поверхность радиуса г. Для всех точек этой поверхности Еn=Е(r). Если rR, внутрь поверхности попадает весь заряд q, распределенный по сфере. Следовательно,
будет, очевидно, центрально-симметричным. Это означает, что направление вектора Е в любой точке проходит через центр сферы, а величина напряженности является функцией расстояния r от центра сферы. Вообразим концентрическую с заряженной сферой поверхность радиуса г. Для всех точек этой поверхности Еn=Е(r). Если rR, внутрь поверхности попадает весь заряд q, распределенный по сфере. Следовательно,
E( r )4 r2=
r2=
E( r )= ( r
( r R)
R)
откуда
Сферическая поверхность радиуса г, меньшего, чем R, не будет содержать зарядов, вследствие чего для rR получается E(г)=0.
Таким образом, внутри сферической поверхности, заряженной с постоянной поверхностной плотностью  , поле отсутствует. Вне этой поверхности поле тождественно с полем точечного заряда той же величины, помещенного в центр сферы.
, поле отсутствует. Вне этой поверхности поле тождественно с полем точечного заряда той же величины, помещенного в центр сферы.
Используя принцип суперпозиции, легко показать, что поле двух концентрических сферических поверхностей (сферический конденсатор), несущих одинаковые по величине и противоположные по знаку заряды +q и —q, сосредоточено в зазоре между поверхностями, причем величина напряженности поля в этом зазоре определяется формулой (14.7).
Поле объемно - заряженного шара.
Пусть шар радиуса R заряжен с постоянной объемной плотностью  . Поле в этом случае обладает центральной симметрией. Легко сообразить, что для поля вне шара получается тот же результат (см. формулу (14.7)), что и в случае поверхностно -заряженной сферы. Однако для точек внутри шара результат будет иным. Сферическая поверхность радиуса r (rR) заключает в себе заряд, равный
. Поле в этом случае обладает центральной симметрией. Легко сообразить, что для поля вне шара получается тот же результат (см. формулу (14.7)), что и в случае поверхностно -заряженной сферы. Однако для точек внутри шара результат будет иным. Сферическая поверхность радиуса r (rR) заключает в себе заряд, равный -4/3
-4/3 г3.
г3.
Поэтому теорема Гаусса для такой поверхности запишется следующим образом:
.
E( r)4 Отсюда, заменив
Отсюда, заменив  через q/(4/3
через q/(4/3 R3
R3 ), получаем
), получаем
E( r )=  Таким образом, внутри шара напряженность поля растет линейно с расстоянием r от центра шара. Вне шара напряженность убывает по такому же закону, как и у поля точечного заряда.
Таким образом, внутри шара напряженность поля растет линейно с расстоянием r от центра шара. Вне шара напряженность убывает по такому же закону, как и у поля точечного заряда.
С помощью штангенциркуля и линейки измерьте диаметр шара, линейные размеры пластины, расстояние между пластинами, длину цилиндра и радиус его сечения.
Запишите данные в таблицу.
Сделайте вычисление напряженности полей шара, плоскостей и цилиндра и также занесите в таблицу.
Сделайте вывод и ответьте на контрольные вопросы.
| | Q, Кл | | | L, м | S, м2 | R, м | D, м | | E, В/м |
| Пластина | | | | | | | | | |
| Две пластины | | | | | | | | | |
| Цилиндр | | | | | | | | | |
| Поверхность сферы | | | | | | | | | |
| Объемно заряж. шар. | | | | | | | | | |
Что называется поверхностной плотностью заряда?
Какое ограничение накладывается на поле пластинки конечных размеров?
Что представляет собой поле между двумя пластинами, и где наблюдаются отклонения от однородности?
Чем отличается поле отрицательно заряженного цилиндра от поля положительно заряженного цилиндра?
Вычисление электрических полей в диэлектриках.
ЦЕЛЬ. Научиться вычислять различные электрические поля в диэлектриках.
ОБОРУДОВАНИЕ. Пластина из диэлектрика, сфера из однородного изотропного диэлектрика.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
П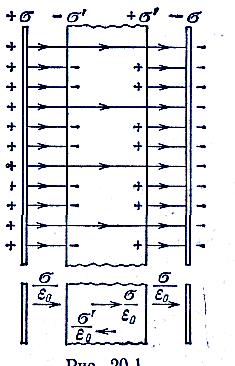 оле внутри плоской пластины. Рассмотрим две бесконечные параллельные разноименно заряженные плоскости. Пусть создаваемое ими в вакууме поле характеризуется напряженностью Е0
оле внутри плоской пластины. Рассмотрим две бесконечные параллельные разноименно заряженные плоскости. Пусть создаваемое ими в вакууме поле характеризуется напряженностью Е0
и смещением D0= E0. снесем в это поле пластину из однородного изотропного диэлектрика и расположим ее так, как показано на рис. 20.1. Под действием поля диэлектрик поляризуется, и на его поверхностях появятся связанные заряды плотности
E0. снесем в это поле пластину из однородного изотропного диэлектрика и расположим ее так, как показано на рис. 20.1. Под действием поля диэлектрик поляризуется, и на его поверхностях появятся связанные заряды плотности  '. Эти заряды создадут внутри пластины однородное поле, напряженность которого согласно формуле (14.4) равна Е' =
'. Эти заряды создадут внутри пластины однородное поле, напряженность которого согласно формуле (14.4) равна Е' =
 . Вне диэлектрика в данном случаеE0=0. Напряженность поля Е0 равна
. Вне диэлектрика в данном случаеE0=0. Напряженность поля Е0 равна  /
/ „. Оба поля направлены навстречу друг другу, следовательно, внутри диэлектрика /'
„. Оба поля направлены навстречу друг другу, следовательно, внутри диэлектрика /'
E=E0 - =E0 -
=E0 -  =
= 

Вне диэлектрика Е=Е0.
Поляризация диэлектрика обусловлена полем (20.1). Это поле перпендикулярно к поверхностям пластины. Поэтому Еп=Е и в соответствии с (18.2)  . Подставив это значение в формулу (20.1), получим
. Подставив это значение в формулу (20.1), получим
E=E0 -  E
E
Откуда E= =
=
Итак, в рассматриваемом случае диэлектрическая проницаемость  показывает, во сколько раз ослабляется поле в диэлектрике.
показывает, во сколько раз ослабляется поле в диэлектрике.
Умножив (20.2) на  , получим электрическое смещение внутри пластины
, получим электрическое смещение внутри пластины
D= =
= =D0 (20.3)
=D0 (20.3)
Таким образом, электрическое смещение внутри пластины совпадает с электрическим смещением внешнего поля.
D0, Заменив в (20.3) EQ через  получим, что D=
получим, что D= .Чтобы найти
.Чтобы найти  ', выразим в (20.2) Е и Е0 через плотности зарядов
', выразим в (20.2) Е и Е0 через плотности зарядов  =
= Отсюда
Отсюда
 (20.5)
(20.5)
Рис. 20.1 выполнен в предположении, что в соответствии с этим густота линий Е в диэлектрике в три раза меньше, чем вне пластины. Линии проведены на одинаковых расстояниях друг от друга, поскольку поле однородно. В данном случае можно найти, не прибегая к формуле (20.5). Действительно, раз напряженность поля внутри пластины в три раза меньше, чем вне ее, то из трех линий напряженности, начинающихся (или заканчивающихся) на сторонних зарядах, две должны заканчиваться (соответственно начинаться) на связанных зарядах. Отсюда вытекает, что плотность связанных зарядов должна быть равна 2/3 плотности сторонних зарядов.
В гауссовой системе напряженность Е', создаваемая связанными зарядами  , равна 4
, равна 4 '.
'.
Поверхностная плотность а' связана с напряженностью Е соотношением о'= =кЕп. Следовательно, можно написать, что
Е = Ео—4пкЕ. Отсюда
E=
м образом, диэлектрическая проницаемость е, так же как и е в СИ, показывает, во сколько раз ослабляется поле внутри диэлектрика. Следовательно, значения е в СИ и в гауссовой системе совпадают. Отсюда, приняв во внимание (19.5) и (19.13), заключаем, что диэлектрическая восприимчивость в гауссовой системе (*гс) и в СИ (иси) отличаются друг от друга множителем 4л:
хси=4лхгс. (20.6)
П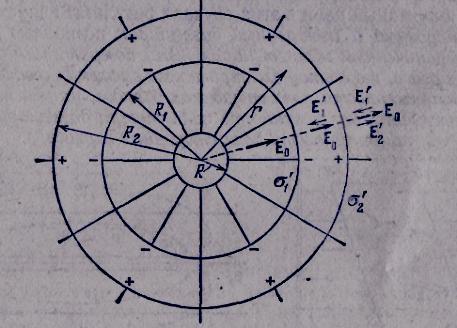 оле внутри шарового слоя. Окружим заряженную сферу радиуса R концентрическим шаровым слоем из однородного изотропного диэлектрика (рис. 20.2). На внутренней поверхности слоя появится связанный заряд q1, распределенный с плотностью
оле внутри шарового слоя. Окружим заряженную сферу радиуса R концентрическим шаровым слоем из однородного изотропного диэлектрика (рис. 20.2). На внутренней поверхности слоя появится связанный заряд q1, распределенный с плотностью  1, на наружной — заряд q2, распределенный с плотностью
1, на наружной — заряд q2, распределенный с плотностью  2 . Знак заряда q'2 совпадает со знаком заряда q сферы, знак q( ему противоположен. Заряды q1 и q'2 создают на расстоянии г, превышающем соответственно r! и R2, поле, совпадающее с полем точечного заряда такой же величины (см. формулу (14.7)). Внутри поверхностей, по которым они распределены, заряды q\ и q'z поля не создают. Следовательно, напряженность поля Е' внутри диэлектрика равна
2 . Знак заряда q'2 совпадает со знаком заряда q сферы, знак q( ему противоположен. Заряды q1 и q'2 создают на расстоянии г, превышающем соответственно r! и R2, поле, совпадающее с полем точечного заряда такой же величины (см. формулу (14.7)). Внутри поверхностей, по которым они распределены, заряды q\ и q'z поля не создают. Следовательно, напряженность поля Е' внутри диэлектрика равна
E=
и противоположна по направлению напряженности поля Е0. Результирующее поле в диэлектрике (20J)
убывает по закону 1/г2. E=E(r)  . Именно эта напряженность определяет величину
. Именно эта напряженность определяет величину  (20.8)
(20.8)  (в каждой точке поверхности \Еп\—Е).
(в каждой точке поверхности \Еп\—Е).
Е(Г)= E0 -  Отсюда находим, что внутри диэлектрика Е=Е/
Отсюда находим, что внутри диэлектрика Е=Е/ и, следовательно, D=
и, следовательно, D= (ср. с формулами (20.2) и (20.3)). Поле внутри диэлектрика изменяется по закону 1/г2. Поэтому имеет место соотношение
(ср. с формулами (20.2) и (20.3)). Поле внутри диэлектрика изменяется по закону 1/г2. Поэтому имеет место соотношение =
=  Отсюда вытекает, что q1/=q'2. Следовательно, поля, создаваемые этими зарядами, на расстояниях, превышающих R2, взаимно уничтожают друг друга, так что вне шарового слоя E'=0 и E=E0
Отсюда вытекает, что q1/=q'2. Следовательно, поля, создаваемые этими зарядами, на расстояниях, превышающих R2, взаимно уничтожают друг друга, так что вне шарового слоя E'=0 и E=E0
Положив R1 равным R, а R2= , придем к случаю заряженной сферы, погруженной в безграничный, однородный и изотропный диэлектрик. Напряженность поля вне такой сферы равна
, придем к случаю заряженной сферы, погруженной в безграничный, однородный и изотропный диэлектрик. Напряженность поля вне такой сферы равна
Е=
 Такова же будет напряженность поля, создаваемого в безграничном диэлектрике точечным зарядом.
Такова же будет напряженность поля, создаваемого в безграничном диэлектрике точечным зарядом.
Оба рассмотренных примера характерны тем, что диэлектрик был однородным и изотропным, а ограничивающие его поверхности совпадали с эквипотенциальными поверхностями поля сторонних зарядов. Полученный нами в этих случаях результат является общим. Если однородный и изотропный диэлектрик полностью заполняет объем, ограниченный эквипотенциальными поверхностями поля сторонних зарядов, то вектор электрического смещения совпадает с вектором напряженности поля сторонних зарядов, умноженным на е„, и, следовательно, напряженность поля внутри диэлектрика в е раз меньше, чем напряженность поля сторонних зарядов.
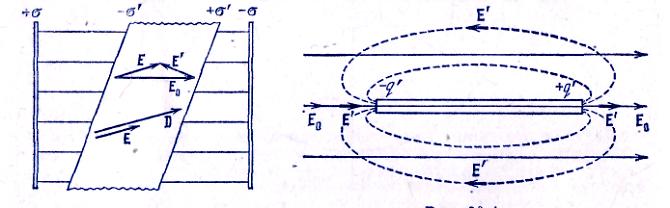
Если упомянутые условия не соблюдаются, векторы D и Е не совпадают. На рис. 20.3 показано поле в пластине диэлектрика, перекошенной относительно плоскостей, несущих сторонние заряды. Вектор Е' перпендикулярен к граням пластины, поэтому Е и Д не коллинеарны. Вектор D направлен так же, как Е, следовательно, D и е Е0 не совпадают по направлению. Можно показать, что они не совпадают и по величине.
В рассмотренных выше примерах из-за специально выбранной формы диэлектрика поле Е' было отлично от нуля только внутри диэлектрика. В общем случае Е' может быть отлично от нуля и за пределами диэлектрика. Поместим в первоначально однородное поле стержень из диэлектрика (рис. 20.4). Вследствие поляризации на концах стержня образуются связанные заряды противоположных знаков. Их поле вне стержня эквивалентно полю диполя (линии Е* показаны на рисунке пунктиром). Легко сообразить, что результирующее поле Е вблизи концов стержня больше поля Е0.
ХОД РАБОТЫВнимательно прочитайте теоретические сведения.
Измерьте линейкой линейные размеры диэлектрических пластин.
Запишите в таблицу.
Найдите радиус диэлектрической сферы и запишите его в таблицу.
Вычислите напряженность поля вне такой сферы.
| | Q, нКл | | А, м | В, м | R, м | E, В/м |
| Поле внутри плоской пластины. | 5 | | | | | |
| Поле внутри шарового слоя. | 10 | | | | | |
КОНТРОЛЬНЫЕ ВОПРОСЫ.
Что называется диэлектриком?
Расскажите о механизме поляризации диэлектриков?
Что показывает диэлектрическая проницаемость?
Какова напряженность поля, создаваемого в безграничном диэлектрике точечным зарядом?
Тема. Правила Кирхгофа. Лабораторная работа №8
Расчет разветвленных цепей по правилам Кирхгофа.
Цель.
Научиться рассчитывать разветвленные цепи по правилам Кирхгофа. Закрепить ранее полученные знания методом решения задач и при выполнении лабораторной работы.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В общем случае на практике часто приходится рассчитывать сложные разветвленные электрические цепи, содержащие узлы.
 Обычно большие трудности вызывают задачи, связанные с нахождением силы токов во всех участках разветвленной цепи, если заданы сопротивления и ЭДС. Непосредственное применение закона Ома затруднительно и приводит к ошибкам в расчете. Трудности при решении подобных задач упрощаются, если применять правила Кирхгофа*.
Обычно большие трудности вызывают задачи, связанные с нахождением силы токов во всех участках разветвленной цепи, если заданы сопротивления и ЭДС. Непосредственное применение закона Ома затруднительно и приводит к ошибкам в расчете. Трудности при решении подобных задач упрощаются, если применять правила Кирхгофа*.
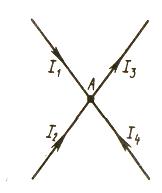
Узлом А в разветвленной цепи называют точку, в которой сходится не меньше трех проводников (рис.)
Алгебраическая сумма токов, сходящихся в узле, равна нулю
(первое правило Кирхгоффа): 
Это правило можно сформулировать и так: количество зарядов, приходящих в данную точку проводника за некоторое время, равно количеству зарядов, уходящих из данной точки за то же время.
Токи, подходящие к узлу, считаются положительными, а отходящие — отрицательными. Например, для узла A (рис.) первое правило запишется так: I1,+I2-I3+I4=0.
Обобщением закона Ома является второе правило Кирхгофа, оно относится к любому замкнутому контуру разветвленной электрической цепи: в любом замкнутом контуре разветвленной цепи алгебраическая сумма ЭДС равна алгебраической сумме произведений токов на сопротивления соответствующих участков этого контура:
 [т — число участков в замкнутом контуре, п — число источников тока].
[т — число участков в замкнутом контуре, п — число источников тока].
При использовании правил Кирхгофа расчет разветвленной цепи постоянного тока следует производить в такой последовательности.
Произвольно выбрать направление обхода контура (по ходу часовой стрелки или против).
Произвольно выбрать и обозначить на схеме стрелками направление токов на всех участках цепи, причем в пределах одного участка (участок —это часть цепи между соседними узлами) ток должен иметь только одно значение и направление.
Произвольно замкнутые контуры выделяются так, чтобы каждый новый контур содержал хотя бы один участок цепи, не входящий в ранее рассмотренные контуры.
Если выбранное направление обхода контура совпадает с направлением тока I то произведение IR, берется со знаком плюс, и наоборот.
Перед E, ставится знак плюс, если при обходе контура приходится идти внутри источника от отрицательного полюса к положительному (т.е. если на пути обхода контура потенциал возрастает), в обратном случае ЭДС записывается со знаком минус.
Правила Кирхгофа позволяют определить силу и направление тока в любой части разветвленной цепи, если известны сопротивления ее участков и включенные в них ЭДС.
Для системы из п проводников, образующих k узлов, составляют п уравнений: (k - 1) уравнений для узлов и п - (k - 1) уравнений для независимых замкнутых контуров.
I2. как на участке от источника  до точки 3.
до точки 3.
Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы э. д. с. и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи. Можно решить и задачи иного рода, например, найти э. д. с., которые нужно включить в каждый из участков цепи, чтобы получить при заданных сопротивлениях нужные токи.
ХОД РАБОТЫ
Составьте цепь по схеме нарисованной на рисунке.
Определите с помощью амперметра и вольтметра напряжение и силу тока.
Пользуясь правилами Кирхгофа, посчитайте ЭДС цепи и докажите, что правила Кирхгофа справедливы.
Результаты измерений и вычислений занесите в таблицу.
Сделайте вывод и ответьте на контрольные вопросы.
| I, А | R, Ом | U, В | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
КОНТРОЛЬНЫЕ ВОПРОСЫ.
Сформулируйте правила Кирхгофа.
Сформулируйте закон Ома для всей цепи.
Чему равно число независимых уравнений составленных по правилам Кирхгофа.
Что нужно помнить, составляя уравнения по второму правилу Кирхгофа.
Цель. Научиться применять закон Фарадея для определения элементарного электрического заряда.
Оборудование. Электролитическая ванна с водным раствором сульфата меди и медными электродами, источник постоянного тока, секундомер, амперметр, весы, реостат, наждачная и фильтровальная бумага, выключатель, сушильная камера, соединительные провода.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
З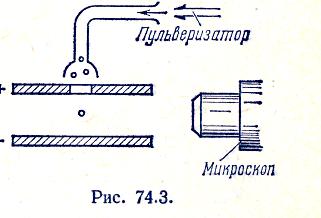 аряд электрона был определен с большой точностью Милликеном в 1909 г. В закрытое пространство между горизонтально рас-
аряд электрона был определен с большой точностью Милликеном в 1909 г. В закрытое пространство между горизонтально рас-
положенными пластинами конденсатора (рис. 74.3) Милликен вводил мельчайшие капельки масла. При разбрызгивании капельки электризовались, и их можно было устанавливать неподвижно, подбирая величину и знак напряжения на конденсаторе. Равновесие наступало при условии
Р'=е'Ездесь е'— заряд капельки, Р'— результирующая силы тяжести и архимедовой силы, равная
Р'=
(р — плотность капельки, т — ее радиус, р„ — плотность воздуха). Из формул (74.9) и (74.10), зная г, можно было найти е. Для определения радиуса измерялась скорость v0 равномерного падения капельки в отсутствие поля. Равномерное движение капельки устанавливается при условии, что сила Р' уравновешивается силой сопротивления F=
 rv.
rv.  — вязкость воздуха): Р' = 6
— вязкость воздуха): Р' = 6 rv0. (74.11)
rv0. (74.11)
Движение капельки наблюдалось с помощью микроскопа. Для измерения определялось время, за которое капелька проходила расстояние между двумя нитями, видимыми в поле зрения микроскопа. Точно зафиксировать равновесие капельки очень трудно. Поэтому вместо поля, отвечающего условию (74.9), включалось такое поле, под действием которого капелька начинала двигаться с небольшой скоростью вверх. Установившаяся скорость подъема vb определяется из условия, что сила Р' и сила 6 r v в сумме уравновешивают силу е'Е: P' + 6
r v в сумме уравновешивают силу е'Е: P' + 6 rvE = e'E. (74.12)
rvE = e'E. (74.12)
Исключив из уравнения (74.10), (74.11) и (74.12) Р' и r, получим выражение для е':


(в эту формулу Милликен вносил поправку, учитывающую, что размеры капелек были сравнимы с длиной свободного пробега молекул воздуха).
Итак, измерив, скорость свободного падения капельки vu и скорость ее подъема ve в известном электрическом поле Е, можно было найти заряд капельки ё'. Произведя измерение скорости vb при некотором значении заряда е', Милликен вызывал ионизацию воздуха, облучая пространство между пластинами рентгеновскими лучами. Отдельные ионы, прилипая к капельке, изменяли ее заряд, в результате чего скорость ve также менялась. После измерения нового значения скорости снова облучалось пространство между пластинами и т. д.
Измеренные Милликеном изменения заряда капельки Ае' и сам заряд е' каждый раз получались целыми кратными одной и той же величины е. Тем самым была экспериментально доказана дискретность электрического заряда, т. е. тот факт, что всякий заряд слагается из элементарных зарядов одинаковой величины. Значение элементарного заряда, установленное с учетом измерений Милликена и данных, полученных другими методами, равно e= 1,60 10-19 Кл . Такую же величину имеет заряд электрона.
Из (74.7) и (74.13) получается для массы покоя электрона значение M= 0.91 10-30 кг приблизительно в 1840 раз меньше массы самого легкого из атомов — атома водорода.
В обнаружении дискретной природы электричества сыграли большую роль законы электролиза, установленные экспериментально Фарадеем в 1836 г. Согласно этим законам масса т вещества, выделяющегося при прохождении тока через электролит, пропорциональна переносимому током заряду q
т= (74.15)
(74.15)
Здесь М — масса моля выделяющегося вещества, n — валентность этого вещества, F — постоянная Фарадея (число Ф а р а д е я), равная
F=96,5-103 Кл/моль. (74.16)
Электролитами называются растворы солей, щелочей или кислот в воде и некоторых других жидкостях, а также расплавы солей, являющихся в твердом состоянии ионными кристаллами. В электролитах при прохождении через них тока происходят химические превращения. Такие вещества называются проводниками второго рода, в отличие от проводников первого рода, у которых прохождение тока не сопровождается химическими превращениями. Разделив обе части равенства (74.15) на массу иона, получим
N=
(Nа — число Авогадро, N — количество ионов, содержащихся в массе т). Отсюда для заряда одного иона получается значение
 =
=
 Следовательно, заряд иона оказывается целым кратным величины e=
Следовательно, заряд иона оказывается целым кратным величины e=  , которая представляет собой элементарный заряд.
, которая представляет собой элементарный заряд.
Таким образом, из анализа законов электролиза вытекает дискретность зарядов, которыми могут обладать ионы в электролитах.
Подстановка в (74.17) значения (74.16) для F и найденного из опытов Перрена значения N& дает для е величину, хорошо согласующуюся со значением, найденным Милликеном.
намного превосходят точность опытов Перрена по определению NA, соотношение (74.17) было использовано для определения числа Авогадро. При этом было взято значение F, найденное из опытов по электролизу, и значение е, полученное Милликеном.
ХОД РАБОТЫ В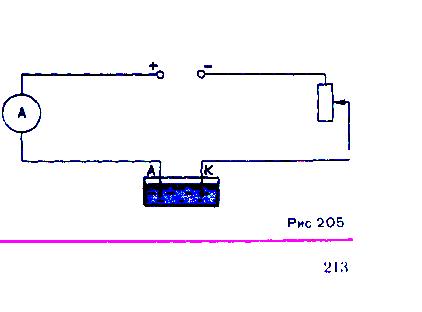 звесьте катод, заранее сделав на его верхней части отметку, чтобы в дальнейшем не перепутать его с анодом.
звесьте катод, заранее сделав на его верхней части отметку, чтобы в дальнейшем не перепутать его с анодом.
Укрепите электроды в держателе и, не опуская электроды в ванну с
раствором, составьте электрическую цепь. Проверьте надежность
электрических контактов, правильность присоединения электродов к
источнику тока, правильность включения амперметра.
Опустите электроды в ванну с раствором, замкните цепь, установите с
помощью реостата силу тока в цепи не больше 1А. Процесс электролиза должен длиться 15-20 мин, при этом силу тока в цепи поддерживайте неизменной.
После завершения опыта разомкните цепь, вытяните медный катод, осторожно промойте его проточной водой, высушите и взвесьте.
Вычислите значение заряда электрона, максимальные абсолютные и относительные погрешности измерения силы тока и времени, определите абсолютную погрешность измерения массы, вычислите максимальные погрешности измерения значения заряда электрона.
 ,
,
где М- молярная масса, n- валентность.
Запишите результат определения заряда электрона. Сравните опытное значение заряда электрона с табличным.

 ,
, 
КОНТРОЛЬНЫЕ ВОПРОСЫ.
Какую из величин в данной работе следует измерять с наибольшей точностью, чтобы получить более точное значение заряда электрона?
Сформулируйте законы электролиза.
В чем заключался опыт Милликена?
Инструкция к лабораторной работе №10
РАСЧЕТ КОНТУРА С ТОКОМ В МАГНИТНОМ ПОЛЕ. ИЗУЧЕНИЕ РАБОТЫ АСИНХРОННОГО ДВИГАТЕЛЯ.
Цель. Изучить работу асинхронного двигателя.
Оборудование. Набор по трехфазному току, авометр, переключатель двухполюсной, соединительные провода.
Задание.
Ознакомьтесь с устройством асинхронного двигателя. Подключив двигатель к генератору трехфазного тока., проведите его испытания.
Метод выполнения работы
Важнейшим достоинством трехфазной системы является возможность создания и широкого использования в практике очень простых и надежных электродвигателей, принцип действия которых основан на использовании трехфазного тока.
Статор трехфазного электродвигателя имеет такое же устройство, как и статор трехфазного генератора. Три обмотки электродвигателя соединяют звездой или треугольником и подключают к трехфазной сети.
Каждая обмотка создает переменное магнитное поле. В любой момент времени модуль индукции магнитного поля В пропорционален силе тока i в катушке. Изменения индукции магнитного поля любой катушки происходят по закону изменения силы тока в ней:
В1 = Вт sin t, B2 = Bmsin(wt—
t, B2 = Bmsin(wt—
 ), В3 = Вm sin(
), В3 = Вm sin(  —
— ).
).
Е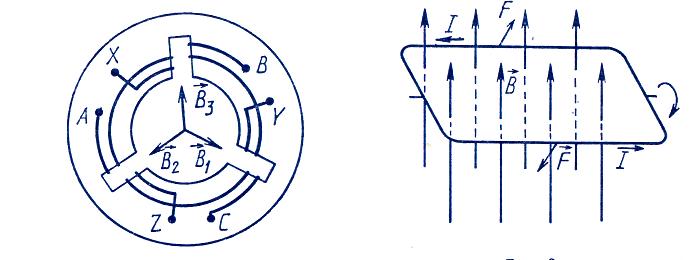 сли бы векторы индукции всех трех магнитных полей были направлены по одной прямой, то суммарная магнитная индукция была бы равна нулю в любой момент времени.
сли бы векторы индукции всех трех магнитных полей были направлены по одной прямой, то суммарная магнитная индукция была бы равна нулю в любой момент времени.
Однако в трехфазном электродвигателе обмотки сдвинуты друг относительно друга по окружности статора на 120° (рис. 1), такие же углы образуют между собой векторы магнитной индукции В\, Bz и Вз.
Выполнив сложение этих векторов, можно убедиться, что модуль вектора магнитной индукции результирующего магнитного поля, созданного тремя катушками, постоянен:В= 1,5 Вт, сам же вектор В вращается в плоскости осей катушек с угловой скоростью со.
Этот вывод можно проверить экспериментально. Если во вращающееся магнитное поле поместить магнитную стрелку или рамку, питаемую постоянным током, то они будут вращаться с той же угловой скоростью, с какой вращается магнитное поле, т. е. синхронно с ним. Это явление используется в синхронных двигателях.
Однако более широко в промышленности применяются асинхронные трехфазные двигатели.
Если во вращающееся магнитное поде поместить замкнутую металлическую рамку на оси, совпадающей с осью вращения поля, то вследствие вращения магнитного поля магнитный поток, пронизывающий металлическую рамку, изменяется. Это приводит к возникновению в рамке ЭДС индукции и индукционного тока. При взаимодействии вращающегося магнитного поля с током в рамке возникают силы Ампера, действующие на каждую сторону рамки. Эти силы поворачивают рамку в направлении вращения поля (рис. 2).
По мере того как скорость вращения рамки приближается к скорости вращения магнитного поля, скорость изменения пронизывающего ее магнитного потока уменьшается, поэтому уменьшается ЭДС индукции и сила тока в рамке. Это приводит к уменьшению момента сил, действующих на рамку.
При равенстве скоростей вращения магнитного поля и рамки ЭДС индукции и ток в рамке равны нулю. Следовательно, и момент сил, вызывающих вращение рамки, становится равным нулю. Момент сил отличен от нуля только при вращении рамки со скоростью, меньшей скорости вращения магнитного поля.
Вращающий момент на валу трехфазного асинхронного электродвигателя возрастает с уменьшением скорости вращения ротора и достигает максимального значения при его остановке.
Наиболее широко применяются асинхронные трехфазные двигатели с короткозамкнутым ротором. В таких машинах обмотка ротора представляет собой систему медных стержней, заложенных в пазы ротора и соединенных с торцов медными кольцами. Обмотку такого типа называют «беличьим колесом». «Беличье колесо» может быть и алюминиевым.
При изменении порядка включения начала и конца любой из обмоток статора направление вращения магнитного поля изменяется на противоположное, поэтому для реверсирования (т. е. изменения направления вращения ротора) трехфазного двигателя достаточно изменить порядок подключения начала и конца одной из обмоток статора к сети трехфазного тока.
Порядок выполнения работы
Ознакомьтесь с конструкцией асинхронного трехфазного двигателя. Соедините его обмотки звездой и подключите к клеммам трехфазного генератора, обмотки которого соединены звездой.
Приведите генератор в действие. Измерьте силу тока в обмотках электродвигателя в момент его запуска и в установившемся режиме.
Переключите обмотки двигателя по схеме треугольника и выполните аналогичные измерения.
Включите в цепь переключатель, с помощью которого можно изменять порядок подключения начала и конца одной из обмоток статора асинхронного двигателя. Осуществите с помощью этого переключателя реверсирование двигателя.
| B1 | B2 | B3 | Bm | F | L | t | I |
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы.
Какое явление используется в синхронных двигателях?
Что будет, если во вращающееся магнитное поле поместить металлическую рамку?
3. Что нужно сделать, чтобы осуществить реверсирование асинхронного двигателя?
4.Что представляет собой “Беличье колесо”?
Оборудование. Образец из стали, алюминия и графита, катушка с током, железный сердечник
Цель. Научиться вычислять магнитные поля в магнетиках и изучить различные свойства магнетиков.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
Вам уже известно, что на кусок железа, помещенный близи катушки с током, действует значительная сила притяжения. Известно также, что сила взаимодействия между двумя катушками с током существенно возрастает, если поместить в них железный сердечник. Аналогичными свойствами обладают, кроме железа, различные сорта стали, а также никель, кобальт и некоторые сплавы:
п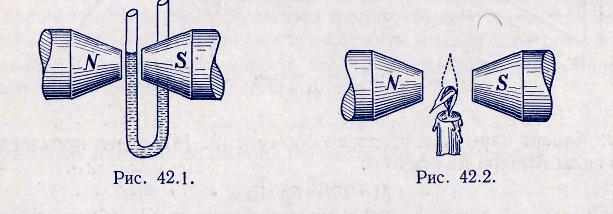 ермаллои, альни, магнико.
ермаллои, альни, магнико.
Все эти вещества называются
ферромагнетиками (от латинского ferrum — железо).
В пятидесятых годах прошлого столетия Фарадей показал, что все вещества обладают магнитными свойствами, но степень и характер их взаимодействия с полем у разных веществ различны. В связи с этим различают вещества с парамагнитными, диамагнитными и ферромагнитными свойствами.
По интенсивности взаимодействия с магнитным полем можно все вещества разбить на два класса. К слабо магнитным веществам относятся все диамагнетики и парамагнетики. Эти вещества при любых температурах очень слабо взаимодействуют с магнитным полем. сильно магнитным веществам относятся ферромагнетики и антиферромагнетики, которые при определенных температурах сильно взаимодействуют с полем.
2. Парамагнетиками называются вещества, которые втягиваются в область более сильного поля. Если в U-образную стеклянную трубку налить парамагнитную жидкость и поместить одно колено между полюсами сильного электромагнита, то жидкость в этом колене поднимется (рис. 42.1). Стерженек из парамагнитного вещества, подвешенный на тонкой нити, ориентируется в магнитном поле вдоль силовых линий.
По своим свойствам парамагнетики несколько напоминают ферромагнетики, но сила их взаимодействия полем в сотни и тысячи раз слабее. Поэтому для наблюдения парамагнитных эффектов необходимы сильные магнитные поля. Парамагнитными свойствами обладают платина, алюминий, вольфрам, все щелочные и щелочно-земельные металлы; из газов — кислород и в слабой степени окись азота.
3. Диамагнетиками называются вещества, которые выталкиваются из магнитного поля.Так, если между полюсами электромагнита зажечь свечу, то пламя вытолкнется из поля (рис. 42.2). Стерженек из диамагнитного вещества, подвешенный на нити в сильном магнитном поле, устанавливается поперек
силовых линий. Заметим, что силы, действующие на диамагнетик в магнитном поле, на один-два порядка меньше сил, действующих на парамагнетик в этом же поле. Поэтому для наблюдения диамагнитных эффектов требуются очень сильные поля. К диамагнетикам относятся почти все газы (кроме кислорода), вода, серебро, золото, медь, алмаз, графит, висмут, многие органические соединения.
Магнитный момент атома.В начале XIX в. Ампер пришел к выводу, что магнитные свойства вещества можно объяснить, если допустить, что атомы представляют собой микроскопические элементарные магниты. Однако обосновать происхождение элементарных магнитных моментов Ампер не смог. Ядерная модель строения атома, которой мы уже пользовались для объяснения механизма деформационной поляризуемости (§ 38.5), поможет нам понять происхождение магнитных моментов атомов. В самом деле, электрон, циркулируя в атоме, представляет собой элементарный ток, обладающий магнитным моментом рорб. Кроме того, циркулирующий по орбите электрон имеет момент импульса, называемый орбитальным моментом
импульса Lop6. Согласно (40.28) между этими величинами должна существовать следующая связь: Pmорб= Здесь те — масса покоя электрона, е — его заряд. Магнитный момент атома складывается из магнитных моментов электронов, движущихся вокруг ядра, и магнитного момента самого ядра. Однако опыт показывает, что магнитный момент ядра примерно в 2000 раз меньше магнитного момента электрона (§ 80.2). Поэтому при изучении магнитных свойств вещества пренебрегают магнитным моментом ядра и считают, что магнитный момент атома равен векторной сумме магнитных моментов электронов, циркулирующих вокруг ядра. Попытаемся оценить величину этого магнитного момента. Пусть в пространстве выделено некоторое направление, например ось г. Это может означать, что вдоль этой оси направлено какое-либо магнитное поле. В квантовой механике доказывается, что проекция орбитального момента импульса на заданное направление может принимать только некоторые, вполне определенные значения:
Здесь те — масса покоя электрона, е — его заряд. Магнитный момент атома складывается из магнитных моментов электронов, движущихся вокруг ядра, и магнитного момента самого ядра. Однако опыт показывает, что магнитный момент ядра примерно в 2000 раз меньше магнитного момента электрона (§ 80.2). Поэтому при изучении магнитных свойств вещества пренебрегают магнитным моментом ядра и считают, что магнитный момент атома равен векторной сумме магнитных моментов электронов, циркулирующих вокруг ядра. Попытаемся оценить величину этого магнитного момента. Пусть в пространстве выделено некоторое направление, например ось г. Это может означать, что вдоль этой оси направлено какое-либо магнитное поле. В квантовой механике доказывается, что проекция орбитального момента импульса на заданное направление может принимать только некоторые, вполне определенные значения:
Lорбz = mh,
где h — постоянная Планка, т — целое число. Пользуясь соотношением (42.1), получим для проекции орбитального магнитного момента, которую мы обозначим :
Pорьmz= =m
=m Величина
Величина  называется магнетоном Бора. Она составлена из мировых констант — заряда и массы электрона и постоянной Планка — и поэтому тоже является мировой константой.
называется магнетоном Бора. Она составлена из мировых констант — заряда и массы электрона и постоянной Планка — и поэтому тоже является мировой константой.
Магнетон Бора — это минимальное отличное от нуля значение проекции магнитного момента электрона на произвольное направление. А так как магнитный момент атома есть векторная сумма магнитных моментов электронов, то мы можем утверждать, что проекция магнитного момента атома на некоторую ось либо равна нулю, либо кратна магнетону Бора. Ниже мы увидим, что опыты подтверждают эту оценку.
Величины, характеризующие магнитное поле в веществе
1. Для характеристики степени поляризации диэлектрика в электрическом поле была введена особая физическая величина — вектор поляризации, равный дипольному моменту единицы объема поляризованного диэлектрика. Аналогично введем величину, характеризующую степень намагниченности вещества в магнитном поле,— вектор намагниченности. Вектором намагниченности М называется магнитный момент единицы объема намагниченного вещества. Чтобы его вычислить, необходимо найти векторную сумму магнитных моментов всех атомов, заключенных в единице объема намагниченного вещества. Для простоты рассуждений положим, что вещество однородное и все его атомы имеют один и тот же магнитный момент рт. Тогда вектор намагниченности
M= =npm где п — концентрация атомов. Единица намагниченности совпадает с единицей напряженности магнитного поля: А/м=[H].
=npm где п — концентрация атомов. Единица намагниченности совпадает с единицей напряженности магнитного поля: А/м=[H].
2. Ограничимся рассмотрением простейшего случая, когда однородное и изотропное вещество сплошь заполняет магнитное поле. Это можно реализовать, если на тороидальный сердечник из исследуемого вещества равномерно намотать обмотку, по которой течет ток. Вещество сердечника, естественно, намагнитится за счет действия магнитного поля тока. Оказывается, что если вещество представляет собой парамагнетик или диамагнетик, то его вектор намагниченности пропорционален напряженности намагничивающего поля
М = ктН. (42.6)
Коэффициент пропорциональности хт в выражении (42.6) называется магнитной восприимчивостью вещества. Читатель легко убедится, что магнитная восприимчивость является безразмерной величиной.
3. Вектор намагниченности определяет индукцию магнитного поля Bвещ, создаваемого намагниченным веществом. По аналогии с тем, как связана индукция поля токов с напряженностью этого поля (BTOK= H), напишем соотношение между индукцией поля вещества и его намагниченностью:Bвещ=
H), напишем соотношение между индукцией поля вещества и его намагниченностью:Bвещ= 0M. Индукция магнитного поля в веществе, которое сплошь заполняет магнитное поле, представляет собой векторную сумму индукций поля намагничивающих токов и поля намагниченного вещества:
0M. Индукция магнитного поля в веществе, которое сплошь заполняет магнитное поле, представляет собой векторную сумму индукций поля намагничивающих токов и поля намагниченного вещества:
В = Вток +Ввещ = (Н+М). На основании имеем B=
(Н+М). На основании имеем B= (H+
(H+ H)=
H)= H
H
Величина

называется магнитной проницаемостью вещества.
Диамагнетизм П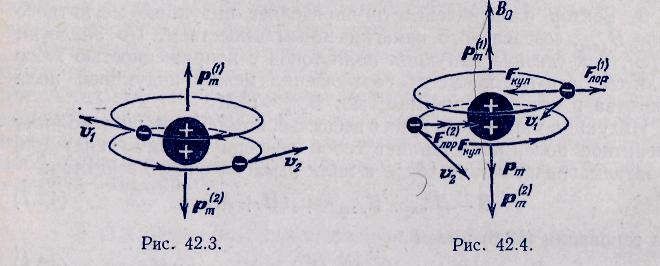 опытаемся выяснить механизм диамагнитного эффекта. Для
опытаемся выяснить механизм диамагнитного эффекта. Для
анализа используем модель атома гелия. Ядро этого атома имеет заряд q=+2e, а вокруг ядра обращаются два электрона. Опыт показывает, что атом гелия не имеет магнитного момента. Это можно объяснить, если мы предположим, что оба электрона обращаются вокруг ядра с одинаковой скоростью по одинаковым орбитам, но в противоположных направлениях. Тогда их орбитальные магнитные моменты будут равны по величине, но противоположны по знаку,
и суммарный магнитный момент атома окажется равным нулю (рис. 42.3).Поместим атом гелия в магнитное поле с индукцией В0= 0Н. Для простоты рассуждений положим, что вектор индукции перпендикулярен плоскости орбиты электрона (рис. 42.4). В этом случае
0Н. Для простоты рассуждений положим, что вектор индукции перпендикулярен плоскости орбиты электрона (рис. 42.4). В этом случае
на электрон действуют две силы — кулоновская сила притяжения к ядру и сила Лоренца. Их равнодействующая сообщает электрону центростремительное ускорение. Уравнения движения для обоих электронов примут вид
Fкул- Fлор= 
Следует обратить внимание на тот факт, что в этих уравнениях мы полагаем, что под действием магнитного поля меняется только скорость движения электрона, но не радиус орбиты.
3. Из уравнений (42.10) следует, что под действием магнитного поля скорость движения первого электрона уменьшилась, второго возросла. Соответственно изменяются и их магнитные моменты. Таким образом, под действием внешнего магнитного поля у атома наводится (индуцируется) магнитный момент
Pm=
Заметим, что индуцированный магнитный момент рт направлен противоположно направлению вектора индукции внешнего поля (рис. 42.4). Разность скоростей найдем из (42.10), если вычтем из нижнего равенства верхнее:
eB0(v2 + v1) =
или после сокращений
v2-v1= (42.12)
(42.12)
Подставив в (42.11), получим для индуцированного магнитного момента
(42.13)
Учитывая, что векторы рт и Н направлены противоположно, перепишем (42.13) в векторном виде:
Рт=- Н
Н
.4. Вектор намагниченности, согласно (42.5), равен
M=npm=-
Итак, здесь вектор намагниченности действительно пропорционален напряженности намагничивающего поля (см. (42.6)). Магнитная восприимчивость является отрицательной величиной:

Парамагнетизм.
1. Рассмотренный в предыдущем параграфе механизм намагничивания диамагнетиков сводится к наведению дополнительного магнитного момента у атома под действием внешнего магнитного поля. Это явление характерно для атомов любого вещества, следовательно, все вещества должны обладать диамагнитными свойствами. Откуда же берутся парамагнетики?
Оказывается, что в отличие от диамагнетиков, у которых магнитные моменты электронов внутри атома скомпенсированы, атомы парамагнетиков имеют не скомпенсированные магнитные моменты. Под действием внешнего магнитного поля эти магнитные моменты поворачиваются, стремясь расположиться вдоль силовых линий поля. Тепловое движение, естественно, расстраивает этот порядок. Мы видим, что механизм намагничивания парамагнетиков вполне аналогичен механизму поляризации диэлектриков с полярными молекулами (§ 38.6). Если провести такие же рассуждения, как и при выводе формулы (38.25), получим выражение для намагниченности парамагнетиков:
M=
Магнитная восприимчивость парамагнетиков является положительной величиной:

Как видно, при неизменной концентрации атомов (т. е. при неизменной плотности вещества) магнитная восприимчивость парамагнетиков меняется обратно пропорционально абсолютной температуре(закон Кюри):
xm=const/T
Это явление подтверждается экспериментально.
Заметим, что выражение (42.16) справедливо при условии, если pmB0/kT .l, т. е. если энергия диполя
.l, т. е. если энергия диполя  магнитном поле
магнитном поле  т=ртВ0 много меньше энергии теплового движения частицы R=kT. Поскольку pm=9,27-10~24 А-м2, а максимально достижимая индукция магнитного поля Вмаксда 1,3 Тл, то при комнатных температурах это условие всегда выполняется. Лишь при очень низких температурах можно получить
т=ртВ0 много меньше энергии теплового движения частицы R=kT. Поскольку pm=9,27-10~24 А-м2, а максимально достижимая индукция магнитного поля Вмаксда 1,3 Тл, то при комнатных температурах это условие всегда выполняется. Лишь при очень низких температурах можно получить
pmBu/kT= 1;
для этого парамагнетик следует охладить до температуры T=
 =1K
=1K
т. е. близкой к абсолютному нулю. В этом случае намагниченность парамагнетика будет близка к насыщению, так как все магнитные моменты атомов расположатся вдоль поля, а слабое тепловое движение этот порядок разрушить не сможет.
Ферромагнетизм. Точка Кюри.
1. В отличие от парамагнетиков и диамагнетиков, у которых вектор намагниченности пропорционален напряженности намагничивающего поля, у ферромагнетиков намагниченность является весьма сложной нелинейной функцией напряженности! Для никеля эта зависимость изображена на рис. 42.5. Для удобства изображения масштаб нарушен: область напряженности поля от 0,1-103 до 2-103 А/м растянута. Как видно из рисунка, намагниченность никеля сначала быстро нарастает с ростом напряженности магнитного поля. Затем наступает магнитное насыщение, когда намагниченность уже
о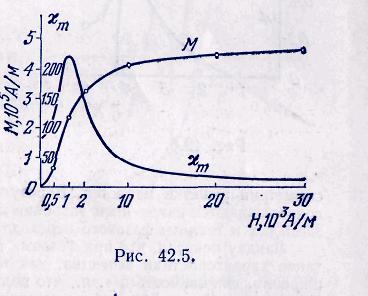 т величины намагничивающего поля.
т величины намагничивающего поля.
Поскольку намагниченность ферромагнетика не пропорциональна напряженности намагничивающего поля, выражения (42.6) и (42.8) теряют смысл. Формально, однако, ими можно пользоваться, учитывая, что для ферромагнетиков магнитная восприимчивость
 =М/H
=М/H
и магнитная проницаемость  =В/
=В/ H являются не посто намагничивающего поля.
H являются не посто намагничивающего поля.
2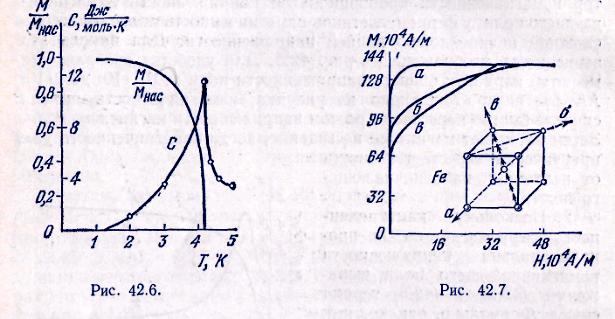 . Следующее важное отличие ферромагнетиков заключается в том, что если парамагнитные или диамагнитные свойства вещества проявляются в любом агрегатном состоянии, то ферромагнитные свойства наблюдаются только у кристаллов. В жидком или газообразном состоянии ферромагнитные вещества ведут себя как обычные парамагнетики. Отсюда следует, что ферромагнитные свойства некоторых веществ определяются не особыми свойствами их атомов — последние ничем не отличаются от атомов парамагнетиков,— а особой структурой их кристаллической решетки. При изменении структуры решетки должны меняться и магнитные свойства ферромагнетиков. Опыт подтверждает это предположение.
. Следующее важное отличие ферромагнетиков заключается в том, что если парамагнитные или диамагнитные свойства вещества проявляются в любом агрегатном состоянии, то ферромагнитные свойства наблюдаются только у кристаллов. В жидком или газообразном состоянии ферромагнитные вещества ведут себя как обычные парамагнетики. Отсюда следует, что ферромагнитные свойства некоторых веществ определяются не особыми свойствами их атомов — последние ничем не отличаются от атомов парамагнетиков,— а особой структурой их кристаллической решетки. При изменении структуры решетки должны меняться и магнитные свойства ферромагнетиков. Опыт подтверждает это предположение.
Оказывается, что для каждого ферромагнетика имеется определенная температура — точка Кюри, выше которой ферромагнитные свойства исчезают и вещество становится обычным парамагнетиком. Для железа точка Кюри составляет 770 °С, для никеля 360°С, а для пермаллоя (сплав 70% Fe и 30% №) всего лишь 70 °С.4. Как показал Л. Д. Ландау, точка Кюри у ферромагнетиков — это температура фазового перехода второго рода.
При фазовых переходах первого рода меняется структура вещества; например, при плавлении кристалла дальний порядок меняется на ближний. В результате меняется внутренняя энергия и энтропия тела, что требует затраты некоторой энергии — теплоты фазового перехода (см. гл. 36). Фазовые переходы второго рода, например исчезновение ферромагнитных свойств вещества при переходе через точку Кюри, не сопровождаются изменением агрегатного состояния. В частности, при этом кристаллическая решетка не разрушается, хотя тип симметрии решетки меняется. В результате фазовые переходы второго рода не сопровождаются изменением энтропии и внутренней энергии тела, следовательно, здесь нет и теплоты фазового перехода.
Ландау показал, что при фазовых переходах второго рода скачком меняются такие характеристики вещества, как теплоемкость, коэффициент теплового расширения, сжимаемость и т. п., что подтверждается экспериментом. На рис. 42.6 показаны графики изменения намагниченности и теплоемкости некоторого вещества. Как видно, при температуре 4,2 К намагниченность резко падает; следовательно, эта температура есть точка Кюри для данного вещества. При этой температуре теплоемкость вначале быстро возрастает, а затем падает.
3. Ферромагнетизм присущ только кристаллам, а последние обладают анизотропией, поэтому монокристалл ферромагнитного вещества должен обладать анизотропией намагничивания — его магнитные свойства должны быть разными в разных направлениях. Опыт подтверждает это предположение.
Н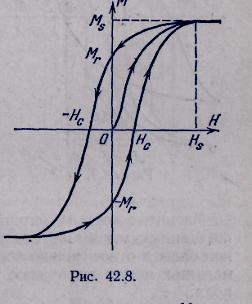 а рис. 42.7 изображены графики намагниченности монокристалла железа, имеющего решетку типа объемно-центрированного куба. Оказывается, что в направлении ребра куба намагниченность вещества при данном значении напряженности поля наибольшая (а), меньше она в направлении диагонали грани (б) и наименьшая намагниченность — в направлении пространственной диагонали куба (б). Поэтому ребро куба называется направлением легкого намагничивания, а диагональ куба — направлением трудного намагничивания. Естественно, что в поликристалле анизотропия намагниченности не проявляется, поскольку отдельные микрокристаллики ориентированы беспорядочно.
а рис. 42.7 изображены графики намагниченности монокристалла железа, имеющего решетку типа объемно-центрированного куба. Оказывается, что в направлении ребра куба намагниченность вещества при данном значении напряженности поля наибольшая (а), меньше она в направлении диагонали грани (б) и наименьшая намагниченность — в направлении пространственной диагонали куба (б). Поэтому ребро куба называется направлением легкого намагничивания, а диагональ куба — направлением трудного намагничивания. Естественно, что в поликристалле анизотропия намагниченности не проявляется, поскольку отдельные микрокристаллики ориентированы беспорядочно.
Гистерезис.
1. Характерным свойством ферромагнетиков является гистерезис. Явление заключается в том, что намагниченность ферромагнетика зависит не только от напряженности намагничивающего поля в данный момент, но и от предварительного намагничивания образца. Поэтому вообще нельзя указать, какая намагниченность ферромагнетика, соответствует данному значению
напряженности намагничивающего поля, если не известно, в каком состоянии он до этого находился. То же, естественно, относится к значениям магнитной восприимчивости и проницаемости.
График рис. характеризует ход первоначальной намагниченности, когда ферромагнетик был сначала нагрет выше точки Кюри и тем самым полностью размагничен, а затем охлажден и подвергнут намагничиванию. Совершенно иной вид будет иметь кривая намагниченности, если ферромагнетик был уже ранее намагничен.
2. Изготовим сердечник в форме тороида из размагниченного ферромагнетика и обмотаем его равномерно проводником, ток в обмотке, мы тем самым меняем напряженность намагничивающего поля. Пусть напряженность поля возрастет до значения Hs (рис. 42.8). Этому значению поля соответствует намагниченность насыщения, равная Ms. Будем уменьшать ток в обмотке, уменьшая тем самым напряженность намагничивающего поля. Мы убедимся, что намагниченность сердечника в процессе размагничивания остается все время большей, чем в процессе намагничивания.
Когда ток в обмотке станет, равен нулю, исчезнет и намагничивающее поле. Но намагниченность ферромагнетика не обратится в нуль — сердечник сохранит некоторую остаточную намагниченность Мг. И только в том случае, когда по обмотке будет пропущен ток обратного направления и возникнет поле с напряженностью Нс., намагниченность сердечника обратится в нуль. Напряженность размагничивающего поля Нс. называется коэрцитивной силой.
Кривая, изображенная на рис. называется гистерезисной петлей.
3. В зависимости от химического состава, а также от характера тепловой и механической обработки материала (закалка, отжиг, прокат, холодная штамповка и т. п.) встречаются ферромагнетики с различными свойствами. Вещества с малыми значениями коэрцитивной силы называются «мягкими» магнитными материалами, высококоэрцитивные материалы — «жесткими». На рис. 42.9 изображены
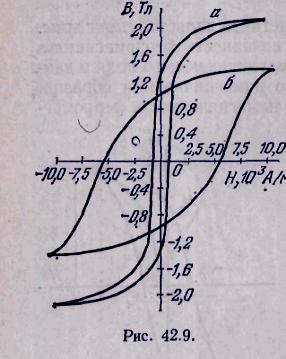 гистерезисные петли двух материалов: магнитно-мягкого железа (а) и высококоэрцитивной закаленной стали (б).
гистерезисные петли двух материалов: магнитно-мягкого железа (а) и высококоэрцитивной закаленной стали (б).
Форма гистерезисной петли определяет область применения того или иного ферромагнетика. «Мягкие» магнитные материалы применяются для изготовления сердечников электромагнитов, где важно иметь большое ' значение максимальной индукции поля и малую коэрцитивную силу. Эти же материалы используются в качестве сердечников трансформаторов и машин переменного тока (генераторов, двигателей): благодаря малой коэрцитивной силе они легко перемагничиваются. Такие же требования предъявляются к сердечникам магнитов ускорителей.
Магнитно-жесткие материалы используются для изготовления постоянных магнитов. Благодаря большому значению коэрцитивной силы и относительно большой остаточной намагниченности эти магниты могут длительное время создавать сильные магнитные поля.
Постоянные магниты из высококоэрцитивных сплавов применяются в магнитоэлектрических измерительных приборах, в электродинамических репродукторах («динамиках») и микрофонах, в небольших генераторах (например, велосипедных), в микроэлектродвигателях и т. п.
Доменная структура ферромагнетиков1. Особенности ферромагнетиков можно объяснить, следуя классической теории ферромагнетизма, предложенной П. Вейссом. Согласно этой теории, при температурах ниже точки Кюри ферромагнетик состоит из микроскопических областей, называемых доменами, в каждой из которых магнитные моменты атомов расположены строго в одном направлении, соответствующем направлению легкого намагничивания (§ 42.6). Тем самым каждый домен оказывается намагниченным до насыщения независимо от наличия внешнего магнитного поля и от его величины.
Размеры доменов достигают 10~2-10~3 см, вследствие чего их можно наблюдать в микроскоп. Для того чтобы увидеть домены, на полированную поверхность ферромагнетика наносят каплю масла, в которой взвешены мельчайшие частицы ферромагнитного порошка
(метод Акулова — Биттера).
Частицы ферромагнитного порошка концентрируются на границах доменов, где магнитное поле наиболее неоднородно (рис. 42.10).
П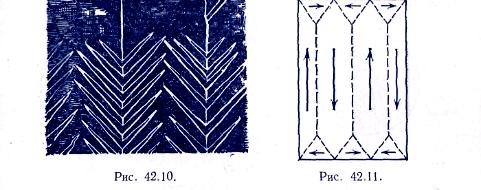 ри отсутствии внешнего магнитного поля домены в монокристалле располагаются так, что их магнитные поля замыкают друг друга и суммарное внешнее магнитное поле оказывается равным нулю.
ри отсутствии внешнего магнитного поля домены в монокристалле располагаются так, что их магнитные поля замыкают друг друга и суммарное внешнее магнитное поле оказывается равным нулю.
На рис. схематически изображены эти домены. Стрелками показаны направления векторов намагниченности внутри доменов. Как показали Л. Д. Ландау и Е. М. Лифшиц, такая система доменов в монокристалле характеризует состояние с минимальной энергией магнитного поля, что с точки зрения законов термодинамики обеспечивает устойчивое равновесие этой системы.
2. Объясним на основе этих представлений механизм намагничивания поликристаллического образца. Поликристалл состоит из отдельных зерен, у которых направления легкого намагничивания ориентированы беспорядочно. Каждое зерно разбивается на несколько доменов, направленных вдоль линии легкого намагничивания (рис. 42.12, а).
П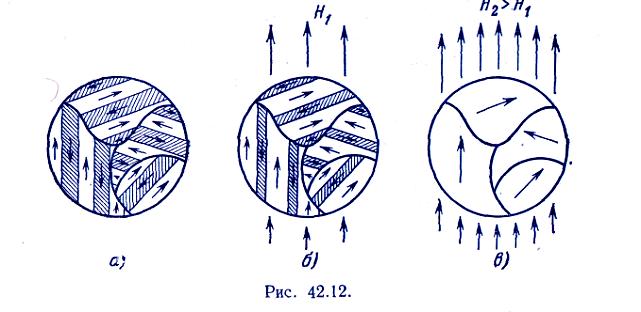 ри включении слабого внешнего магнитного поля всегда найдется множество доменов, у которых направление вектора намагниченности совпадет с направлением внешнего поля. Эти домены будут обладать минимумом энергии и поэтому окажутся в состоянии устойчивого равновесия. Соседние домены обладают максимумом энергии. Поэтому энергетически выгодно, если магнитные моменты некоторых атомов изменят свое направление и присоединятся к тем доменам, энергия которых минимальна. Этот процесс называется смещением границ доменов (рис. 42.12, б).
ри включении слабого внешнего магнитного поля всегда найдется множество доменов, у которых направление вектора намагниченности совпадет с направлением внешнего поля. Эти домены будут обладать минимумом энергии и поэтому окажутся в состоянии устойчивого равновесия. Соседние домены обладают максимумом энергии. Поэтому энергетически выгодно, если магнитные моменты некоторых атомов изменят свое направление и присоединятся к тем доменам, энергия которых минимальна. Этот процесс называется смещением границ доменов (рис. 42.12, б).
По мере роста напряженности внешнего магнитного поля, границы доменов сдвигаются все сильнее. При этом стенки доменов начинают встречать на своем пути дефекты кристалла — дислокации, внедрения и т. п. (§ 32.4). Эти дефекты препятствуют изменению направления магнитного момента у атомов, расположенных вблизи дефекта (препятствуют перемещению стенок домена). По мере роста поля потенциальная энергия атомов (магнитных диполей) вблизи дефекта возрастет настолько, что превысит энергию активации (§ 34.3). В этом случае магнитные моменты атомов вблизи дефекта скачком изменят свое направление на противоположное — иными словами, стенка домена скачком срывается с места и движется до следующего дефекта. Таким образом, процесс намагничивания поликристаллического вещества идет не плавно, а скачками. Это явление называется эффектом Баркгаузена.
Оно может быть обнаружено экспериментально. К пучку из никелевой проволоки подносят магнит; происходит скачкообразное намагничивание никеля, что приводит к скачкообразному изменению магнитного поля. Благодаря явлению электромагнитной индукции (см. гл. 43) в обмотке, навитой на никелевый пучок, возникают импульсы тока, которые хорошо слышны в телефоне.
Скачкообразный характер процесса намагничивания поликристаллического ферромагнетика приводит к необратимым потерям энергии (перемещение дислокаций и других дефектов, возникновение упругих волн, энергия которых переходит во внутреннюю, и т. п.). Следовательно, и процесс намагничивания в сильных полях происходит необратимо. При уменьшении магнитного поля структура вещества не будет восстанавливаться: домены при размагничивании будут иметь другую форму и ориентировку по сравнению с процессом намагничивания. Это и является причиной гистерезисного эффекта.
3. В достаточно сильных полях все стенки доменов сдвинутся к границам кристаллических зерен, и каждое зерно окажется намагниченным вдоль того направления легкого намагничивания, которое составляет наименьший угол с направлением внешнего поля (рис. 42.12, в). Если еще больше усилить напряженность намагничивающего поля, то магнитные моменты зерен начнут поворачиваться, выстраиваясь вдоль поля. Этот процесс требует сильных полей, в результате чего в этой области намагниченность меняется мало и рост кривой намагничивания замедляется.
Наконец, когда магнитные моменты всех зерен выстроятся вдоль поля, наступает магнитное насыщение — с ростом внешнего поля намагниченность вещества перестает возрастать.
4. Как видно, используя представления о доменной структуре ферромагнетиков, можно объяснить все особенности процесса их намагничивания. Точка Кюри оказывается той температурой, выше которой происходит  разрушение доменной структуры.
разрушение доменной структуры.
Остается ответить на два вопроса. Прежде всего, нужно объяснить, какие силы приводят к тому, что внутри домена магнитные моменты всех атомов самопроизвольно выстраиваются вдоль направления легкого намагничивания. А затем нужно найти причины того, почему одни вещества обладают ферромагнитными свойствами, а другие нет. Ответ на эти вопросы смогла дать только квантовая теория магнитных явлений.
Выполнение работы.
Посчитайте орбитальный магнитный момент и момент импульса.
Определите вектор намагниченности, а также магнитную проницаемость и восприимчивость.
Вычислите температуру образцов в Кельвинах.
Постройте график зависимости вектора намагниченности от напряженности магнитного поля.
Занесите данные в таблицу и сделайте вывод.
Ответьте на контрольные вопросы.
Вариант 1
| Pm | Lорб | m |
| M | n |
| H | B |
|
| r | T |
|
|
| 2 |
|
| 2.7 |
|
| 1.3 |
|
| 0.5 |
|
Контрольные вопросы.
Что называется ферромагнетиками, диамагнетиками, парамагнетиками и вектором намагниченности?
Расскажите о механизме диамагнитного эффекта.
Расскажите о намагниченности парамагнетиков.
Расскажите свойстве ферромагнетиков -гистерезисе. Нарисуйте петлю гистерезиса для жестких и мягких ферромагнетиков.
Расскажите о смещении границ доменов и об эффекте Баркгаузена







 t, c
t, c , В
, В









