Интегрированный урок по математике и информатике по теме «Геометрические тела» с использованием метода проектов и кейс-технологии

Открытый интегрированный урок по математике и информатике

по теме «Геометрические тела»

с использованием метода проектов и кейс-технологии.

Дата 6.04.2023 г.

Курс II Группа № 7 «Сварщик»

ФИО преподавателей:Украинская Светлана Альбертовна (преподаватель информатики); Сметанина Наталья Владимировна (преподаватель математики)

Вид урока: интегрированный (бинарный) урок.

Тип урока: урок обобщения и систематизации.

Форма урока: фронтальная, работа в малых группах (парах)

Цели урока:

Образовательные. Обобщить понятия геометрических тел, их названия, их свойства и где они применяются, применение полученных навыков при решении задач. Показать межпредметные связи.

Развивающие. Проверить знания, умения и навыки при работе с компьютером (развитие творческих способностей)

Воспитательные. Всесторонне способствовать развитию интереса к информатике и математике.

Методы обучения: объяснительно-иллюстрированный (информационно-рецептивный), проектный метод, кейс-метод

Средства обучения: компьютерный класс, мультимедийное оборудование, кейс.

Межпредметная связь: математика, информатика, предмет спец.цикла по профессии «Сварщик»

Компетенции

ОК 4. Осуществлять поиск информации, необходимой для эффективного выполнения профессиональных задач.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, клиентами.

План урока.

1. Организационный момент. Совместное целеполагание и мотивация(2 мин).

2. Актуальность урока. (2 мин)

3. Определение цели и задач мини-проекта. (3 мин.)

4. Практическая часть. Составление мини-проекта каждой парой.(21мин)

5. Защита проектов.(15 мин.)

6. Домашнее задание.(1 мин)

7. Итог урока.(1 мин)

Ход урока

Преподаватель информатики

1. Сегодня у нас с вами необычный интегрированный урок математики и информатики. На протяжении многих лет эти предметы дополняли друг друга. Невозможно сейчас представить информатику без математики, а уроки математики становятся более интересными и насыщенными с использованием информационных технологий. Поэтому сегодня мы посмотрим, как с помощью навыков владения компьютером можем обобщить или систематизировать необходимый материал. Посмотрите на слайд №1 . Что там изображено? (Геометрические тела) . При помощи какой программы можно было все эти фигуры продемонстрировать? (PowerPoint). Постарайтесь сформулировать тему нашего урока и его цели.

Тема урока – «Геометрические тела»

Цели – обобщить материал по теме «Геометрические тела». Создать мини-проект

Преподаватель математики

2)Для решения геометрическихи технических задач необходимо твердое владение теоретическим материалом, а именно, свойствами заданных плоских и пространственных фигур, применять эти свойства в ходе вычислений. Для успешного решения этих задач необходимо иметь прочные базовые знания, что поможет наметить план решения. Решение геометрических задач требует иметь необходимые умения логически мыслить, быть внимательным. Дальше мы более подробно рассмотрим каждое геометрическое тело и определим для каждого из них особенности и свойства, необходимые для решения задач.

3)Преподаватель информатики

Для этого вы разделились на пары по 2 человека. Давайте проведём жеребьёвку. Каждая пара будет создавать мини проект по выбранному жребием геометрическому телу. Результатом составленного вами мини проекта будет презентация, которую необходимо будет защитить.

Цель мини проекта: Составить презентацию, в которой будут отображены внешний вид геометрического тела, его свойства, где встречается в жизни.

Задачи:

1) Используя любой графический редактор создать изображение геометрического тела.

2) Сформулировать определение данного геометрического тела.

3) Привести примеры из жизни.

4)Записать необходимые формулы для вычисления площади поверхности и объёма.

5) Оформить мини-проект в форме презентации, используя программу PowerPoint.

Для каждой пары будет выдан кейс(Приложение 1), включающий в себя:

1.Задачи мини-проекта

2. Материалы с изображениями, которые находятся на диске F:\16группа

3. Краткий справочный материал

4. Рабочее место с необходимым программным обеспечением.

После того как презентация будет создана, необходимо сохранить ее на диске F:\16группаи скинуть на флеш-носитель.

4) Практическая работа на компьютере. Составление мини проекта.

5) Защита проектов. Выступление представителя от группы.

6) Домашнее задание.

По математике:

Решите следующие задачи:

1. Боковая поверхность цилиндра равна 24π. Высота цилиндра 4. Найти диаметр основания.

2. Сторона основания правильной шестиугольной призмы равна 6, высота 5. Найти боковую поверхность призмы.

3. Найти площадь поверхности правильной четырёхугольной пирамиды, сторона основания которой равна 18 и высота равна12.

По информатике:

Создайте презентацию с элементами анимации по любому другому геометрическому телу и пришлите её на электронную почту преподавателя – inf38@mail.ru

7) Итоги урока.

Сегодня на уроке мы обобщили материал по теме "Геометрические тела". Получили материал в виде презентации, которым вы можете воспользоваться при подготовке к домашнему заданию.Далее проводится рефлексия, включающая в себя выставление оценок и отношение учащихся к уроку (Приложение 2).

Приложение 1

Кейс по теме «Создание мини-проекта по теме «Геометрические тела»»

1. Задачи мини-проекта:

1) Используя любой графический редактор создать изображение геометрического тела.

2) Сформулировать определение данного геометрического тела.

3) Привести примеры из жизни.

4)Записать необходимые формулы для вычисления площади поверхности и объёма.

5) Оформить мини-проект в форме презентации, используя программу PowerPoint.

2.На рабочем месте учащегося на диске F:\16группа собрана коллекция картинок по использованию геометрических тел в жизни.

3. Справочный материал

Многогранники.

Многогранником называется геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников. 

Выпуклым называется многогранник, если он расположен по одну сторону плоскости, проведённой через любой многоугольник, образующий поверхность данного многогранника.

М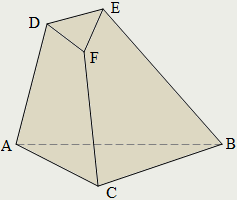 ногоугольники, составляющие поверхность многогранника, называются его гранями; стороны многоугольников – рёбрами; вершины – вершинами многогранника

ABC, DEF, ABED, BCFE, ACFD – грани;

AB, BC, AC, DE, EF, DF, AD, BE, CF – рёбра;

A, B, C, D, E, F – вершины многогранника ABCDEF.

Теорема Эйлера для многогранников:

Если V — число вершин выпуклого многогранника, R — число его ребер и G — число граней, то верно равенство:

V – R + G = 2.

Призма

Призмой называется многогранник, состоящий из двух плоских многоугольников, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники называются основаниями призмы, а отрезки, соединяющие их соответствующие вершины – боковыми рёбрами призмы.

Основания призмы равны и лежат в параллельных плоскостях.

Боковые рёбра призмы равны и параллельны.

Поверхность призмы состоит из двух оснований и боковой поверхности.

В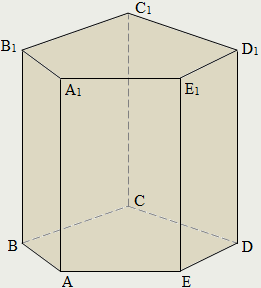 ысотой призмы называется любой из перпендикуляров, проведённых из точки одного основания к плоскости другого основания призмы.

Призма называется п-угольной, если её основание – п-угольник.

АВСA1В1С1 – треугольная призма;

ΔАВС и ΔA1В1С1 – основания;

АA1, ВВ1, СС1 – боковые рёбра;

АA1В1В, АA1С1С, ВВ1С1С – боковые грани;

A1О – высота призмы;

Призма называется прямой, если её рёбра перпендикулярны плоскостям оснований. В противном случае призма называется наклонной.

Боковые грани прямой призмы – прямоугольники.

Боковое ребро прямой призмы является её высотой.

Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы:Sб = Pосн·АА1.

Прямая призма называется правильной, если её основания являются правильными многоугольниками.

П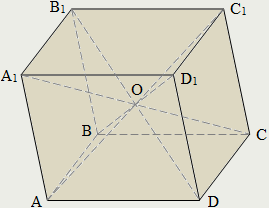 араллелепипед

Призма, в основании которой лежит параллелограмм, называется параллелепипедом.

У параллелепипеда все грани – параллелограммы.

Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.

У параллелепипеда противолежащие грани параллельны и равны.

Диагональю параллелепипеда называется отрезок, соединяющий вершины параллелепипеда, не лежащие в одной его грани.

Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.

Точка пересечения диагоналей параллелепипеда является его центром симметрии.

Прямоугольный параллелепипед

Прямоугольным параллелепипедом называется такой прямой параллелепипед, восновании которого лежит прямоугольник.

Все грани прямоугольного параллелепипеда являются прямоугольниками.

Длины рёбер прямоугольного параллелепипеда, выходящих из одной вершины, называются его измерениями или линейными размерами.

У прямоугольного параллелепипеда три измерения.

В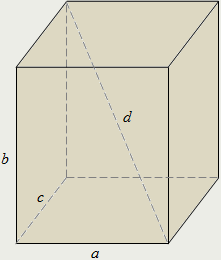 прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений:

d² = a² + b² + c².

В прямоугольном параллелепипеде верно:

для площади полной поверхности:

Sп = 2·(ab+bc+ac);

для объёма:

V = abc.

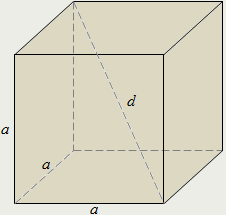
Куб.

Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.

Диагональ куба в квадратный корень из трёх раз больше его стороны:

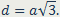
Площадь полной поверхности куба

Sп = 6·a²,   Sп = 2·d²,

Объём куба

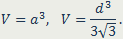
Пирамида

П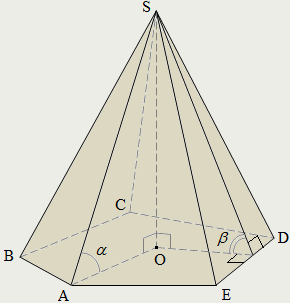 ирамидой (например, SABCDE) называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE) – основания пирамиды, точки (S), не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.

Отрезки (SA, SB, SC, SD, SE), соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.

Поверхность пирамиды состоит из основания  и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды:

ΔSAB, ΔSBC, ΔSCD, ΔSDE, ΔSEA – боковые грани.

Боковой поверхностью пирамиды называется сумма площадей ее боковых граней. 

Высотой пирамиды называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания.

Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром.

Объём пирамиды равен трети произведения площади основания на высоту пирамиды:

V = 1/3·Sоснh.

Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания:

Sп = Sб + Sосн. 

Ц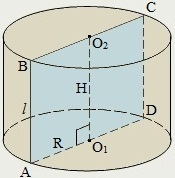 илиндр

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. 

Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называется боковой поверхностью цилиндра.

Высотой цилиндра называется расстояние между плоскостями его оснований.

Другая часть, ограниченная параллельными плоскостями – это основания цилиндра.

У цилиндра: основания равны; образующие параллельны и равны.

Объём  цилиндра равен произведению площади основания на высоту: V = SH.

Прямой круговой цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.

Радиусом цилиндра называется радиус его основания.

Осью цилиндра называется прямая, проходящая через центры его оснований. Ось цилиндра параллельна образующим.

Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра (прямого кругового цилиндра) является прямоугольник.

Боковая поверхность прямого кругового цилиндра равна произведению длины окружности основания на высоту: Sбок = 2πRH.

Полная поверхность цилиндра вычисляется по формуле: Sп = Sбок + 2Sосн = 2πR(H + R).

Объём прямого кругового цилиндра вычисляется по формуле V = πR²H.

К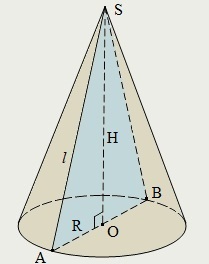 онус

Конической поверхностью называется поверхность, образуемая движением прямой, проходящей всё время через неподвижную точку вдоль данной линии.

Эта линия называется направляющей, двигающаяся прямая, в каждом своём положении, – образующей, а неподвижная точка – вершиной.

Конусом называется тело, ограниченное одной полостью конической поверхности с замкнутой направляющей и плоскостью, пересекающей все образующие этой полости и не проходящей через вершину.

Часть этой плоскости, лежащая внутри конической поверхности, называется основанием конуса.

Высота конуса – это перпендикуляр, опущенный из вершины конуса на плоскость основания.

Часть конической поверхности, расположенная между вершиной и плоскостью основания, называется боковой поверхностью конуса.

Конус называется прямым круговым, если его направляющая – окружность, а вершина ортогонально проектируется в его центр.

Прямой круговой конус можно получить вращением прямоугольного треугольника вокруг одного из его катетов. При этом вращении другой катет опишет основание конуса, а гипотенуза – боковую поверхность.

Осью прямого кругового конуса называется прямая, содержащая его высоту.

Боковая поверхность прямого кругового конуса равна произведению половины длины окружности основания на образующую: Sбок = πRl.

Полная поверхность прямого кругового конуса вычисляется по формуле:

Sп = Sбок + Sосн= πR(l + R).

 Объем прямого кругового конуса вычисляется по формуле: V = (πR²H)/3

Шар

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не больше данного, от данной точки. Эта точка называется центром шара (на рисунке – это точка О), а данное расстояние (на рисунке – R) – радиусом шара. Шар получается при вращении полукруга вокруг его диаметра как оси.

Г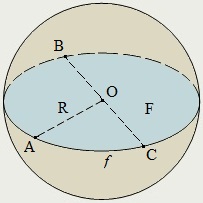 раница шара называется шаровой поверхностью или сферой. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок (ОА), соединяющий центр шара с точкой шаровой поверхности, также называется радиусом.Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром (ВС). Концы любого диаметра называются диаметрально противоположными точками шара (точки В и С).

Площадь сферы и объём шара можно найти по формулам:

S = 4πR²= πD²;

V = (4πR³)/3 = (πD³)/6,

где R – радиус, D – диаметр сферы и шар

Приложение 2