Интерактивная презентация по теме "Системы счисления"

Основные понятия

Система счисления

- это способ записи чисел и правила действий над этими числами

Число

- это величина, а не символьная запись

Цифра

- набор символов, участвующих в записи числа

Алфавит

- совокупность различных цифр, используемых для записи числа

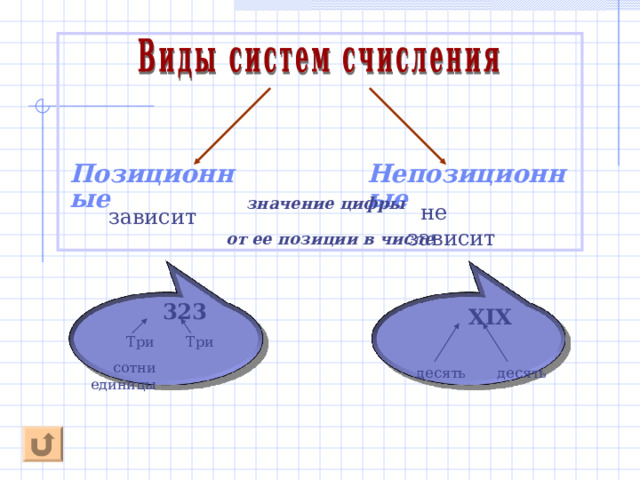
Позиционные

Непозиционные

значение цифры

не зависит

зависит

от ее позиции в числе

323

Три Три

сотни единицы

XIX

десять десять

Непозиционные системы счисления

• единичная

• древнеегипетская

• вавилонская
• римская

• алфавитная

I,V,X,L,C,D,M

колода

Единичная («палочная система»)

(период палеолита, 10-11 тысяч лет до н.э.)

Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе.

Обозначение :

или

Древнеегипетская система

(ок.2850 до н.э.)

Иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления.

Обозначение :

- сотни

- десятки

- единицы

= 3 4 5

Вавилонская шестидесятеричная система (2 тысячи лет до н.э.)

Первая известная нам система счисления, основанная на позиционном принципе .

Обозначение :

- десятки

- единицы

; 60 2

- 60

; 60 3

; … ; 60 n

= 60 +20+2 = 82

1-ый

разряд

2-ой

разряд

Римская система

(500 лет до н.э.)

В качестве цифр в римской системе используются:

M

V

I

X

L

C

D

50

1

5

10

100

500

1000

Величина числа суммируется из значений цифр. При этом применяется следующее правило:

Значение каждой меньшей цифры, поставленной слева от большей, вычитается из значения большей цифры. Если меньшая цифра стоит справа от большей, их значения складываются.

Найдите значения чисел:

= 3 2

= 542

D X L I I

X X X I I

Алфавитные системы

(500 лет до н.э.)

Алфавитной нумерацией пользовались южные и восточные славянские народы. Над буквой, обозначавшей цифру, ставился специальные значок "~" ( «титло»).

Обозначение:

1 2 3 4 5 6 7 8 9 10

Позиционные системы счисления

Каждая позиционная система счисления имеет определенный алфавит и основание.

– основание ( p)

Количество цифр

системы счисления

Совокупность всех цифр

– алфавит

Позиционные системы могут иметь различный алфавит (2,3,4 знака).

10 к десяти арабским цифрам добавляют латинские буквы. Алфавиты систем счисления Основание р = 2 Название Алфавит Двоичная р = 3 р = 8 0 1 Троичная р = 16 Восьмеричная 0 1 2 0 1 2 3 4 5 6 7 Шестнадцатеричная 0 1 2 3 4 5 6 7 8 9 A B C D E F " width="640"

Позиция цифры в числе называется разрядом .

Для записи чисел в позиционной системе с основанием р нужно иметь алфавит из р цифр. При р 10 к десяти арабским цифрам добавляют латинские буквы.

Алфавиты систем счисления

Основание

р = 2

Название

Алфавит

Двоичная

р = 3

р = 8

0 1

Троичная

р = 16

Восьмеричная

0 1 2

0 1 2 3 4 5 6 7

Шестнадцатеричная

0 1 2 3 4 5 6 7 8 9 A B C D E F

ПРИМЕРЫ : (перепиши, вставляя пропущенные числа)

• p = 10 ( десятичная с /c )

1 2 3 4 5 6 7 8 9 10 11 12 13 14 и т.д.

• p = 4 ( четверичная с /c )

1 2 3 10 11 12 13 20 21 22 23 30 __ __ __ __

3. p = 2 ( двоичная с /c )

1 10 11 100 101 110 111 1000 ___ 1010 1011 ____ ___ ___ ___ 10000 _____ _____

4. p = 16 ( шестнадцатеричная с /c )

1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B ___ _ __ __ _ __ _

31 32 33 1 0 0

1001

1100

1101

1110

1111

10001

10010

1 C 1D 1E 1F

Вопрос для обсуждения

В наше время для записи чисел чаще всего используются две системы счисления:

- арабская десятичная (цифры 0,1,2,3,4,5,6,7,8,9 )

- римская (цифры I,V,X,L,C,M )

1.Где сегодня используется римская система счисления для записи чисел?

Рассмотрим 2 числа: XXX и 333 .

2.Чем отличается принцип записи многозначных чисел в римской и арабской системах счисления?

Десятичная система счисления

Получив название арабской эта система счисления, в XII веке распространилась по всей Европе.

Система счисления, применяемая в современной математике, является позиционной десятичной системой .

Её основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9 - алфавит .

Рассмотрим десятичное число 555 :

Число записано в привычной для нас свернутой форме :

В зависимости от позиции цифра 5 обозначает единицы, десятки, сотни.

5 5 5 10

единицы

десятки

сотни

Из двух написанных рядом одинаковых цифр левая в десять раз больше правой.

В развернутой форме записи числа умножение цифр производится в явной форме:

Любое число в нулевой степени равно 1

555 10 = 5 · 10 2 + 5 · 10 1 + 5 · 10 0

Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания :

Любое число в отрицательной степени = единица / число в положительной степени: 10 -1 =1 / 10 1 , 10 - 2 = 1/ 10 2

555,55 10 = 5 · 10 2 + 5 · 10 1 + 5 · 10 0 + 5 · 10 -1 + 5 · 10 -2

2 1 0 -1 -2

Степень основания

Первый разряд цифры, стоящей слева от запятой равен 0

Основание системы счисления

Номер разряда стоящей в нем цифры равен значению степени основания

Вопрос для обсуждения

1) В какой системе счисления удобнее считать?

2) Почему арабская система называется десятичной?

Двоичная система счисления

Информация в компьютере представлена в двоичном коде. Используется двоичная система счисления.

Двоичная система счисления является позиционной системой счисления .

Алфавит двоичной системы – две цифры (0,1), основание равно 2.

Из двух написанных рядом одинаковых цифр левая в два раза больше правой.

Число в свернутой форме записывается так:

101,01 2

В развернутой форме число записывается в виде суммы ряда степеней основания 2 с коэффициентами, в качестве цифр 0 или1.

101,01 2 = 1 · 2 2 + 0 · 2 1 + 1 · 2 0 + 0 · 2 -1 + 1 · 2 -2

= 5,25 10

2 1 0 -1 -2

Степень основания

Первый разряд цифры, стоящей слева от запятой равен 0

Вычислив значение суммы, получаем число в десятичной системе счисления

Основание системы счисления

Номер разряда стоящей в нем цифры равен значению степени основания

Восьмеричная система счисления

Широко используется в информатике.

Восьмеричная система счисления является позиционной системой счисления .

Алфавит восьмеричной системы – цифры (0,1,2,3,4,5,6,7), основание равно 8.

Из двух написанных рядом одинаковых цифр левая в восемь раз больше правой.

Число в свернутой форме записывается так:

137,2 8

В развернутой форме число записывается в виде суммы ряда степеней основания 8 с коэффициентами, в качестве цифр от 0 до 7.

137,2 8 = 1 · 8 2 + 3 · 8 1 + 7 · 8 0 + 2 · 8 -1

= 95,25 10

2 1 0 -1

Степень основания

Первый разряд цифры, стоящей слева от запятой равен 0

Вычислив значение суммы, получаем число в десятичной системе счисления

Основание системы счисления

Номер разряда стоящей в нем цифры равен значению степени основания

Шестнадцатеричная система счисления

Широко используется в информатике .

Шестнадцатеричная система счисления является позиционной системой счисления .

Алфавит шестнадцатеричной системы – цифры (0,1,2,3,4,5,6,7,8,9, A,B,C,D,E,F ), основание равно 16.

(Десятичное значение: A=10, B=11, C=12, D=13, E=14, F=15 )

Из двух написанных рядом одинаковых цифр левая в шестнадцать раз больше правой.

Число в свернутой форме записывается так:

12 A ,4 16

В развернутой форме число записывается в виде суммы ряда степеней основания 16 с коэффициентами, в качестве цифр от 0 до F , выражая шестнадцатеричные цифры через их десятичное значение ( A=10, F=15).

12 A ,4 16 = 1 ·16 2 + 2 ·16 1 + 10·16 0 + 4 ·16 -1

= 298,25 10

2 1 0 -1

Степень основания

Первый разряд цифры, стоящей слева от запятой равен 0

Вычислив значение суммы, получаем число в десятичной системе счисления

Основание системы счисления

Номер разряда стоящей в нем цифры равен значению степени основания

Алгоритм перевода чисел,

записанных в произвольной системе счисления,

в десятичную систему счисления

1. Записать число в развернутой форме в виде сумм ряда степеней основания системы счисления с коэффициентами в качестве цифр данной системы счисления.

2 . Вычислить полученную сумму .

231,2 4 = 2 · 4 2 + 3 · 4 1 + 1 · 4 0 + 2 · 4 -1

= 45,5 10

2 1 0 -1

Переведи в десятичную сс:

Степень основания = номер разряда цифры

112 3 =

1 · 3 2 + 1 · 3 1 + 2 · 3 0 = 14 10

Основание системы счисления

134 6 =

1 · 6 2 + 3 · 6 1 + 4 · 6 0 = 58 10

Задания для самостоятельного выполнения

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Какое минимальное основание должна иметь система счисления, если в ней можно записать числа:

а) 341

б) 123

в) 222

г) 111

Ответ: а) 341 (р=5) в) 222 (р=3)

б) 123 (р=4) г) 111 (р=2)

Какое число ошибочно записано в:

а) троичной СС – 79, 212, 531

б) девятеричной СС – 419, 832, 4А

• а) троичной СС – 79, 212, 531 б) девятеричной СС – 419, 832, 4А

Ответ: а) в троичной СС для записи чисел используются цифры 0 1 2 , значит цифры 79 и 531 записаны неверно

б) в девятиричной СС для записи чисел используются цифры 0 1 2 3 4 5 6 7 8, значит цифры 419 и 4А записаны неверно

Какое максимальное число можно записать в двоичной системе счисления четырьмя цифрами?

Переведите полученное число в десятичную систему счисления.

Ответ: 1111 2 = 15 10 .

Определите четное число или нечетное:

а) 101 2

б) 110 2

в) 1001 2

г) 100 2

Сформулируйте критерий четности в двоичной системе счисления.

Ответ: четное число в двоичной системе счисления оканчивается на 0, а нечетное – на 1.

а) 101 2 = 5 10 б) 110 2 = 6 10

в) 1001 2 = 9 10 г) 100 2 = 4 10

Было 11 яблок. После того как каждое яблоко разрезали пополам, стало 110 половинок.

Возможно ли это? Обоснуйте ответ.

Ответ: да , если считать числа в задаче, представленными в двоичной системе счисления:

1 1 2 = 1  2 1 + 1  2 0 = 3 10 ;

1 1 0 2 = 1  2 2 + 1  2 1 + 0  2 0 = 4 + 2 = 6 10

Выпишите алфавит традиционной позиционной пятеричной системы счисления.

Переведите число 32 5 в десятичную систему счисления.

Ответ: алфавит пятеричной системы счисления – цифры (0,1,2,3,4).

32 5 = 3  5 1 + 2  5 0 = 15 + 2 = 17 10

« Мысль – выражать все числа немногими знаками, придавая им не только значение по форме, но еще и значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна …»

Пьер Симон Лаплас

(1 7 49 – 18 27 гг.)

Система счисления - это совокупность приемов и правил записи чисел с помощью определенного набора символов (некоторый способ кодирования числовой информации).

Системы счисления

непозиционные

позиционные

Цифры – знаки которые используются для записи чисел

История развития систем счисления

Непозиционные системы счисления

Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок):

Зарубок черточек точек

Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.

Отголоски единичной системы счисления встречаются и сегодня. Так, чтобы узнать, на каком курсе учится курсант военного училища, нужно сосчитать, какое количество полосок нашито на его рукаве.

Сами того не осознавая,  единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, а счетные палочки используется для обучения учеников 1-го класса счету

Единичная система — не самый удобный способ записи чисел.

Записывать таким образом большие количества утомительно, и сами записи при этом получаются очень длинными.

С течением времени возникли иные, более удобные, системы счисления.

Древнеегипетская десятичная непозиционная система счисления. Примерно  в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.

Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной.

Древнеегипетская нумерация

Алфавитные системы счисления

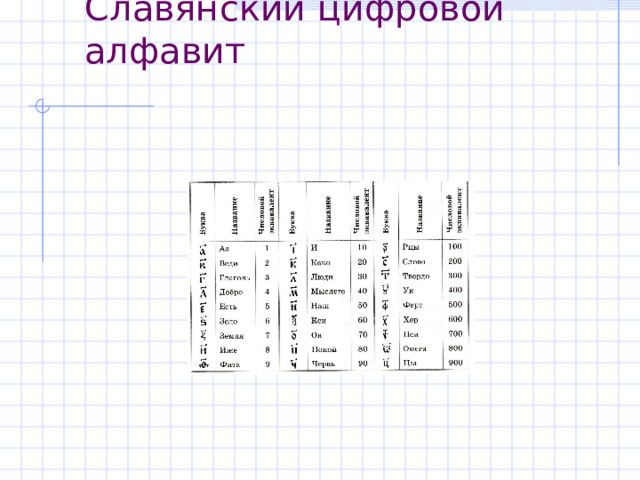
Славянский цифровой алфавит

Вавилонская система счисления

Примером непозиционной системы, которая  сохранилась  до  наших  дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем

Римскими цифрами  пользовались  очень долго.  Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами  (считалось, что обычные арабские цифры легко подделать). Римская система  счисления сегодня используется,  в основном,  для наименования знаменательных дат, томов, разделов и глав в книгах.

Римская система счисления

В римских числах цифры записываются слева направо в порядке убывания.

В таком случае их значения складываются.

Если же слева записана меньшая цифра, а справа - большая, то их значения вычитаются.

Пример :

CCXXXII=100+100+10+10+10+1+1=232 VI=5+1=6 IV=5-1=4 MCMXCVIII=

=1000+(-100+1000)+(-10+100)+5+1+1+1=1998

Позиционные системы счисления

Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.    

• В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе.
• Позиция цифры в числе называется разрядом .
• Каждая позиционная сс имеет определенный алфавит цифр и основание.

10 к десяти арабским добавляют буквы. Вот примеры алфавитов нескольких систем. " width="640"

Для записи чисел в позиционной системе с основанием п нужно иметь алфавит из п цифр. Обычно для этого при п п первых арабских цифр, а при п 10 к десяти арабским добавляют буквы. Вот примеры алфавитов нескольких систем.

А q =a n *q n +a n-1 *q n-1 +…+a 0 *q 0 +a -1 *q -1 + …+a -m *q -m

где

А q = само число

q -основание системы счисления

а – цифры данной системы счисления

п – число разрядов

Развернутая форма числа в двоичной сс :

А 2 =a n *2 n +a n-1 *2 n-1 +…+a 0 *2 0 +a -1 *2 -1 + …+a -m *2 -m

Пример: Получить развернутую форму десятичных чисел:

32478 10 =3*10 4 +2*10 3 +4*10 2 +7*10 1 + + 8*10 0

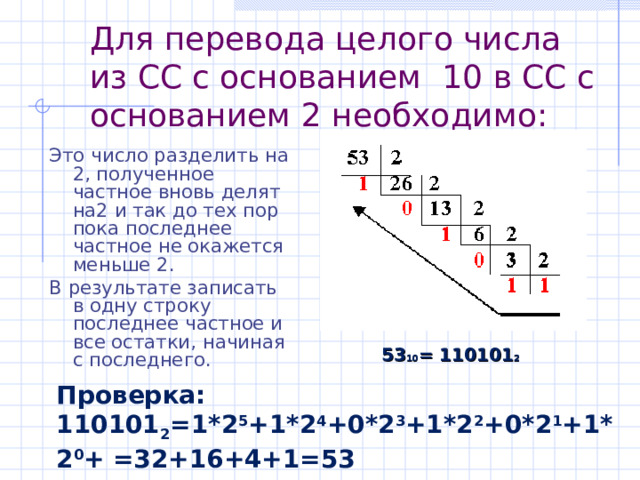
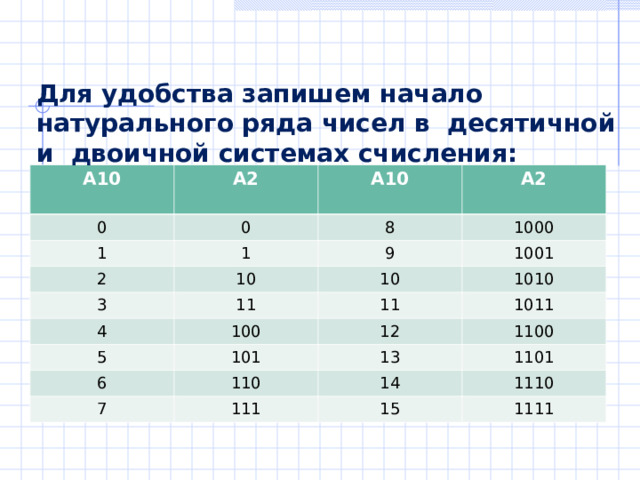
Для перевода целого числа из СС с основанием 10 в СС с основанием 2 необходимо:

Это число разделить на 2 , полученное частное вновь делят на 2 и так до тех пор пока последнее частное не окажется меньше 2 .

В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

53 10 = 110101 2

Проверка: 110101 2 =1*2 5 +1*2 4 +0*2 3 +1*2 2 +0*2 1 +1*2 0 + =32+16+4+1=53

Для удобства запишем начало натурального ряда чисел в  десятичной  и  двоичной системах счисления:

A10

0

A2

0

A10

1

A2

2

8

1

10

1000

9

3

1001

10

11

4

1010

100

5

11

12

101

6

1011

1100

110

13

7

1101

14

111

1110

15

1111

«ЛОМАЕМ» голову Прочитайте стихотворение А.Н.Старикова:

Ей было 1100 лет,

Она в 101-й класс ходила,

В портфеле по 100 книг носила -

Все это правда, а не бред.

Когда, пыля десятком ног,

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато 100-ногий .

Она ловила каждый звук

Своими 10-ю ушами,

И 10 загорелых рук

Портфель и поводок держали.

И 10 т емно-синих глаз

Рассматривали мир привычно…

Но станет все совсем обычным,

Когда поймете наш рассказ.

Занимательные задачи №2

Мартышка висит на хвосте и жует бананы. В каждой руке по 101 банану, а в каждой ноге – на 1 банан больше, чем в руке. Сколько бананов у мартышки?

Ответ в 2-й СС

Ответы к самостоятельной работе

• XXIII. X. MMX.
• 100101 2
• 1110001 2

Ключевые слова

• система счисления
• цифра
• алфавит
• позиционная система счисления
• основание
• развёрнутая форма записи числа
• свёрнутая форма записи числа
• двоичная система счисления
• восьмеричная система счисления
• шестнадцатеричная система счисления

Общие сведения

Система счисления - это знаковая система, в которой приняты определённые правила записи чисел.

Цифры - знаки, при помощи которых записываются числа.

Алфавит системы счисления - совокупность цифр.

Вавилонская система счисления

Египетская система счисления

Древнеславянская система счисления

Узловые и алгоритмические числа

Узловые числа обозначаются цифрами.

Алгоритмические числа получаются в результате каких-либо операций из узловых чисел.

 100 +

 10 +

=

Унарная система счисления

Простейшая и самая древняя система - унарная система счисления. В ней для записи любых чисел используется всего один символ - палочка, узелок, зарубка, камушек.

Узелки, дощечки

Узелковое письмо «кипу»

Примеры узлов «кипу»

Зарубки

Камушки

Непозиционная система счисления

Система счисления называется непозиционной , если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.

Римская система счисления

1

5

I

V

100

10

C

500

X

50

D

L

1000

M

Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила:

каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.

1935

M

V

I

I

I

V

X

X

28

X

X

X

M

C

X

40

L

=

Позиционная система счисления

Система счисления называется позиционной , если количественный эквивалент цифры в числе зависит от её положения в записи числа.

Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Десятичная система счисления

Цифры 1234567890 сложились в Индии около 400 г. н. э.

Арабы стали пользоваться подобной нумерацией около 800 г. н. э.

Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе.

Основная формула

В позиционной системе счисления с основанием q любое число может быть представлено в виде:

A q =±(a n–1  q n–1 + a n–2  q n–2 +…+ a 0  q 0 + a –1  q –1 +…+ a –m  q –m )

Здесь:

А — число;

q — основание системы счисления;

a i — цифры, принадлежащие алфавиту данной системы счисления;

n — количество целых разрядов числа;

m — количество дробных разрядов числа;

q i — «вес» i -го разряда.

Такая запись числа называется развёрнутой формой записи.

Развёрнутая форма

A q =±(a n–1  q n–1 + a n–2  q n–2 +…+ a 0  q 0 + a –1  q –1 +…+ a –m  q –m )

Примеры записи чисел в развёрнутой форме:

2012=2  10 3 +0  10 2 +1  10 1 +2  10 0

0,125=1  10 -1 +2  10 -2 +5  10 –3

14351,1=1  10 4 +4  10 3 +3  10 2 +5  10 1 +1  10 0 +1  10 –1

Двоичная система счисления

Двоичной системой счисления называется позиционная система счисления с основанием 2 .

Двоичный алфавит : 0 и 1.

Для целых двоичных чисел можно записать:

a n–1 a n–2 …a 1 a 0 = a n–1  2 n–1 + a n–2  2 n–2 +…+ a 0  2 0

Например:

10011 2 =1  2 4 +0  2 3 +0  2 2 +1  2 1 +1  2 0 = 2 4 +2 1 + 2 0 =19 10

Правило перевода двоичных чисел в десятичную систему счисления:

Вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа

Правило перевода целых десятичных чисел в двоичную систему счисления

a n–1  2 n–1 +a n–2  2 n–2 +… a 1  2 1 +a 0

= a n–1  2 n–2 +…+ a 1 (остаток a 0 )

2

a n–1  2 n–1 +a n–2  2 n–2 +… a 1

= a n–1  2 n–3 +…+ a 2 (остаток a 1 )

2

a n–1  2 n–1 +a n–2  2 n–2 +… a 2

= a n–1  2 n–4 +…+ a 3 (остаток a 2 )

2

. . .

На n -м шаге получим набор цифр: a 0 a 1 a 2 …a n–1

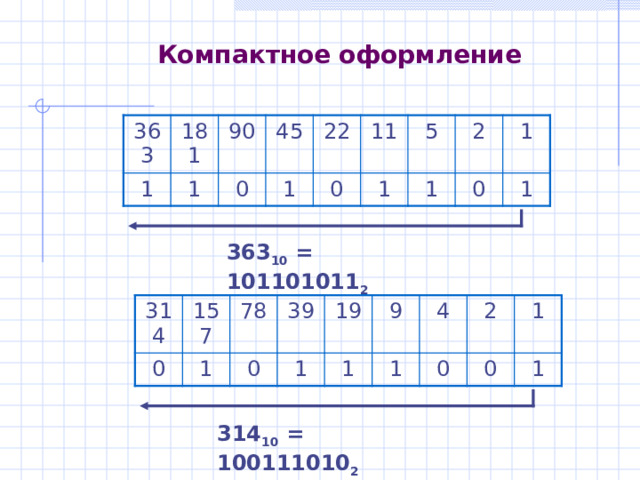
Компактное оформление

363

181

1

90

1

45

0

1

22

11

0

5

1

2

1

0

1

1

363 10 = 101101011 2

314

0

157

78

1

39

0

1

19

1

9

1

4

0

2

1

0

1

314 10 = 100111010 2

Восьмеричная система счисления

Восьмеричной системой счисления называется позиционная система счисления с основанием 8.

Алфавит: 0, 1, 2, 3, 4, 5, 6, 7.

a n–1 a n–2 …a 1 a 0 = a n–1  8 n–1 +a n–2  8 n–2 +…+a 0  8 0

Пример: 1063 8 =1  8 3 +0  8 2 +6  8 1 +3  8 0 =563 10 .

Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.

Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.

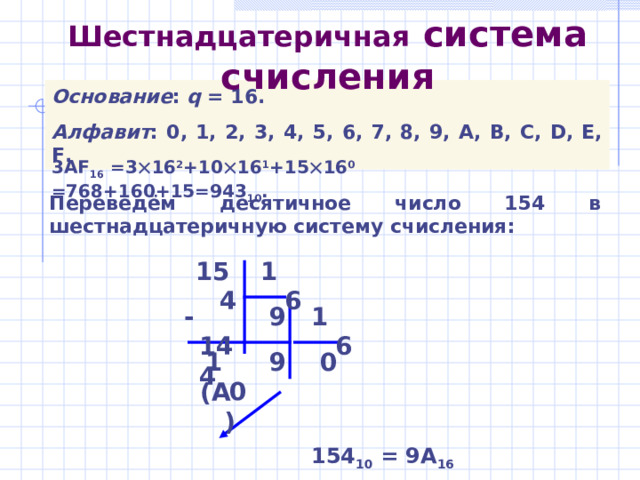
Шестнадцатеричная система счисления

Основание : q = 16.

Алфавит : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

3АF 16 =3  16 2 +10  16 1 +15  16 0 =768+160+15=943 10 .

Переведём десятичное число 154 в шестнадцатеричную систему счисления:

154

16

9

-144

16

10

9

0

(А)

154 10 = 9А 16

Правило перевода целых десятичных чисел в систему счисления с основанием q

1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;

2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;

3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.

Цифровые весы

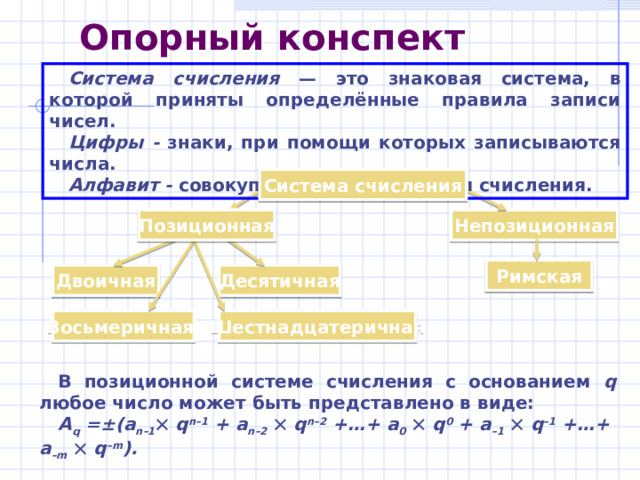
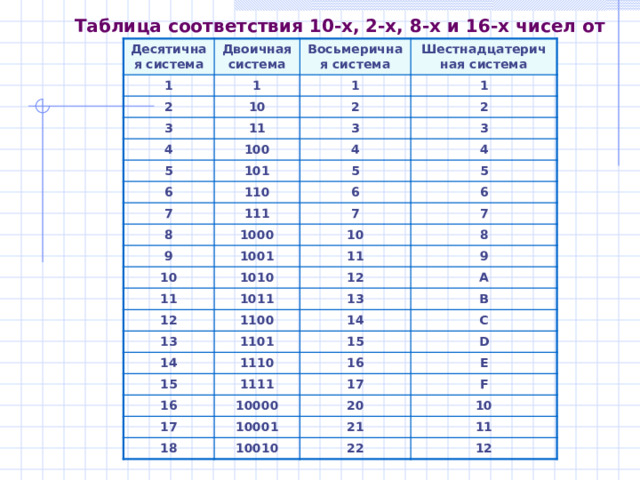
Таблица соответствия 10-х, 2-х, 8-х и 16-х чисел от 1 до 16

Десятичная система

Двоичная система

1

Восьмеричная система

1

2

Шестнадцатеричная система

1

10

3

4

1

2

11

5

100

3

2

3

6

4

101

5

4

7

110

5

6

111

8

9

6

7

1000

10

1001

7

10

8

11

1010

11

9

12

1011

12

A

13

13

1100

1101

14

14

B

C

15

15

1110

1111

16

16

D

E

17

10000

17

F

20

10001

18

10

21

10010

11

22

12

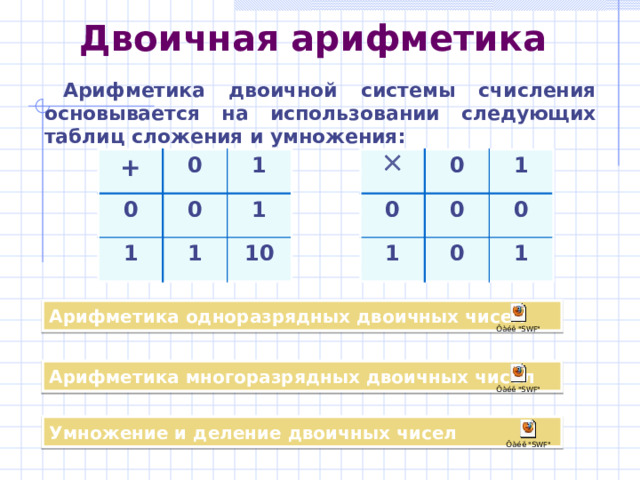
Двоичная арифметика

Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:



+

0

0

0

0

1

0

1

1

0

1

1

0

1

0

10

1

Арифметика одноразрядных двоичных чисел

Арифметика многоразрядных двоичных чисел

Умножение и деление двоичных чисел

«Компьютерные» системы счисления

Двоичная система используется в компьютерной технике, так как:

• двоичные числа представляются в компьютере с помощью простых технических элементов с двумя устойчивыми состояниями;
• представление информации посредством только двух состояний надёжно и помехоустойчиво;
• двоичная арифметика наиболее проста;
• существует математический аппарат, обеспечивающий логические преобразования двоичных данных.

Двоичный код удобен для компьютера.

Человеку неудобно пользоваться длинными и однородными кодами. Специалисты заменяют двоичные коды на величины в восьмеричной или шестнадцатеричной системах счисления.

Самое главное

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел.

Система счисления называется позиционной , если количественный эквивалент цифры в числе зависит от её положения в записи числа.

В позиционной системе счисления с основанием q любое число может быть представлено в виде:

A q =±(a n–1  q n–1 + a n–2  q n–2 +…+ a 0  q 0 + a –1  q –1 +…+ a –m  q –m )

Здесь:

А — число;

q — основание системы счисления;

a i — цифры, принадлежащие алфавиту данной системы счисления;

n — количество целых разрядов числа;

m — количество дробных разрядов числа;

q i — «вес» i -го разряда.

Вопросы и задания

Переведите целые числа из десятичной системы счисления в восьмеричную:

а) 513

б) 600

в) 2010

Выполните операцию умножения над двоичными числами:

а) 1010 · 11

б) 111 · 101

в) 1010 · 111

Запишите десятичные эквиваленты следующих чисел:

а) 172 8

б) 2ЕА 16

в) 101010 2

г) 10,1 2

д) 243 6

Переведите целые числа из десятичной системы счисления в двоичную:

а) 89

б) 600

в) 2010

Переведите целые числа из десятичной системы счисления в шестнадцатеричную:

а) 513

б) 600

в) 2010

Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.

Запишите в развёрнутом виде числа:

а) 143,511 10

б) 143511 8

в) 143511 16

г) 1435,11 8

Укажите, какое из чисел 110011 2 , 111 4 ,35 8 и1В 16 является:

а) наибольшим

б) наименьшим

Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?

Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе:

а) 1100 ? 11 ? 100 = 100000;

б) 1100 ? 10 ? 10 = 100;

в) 1100 ? 11 ? 100 = 0.

Найдите основание х системы счисления, если:

а) 14 x =9 10

б) 2002 x =130 10

Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.

Цифры каких систем счисления приведены на рисунке?

Чем различаются унарные, позиционные и непозиционные системы счисления?

Выполните операцию сложения над двоичными числами:

а) 101010 + 1101

б) 1010 + 1010

в) 10101 + 111

Вычислите выражения:

а) (1111101 2 +AF 16 ):36 8

б) 125 8 + 101 2 ·2A 16 – 141 8

Ответ дайте в десятичной системе счисления.

Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.

Верны ли следующие равенства?

а) 33 4 =21 7

б) 33 8 =21 4

Основание 2

Основание 8

101010

Основание 10

Основание 16

127

321

2А

Задачник «Системы счисления»

Опорный конспект

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел.

Цифры - знаки, при помощи которых записываются числа.

Алфавит - совокупность цифр системы счисления.

Система счисления

Непозиционная

Позиционная

Римская

Десятичная

Двоичная

Шестнадцатеричная

Восьмеричная

В позиционной системе счисления с основанием q любое число может быть представлено в виде:

A q =±(a n–1  q n–1 + a n–2  q n–2 +…+ a 0  q 0 + a –1  q –1 +…+ a –m  q –m ).