«Интересный свойства трапеции»

Проект по геометрии на тему:

«Интересный свойства трапеции»

С О Д Е Р Ж А Н И Е:

• Что такое трапеция?

• Виды трапеций

• Свойства трапеции

Цель:

«улучшить и закрепить свои знание о геометрической фигуре-трапеции»

Что представляет собой Трапеция?

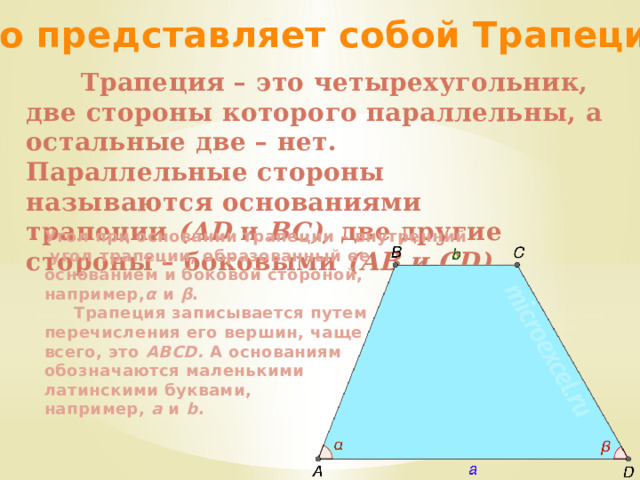
Трапеция – это четырехугольник, две стороны которого параллельны, а остальные две – нет.

Параллельные стороны называются основаниями трапеции  (AD  и  BC) , две другие стороны – боковыми  (AB и CD) .

Угол при основании трапеции – внутренний

угол трапеции, образованный ее

основанием и боковой стороной,

например, α  и  β .

Трапеция записывается путем

перечисления его вершин, чаще

всего, это  ABCD.  А основаниям

обозначаются маленькими

латинскими буквами,

например,  a  и  b .

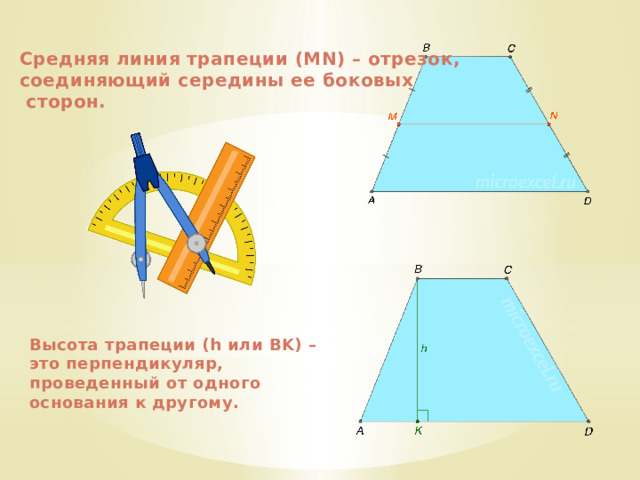
Средняя линия трапеции (MN) – отрезок,

соединяющий середины ее боковых

сторон.

Высота трапеции (h или BK) – это перпендикуляр, проведенный от одного основания к другому.

Виды трапеций

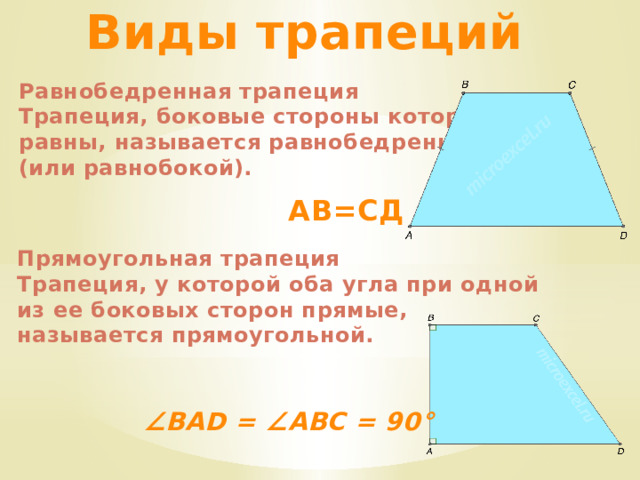
Равнобедренная трапеция

Трапеция, боковые стороны которой равны, называется равнобедренной

(или равнобокой).

АВ=СД

Прямоугольная трапеция

Трапеция, у которой оба угла при одной из ее боковых сторон прямые, называется прямоугольной.

∠ BAD = ∠ABC = 90°

Свойства трапеции

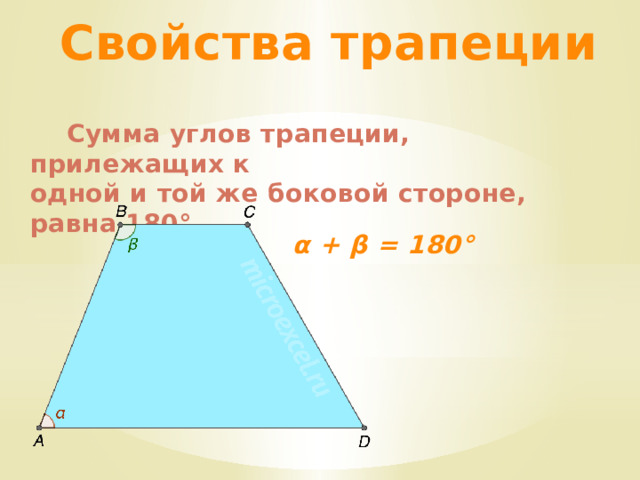
Сумма углов трапеции, прилежащих к

одной и той же боковой стороне, равна 180°.

α + β = 180°

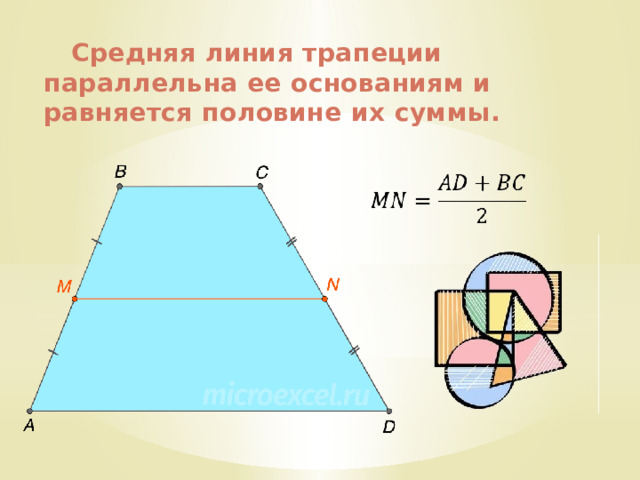
Средняя линия трапеции параллельна ее основаниям и равняется половине их суммы.

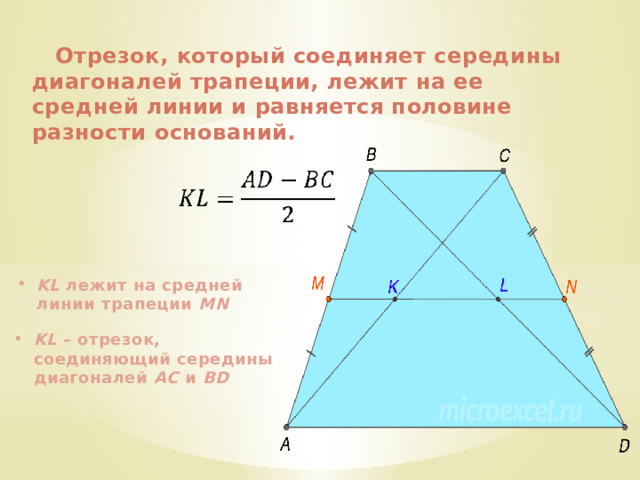
Отрезок, который соединяет середины диагоналей трапеции, лежит на ее средней линии и равняется половине разности оснований.

• KL  лежит на средней линии трапеции  MN

• KL  – отрезок, соединяющий середины диагоналей  AC  и  BD

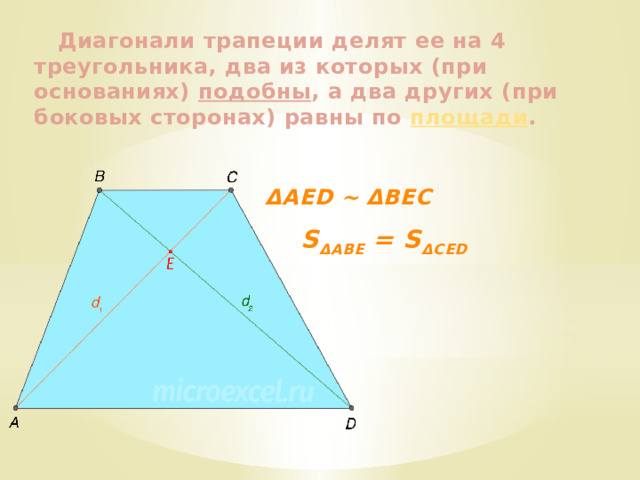
Диагонали трапеции делят ее на 4 треугольника, два из которых (при основаниях)  подобны , а два других (при боковых сторонах) равны по  площади .

ΔAED ~ ΔBEC

S ΔABE  = S ΔCED

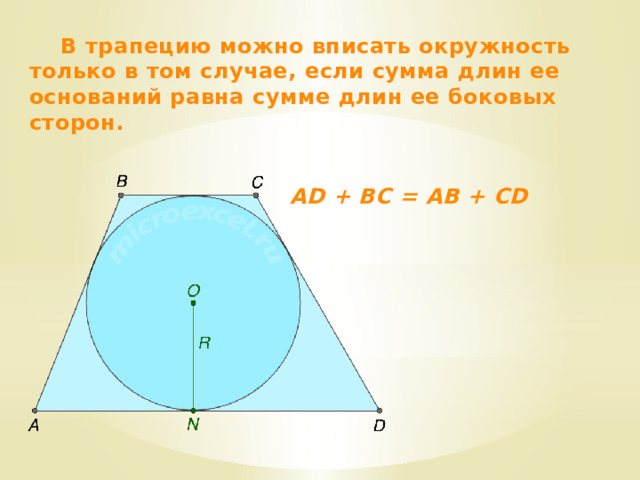
В трапецию можно вписать окружность только в том случае, если сумма длин ее оснований равна сумме длин ее боковых сторон.

  AD + BC = AB + CD

Спасибо за внимание!