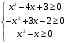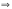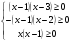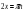Использование инструментов ТРИЗ в обучении студентов математике

2. Использование инструментов ТРИЗ в обучении студентов математике

2.1. Ситуация как средство развития творческих способностей

Математика, особенно в школе, воспринимается как «нетворческий» предмет. О развитии творческих математических способностей на занятиях математики можно прочитать в книгах Д. Пойа, Н. Тучнина и прочих. Однако речь в них идет именно о математическом творчестве, а сегодняшний социальный заказ общества требует от человека, среди других качеств, умение действовать в нестандартных ситуациях, причем далеких от применения «явной» математики. Таким образом, речь идет о формировании такого качества личности, как креативность, а не математическая креативность.

При решении текстовых задач рекомендуется от задачи переходить к модели задачи, таким образом, дальнейшее решение заключается в решении модели

Сформулируем ИКР (идеальный конечный результат): система осталась неизменной, но требование стало выполняться. Используем инструмент ТРИЗ - вепольный анализ, который позволяет добавить в систему новое «вещество» Х, которое создает поле, соответствующее предложенному требованию

Тогда, используя общий алгоритм решения задачи в ТРИЗ, элемент Х - это некоторая ситуация

Именно переход от ситуации к задаче должен помочь развивать на занятиях математики креативность, причем при использовании этой схемы отработанная методика по использованию модели перехода от задачи просто необходима для сохранения других дидактических целей.

Задача отличается от ситуации наличием четкой формулировки, условие содержит все необходимые данные в явном виде, метод решения часто известный и является цепочкой формальных операций, правильный ответ определен однозначно. Ситуация в свою очередь имеет неопределенное условие, разные подходы к решению, множество решений, благодаря чему она ближе к проблемным ситуациям, возникающим в жизни.

Основная цель практико-ориентированных (прикладных и практических) задач на занятиях математики заключается в осуществлении содержательной и методологической связи школьного курса математики с профессиональной составляющей образования, то есть способствует развитию профессиональных умений, входящих в состав учебной и познавательной деятельности в процессе изучения математики, а не развития креативности студента. Поэтому практико-ориентированные задачи нельзя в полной мере назвать ситуацией.

Пример 1. Окно имеет форму прямоугольника, завершенного сверху полукругом. Укажите такие размеры окна с периметром Р, чтобы при этом оно пропускало больше света.

Этот пример - практически-ориентированного задания, и его решение заключается в применении производной (задача на максимум и минимум). Четкая формулировка условия задачи, все необходимые данные в явном виде, метод решения представляет собой цепочку формальных операций. Поэтому это задача, а не ситуация.

2.2. Мета-алгоритм изобретения ТРИЗ

и решения учебных математических задач

ТРИЗ является качественной теорией. Строгое соответствие моделей качественных теорий концепциям конструктивной математики очень упрощена; можно сказать, что конструктивная математика имеет дело с качественными моделями, определяемыми следующим конструктивным способом: 1) фиксируются начальные конструктивные объекты, определенные, в частности, в виде примеров или образцов; 2) фиксируются правила (не обязательно аксиоматические), по которым строятся новые объекты из уже имеющихся; 3) фиксируются условия, накладываемые на начальные и построенные объекты и определяется их конструктивность (например, осуществимость, полезность и эффективность).

Совокупность правил, определяющих построение новых конструкций, называется алгоритмом. Обобщенные алгоритмы, на основе которых могут быть построены специализированные (ориентированные на определенное применение к определенному классу моделей) или детализированные (точные) алгоритмы в ТРИЗ называются мета-алгоритмами. Поэтому логично рассмотреть применение мета-алгоритма ТРИЗ в преподавании.

Рассмотрим обобщенную схему мета-алгоритма изобретения, а также упрощенный мета-алгоритм для решения некоторого класса учебных математических задач.

Тогда ход решения задачи можно разложить на 4 больших этапа:

- диагностика (исследование задачи)

- редукция (построение модели задачи)

- трансформация (выбор метода решения (вычисления) модели)

- верификация (проверка решения).

1 3

Рис. 5

При этом эта схема совпадает с методикой организации решения учебной математической задачи соблюдением формально-логической схемы рассуждения «анализ - построение - доказательство - исследование» при решении геометрических задач на построение и тому подобное.

Переходы 1 и 3 требуют знания теории моделей и прикладных сфер ее применения. Переход 2 требует умения строить и решать модели теории.

Пример 2. Чем больше или? Решение представлено на рисунке 6.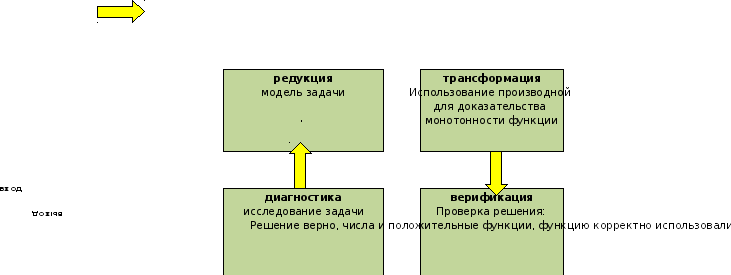

2

1 3

Рис. 6

Необходимо сравнить два числа. На этапе диагностики проблемы было установлено, что непосредственное сравнение сложное. На этапе редукции была построена функция (обобщение по двум ее значениями). На этапе трансформации из методов доказательства монотонности функции выбрали наиболее подходящий с использованием производной. На этапе верификации доказали монотонность.

На этапе верификации путем исследования полученного решения убедились в правильности решения задачи.

Таким образом, при использовании мета-алгоритма для решения учебных математических задач появляется возможность наглядно представлять ход решения задачи.

Причем на этапах диагностики и редукции преимущественно используется анализ (проблемы решения), на этапах трансформации и верификации - синтез (идеи решения). Тем самым, используя при решении задачи мета-алгоритм, студенты на занятиях по математике осознанно учатся использовать различные способы мышления.

2.3. Метод переизобретения знаний

ТРИЗ является продолжением диалектики Аристотеля и Гегеля и дополняет их конкретными инструментальными методами преодоления противоречий. Поэтому ТРИЗ позволяет более описывать, а главное - проектировать процессы развития различных систем. Таким образом, изучая любую систему, можно более глубоко понять эту систему и одновременно формировать творческое мышление, если рассматривать ее как результат развития системы-предшественника, преодоления в ней противоречий в соответствии с теми закономерностей, которые теперь известны, как законы, принципы, приемы , стандарты ТРИЗ. Один из вариантов такого рассмотрения - переизобретение знаний при помощи ТРИЗ.

Объектами изучения в математике являются глубинные закономерности нашего мира, выраженные в математических понятиях и правилах. И те, и другие, согласно ТРИЗ, а также философским наукам системологии и диалектике, являются системами развивающимися. Рассмотрим возможности их переизобретения в учебном процессе.

При использовании элементов ТРИЗ-педагогики при изучении математики и курса путем переизобретения знаний вполне возможно переизобретать НЕ закономерности, а понятия, описывающие их, и правила.

Пример 3. Когда людям были известны только целые числа. Но оказывалось недостаточно, в частности, когда было необходимо измерять доли каких-либо объектов. В результате стихийного применения принципа дробления люди создали идею дробей. Развитие дробных чисел можно рассматривать и дальше. Первые дроби у древних (унция и т.п.) Были очень неудобными, особенно в арифметических операциях. Проблема была решена с использованием для записи дробных чисел их предшественников - целых чисел - стихийным применением закона перехода к бисистеме. Современная простая дробь - это бисистема из числителя и знаменателя. Смешанные числа - это полисистемы из целой части, числителя и знаменателя. Проблема сложения и вычитания простых дробей с разными знаменателями была решена путем стихийного применения принципа эквипотенциальности (приведения к общему знаменателю). Все же в обыкновенных дробях правила выполнения арифметических операций, хотя и достаточно понятны, но не совсем просты, отличаются от правил операций с целыми числами. Проблема была решена стихийным применением к целым числам принципа инверсии. В десятичных дробях вес разрядов справа от запятой - отрицательная, в противоположность положительному весу разрядов слева от запятой.

Пример 4. Отрицательные числа получаются из положительных путем применения принципа инверсии.

Пример 5. Иррациональные числа получаются из рациональных путем применения принципа непрерывности полезного действия: числа занимают непрерывно всю числовую ось.

Пример 6. Комплексные числа получаются из действительных (вещественных) путем применения принципа перехода в другое измерение: от числовой прямой к числовой комплексной плоскости.

Пример 7. Переменные получаются из констант путем применения принципа динамичности.

Пример 8. Функции одной переменной получаются из одиночных переменных по закону перехода к бисистеме.

Пример 9. Функции нескольких переменных получаются из функций одной переменной по закону перехода к полисистеме.

Пример 10. Создание Ньютоном и Лейбницем интегрального исчисления - классический пример перехода на микроуровень.

Таким образом, можно аналогично рассуждать относительно других математических объектов, используя метод переизобретения знаний. Использовать этот метод на факультативном занятии.

2.4. Принципы решения математических задач

На основе ТРИЗ можно сформулировать советы - принципы решения математических задач, которые могут помочь избежать многих ошибок и подсказать, как найти решение.

Принцип отсроченного действия. После прочтения задачи первое желание, которое может возникнуть, не решать его. Можно пойти навстречу этому желанию, повременить с преобразованиями и другими действиями. Возможно, именно в этот момент будет заметна полезная закономерность. Если данный этап не принес плодов, необходимо попытаться найти область определения или хотя бы некоторое множество, содержащее ее.

Пример 11. Решить уравнение:.

Не надо спешить строить обе части уравнения в квадрат, а найдем область определения:

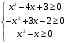
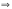
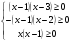
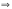
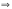
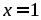
Подставляя х = 1, необходимо убедиться, что это единственный корень.

Принцип максимума локальной информации. На каждом шагу процесса поиска решения необходимо стремиться получить максимальную информацию из структуры полученной ситуации. Этот принцип был использован при решении предыдущей задачи.

Принцип правильности решения. Некоторые описки и ошибки осуществляются человеком на подсознательном уровне (иногда достаточно при решении задачи один раз заменить знак «плюс» на «минус» и дальше можно уже никуда не спешить, потому что все последующие правильные действия приведут к неправильному результату) и поэтому выявить их самому очень трудно. Отсюда вытекает необходимость как локального контроля (каждый шаг в решении проверять дважды), так и глобальной проверки (проверка результата решения, хотя бы частично, на правильность и реальность.

Пример 12. Решить уравнение:.

Сведем обе части уравнения в квадрат. имеем:

,.

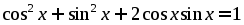
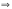
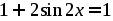
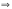
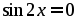
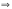
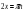
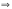
На этом решение не закончено. Было использовано возведение в квадрат, которое может привести к посторонним корням. Поэтому использовать принцип правильности решения обязательно. Тем самым после проверки получим.

Принцип отсечения ложных гипотез. В процессе решения задачи часто приводятся различного рода предположения (выдвигаются гипотезы). Главное, чего здесь следует опасаться - это не подражать ложную гипотезу.

Пример 13. Основой пирамиды является трапеция с основаниями a, b и высотой h. Грань пирамиды, проходит через меньшую основу трапеции, перпендикулярна плоскости основания. Противоположная грань является равнобедренным треугольником с углом при вершине пирамиды. Через точку пересечения диагоналей трапеции параллельно ее основаниям и вершину пирамиды проведена плоскость. Найти площадь треугольника, получившегося в сечении.

Гипотезой часто принимается, что прямая, по которой плоскость пересекает основание пирамиды, является средней линией трапеции. После этого предположения уже можно не суетиться, задача будет решена неверно.

Отсечение ложных гипотез осуществляется методом вариации параметров. Так, если в нашей задаче изменить длины боковых сторон и основание трапеции, то станет очевидно, что наша гипотеза соответствует действительности. Для отсечения ложных гипотез может пригодиться и метод от противного. Предполагаем, что гипотеза верна, и смотрим, к каким последствиям это приведет.

Принцип наихудшего случая. Если в задании говорится о пирамиде, то совсем не обязательно, чтобы она была правильной; центр вписанного в пирамиду шара не обязан лежать на высоте пирамиды и так далее.

Принцип непрерывности логических цепочек. Нельзя использовать недоказанные утверждения в процессе решения, потому недоказанное утверждение может оказаться неверным, а из неверного утверждения можно вывести истину и ложь с помощью правил рассуждения. Поэтому в логической цепочке в идеале все составляющие звенья должны присутствовать в явном виде.

Пример 14. Решить неравенство:.

Найдем область решения: .

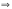
Рассмотрим начальное неравенство на интервалах:

- . Значит, в правой части начального неравенства на этом интервале стоит отрицательное выражение. Но по причине неорицательности квадратного корня. Итак, все х из этого интервала являются решениями начального неравенства.

- . Итак, на этом интервале обе части неравенства не отрицательные и допустимо возведение в квадрат.

имеем: . И далее:.

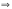
Объединяя решения из интервалов, получим ответ: .

_{Принцип полноты пространств альтернатив. Принцип утверждает необходимость исчерпывающего учета всех необходимых составных частей основания. Или все возможные случаи должны быть рассмотрены.}

_{Принцип простоты. Избранное решение поставленной задачи должно быть достаточно простым. На своем пути к познанию истины человечество стремилось к простым оригинальным и ярким решениям. С другой стороны, лишние выкладки решения, которые присутствуют в нерациональных решениях, могут служить источником дополнительных ошибок.}