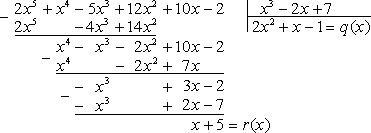Составитель: Аймжанова Агилаш Адигановна,
учитель математики
Методические рекомендации к использованию методики взаимопередачи тем при изучении математики ( из опыта работы)- Актобе, 2015.- 16с.
Рецензент: Кужакова С.Ж-заведующая кафедрой математики NIS ФМН
г. Актобе
Предисловие
Данный сборник предназначен для учителей математики и содержит в себе описание методики взаимопередачи тем, а также применение данной методики при изучении раздела «Алгебраические выражения» в 11 классе.
Использование различных методик коллективных учебных занятий, таких как: методика Ривина, методика, обратная ривинской, взаимообмен заданиями, методика взаимопередачи тем, взаимотренаж и другие, позволяют учителю разнообразнее проводить уроки, тем самым повышая интерес к предмету и личную ответственность учащихся за свое обучение.
Описание методики ВПТ
Методика взаимопередачи тем (ВПТ) предназначена для организации изучения теоретического учебного материала на основе работы учащихся в парах сменного состава.
Основная идея организации проста.
1) Ученикам необходимо освоить какой-либо раздел (блок) учебной программы. Каждый ученик должен одну или несколько тем изучить самостоятельно, а часть тем получить от других учеников. Соответственно, темы, которые он освоил самостоятельно, он должен передать своим товарищам. Самостоятельно изученные темы в обязательном порядке сдаются учителю.
Под темой понимается определённым образом оформленный текст, к которому подобраны три группы задач, упражнений, вопросов и т.д.
2)Прорабатывая текст, ученик в итоге получает подробнейший (поабзацный) план изучаемой темы и решения задач (вопросов) первой и второй групп этой темы. И только после этого тема сдаётся учителю. Учитель проверяет не только уровень освоения темы, но и готовит ученика к роли учителя, которую ему придётся выполнять при обучении другого.
3)Взаимодействие учеников организуется следующим образом. Один ученик восстанавливает другому по частям (по своему плану) содержание своей темы, после каждой части проверяет уровень понимания и задает вопросы (или предлагает решить задачи) первой группы. После этого ученик, который находится в позиции учащегося, записывает заголовок этой части. В результате совместной работы у напарника в тетради появляется подробнейший план темы. После этого ученики меняются ролями. Обучив друг друга, каждый из учеников самостоятельно приступает к выполнению упражнений второй группы. А далее они проверяют друг друга.
4) На следующем этапе ученики прорабатывают материал третьей группы.
Задания группам рекомендуется давать разного уровня.
Теории многочленов в школьном курсе математики уделено немало внимания. Учащиеся знакомятся с этими понятиями еще в 7 классе общеобразовательной программы. Наша школа работает по Интегрированной образовательной программе, где основное внимание также уделяется развитию навыков самостоятельного изучения нового материала, особенно у учащихся старших классов.
Привожу примеры использования методики ВПТ по разделу «Алгебраические выражения» в 11 классе.
Тема 1: Многочлен. Форма и описание.Действия над многочленами.
Дидактический материал
Определение1.Выражение вида 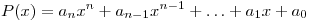 , где
, где 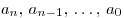 — некоторые числа и
— некоторые числа и 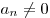 , называется многочленом степени
, называется многочленом степени 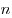 от
от 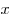 .
.
Традиционно an называется старшим коэффициентом , а a0 – свободным членом многочлена
Наивысшая степень переменной, входящих в многочлен одночленов называется степенью многочлена. Многочлен с одной переменной, старший коэффициент которого равен 1, называется приведенным.
Определение 2.Корнем многочлена с одной переменной 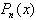 , называют те значения переменной x, при которых многочлен обращается в ноль. Иными словами, решение уравнения
, называют те значения переменной x, при которых многочлен обращается в ноль. Иными словами, решение уравнения 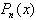 =0.
=0.
Определение3.Стандартным видом многочлена с одной переменной называется запись этого многочлена в порядке убывания степеней одночленов, каждый из которых записан в стандартном виде и среди которых нет подобных.
.
Определение 5.Два многочлена называются тождественно равными, если их числовые значения совпадают при всех значениях 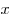 . Многочлены
. Многочлены 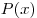 и
и 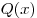 тождественно равны тогда и только тогда, когда они совпадают, т.е. коэффициенты при одинаковых степенях
тождественно равны тогда и только тогда, когда они совпадают, т.е. коэффициенты при одинаковых степенях 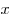 этих многочленов одинаковы.
этих многочленов одинаковы.
Определение 6.Многочленом от нескольких переменных х1 ,х2…..хn называют сумму выражений вида ….. , где а-число, k1,……kn- неотрицательные целые числа , причем буквенные части любых двух слагаемых различны.
Определение 4. Симметрический многочлен — это такой многочлен, который не изменяется при любых перестановках, входящий в него переменных.
Симметрический многочлен можно записать так: P(x, y) = P(y, x).
Например, x2y + xy2 или а+b- симметрические многочлены.
Если степени всех членов многочлена одинаковы, то этот многочлен называют однородным.
Например, x4 + 2х 3у - 6х 2у 2 + Зу 4 - однородный многочлен степени 4.
Сумма и разность многочленов
Для того, чтобы преобразовать сумму и разность многочленов в многочлен стандартного вида, надо:
1) раскрыть скобки;
2) привести подобные члены
Раскрытие скобок аналогично раскрытию скобок при действиях с числами. Если перед скобками стоит "+", слагаемые сохраняют знаки, если "-" - знаки меняются на противоположные.
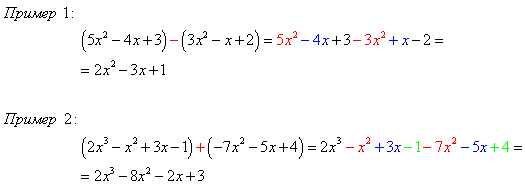
Умножение и деление многочлена на одночлен
Каждый член многочлена умножить на одночлен и полученные произведения сложить (с учетом знаков слагаемых).
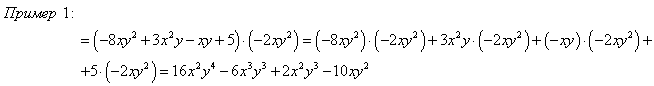
Деление многочлена на одночлен производится по аналогичному правилу.
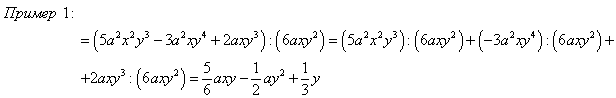
Деление многочленов
Деление многочленов выполняется "углом", если степень многочлена-делимого не меньше степени многочлена делителя.
Например,
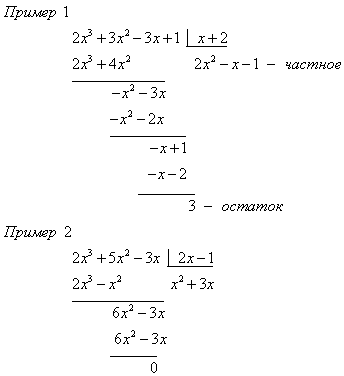
Задания группе1
1. Выбрать среди предложенных ниже алгебраических выражений те, которые являются многочленами:
;
;
.
2. Пусть f(x)=найдите и запишите в стандартном виде:
f(x) б) ( 2 f(x)2.
3. Что называют корнем многочлена?
Задания группе 2.
Заполните таблицу, считая, что f(x) и g(x) многочлены:
| Степень f(x) | Степень g(x) | Степень f(x) + g(x) | Степень f(x) g(x) | Степень f(x)3 |
| 5 | 3 |
|
|
|
|
| 7 |
|
| 21 |
|
| 4 |
| 7 |
|
|
|
| 2 |
| 9 |
|
|
| 4 | 14 |
|
Найдите все значения a и b, при которых многочлены p(x) и q(x)тождественно равны: p(x)=2ax-(a+b), q(x)=4x+(3a-b-8).
Определите степень, старший коэффициент и свободный член многочлена: –x+1)17+(11.
Задания группе 3
1. Докажите,что сумма всех коэффициентов многочлена равна f(1).
2. Докажите, что свободный член многочлена равен значению этого многочлена в точке х=0.
3. Докажите, что сумма коэффициентов членов, стоящих на четных местах равна .
Тема 2:Разложение многочлена на множители. Метод неопределенных коэффициентов
Дидактический материал
Тождественное преобразование, приводящее к произведению нескольких множителей - многочленов или одночленов, называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей
Пример. Разложить многочлен на множители 12 y 3 – 20 y 2.
Решение.
Имеем: 12 y 3 – 20 y 2 = 4 y 2 · 3 y – 4 y 2 · 5 = 4 y 2 (3 y – 5). Ответ. 4 y 2(3 y – 5).
Пример. Разложить на множители многочлен x 4 – 1.
Решение.
Имеем: x 4 – 1 = ( x 2 ) 2 – 1 2 = ( x 2 – 1)( x 2 + 1) = ( x 2 – 1 2 )( x 2 + 1) = ( x + 1)( x – 1)( x 2 + 1).Ответ. ( x + 1)( x – 1)( x 2 + 1).
Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.
Пример. Разложить на множители многочлен x 3 – 3 x 2 y – 4 xy + 12 y 2.
Решение. Сгруппируем слагаемые следующим образом:
x 3 – 3 x 2 y – 4 xy + 12 y 2 = ( x 3 – 3 x 2 y ) – (4 xy – 12 y 2 ). В первой группе вынесем за скобку общий множитель x 2, а во второй − 4 y . Получаем:
( x 3 – 3 x 2 y ) – (4 xy – 12 y 2 ) = x 2 ( x – 3 y ) – 4 y ( x – 3 y ). Теперь общий множитель ( x – 3 y ) также можно вынести за скобки:
x 2 ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x 2 – 4 y ). Ответ. ( x – 3 y )( x 2 – 4 y ).
Пример. Разложить на множители многочлен x 4 + 4 x 2
Решение. Имеем x4+4x2−1=x4+2 2x2+4−4−1=(x2+2)2−5=(x2+2−5) (x2+2−5) .
2x2+4−4−1=(x2+2)2−5=(x2+2−5) (x2+2−5) .
Иногда при разложении многочлена на множители бывают полезны следующие утверждения:
Если многочлен , где 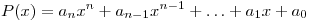 , где ≠0, с целыми коэффициентами имеет рациональный корень x0= где ), то р-делитель свободного члена, q-делитель старшего коэффициента
, где ≠0, с целыми коэффициентами имеет рациональный корень x0= где ), то р-делитель свободного члена, q-делитель старшего коэффициента
Если каким-нибудь образом подобран корень многочлена х=α многочлена Рn(х) степени n , то этот многочлен можно представить в виде
Рn(х)= (х-α)Рn-1(x), где Рn-1(x)- многочлен степени n-1.
Деление многочлена с остатком:
Важно: Для любых f(x), g(x) существуют q(x) (частное) и r(x) (остаток), такие, что f(x)=g(x)q(x)+r(x), причем степень r(x) g(x)или r(x) = 0. Многочлены g(x) и r(x) определены однозначно. Запомните следующую схему:

А) Деление «уголком»
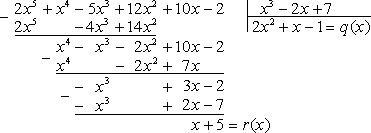
Б) Метод неопределенных коэффициентов.
Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения.
Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.
Пример. Разложить на множители многочлен 3 x 3 – x 2 – 3 x + 1.
Решение. Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены
x – p и ax 2 + bx + c такие, что справедливо равенство
3 x 3 – x 2 – 3 x + 1 = ( x – p )( ax 2 + bx + c ) = ax 3 + ( b – ap ) x 2 +
+ ( c – bp )x –pc . Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырех уравнений для определения четырех неизвестных коэффициентов:
Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1.
Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители:
3 x 3 – x 2 – 3 x + 1 = (x – 1)(3 x 2 + 2 x – 1).
Задания группе 1.
Объясните суть метода неопределенных коэффициентов.
Разложите многочлен на множители методом неопределенных коэффициентов: -5+7х-3.
.Выполните деление многочлена 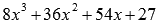 на двучлен
на двучлен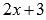 «уголком».
«уголком».
Задания группе 2.
Разложите на множители: 8а3 + 36а2 в + 54ав2 + 27в3.
Каковы могут быть степени остатка и неполного частного при делении многочлена степени 7 на многочлен степени 3?
Разделите на х-1.
Задания группе 3.
Найти все значения а, при которых уравнение 2 х 3 - 4х2 – 8х + а = 0
имеет два различных корня.
Выполнить деление многочлена на многочлен
-x+1. Найдите остаток и неполное частное.
Применив метод неопределенных коэффициентов, решите уравнение: х4 - 15х2 + 12х + 5= 0.
Тема 3: Теорема Безу и ее следствия
Дидактический материал
Этьен Безу - французский математик, член Парижской Академии Наук (с 1758 года).
Родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года.
С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.
Основные работы Этьена Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений. В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную К. Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках.
Во Франции и за её границей вплоть до 1848 года был очень популярен его шести томный “Курс математики “, который Безу писал пять лет с 1764 по 1769 год. Также, он развил метод неопределённых множителей: в элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе. Часть трудов Безу посвящена внешней баллистике.
Именем учёного названа одна из основных теорем алгебры, о которой будет говориться ниже.
Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов.
Теорема Безу утверждает, что остаток от деления многочлена 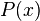 на многочлен
на многочлен 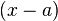 равно значению данного многочлена в точке х=а, т.е
равно значению данного многочлена в точке х=а, т.е 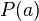 .
.
Доказательство:
Делим с остатком многочлен P(x) на многочлен (x-a):

Исходя из того, что deg R(x) - многочлен степени не выше нуля. Подставляем
 , так как
, так как  , получаем
, получаем  .
.
Но наиболее важна не именно теорема, а следствия теоремы Безу:
1. Число  - корень многочлена P(x) тогда и только тогда, когда P(x) делится без остатка на двучлен x-a.
- корень многочлена P(x) тогда и только тогда, когда P(x) делится без остатка на двучлен x-a.
Исходя из этого – множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения x-a.
2. Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (когда старший коэффициент равен единице – все рациональные корни целые).
3. Предположим, что  - целый корень приведенного многочлена P(x) с целыми коэффициентами.
- целый корень приведенного многочлена P(x) с целыми коэффициентами.
Значит, для любого целого  число
число  делится на
делится на  .
.
4.Если многочлен f(x) имеет попарно различные корни a1, a2 ,… ,an ,то он делится на произведение (x-a1)…(x-an) без остатка.
5.Многочлен степени n имеет не более n различных корней.
6.Для любого многочлена f(x) и числа a разность (f(x)-f(a)) делится без остатка на двучлен (x-a).
Теорема Безу дает возможность, найдя один корень многочлена, искать дальше корни многочлена, степень которого уже на 1 меньше: если  , то данный многочлен P(x) будет выглядеть так:
, то данный многочлен P(x) будет выглядеть так:

Таким образом, один корень найден и дальше находят уже корни многочлена  , степень которого на 1 меньше степени начального многочлена. Иногда таким методом - называется понижением степени - находят все корни данного многочлена.
, степень которого на 1 меньше степени начального многочлена. Иногда таким методом - называется понижением степени - находят все корни данного многочлена.
Следует отметить, что при решении уравнений с помощью теоремы Безу необходимо:
· найти все целые делители свободного члена;
· из этих делителей найти хотя бы один корень уравнения (a);
· левую часть уравнения разделить на (x-a);
· записать в левой части уравнения произведение делителя и частного;
· решить полученное уравнение.
Примеры:
Найти остаток от деления многочлена  на двучлен
на двучлен  .
.
Решение:
Исходя из теоремы Безу, искомый остаток соответствует значению многочлена в точке  . Тогда найдем
. Тогда найдем  , для этого значение
, для этого значение  подставляем в выражение для многочлена
подставляем в выражение для многочлена  вместо
вместо  .
.
Получаем: 
Ответ: Остаток = 5.
Задания группе 1.
Проверьте, выполняются ли условия:  делится на
делится на  .
.
Известно, что остаток от деления полинома  на
на  равен 2, от деления
равен 2, от деления  на
на  равен 1. Найдите остаток от деления
равен 1. Найдите остаток от деления  на
на  .
.
Всегда ли можно выполнить деление многочлена на многочлен?
Задания группе 2
При каких значениях a и b многочлен x4+ax3–9x2+11x+b делится без остатка на трёхчлен x2–2x+1?
Сформулируйте утверждения, которые облегчают поиск корней многочлена или уравнения.
Решите уравнение: х3-3х2-4х+12=0.
Задание группе 3
1. Докажите, что многочлен степени n имеет не более n различных корней.
2. Разложить на множители многочлен f(x)=x4+4x2–5.
3. Уравнение х3+17х2+bх-17=0 имеет три различных целых корня.
Найти b.
Тема 4: Схема Горнера.
Дидактический материал
Уильям Джордж Горнер (англ. William George Horner, 1786 — 22 сентября 1837) —британский математик, в честь которого названа схема Горнера.
Родился в 1786 году в городе Бристоль в Англии. Получил образование в Кингсвудской школе Бристоля. В возрасте 16 лет он стал помощником директора в Кингсвудской школе и директором 4 года спустя. В 1809 году уехал из Бристоля и основал свою собственную школу (The Classical Seminary) в Бате.
В 1819 году опубликовал способ приближённого вычисления действительных корней многочлена, который называется теперь способом Руффини — Горнера (этот способ был известен китайцам еще в XIII веке). Работа была напечатана в философских работах Королевского научного общества.
В XIX — начале XX века метод Горнера занимал значительное место в английских и американских учебниках по алгебре. Де Морган показал широкие возможности метода Горнера в своих работах. Умер 22 сентября 1837 года. После смерти Горнера его сын, которого тоже звали Уильям, продолжил управление школой в Бате.
Схема Горнера – способ деления многочлена
Pn(x)=∑i=0naixn−i=a0xn+a1xn−1+a2xn−2+…+an−1x+an
на бином x−a. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число a, взятое из бинома x−a:

После деления многочлена n-ой степени на бином x−a, получим многочлен, степень которого на единицу меньше исходного, т.е. равна n−1. Непосредственное применение схемы Горнера проще всего показать на примерах.
Пример: Разделить + на , используя схему Горнера.
Решение: Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена +,расположенные по убыванию степеней переменной x. Заметьте, что данный многочлен не содержит x в первой степени, т.е. коэффициент перед x в первой степени равен 0. Так как мы делим на , то во второй строке запишем единицу:

Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 5, просто перенеся его из соответствующей ячейки первой строки:

Следующую ячейку заполним по такому принципу: 1⋅5+5=10:

Аналогично заполним и четвертую ячейку второй строки: 1⋅10+1=11:

Для пятой ячейки получим: 1⋅11+0=11:

И, наконец, для последней, шестой ячейки, имеем: 1⋅11+(−11)=0:

Задача решена, осталось только записать ответ:

Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена +, полученного после деления на x−1. Естественно, что, так как степень исходного многочлена +равнялась четырём, то степень полученного многочлена на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена+ на x−1. В нашем случае остаток равен нулю, т.е. многочлены делятся нацело, то есть единица является корнем данного многочлена.
Следует учесть что, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох.
Задания группе 1
1.Объясните, в чем суть схемы Горнера.
2.Сформулируйте правило отыскания коэффициентов неполного частного
и остатка по схеме Горнера
3.Разделить многочлен x4 - 3x3 - 3x2 + 7x + 6 на двучлен x-3, используя
схему Горнера.
Задания группе 2
1.Убедиться, что числа 2 и −5 являются корнями многочлена
-.
Разделить заданный многочлен на биномы x−2 и x+5.
2.Вычислить значение многочлена 2x6 + 6x5 + x4 - 4x3 + 3x2 - x - 1
при x=-3.
3.Покажите, что многочлен  делится на двучлен
делится на двучлен
без остатка и найдите частное.
Задания группе 3
Найти корни уравнения  и разложите многочлен в левой части на множители.
и разложите многочлен в левой части на множители.
Найдите неполное частное, остаток от деления многочлена А(х) = х3 – 2х2 + 2х – 1 на двучлен х – 1.
Найдите наибольшее целое значение параметра а, при котором уравнение f(х) = 0 имеет три различных корня, один из которых х0 .
f(х) = х3 + 8х2 + ах + b, х0 = – 3.
В заключении хочется отметить, что применение этой методики повышает мотивацию обучения, интерес к предмету и развивает коммуникативные навыки учащихся.
Используемая литература:
Интернет-ресурсы:
http://fmclass.ru/math.php?id=497d9e7ae5633
http://kco-kras.ru/index.php/video/kuz_v_rvg/8_9/
http://scienceland.info/algebra8/polynomial-symmetry
http://www.microarticles.ru/article/storija-pojavlenija-mnogochlena.html
http://uztest.ru/abstracts/?idabstract=165559 http://www.pm298.ru/mnog.php http://www.cleverstudents.ru/expressions/polynomial_division_with_remainder.html http://stu.alnam.ru/book_alg-31 gimnazia-3.ru/metodika/.4.doc http://www.calc.ru/Teorema-Bezu-Skhema-Gornera.html http://www.kazreferat.info/read/izuchenie-teoremy-bezu-dlya-resheniya-uravneniy-n-y-stepeni-pri-n-2-MTAxNDQ4 http://hijos.ru/izuchenie-matematiki/algebra-11-klass/2-delenie-s-ostatkom-teorema-bezu/ http://math1.ru/education/raznoe/gorner.html http://www.menobr.ru/materials/370/5534/ izmat.by/math/polynomials/operations_polynomials
1.Алгебра и начала математического анализа, 11 класс. Часть 2 из 2. Задачник (А. Г. Мордкович и др.) 2009
2. Мкртчян М.А. и др. Теория и технология коллективных учебных занятий. Начальный курс: дистанционное учебное пособие / М.А. Мкртчян, О.В. Запятая, Г.В. Клепец и др.; Под ред. В.Б. Лебединцева
20








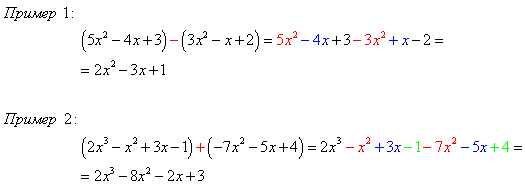
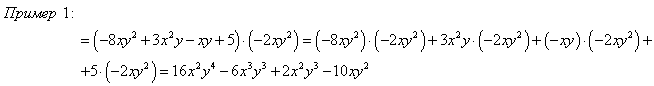
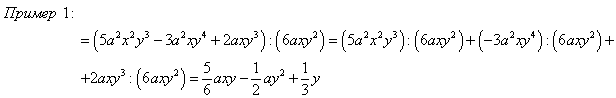
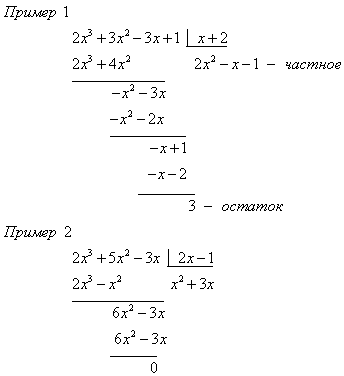
 2x2+4−4−1=(x2+2)2−5=(x2+2−5) (x2+2−5) .
2x2+4−4−1=(x2+2)2−5=(x2+2−5) (x2+2−5) .