Использование элементов стереометрии в архитектурных постройках поселка Хвойная

Муниципальное Автономное Общеобразовательное Учреждение
Средняя Школа №2 им.Е.А.Горюнова

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

На тему

«Использование элементов стереометрии в архитектурных постройках поселка Хвойная»

(Информационно-математическое направление)

Авторы исследовательской

работы:

Светлова Дарья Алексеевна,

Семёнова Мила Артёмовна, ученицы 11 класса.

Руководитель исследовательской работы:

Астанина Татьяна Сергеевна,

учитель математики.

п.Хвойная

2024-2025 уч. год

Оглавление.

Введение …………………………………………………...........................3

I. Теоретическая часть.

1.1 Что изучает стереометрия?…………………………....….…..………4

 1.2История возникновения стереометрии……………….........................5

 1.3 Где применяются стереометрические знания? ……………………..7

 1.4Объемные фигуры и происхождение их названий ………………….9

II. Практическая часть.

2.1Какие объёмные фигуры можно «увидеть» на улицах нашего посёлка?

…………………………………12

Заключение……………………………………………………..…………14

Список литературы и источников ………………………………………15

Введение.

На уроках геометрии мы познакомились со стереометрическими фигурами. При знакомстве с такими фигурами, как куб и шар, Татьяна Сергеевна показала и назвала нам еще несколько объёмных фигур. Эти фигуры со сложными названиями нас заинтересовали. Мы решили узнать о них побольше и найти их на примере архитектурных объектах нашего посёлка Хвойная.

Актуальность данного исследования обусловлена тем, что понимание взаимосвязи между архитектурой и стереометрией помогает не только лучше воспринимать окружающий мир, но и развивает пространственное мышление, что особенно важно в современном обществе.

Цель: исследовать, какие стереометрические фигуры и тела встречаются в нашем посёлке.

Задачи:

1. Рассмотреть наш посёлок с геометрической точки зрения;

2. Показать на примерах разнообразие архитектурных объектов нашего посёлка;

3. Создать презентацию «Стереометрия нашего родного посёлка».

Гипотеза исследования: архитектурные сооружения посёлка построены с использованием различных стереометрических форм и подчиняются основным законам стереометрии.

I. Теоретическая часть.

1.1 Что изучает стереометрия?

Слово "стереометрия" происходит от греческих слов "стереос" объемный, пространственный и "метрио" измерять.

Стереометрия — это раздел геометрии, изучающий свойства и отношения фигур в трехмерном пространстве.

В 10 классе на уроках геометрии мы изучили раздел данной науки – стереометрию. Она изучает особенности фигур в пространственном значении, случаи их не принадлежности поверхностей плоскостей. В данной дисциплине познаются возможности размещения плоскостей и прямых фигур по отношению к пространству, сложные фигуры: конус, призму, параллелепипед, многогранник и другие. На уроках стереометрии производится измерение площади и объема фигур.

1.2 История возникновения стереометрии.

История возникновения и развития стереометрии уходит корнями в глубокую древность.

Первые зачатки стереометрии появились в Древнем Египте, где строители и архитекторы использовали принципы трехмерной геометрии при создании своих грандиозных сооружений. Наиболее ярким примером служат пирамиды, при строительстве которых египтяне применяли различные методы измерения углов и длин для точного построения конструкций.

Следующий важный этап развития стереометрии связан с Древней Грецией. Именно здесь она заняла центральное место среди математических наук. Величайший древнегреческий ученый Евклид создал фундаментальный труд “Начала”, где изложил основные правила и принципы стереометрии. В этой работе были сформулированы важнейшие понятия о объеме, поверхности и угле, а также впервые представлены аксиомы и доказательства, ставшие фундаментом геометрии. Евклид доказал множество теорем, связанных с объемами и площадями пространственных фигур, включая знаменитую формулу для вычисления объема шара.

В период Средних веков и эпохи Возрождения развитие стереометрии продолжилось. Значительный вклад в ее развитие внесли такие выдающиеся ученые, как Жан Даламбер, Архимед и Рене Декарт. Особенно важным стало изобретение Декартом системы координат, которая позволила точно определять местоположение пространственных объектов и решать сложные геометрические задачи.

В эпоху Возрождения стереометрия получила новый импульс развития благодаря работам таких выдающихся деятелей, как Леонардо да Винчи, ДжероламоКардано и Альбрехт Дюрер. Они не только развивали теоретические аспекты науки, но и применяли ее на практике в искусстве и архитектуре. Например, в знаменитой картине “Тайная вечеря” Леонардо да Винчи использовал правила перспективы и объема для создания иллюзии глубины и трехмерности.

В XIX веке развитие стереометрии продолжилось благодаря работам математика Жоржа Лиувилля, который разработал метод интегрирования для вычисления объемов сложных тел. Это позволило существенно расширить представления о трехмерных фигурах и создать более совершенную математическую основу для стереометрии.

Таким образом, стереометрия прошла долгий путь развития от практических потребностей древних строителей до современной математической науки, которая находит применение в различных областях: от архитектуры и инженерии до компьютерной графики и медицины.

1.3 Где применяются стереометрические знания?

Стереометрические знания находят широкое применение в различных областях человеческой деятельности:

1. Архитектура и строительство:

• Проектирование зданий и сооружений

• Создание трехмерных моделей конструкций

• Расчет прочности и устойчивости конструкций

• Планирование пространственной организации помещений.

1. Инженерное дело и производство:

• Проектирование механизмов и машин

• Разработка технологических установок

• Расчет оптимальных форм деталей

1. Компьютерная графика и дизайн:

• Создание 3D-моделей

• Разработка компьютерной анимации

• Проектирование виртуальной реальности

• Создание спец эффектов в кино

1. Медицина:

• Медицинская визуализация

• Создание трехмерных моделей органов

• Планирование хирургических операций

1. Астрономия:

• Изучение формы космических тел

• Расчет объемов небесных объектов

• Моделирование движения планет

1. Образование:

• Развитие пространственного мышления

• Формирование навыков моделирования

• Обучение техническому черчению

Практическое применение стереометрии постоянно расширяется с развитием технологий. Современные 3D-принтеры, системы виртуальной реальности и компьютерного моделирования во многом основаны на принципах стереометрии. Эти знания становятся все более востребованными в связи с растущей необходимостью создавать сложные трехмерные модели в различных областях деятельности человека.

Особенно важно отметить, что стереометрические знания помогают развивать пространственное мышление, которое является ключевым навыком для многих современных профессий. Умение визуализировать и анализировать трехмерные объекты становится все более ценным в эпоху цифровизации и развития технологий виртуальной реальности.

1.4 Объемные фигуры.

Многогранники.

Многогранник - это такое тело, поверхность которого состоит из конечной числа плоских многоугольников. Многогранник называется выпуклым, если он лежит по одну сторону от плоскости каждой из плоских многоугольников на его поверхности. Общая часть такой плоскости и поверхности выпуклого многоугольника называется гранью.
На рисунке ниже слева изображен не выпуклый многогранник; на рисунке справа - выпуклый.

Г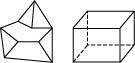 рани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины граней - вершинами многогранника.

Пирамида - это многогранник, одна грань которого многоугольник, а остальные грани - треугольники с общей вершиной. Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина её отсекается плоскостью.

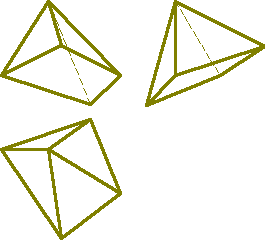
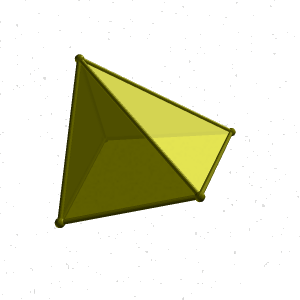
Призма - многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани параллелограммы.

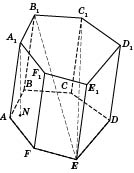
Прямая призма — это призма, у которой боковые ребра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками. Другие призмы называются наклонными.

Прямая прямоугольная призма называется также прямоугольным параллелепипедом.

Правильная призма — это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники.

Параллелепипед — это четырехугольная призма, все грани которой — параллелограммы.

Параллелепипеды, как и призмы, могут быть наклонными и прямыми.

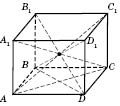
Прямой параллелепипед, основанием которого служит прямоугольник, называют прямоугольным параллелепипедом.

У прямоугольного параллелепипеда все грани — прямоугольники.

Длины трех ребер прямоугольного параллелепипеда, имеющих общее начало, называют его измерениями.

Тела вращения.

Тела вращения — объемные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.

Виды тел вращения, свойства и чертежи

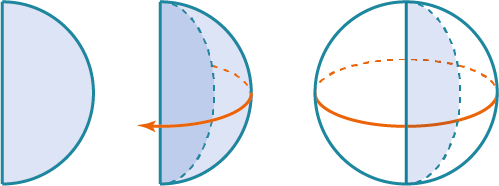Шар — образован полукругом, вращающимся вокруг диаметра разреза

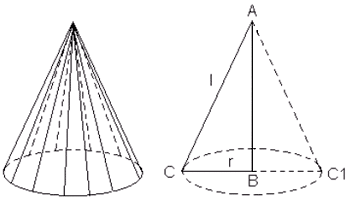
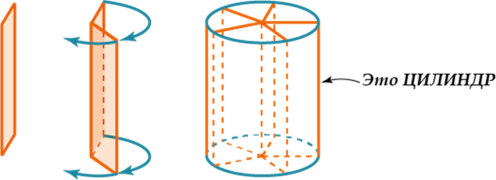
Цилиндр − это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Цилиндрическая поверхность образуется движением прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой, которая называется направляющей. Указанная прямая является образующей цилиндрической поверхности.

Цилиндр  образован прямоугольником, вращающимся вокруг одной из сторон

За площадь боковой поверхности цилиндра принимается площадь его развёртки

Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов

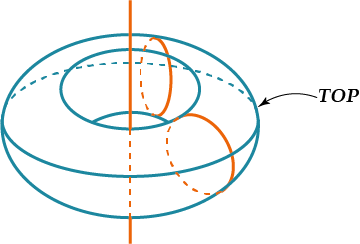
Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его

II. Практическая часть.

2.1 Какие объемные фигуры можно «увидеть» на улицах нашего поселка?

Мы прогулялись по нашему поселку и сфотографировали сооружения, которые состоят из различных объемных фигур.

Примеры архитектурных объектов

Конечно, большинство архитектурных сооружений поселка являются сложными объектами, отдельные части которых имеют форму различных геометрических тел, т.е можно говорить о комбинациях различных тел. Рассмотрим некоторые здания нашего поселка Хвойная.

1.На Крсаноармейской улице

находится Пестовский район-

ный суд, здание которого

представляет собой прямо-

угольный параллелепипед.

Здание имеет шесть граней,

каждая из которых прямоуголь-

ник. Все углы прямые - это

признаки прямоугольного

параллелепипеда.

2.Памятник, расположенный

между улицами Красных Зорь

и Красноармейская, состоит из двух

объемных фигур: верхняя часть представ-

ляет собой усеченную четырехгранную

пирамиду и нижняя -усеченную парамиду,

служащую основанием конструкции. Эти

стереометрические формы подчеркивают

строгую геометрию памятника и придают

ему торжественный вид.

3.В основе здания продуктового магазина "Свежий хлеб" лежат две стереометрические фигуры: призма образующая

о сновную часть строения, и

четырехгранная пирамида с

прямоугольным основанием,

формирующая крышу.

4.Здание почты также состоит из прямоугольных параллелепипедов, которые формируют основной объем и отдельные архитектурные элементы фасада. Также в конструкции здания можно выделить элементы, выполненные в виде прямоугольных призм - например, выступы на фасаде. Эта постройка является наглядным примером применения стереометрических фигур в архитектуре нашего поселка Хвойная.

На улицах нашей Хвойной также можно встретить архитектурные

сооружения, имеющие форму тел вращения. Это и

колонны зданий, и купола церквей.

5 .Фасад второго корпуса школы №2 имени Е.А.Горюнова украшен рядом колонн, имеющих форму цилиндра, что четко видно по ее круглому основанию и равномерной высоте. Эти элементы не только выполняют архитектурную функцию, но и наглядно демонстрируют стереометрическую фигуру - цилиндр.

7 .Н а фотографиях изображена церковь Никандра Городноозерского. В основе здания можно выделить стереометрическую фигуру - прямоугольный параллелепипед, образующий основной объем церкви. Купола церкви состоят из различных стереометрических фигур. Верхняя часть главного купола - это шар, под которым расположен цилиндр. Основной высокий шпиль имеет форму конуса, что хорошо видно на колокольне.

Заключение

В своей работе мы исследовали, какие геометрические фигуры и тела окружают нас, и убедилась, сколько самых разнообразных геометрических линий и поверхностей использует человек в своей деятельности - при строительстве различных зданий, мостов, машин, в транспорте.

Все архитектурные сооружения поселка Хвойная состоят из геометрических фигур и их совокупностей. Чаще встречается – параллелепипед, такую форму имеют все жилые дома и различные учреждения. Это объясняется в первую очередь тем, что такая форма более удобна для проживания, проще при строительстве. Но развитие строительной индустрии позволяет создавать здания более сложных, интересных форм, придающих индивидуальность каждому объекту. Геометрия украшает город, придает ему строгость, индивидуальность и красоту.

Следует отметить до начала работы над темой, я не замечала или мало задумывалась о геометрии окружающего нас мира, теперь же из всего сказанного делаю вывод, что геометрия в нашей жизни на каждом шагу и играет очень большую роль.

Список источников

Геометрия 10-11 классы: учеб. для общеобразоват.учреждений: базовый и профил.уровни / [Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др.]- М.: Просвещение, 2011

http://uztest.ru/abstracts/?id=57&t=6

http://vikidalka.ru/1-46130.html

https://ru.wikipedia.org/wiki/%D0%A6%D0%B8%D0%BB%D0%B8%D0%BD%D0%B4%D1%80

http://www.cleverstudents.ru/line_and_plane/straight_line_in_the_space.html

http://worldtravelserver.ru/travel/ru/russia/ivanovo/gallery_ivanovo.html

21