Использование графика и свойств функции y = 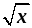
при решении различных задач
Цели: продолжить формирование умения строить график функции y =  и использовать её свойства при решении различных задач.
и использовать её свойства при решении различных задач.
Ход урока
I. Организационный момент.
II. Устная работа.
– Определите, принадлежат ли графику функции y =  следующие точки:
следующие точки:
а) А (49; 7); в) С 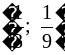 ;
;
б) В (–36; 6); г) D 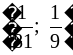 .
.
III. Формирование умений и навыков.
1. Сравните числа:
а) 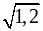 и
и 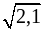 ; в)
; в) 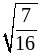 и
и 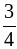 ;
;
б) 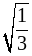 и
и 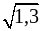 ; г) 2,7 и
; г) 2,7 и 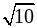 .
.
2. Расположите числа в порядке убывания:
а) 5; 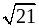 ;
; 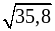 ; 7
; 7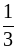 ;
;
б) 0,25; 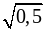 ;
; 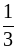 и
и 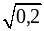 .
.
3. № 358, № 362 (а).
4. № 359.
Р е ш е н и е
Чтобы доказать, что графики функций y =  и у = х + 0,5 не имеют общих точек, достаточно их построить.
и у = х + 0,5 не имеют общих точек, достаточно их построить.
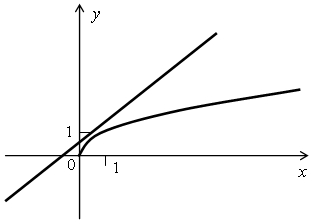
Можно эту задачу решить аналитически, показав, что с увеличением значений аргумента значения функции у = х + 0,5 увеличивается быстрее, чем значения функции y =  .
.
5. № 360 (а, в), № 361.
В классе с высоким уровнем подготовки можно дополнительно выполнить № 475.
Р е ш е н и е
а) Построим график функции y =  и будем относительно него передвигать прямые вида y = x + b. Это параллельные прямые, которые образуют острый угол с положительным направлением оси абсцисс.
и будем относительно него передвигать прямые вида y = x + b. Это параллельные прямые, которые образуют острый угол с положительным направлением оси абсцисс.
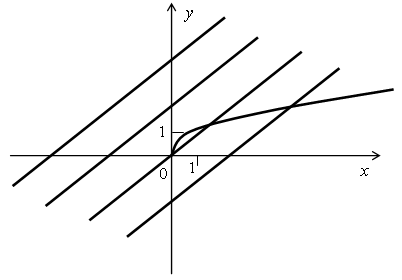
Таким образом, очевидно, что уравнение  = x + b может иметь один, два корня, а может и не иметь корней.
= x + b может иметь один, два корня, а может и не иметь корней.
б) Прямые вида y = –x + b – это параллельные прямые, которые образуют тупой угол с положительным направлением оси абсцисс.
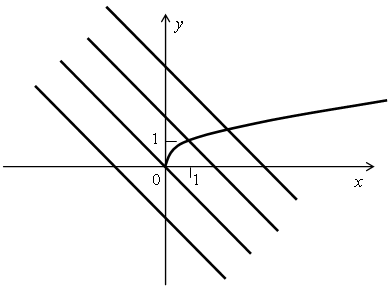
Получаем, что уравнение  = –x + b имеет либо один корень, либо не имеет корней.
= –x + b имеет либо один корень, либо не имеет корней.
IV. Проверочная работа.
В а р и а н т 1
1. Постройте график функции y =  . По графику найдите:
. По графику найдите:
а) значение функции при х = 1; 3; 4; 6;
б) значение аргумента, которому соответствует значение y =  ; 1; 1,8; 3.
; 1; 1,8; 3.
2. Принадлежит ли графику функции y =  точка:
точка:
а) А (36; 6); б) В (–9; 3); в) С ?
3. Сравните числа:
а)  и
и  ; в) 2 и
; в) 2 и  ;
;
б)  и
и  ; г)
; г)  и 2.
и 2.
В а р и а н т 2
1. Постройте график функции y =  . По графику найдите:
. По графику найдите:
а) значение функции при х = 0; 2; 5; 9;
б) значение аргумента, которому соответствует значение y = 0,49; 1,5; 2 ; 2,8.
; 2,8.
2. Принадлежит ли графику функции y =  точка:
точка:
а) А (81; 9); б) В (–16; 4); в) С ?
3. Сравните числа:
а)  и
и 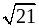 ; в) 3 и
; в) 3 и  ;
;
б)  и
и 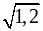 ; г)
; г)  и 4.
и 4.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какими свойствами обладает функция y =  ?
?
– Как сравнить два квадратных корня?
– Сколько общих точек могут иметь графики функций y = 
и y = kx + b?
Домашнее задание: № 360 (б, г), № 362 (б), № 365.







 и использовать её свойства при решении различных задач.
и использовать её свойства при решении различных задач. ;
; .
.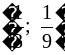 ;
;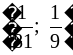 .
.






















