Использование метода координат при решении стереометрических задач

МБОУ покровская средняя общеобразовательная школа № 1 с УИОП Использование метода координат при решении стереометрических задач Иванова Саргылана Семеновна учитель математики МБОУ «ПСОШ № 1 с УИОП» Стаж работы: 15 лет Категория: высокая

Цель работы:

• Раскрыть содержание метода
• Показать применение метода при решении конкретных задач
• Решить сложные стереометрические задачи с использованием метода

Объект исследования:

решение стереометрических задач из ЕГЭ в блоке (задание С2)

Предмет исследования:

способы решения стереометрических задач методом координат

Гипотеза:

1 ) Через решение задач на нахождение расстояний и углов в пространстве двумя способами (геометрический и метод координат ) сделать вывод о преимуществе метода координат для решения ряда задач этого блока.

2) Расширить представление о применении метода координат в решении стереометрических задач на построение сечения.

3) Применяя метод координат успешно решить стереометрические задачи из ЕГЭ в блоке С (задание С2).

Содержание работы

Содержание

Введение……………………………………………………………………………… 3

Теоретические сведения

Полезные замечания о методе координат……………………………………6

Общий алгоритм решения задач методом координат ………………………6

Примеры удобного задания системы координат…………………………….9

Способы решения следующих видов стереометрических задач методом координат

2.1. Нахождение угла между прямыми………………………………………………11

2.2. Нахождение угла между прямой и плоскостью………………………………...12

2.3. Нахождение угла между двумя плоскостями……………………………………14

Решение аналогичных заданий ЕГЭ методом координат……………………… 30

Заключение……………………………………………………………………………. 34

Список использованной литературы ……………………………………………… 36

Любую задачу С2 можно решить методом координат.

Метод координат – не единственный метод решения задач С2

Метод координат универсален, потому что есть алгоритм решения для любого типа заданий С2.

систему координат специальным способом для разных объектов.

изображать плоскость Оху и основание геометрического тела в ней отдельно.

Общий алгоритм для решения С2 методом координат

1. Ввести прямоугольную систему координат (выбор зависит от объекта).

2. Выписать координаты всех необходимых точек.

3. Вычислить координаты необходимых векторов.

4. Применить формулу, выполнить вычисления.

5. Записать ответ.

Способы решения стереометрических задач

Поэтапно вычислительный

Метод координат

Этот способ требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической

Другой метод - применение векторов и координат. Это простые формулы, алгоритмы и правила.

То есть рассматриваем задачу в трехмерной системе координат

Общий алгоритм для решения С2 методом координат

1. Ввести прямоугольную систему координат (выбор зависит от объекта).

2. Выписать координаты всех необходимых точек.

3. Вычислить координаты необходимых векторов .

4. Применить формулу, выполнить вычисления.

5. Записать ответ.

Углы в пространстве

Угол между

Прямыми

а и в

Угол между

прямой а

и плоскостью α

Угол между

плоскостями

α и β

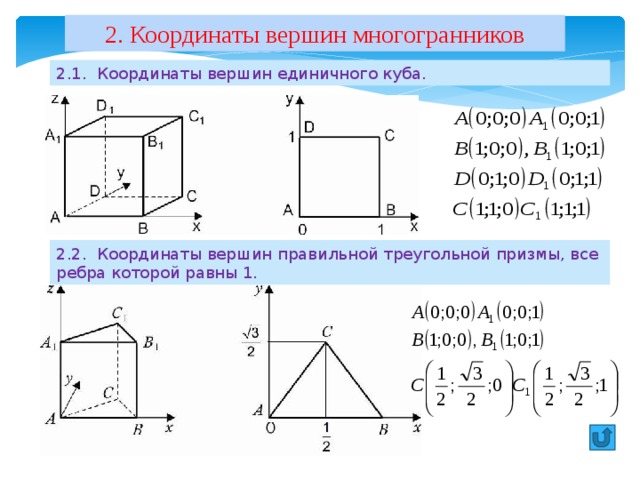
2. Координаты вершин многогранников

2.1. Координаты вершин единичного куба.

2.2. Координаты вершин правильной треугольной призмы, все ребра которой равны 1.

2.3. Координаты вершин правильной шестиугольной призмы,

все ребра которой равны 1.

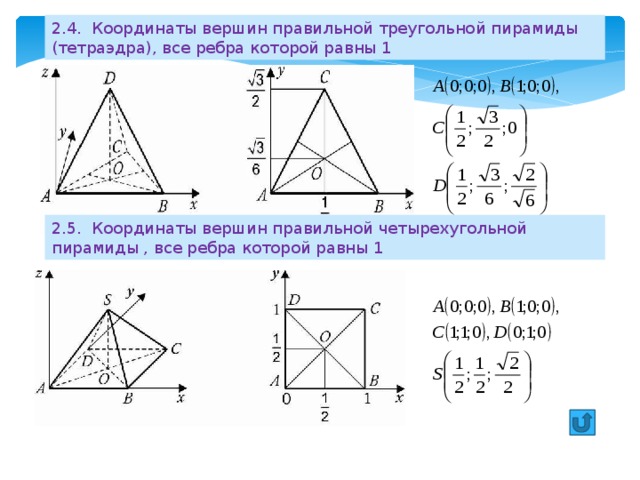
2.4. Координаты вершин правильной треугольной пирамиды (тетраэдра), все ребра которой равны 1

2.5. Координаты вершин правильной четырехугольной пирамиды , все ребра которой равны 1

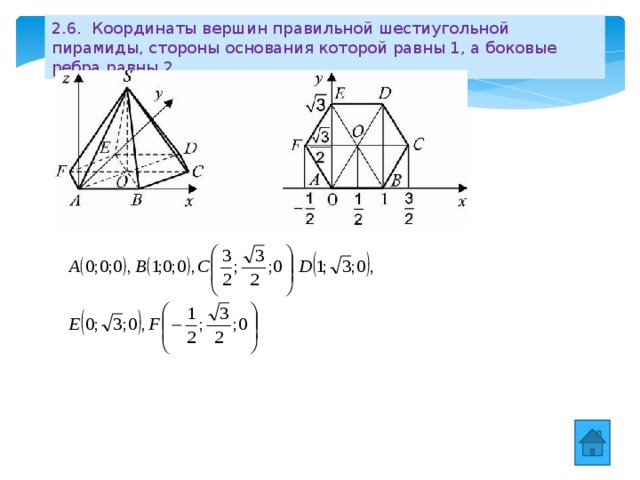
2.6. Координаты вершин правильной шестиугольной пирамиды, стороны основания которой равны 1, а боковые ребра равны 2

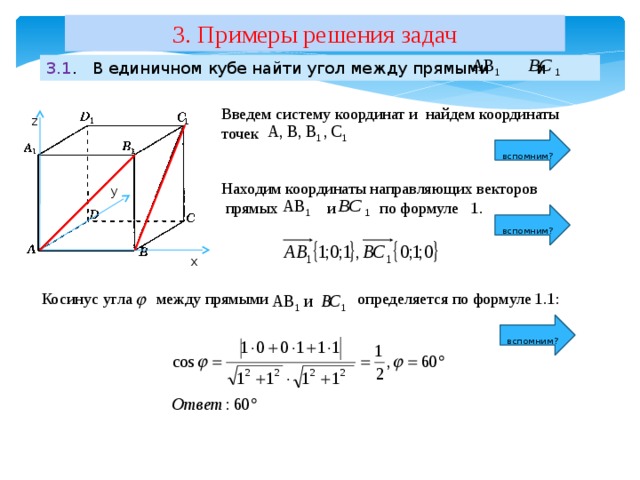
3. Примеры решения задач

3.1 . В единичном кубе найти угол между прямыми и

Введем систему координат и найдем координаты

точек

z

вспомним?

Находим координаты направляющих векторов

прямых и по формуле 1.

y

вспомним?

х

Косинус угла между прямыми определяется по формуле 1.1:

вспомним?

3.2. В правильной шестиугольной призме , все ребра которой равны 1, найти угол между прямой AF и плоскостью

Введем систему координат и находим координаты нужных точек.

вспомним?

z

Найдем координаты вектора

Плоскость совпадает с плоскостью грани

; зададим ее с помощью точек

y

Пусть ax+by+cz+d=0 – уравнение плоскости

х

Уравнение плоскости примет вид

Вектор нормали :

Синус искомого угла:

вспомним?

7

ЗАКЛЮЧЕНИЕ

В процессе работы над темой «Использование метода координат при решении стереометрических задач» я:

• Изучили литературу по данному вопросу. Познакомился с двумя способами решения стереометрических задач. Рассмотрел различные задачи ЕГЭ из блока С
• Изучили литературу по данному вопросу.
• Познакомился с двумя способами решения стереометрических задач.
• Рассмотрел различные задачи ЕГЭ из блока С

и пришел к выводу:

• В ряде случаев при решении стереометрических задач возможно, решать задачи по правилам, а иногда удобнее воспользоваться методом координат
• При решении задач из блока С2, метод координат имеет преимущества перед другими тем, что не требует сложных построений в проекциях. По той простой причине, что этот метод заключается во введении декартовой системы координат, а затем – исчислении образующихся векторов. Единственный его, пожалуй, недостаток – это требуемый нередко большой объем вычислений.
• С помощью метода координат можно быстро и успешно решать стереометрические задачи из ЕГЭ в блоке С (задание С2).