Использование метода рационализации в задании № 15 ЕГЭ по математике профильного уровня

Использование метода рационализации при решении неравенств

в задании № 15

профильного уровня ЕГЭ по математике

Подготовила:

учитель математики

ГБОУ «Школа № 67 г.о. Донецк»

Бажанова Наталья Борисовна

История метода рационализации

Метод рационализации известен более 50 лет, встречался под названиями

• метод замены множителей
• Метод декомпозиции
• Обобщенный метод интервалов
• метод знакотождественных множителей

Теоретическая основа метода рационализации

• Два неравенства называются равносильными, если множество их решений совпадает
• Если f(x) — монотонно возрастающая функция, то разность f(a)-f(b) совпадает по знаку с разностью a-b. 
• Если f(x) — монотонно убывающая функция, то разность f(a)-f(b) совпадает по знаку с разностью b-a

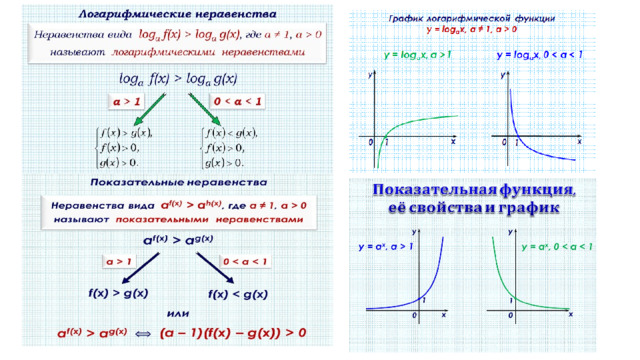
• Метод рационализации позволяет перейти от неравенства содержащего сложные логарифмические и показательные иррациональные выражения к равносильному ему рациональному неравенству.

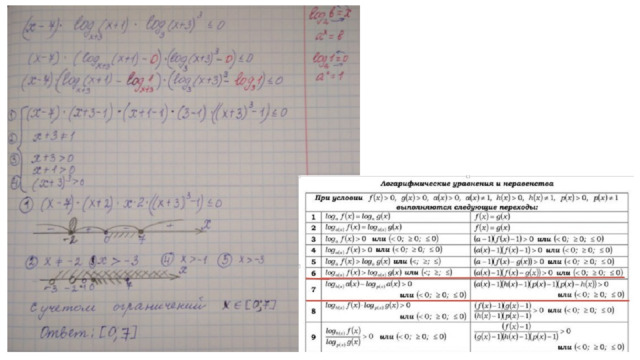
Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x), при котором неравенство G(x) 0 равносильно неравенству F(x) 0 в области определения выражения F(x).

• Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени.
• Рассмотрим таблицы, позволяющие рационализировать логарифмические неравенства(заметим, что рационализация производится на ОДЗ)

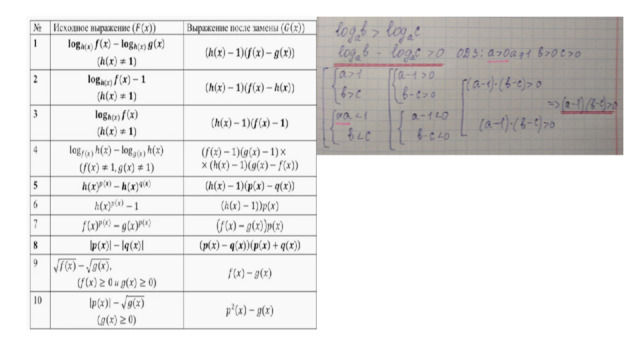
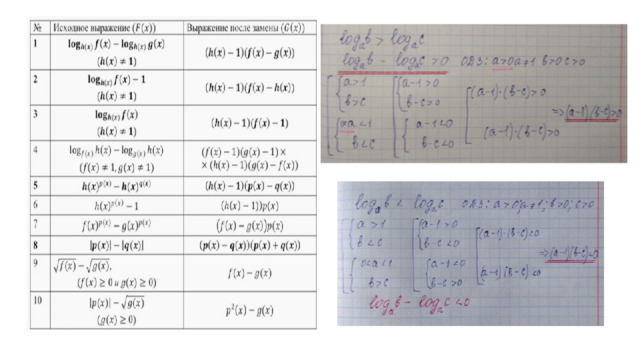
Метод рационализации применяется только при решении неравенств

3. В правой части неравенства должен стоять 0

2. Используя метод рационализации (метод замены множителей) можно заменять только множители, а не слагаемые