Использование моделирования
при формировании математической грамотности младших школьников
Using the simulation the formation of mathematical literacy younger students
В статье рассматривается моделирование как средство формирования ма- тематической грамотности младших школьников. Основными формами моде-

лирования являются таблицы, схемы, кластеры, чертежи. В статье анализирует- ся содержание учебников математики начальной школы разных авторов с пози- ций использования наглядных средств для формирования математической гра- мотности.
Материал статьи актуален, так как знакомит учителей начальных классов с некоторыми формами представления учебного материала по математике.
The article deals with modeling as a means of forming mathematical literacy younger students. The main forms of modeling are tables, charts, clusters drawings. The article analyzes the content of the textbooks of elementary school mathematics by various authors on the use of visual aids for the formation of mathematical literacy.
The material is relevant, since introduces elementary school teachers with some forms of representation for learning math.
Ключевые слова: математическая грамотность, моделирование, таблица, схема, кластер, младшие школьники.
Key words: mathematical literacy, modeling, tables, charts, cluster, younger students.
Федеральный государственный образовательный стандарт выдвинул кон- кретные требования к выпускнику начальной школы. Считается, что овладение метапредметными результатами вместе с проявлением волевых качеств лично- сти составляет основу умения учиться и определяет младшего школьника как субъекта учебной деятельности. Выходя за рамки учебной деятельности, млад- ший школьник действует как субъект собственной жизнедеятельности и явля- ется конструктором собственного жизненного пути, проявляя себя как личность созидающая, творческая, готовая решать жизненные проблемы. Поэтому сего- дня актуальной становится проблема организации обучения, направленного на сознательное формирование способов действий, необходимых для решения проблем, и достижение на их основе метапредметных результатов обучения.
Именно в начальной школе развиваются познавательные способности, формируются и обобщаются понятия, мировоззренческие убеждения. Поэтому знакомство с основами математической грамотности, а, следовательно, и фор- мирование информационной грамотности, должно начинаться в период обуче- ния ребенка в 1-4 классах, поскольку запоздалое формирование одних струк- турных компонентов информационной грамотности (культуры) в силу психоло-
гических особенностей развития личности может привести к невозможности развития других [1, С. 152].
Освоение содержания математического образования младшими школьни- ками должно быть ориентировано на понимание математической информации. Понимание означает интеграцию, дифференциацию, сравнение данных об объ- ектах. Ориентация на понимание является одним из условий развития матема- тической грамотности учащихся.
Математическая грамотность, по словам А.А. Леонтьева, предусматрива- ет способность человека использовать приобретенные в течение жизни знания для решения широкого диапазона жизненных задач в различных сферах чело- веческой деятельности, общения и социальных отношений [39, С. 6].
С. Березин дает такое понимание математической грамотности: «Матема- тическая грамотность – умение правильно применять математические термины, наличие необходимых математических знаний и сведений для выполнения ра- боты (решение проблемы) в конкретной предметной области» [26, С. 4].
Не секрет, что математическая информация трудна для восприятия некоторой группой учащихся. Для того чтобы математические знания были посильны большей части обучаемых, необходимо подбирать особые средства обучения. К некоторым из них можно отнести наглядные средства обучения: таблицы, схемы, графики, рисунки и т.д. Поэтому для формирования математической грамотности очень важно научить детей работать с таблицами, алгоритмами, памятками и т.п.
Визуализации в педагогике уделяется важное внимание, т.к. для прочного усвоения знаний необходимо восприятие информации органами чувств. К.Д. Ушинский указывал, что наглядность отвечает психологическим особенностям детей, мыслящих «формами, звуками, красками, ощущениями». Наглядное обучение К.Я. Ушинский определял как «такое учение, которое строится не на отвлеченных представлениях и словах, а на конкретных образах, непосредст- венно воспринятых ребенком».

В начальных классах учащиеся учатся понимать информацию, представ- ленную различными способами – составлением графических и символических моделей для установления количественных и причинно-следственных связей.
Моделирование – это метод опосредованного познания, при котором изучается не интересующий нас объект, а его заместитель (модель), находящийся в некотором объективном соответствии с познавательным объектом, способный замещать его в определённых отношениях и дающий при этом новую информацию об объекте.
В ходе беседы с учителями начальных классов установлено, что все ре- ципиенты используют в своей работе схемы, 84% учителей применяют табли- цы, 77% – чертежи, 27% – диаграммы, 10% – кластер; никто из опрошенных не применяет такой способ работы с информацией, как пазл.
Проанализировав учебники математики Л.Г. Петерсон, М.И. Моро, Т.Е. Демидовой, мы сделали вывод, что программами предусмотрено целенаправ- ленное формирование совокупности умений работать с информацией: читать и заполнять таблицы, читать готовые столбчатые и круговые диаграммы, дост- раивать столбчатую диаграмму, сравнивать и обобщать информацию, пред- ставленную в строках и столбцах таблиц и диаграмм, распознавать одну и ту же информацию, представленную в разной форме.
Рассмотрим некоторые примеры моделирования на уроках математики, связанные с формированием математической грамотности младших школьни- ков.
Кластер (англ. Cluster – пучок, гроздь) – объединение нескольких однородных элементов, которое может рассматриваться как самостоятельная единица, обладающая определенными свойствами.
В методике «кластер» – это карта понятий, которая позволяет ученикам свободно размышлять над какой-либо темой, дает возможность оценить свои знания и представления об изучаемом объекте, помогает развивать память.
Кластер позволяет школьникам выделить узловые моменты темы, разделить информационный текст на основной и дополнительный, сосредоточиться на главном. Такой вид работы помогает систематизировать знания обучающихся, обеспечивает усвоение информации на уровне понимания, что является необходимым при формировании математической грамотности. Является одним из способов рефлексии.
На рисунке 1 изображен кластер, систематизирующий знания по теме
«Прямоугольник». Используя наглядно представленную информацию, все учащиеся смогут описать понятия, связанные с прямоугольником.

Рис. 1
Следующий способ работы с информацией – таблицы – это текстовые или числовые записи, располагаемые в определённом порядке.
Виды таблиц: концептуальная таблица, сводная таблица, таблица-синтез. Концептуальная таблица – используется при сравнении нескольких объ-
ектов по нескольким вопросам.
В зависимости от цели, поставленной на уроке, таблица может заполнять- ся учащимися на уроке или дома, постепенно или вся целиком как результат обобщения. Затем проводится обсуждение правильности заполненного мате- риала, уточнение, дополнение, исправление; сравнение сил.
Анализ информации практического содержания представлен в таблицах 1 и 2.

Цены на билеты в кинотеатр, рубли
Таблица 1
| Билеты | Дни недели |
| понедельник | вторник | среда | четверг | пятница | суббота | воскресенье |
| детский | 100 | выход- ной | 120 | 120 | 120 | 150 | 150 |
| взрослый | 150 | 180 | 180 | 180 | 250 | 250 |
Работа по данным таблицы.
Правильно ли, что в таблице представлены цены на детские и взрослые билеты в кинотеатр.
На какой день в кинотеатре нельзя купить билет?
Сводная таблица – позволяет за короткое время описать и изучить боль- шое количество информации, помогает ее систематизировать, проводить па- раллели между явлениями, событиями или фактами. При составлении таблиц учащиеся могут сами выбирать объекты сравнения или линии сравнения.
Составление сравнительных таблиц можно использовать как на этапе ак- туализации знаний, так и на этапе открытия новых знаний, рефлексии. На этапе актуализации знаний лучше всего попросить ребят заполнять ее карандашом, так как после работы с текстом у детей могут возникнуть исправления, которые выполняются ручкой. Общее лучше обводить красной ручкой. Сводная таблица позволяет более качественно подготовить домашнее задание, так как является уже готовой памяткой, сделанной на уроке.
Таблица-синтез – позволяет по представленным данным описать ситуа- цию. Учащимся предлагается подобрать ключевые слова, фразы, которые, как им кажется, могут быть опорными в тексте, предлагаемом для изучения впо- следствии. Представим образец задачи, условие которой необходимо вставить в столбцы таблицы.
Задача. Внимательно прочтите текст «Оценки за год» и составьте таблицу.
У Мухина по литературе оценка за год «3» У Алексеевой по математике оценка за год – «5». У Дроздова по природоведению оценка за год «5». У Галкина по природоведению оценка за год – «5». У Прозоровой по литературе
оценка за год – «5». У Радугиной по математике оценка за год «4». У Алексеевой по природоведению оценка за год «5». У Дроздова по русскому языку оценка за год «4». У Алексеевой по русскому языку оценка за год – «5». У Алексеевой по литературе оценка за год – «5». У Дроздова по математике оценка за год – «5». У Мухина по математике оценка за год – «3». У Мухина по русскому языку оценка за год – «3». У Прозоровой по математике оценка за год
– «5». У Прозоровой по русскому языку оценка за год «5». У Радугиной по русскому языку оценка за год – «4».
Попытайтесь ответить на следующие вопросы:
Об оценках скольких учеников говорится в этом тексте?
По каким предметам приведены годовые оценки учеников?
Сколько учеников имеют только отличные оценки?
Кто из учеников имеет «4» и «5» по математике?
В издательском словаре схема – иллюстрация, которая с помощью условных графических обозначений передает суть строения предмета или системы, показывает характер процесса, движения, структуру и т. д.
Рассмотрим такие задания-схемы.
Дорисуй и допиши. Сделай вывод.
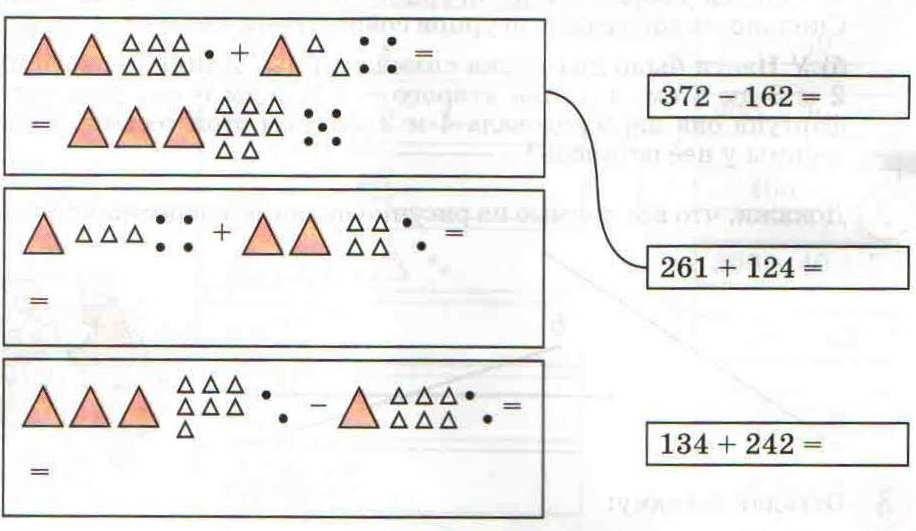

Составь и реши задачи по схемам:
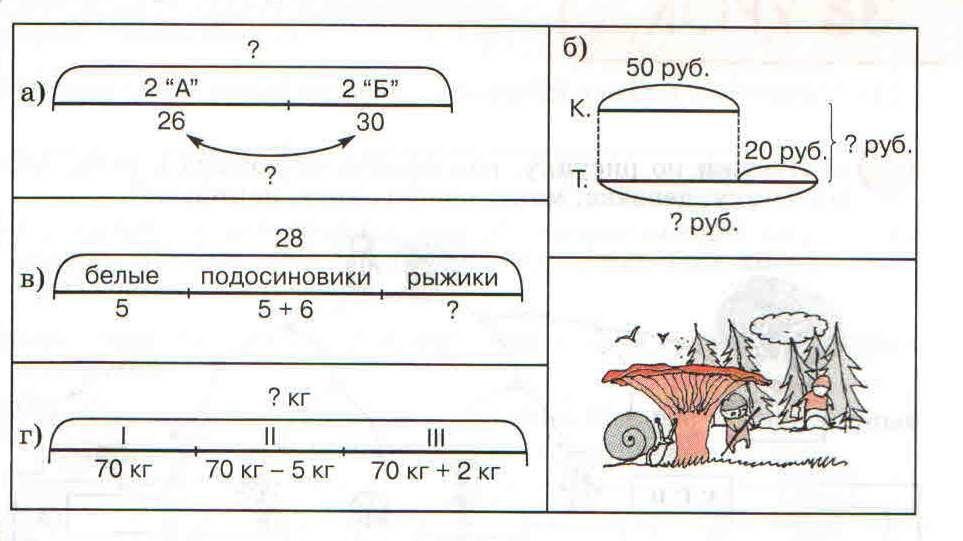
Такой вид работы позволил обучающимся применить жизненный опыт к составлению и решению задач. Это позволило реализовать практико- ориентированный характер конструирования учебной информации.
Еще одним способом работы с информацией математического содержания являются чертежи – условное изображение предметов, взаимосвязей между ними и взаимоотношения величин с помощью отрезков и с соблюдением определенного масштаба.
В начальной школе встречаются задачи, которые необходимо решить арифметическим способом. Решение таких задач не связано с введением новой переменной, как это принято в старших классах, что вызывает затруднения оформления решения. В этом случае значительно облегчает решение схема, со- ставленная по условию задачи. Рассмотрим задачу, решение которой выполне- но арифметическим способом.
Задача. Коля съел 1/3 всех яблок и еще 2 яблока, Ваня съел ¼ и еще 1 яб- локо, а Толя – половину всех яблок, которые остались после Коли и Вани. По- сле этого осталась 1/6 часть первоначального числа яблок. Сколько яблок было вначале?
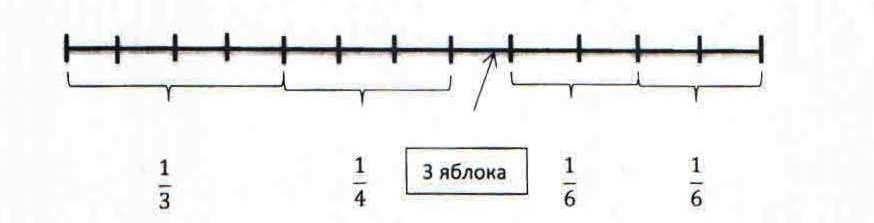
1 – (1/3 + ¼ + 1/6 + 1/6) = 1/12 всех яблок составляют 3 яблока.
312 36 (ябл.) было вначале.
Ответ: 36 яблок.
Таким образом, представленные графические способы работы с информацией: кластер, схемы, таблицы, чертежи помогут учителю сформировать у детей умение работать с информацией на уроках математики, что в свою очередь обеспечит формирование математической грамотности младших школьников.
Библиографический список
Волкова, С.И. Математика. Методические рекомендации 2 класс. Пособие для учителей [Текст] / С.И. Волкова, М.А. Бантова, Г.В. Бельтюкова. – М.: Просвещение, 2013. – 160 с.
Немов, Р.С. Психология: Учебник для студентов высш. ᴨед учеб. заведений: В 3 кн. – Кн. 2. Психология образования. – 3-е изд. [Текст] / Р.С. Немов. – М.: Гуманит. изд. центр ВЛАДОС, 1997. – 608 с.
Истомина, Н.Б. Методика обучения математике в начальных классах [Текст] / Н.Б. Истомина. – М., Издательский центр «Академия». – 2000. – 288 с.
Современные образовательные технологии: учебное пособие / Коллектив авторов; под ред. Н.В. Бордовской. – 3-е изд., стер. – М.: КНОКУС, 2013. – 432 с.
Bibliography
Volkova, SI Mathematics. Guidelines 2 class. Handbook for Teachers [Text] / SI Volkova, MA Bantova, GV Beltyukova. – M.: Education, 2013. – 160 p.
Nemov, RS Psychology: textbook for university students. ᴨed studies. Institutions: In 3 Vol. – KH. 2. Educational Psychology. – 3rd Ed. [Text] / RS Nemov. – M.: humanity. ed. VLADOS Center, 1997. – 608 p.
Istomin, NB Methods of teaching mathematics in the elementary grades [Text] / N.B. Istomina. – M., Publishing Center "Academy". – 2000. – 288 p.
Modern educational technology: a tutorial / Number Lect authors; Ed. NV Bordovskikh.
- 3rd ed., Sr. – M.: KNOKUS, 2013. – 432 p.
1






















