Использование приемов абстрактного мышления в работе с одаренными детьми на уроках математики
“Важнейшая задача цивилизации – научить человека мыслить”.
Томас Эдиcон
Прогресс цивилизации зависит от людей творческих, людей одарённых. Поэтому нам, педагогам, чтобы сохранить и развивать одарённость каждого ребенка в своей повседневной практической деятельности приходится быть очень внимательными к детям, их особенностям, способностям. Умение обучающегося объективно оценивать свои и чужие мысли, формулировать и аргументировать их, в процессе речи проверяя состоятельность, можно назвать критичностью ума. Это качество мышления развивает способность сопоставлять внешнюю информацию с имеющимися у подростка знаниями, вырабатывать решения о том, что использовать безусловно, что подвергать сомнению и проверять дополнительной информацией, а что и вовсе отвергнуть. Абстрактное (или критическое) мышление – это сплав умений действовать самостоятельно, активно, конструктивно. Сегодня учитель в современной школе - это высокопрофессиональный педагог, использующий в своей работе такие методы и приемы, которые помогут школьникам не только овладеть определенными знаниями, умениями и навыками в той или иной сфере деятельности, но и развивать их творческие способности. Одной из образовательных технологий, которая отвечает всем требованиям ФГОС, является технология развития критического мышления. Технология критического мышления предполагает равные партнерские отношения, как в плане общения, так и в плане конструирования знания, рождающегося в процессе обучения.
Цель мастер-класса: повысить мотивацию педагогов к применению технологии
критического мышления в образовательном процессе, познакомив с одним из приемов педагогической инновационной технологии «Кубик Блума»
Задачи мастер – класса:
-расширить понятие о критическом мышлении и методах развития критического мышления;
- показать приемы использования Кубика Блума в своей работе;
- научить слушателей использовать данный прием в своей практической деятельности.
Приведу примеры приемов, которые я наиболее часто использую в своей работе:
Приём "Верно — Не верно"
Прием "Верно — Не верно" удобнее всего применять в начале урока, когда идет повторение пройденного материала и подготовка учащихся к восприятию новой информации.
На этом этапе важно не только активизировать учащихся, подготовить, помочь им освежить в памяти все, что им известно по данной теме и те знания, умения и навыки, что пригодятся сегодня на уроке.
В то же время, с помощью вопросов и предположений ограничивается круг вопросов, которые будут обсуждаться на уроке. Учащиеся уже в начале занятия могут наглядно увидеть, что им предстоит узнать, что из этого они уже знали или предполагали, а что является неожиданным, что противоречит их знаниям.
Пример: «+» -верно, «-»- неверно
Учитель предлагает несколько утверждений по теме урока. Учащиеся фиксируют свои ответы, соглашаясь или отрицая услышанное. На стадии рефлексии необходимо вновь вернутся к этим вопросам и скорректировать свои ответы в связи с полученной информацией.
Тема «Вертикальные и смежные углы», «Признаки параллельности прямых», 7 класс
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.
2) Если угол равен 60°, то смежный с ним равен 120°.
3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.
4) Через любые три точки проходит не более одной прямой.
5) Вертикальные углы равны.
6) Если угол острый, то смежный с ним угол также является острым.
7) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.
8) Любые две прямые имеют не менее одной общей точки.
9) Через любую точку проходит более одной прямой.
10) Любые три прямые имеют не менее одной общей точки.
Лови ошибку
Учитель заранее подготавливает текст, содержащий ошибочную информацию, и предлагает учащимся выявить допущенные ошибки.
Важно, чтобы задание содержало в себе ошибки 2 уровней:
явные, которые достаточно легко выявляются учащимися, исходя из их личного опыта и знаний;
скрытые, которые можно установить, только изучив новый материал.
Учащиеся анализируют предложенный текст, пытаются выявить ошибки, аргументируют свои выводы. Затем изучают новый материал, после чего возвращаются к тексту и исправляют те ошибки, которые не удалось выявить в начале урока.
Пример:Два ученика решали уравнение 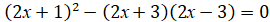 так:
так:
а)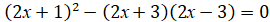
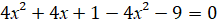
4х – 8 = 0
4х = 8
х = 2
Ответ: х = 2
б)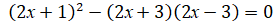
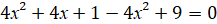
4х + 10 = 0
4х = - 10
х = - 2,5
Ответ: х = - 2,5
Найди верное решение. Исправь ошибку!
Прием «Сводная таблица»
Помогает систематизировать информацию, проводить параллели между явлениями, событиями или фактами. Выглядит эта таблица просто: Средняя колонка называется "линией сравнения". В ней перечислены те категории, по которым мы предполагаем сравнивать какие-то явления, события, факты. В колонки, расположенные по обе стороны от "линии сравнения", заносится информация, которую и предстоит сравнить.
Тема: «Тригонометрические функции», 10 класс
| Тема 1 | Тема 2 | Линия сравнения | Тема 3 | Тема 4 |
| y=sin x | y=cos x | область определения | y= tg x | y= ctg x |
|
|
| промежутки монотонности |
|
|
|
|
| четность, нечетность |
|
|
|
|
| нули функции |
|
|
|
|
| область значения |
|
|
Прием «Ромашка» «Ромашка» состоит из шести лепестков, каждый из которых содержит определённый тип вопроса:
Простые вопросы — вопросы, отвечая на которые, нужно назвать факты, воспроизвести определённую информацию.
Уточняющие вопросы — вопросы, целью которых является предоставление ученику возможностей для обратной связи относительно того, что он только что сказал.
Объясняющие вопросы — вопросы, направленные на установление причинно-следственных связей.
Творческие вопросы — вопросы, содержащие частицу «бы», элементы условности, предположения, прогноза.
Практические вопросы — вопросы, направленные на установление взаимосвязи между теорией и практикой.
Оценочные вопросы — вопросы, направленные на выяснение критериев оценки тех или иных событий, явлений, фактов.
"Признаки делимости на 2,5,10", 5 класс:
Простые вопросы: -Какие числа делятся на 2(5,10)?
Уточняющие: -Верно ли я тебя понял, что если число оканчивается цифрой 0, то оно делится на 5?
Объяснительные: - Почему сумма двух нечетных чисел является четным числом?
Практические: -Где используются признаки делимости?
Творческие: -Что было бы, если бы не были известны признаки делимости?
Оценочные:- Что тебе не понятно по данной теме?
Прием "Кубик Блума"
На этом приеме я бы хотела остановиться. Суть данного приема. Из плотной бумаги склеивается кубик. На каждой стороне пишется одно из следующих заданий: назови, почему, объясни, предложи, придумай, поделись.
Пример:
Тема «Прямоугольный параллелепипед», 5 класс
ПОЧЕМУ параллелепипед называют прямоугольным? (Потому что все грани прямоугольного параллелепипеда прямоугольники)
ОБЪЯСНИ что такое прямоугольный параллелепипед? ( это геометрическая фигура состоящий из 6 прямоугольников)
НАЗОВИ элементы прямоугольного параллелепипеда.(8 вершин, 6 граней, 12ребер)
ПРЕДЛОЖИ как из прямоугольного параллелепипеда получить куб? ( если все ребра прямоугольного параллелепипеда равны , то получится куб)
ПРИДУМАЙ рисунки с прямоугольным параллелепипедом.
ПОДЕЛИСЬ своими наблюдениями, где в жизни ты встречал предметы в форме параллелепипеда? (дома, мебель; электробытовые приборы)
Выводы: Методические приёмы технологии развития критического мышления способны обеспечивать высокие познавательные потребности одарённых обучающихся, формировать и развивать оригинальность, гибкость мышления и поддерживать устойчивый интерес к изучению математики.
Закончить свой мастер – класс мне хотелось бы словами Джона Холта:
«Учиться – значит задавать вопросы. Чтобы задавать вопросы, ребенку нужна вера в себя, а педагогу – умение ее поддержать»
Я хочу поблагодарить вас за работу и поддержку. Надеюсь, вам этот опыт пригодится в вашей деятельности.







 так:
так:












